岩土体边坡在降雨入渗作用下的稳定性及影响因素分析

2022-10-26吴旭敏叶志程

水资源与水工程学报 2022年5期

吴旭敏，杨溢，叶志程

(昆明理工大学公共安全与应急管理学院，云南昆明650032)

1 研究背景

从21世纪开始，相关数据表明滑坡是我国目前面临的主要地质问题之一[1]。由于降雨和雨水的入渗作用，使边坡受到冲刷和软化，从而导致了山体滑坡的发生[2]。近几年，全球气候变化导致了我国的特大暴雨频发。我国80%的地质灾难与降水有着密切的联系，而塌陷和滑坡事件占地质灾难的90%以上[3]，降雨入渗是导致边坡失稳的重要外在因素。郑开欢等[4]在考虑气象因素影响下对坡体的渗透作用进行了研究，指出在天然蒸腾作用下，降水对坡体稳定的作用存在着滞后效应；王进等[5]对降雨强度与浅层滑坡体入渗及稳定性的关系进行了研究，表明随着降雨强度的增大，边坡表面的入渗能力相应提高，同时加快了湿润锋的衰减运移速度；黄明奎等[6]通过研究极端降雨对边坡稳定性的影响，证明了在降水前期，极端降水对土壤的吸附量有显著的作用，且随入渗时间的延长而逐渐趋于平稳；陶志刚等[7]根据现场的实际施工状况，在不同降雨和堆载高度条件下对某排土场进行了模拟实验，研究了降雨作用对排土场边坡的影响；郑开欢等[8]在大雨环境下对分层碎石土的稳定特性进行了分析，指出在强降雨过程中分层砂土堆石场极易出现滑坡；蔡欣育等[9]研究得出了不同降雨类型的边坡失稳概率为前锋型和平均型，整体上大于中锋型和后锋型的结论；Koner等[10]以2D有限差分方法为基础，探讨了各种斜度下排土场的失稳机制；Rajak等[11]根据排土场的自然生态状况，分析了不同季节和强降水对排土场边坡面的作用；Zhu等[12]主要利用有限元法模拟了降雨入渗情况，并与实地钻探资料做对比，为前期降雨对边坡的影响研究奠定了基础。Mukhlisin等[13]通过有限元法模拟了前期降雨及不同降雨类型对边坡稳定的影响，提出雨强峰值对边坡稳定影响较大的观点。

目前，对降雨入渗作用下边坡稳定性进行的研究很多，但对降雨历时、降雨强度、主降雨类型、前期降雨综合考虑的研究相对较少。本文在众多学者研究的基础上分别就降雨历时、降雨强度、主降雨类型、前期降雨等方面进行多种工况的综合研究，采用GeoStudio软件的SLOPE/W模块对边坡降雨入渗时的稳定性进行模拟分析，并对边坡稳定性影响因素的敏感度进行对比分析。

2 模型建立

2.1 边坡几何尺寸

边坡选自某实际工程，该边坡从上到下分为4层，即人工填土、黏土、全风化玄武岩和坚硬玄武岩。模型边坡坡顶高度为48 m，坡底长度为79 m，坡顶、坡底宽度均为19 m。坡顶和坡底高差为20 m，边坡坡度为1∶2.05。

边坡模型及网格划分如图1所示。在模型分析中，表层的两层土是较为重要的，因此划分网格的大小设为0.5 m，全风化玄武岩的网格大小选择0.7 m，而最稳固的底层坚硬玄武岩网格大小选择1.0 m，所有网格形式均为四边形和三角形混合网格，共计6 829个节点，6 734个单元。

2.2 参数选取

2.2.1 边坡稳定性分析参数根据对该工程的现场调查勘测、室内试验结果以及相关规范，并参考以往边坡治理工程的经验值，确定的该工程岩土体主要参数值如表1所示。

2.2.2 降雨入渗参数本文在进行边坡的降雨渗流分析时，土壤水分特性曲线利用土体的饱和水含量和SEEP/W自带的粉质黏土等样本函数进行拟合，各岩土层的土壤水分特性曲线和渗透曲线相关参数如表2所示。

人工填土、黏土、全风化玄武岩的土壤水分特性曲线和渗透曲线如图2所示(坚硬玄武岩选用饱和模型，无上述曲线)。

调用MATLAB软件中的非线性拟合isqcurvefit函数，输入GeoStudio软件提供的土-水特性曲线的基质吸力和体积含水量进行VG(Van Genuchten)模型的拟合。

表1 边坡模型岩土体材料参数取值

表2 各岩土层的土壤水分特性曲线和渗透曲线相关参数

图2 边坡各岩土层的土壤水分特性曲线和渗透曲线

通过创建M-文件并输入Van Genuchten公式，在命令窗分别输入GeoStudio软件提供的土壤水分特性曲线的基质吸力和体积含水量，再为迭代计算赋值，指定体积水含量函数，利用函数拟合数据，获得VG模型的拟合参数[14]。设待定参数向量X=(θr,θs,a,n)，其中a、n为形状参数，计算出的人工填土、黏土、全风化玄武岩土层的参数向量分别为X=(0.0306，0.3357，0.0353，1.7550)、X=(0.0413，0.2998，0.0172，1.6075)、X=(0.0077，0.1996，0.1429，1.8582)。因而各岩土层的Van Genuchten拟合公式如下。

杂填土：

(1)

黏土：

(2)

全风化玄武岩：

(3)

式中：θ(h)为体积含水量[15]，m3/m3；h为基质吸力，kPa。

2.3 基本假定

降雨对边坡渗流的影响因素复杂多样。首先实际土体为不均质材料，不仅要受到前期降雨的影响，而且与排水状态等因素有关[16]。为突出研究重点和简化计算，分析时提出如下假设：各岩土层为均质材料，各向同性；不考虑全过程的水分蒸发；不考虑坡面积水，未能入渗的雨水均以地表径流的形式排出。

2.4 初始条件

为了研究降雨瞬态渗流对边坡孔隙水压力以及稳定性的影响，需要进行带有初始条件的稳态分析[17]。根据实际勘探钻孔资料，本文对模型坡顶侧设定地下水总水头为44 m，距坡顶5 m，设定模型坡脚侧总水头高度为22 m，距坡底7 m。边坡模型初始孔隙水压力及监测点设定如图3所示。

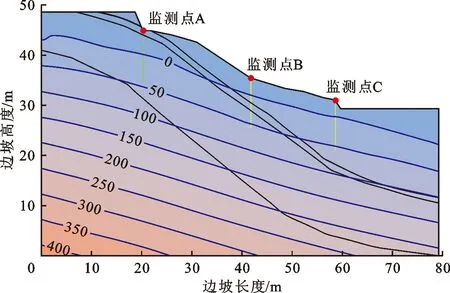
图3 边坡模型地下水压力及监测点设定(单位：kPa)

2.5 降雨方案选择

本文研究降雨入渗对边坡的影响，主要从降雨强度、降雨历时、主降雨类型、前期降雨4个因素引起边坡的孔隙水压力、稳定性及可靠度、应力应变3方面的变化进行论述。

降雨强度和降雨历时方面，根据我国降雨量划分标准：降雨量L<10 mm/d为小雨；降雨量10 mm/d≤L<25 mm/d为中雨，降雨量25 mm/d≤L<50 mm/d为大雨；降雨量50 mm/d≤L<80 mm/d为暴雨；80 mm/d≤L<120 mm/d 为大暴雨；降雨量L≥120 mm/d为特大暴雨[18]。依据本实际工程所在地的降雨监测记录，选取如表4所示的6组降雨方案。

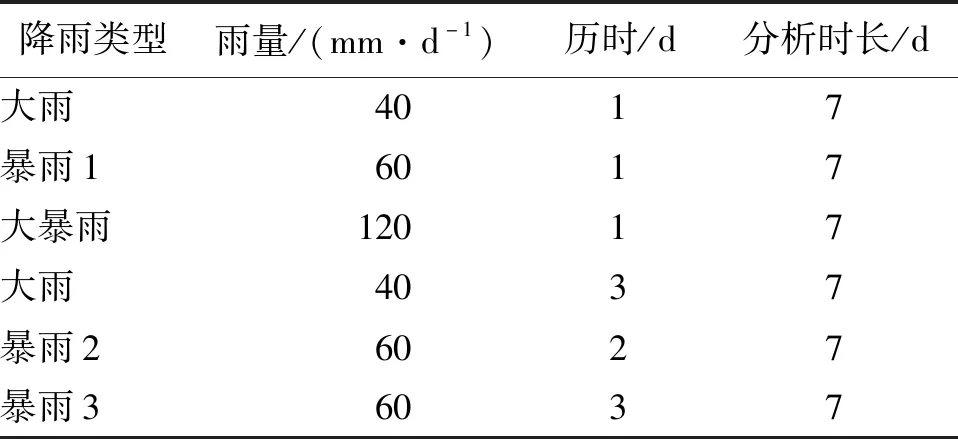
表4 边坡模型降雨方案选取

降雨类型方面，将主降雨与前期降雨分为平均型、前锋型、中锋型、后锋型4种类型。平均型：降雨天数内降雨强度不变；前锋型：降雨强度随时间逐渐减小；中锋型：降雨强度随时间逐渐增大，到达平均时长时降雨强度达到最大，后随时间逐渐降低；后锋型：降雨强度随时间逐渐增大[19]。根据工程当地降雨情况，总降雨量取0.3 m，降雨天数为5 d，考虑降雨后5 d，总分析时长为10 d。

3 结果与分析

3.1 降雨历时对边坡稳定性的影响

研究降雨持续时间对边坡稳定性的影响时，对边坡施加降雨强度为60 mm/d的降雨，分别施加1、2和3 d，降雨时间加上雨停后的时间总共7 d以研究边坡的一系列变化。

3.1.1 孔隙水压力变化图4、5分别为图3所示的坡顶监测点A和坡脚监测点C的孔隙水压力、体积含水量变化曲线。

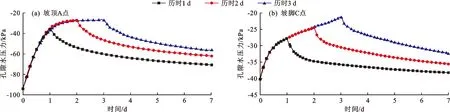
图4 降雨强度为60 mm/d不同历时边坡监测点孔隙水压力随时间变化曲线

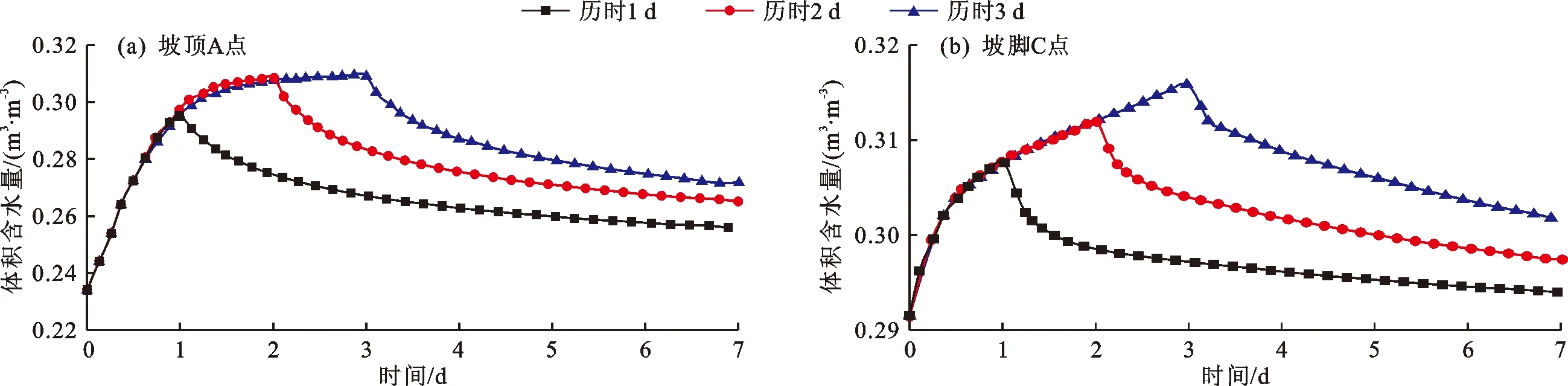
图5 降雨强度为60 mm/d不同历时边坡监测点体积含水量随时间变化曲线

由图4、5可以看出，边坡体积含水量变化曲线与孔隙水压力变化曲线变化趋势一致。同一节点在降雨强度相同的情况下，降雨历时越长，则体积含水量和孔隙水压力越大，雨停后，边坡体积含水量和孔隙水压力迅速下降。

3.1.2 边坡水平位移变化当降雨强度为60 mm/d时，不同降雨历时边坡水平位移随坡面高度变化曲线见图6。

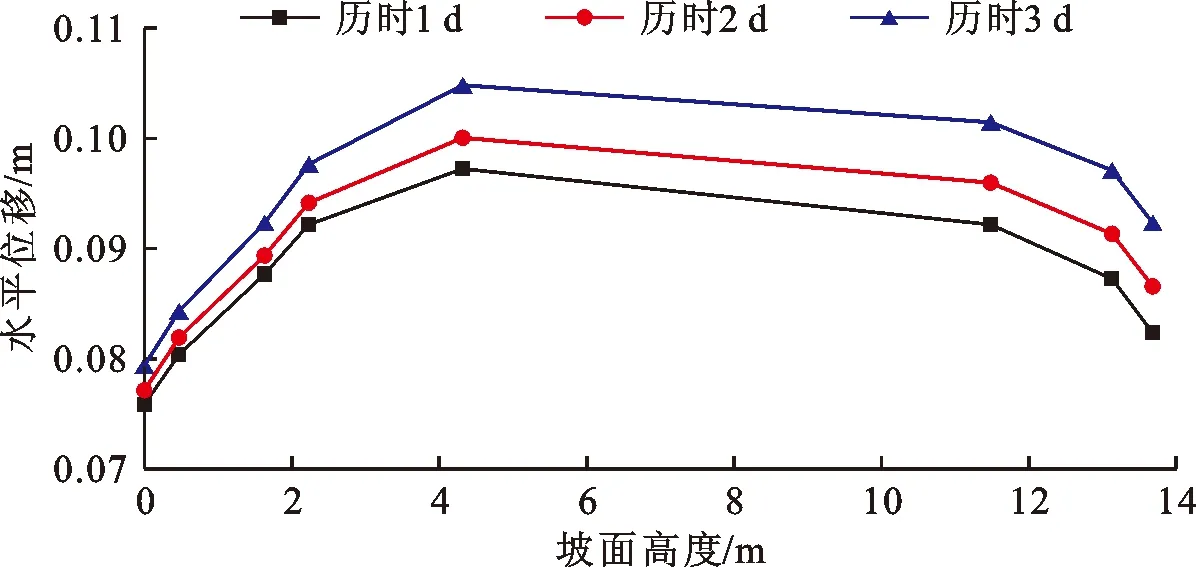
图6 不同历时边坡水平位移随坡面高度变化曲线(60 mm/d)

由图6可知，在持续降雨的情况下，边坡的水平位移值随降雨历时的增长而增大。降雨入渗作用使边坡内部体积含水量不断增大，边坡重度也随之增大，导致下滑力增大；同时伴随着基质吸力、内聚力和内摩擦角的减小，边坡体的抗剪强度和抗滑力也在减小。这些综合因素使边坡的水平位移随降雨历时的增长而不断增大。

3.1.3 边坡稳定性变化图7、8、9分别为在不同降雨历时或不同降雨强度的影响下，边坡的安全系数随时间变化曲线和地下水位线。

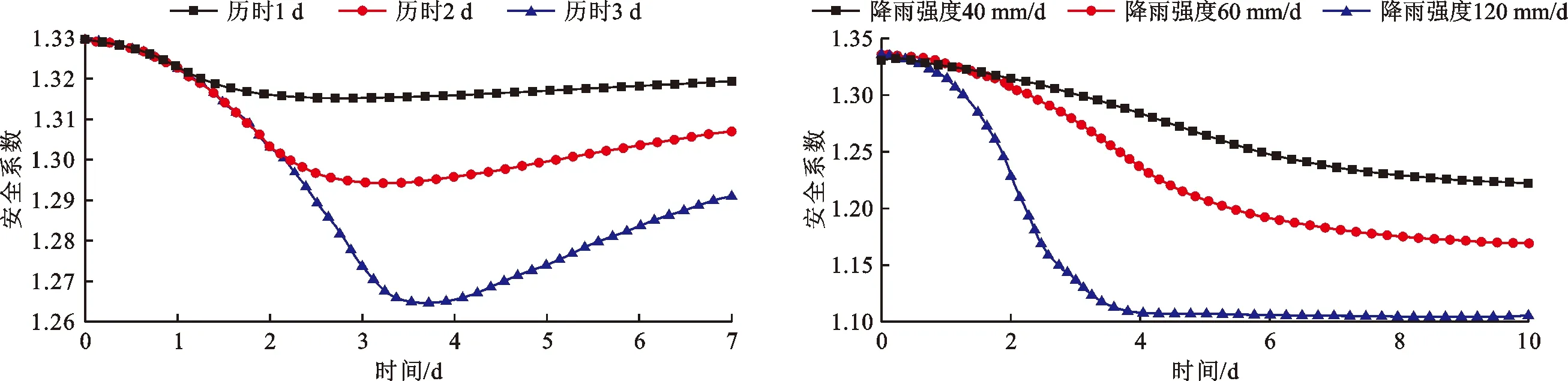
图7 相同降雨强度(60 mm/d)不同历时的边坡安全系数变化曲线图8 相同历时(10 d)不同降雨强度的边坡安全系数变化曲线

图9 不同降雨强度历时10 d的地下水位线

由图7可知，在降雨入渗的作用下，边坡的安全系数随降雨历时而不断降低直到雨停后一段时间，这是由于雨停后仍有一部分的雨水渗入边坡坡面，因此边坡的安全系数变化相较于降雨历时存在一定的滞后性。在雨停一段时间后，雨水不断下渗汇入地下水，边坡的孔隙水压力不断消散，抗剪强度增强，使其安全系数出现回升，但在以后的较长一段时间内仍然无法恢复到降雨前的状态，即降雨使边坡的安全系数在很长一段时间内出现一定幅度的下降，边坡的稳定会受到威胁。

由图8、9可知，无论降雨强度大小，边坡的安全系数在降雨初期会随着降雨历时而显著下降，但在一段时间后，边坡的安全系数变化逐渐平缓，最终趋于一个固定值。在长时间的雨水入渗作用下，边坡内岩土的体积含水量趋于饱和，渗水对边坡抗剪强度的影响达到一定的限度，所以边坡稳定性不再持续地减小而是趋近于一个固定值。而图8、9也说明降雨强度越大，相同降雨时间内雨水入渗量也就越大，地下水位也越来越高，岩土体也就越快达到饱和状态，这也是降雨强度越大相同降雨时间的边坡安全系数越小，且也越先出现安全系数趋于一个固定值的原因。

3.2 降雨强度对边坡稳定性的影响

3.2.1 降雨量相同降雨强度不同对边坡稳定性的影响在分析总降雨量相同的条件下不同降雨强度对边坡稳定性影响时，分别对降雨强度40 mm/d历时3 d、降雨强度60 mm/d历时2 d、降雨强度120 mm/d历时1 d的3种工况进行分析，该3种工况下边坡的安全系数随时间变化曲线及特征断面体积含水量随深度变化曲线如图10、11所示。

由图10可知，总降雨量一定时，降雨强度越大，对边坡的稳定性影响越大。在短时强降雨过程中，地表径流排出的雨量较大，入渗量要小于长时弱降雨过程，因此，短时强降雨结束后边坡的安全系数上升更快，而经长时弱降雨后，因边坡中雨水的渗入量大，其安全系数上升更缓慢。可见短时强降雨会造成边坡安全系数在短时间内剧烈下降，给边坡的稳定带来巨大威胁。由图11可知，短时强降雨对边坡表层土体的体积含水量影响更大，长时弱降雨则对边坡深层土体的体积含水量影响更大。

3.2.2 降雨时间相同降雨强度不同对边坡稳定性的影响在分析降雨时间相同的条件下不同降雨强度对边坡稳定的影响时，分别对历时1 d的降雨强度40、60和120 mm/d 3种工况进行分析。

(1)孔隙水压力变化。由图12可知，孔隙水压力随着降雨的持续而不断增大，且相同历时下雨量越大则孔隙水压力增长的幅度越大。在相同降雨量下坡面A、B、C 3个测点相比(图12(c))，坡顶A点孔隙水压力的变化幅度最大，其次是边坡中部B点，变化幅度最小的是坡脚C点。但由于坡脚离地下水位更近，初始孔隙水压力较大，所以可以推测坡脚的孔隙水压力先达到零值，即刚好饱和。以降雨强度60 mm/d为例，坡顶A点孔隙水压力的增幅为57 kPa，边坡中部B点增幅为18 kPa，坡脚C点增幅为12 kPa。雨停后，之前降雨量越大，则各监测点孔隙水压力的减小幅度也越大；相同降雨量下(图12(c))，坡顶A点孔隙水压力的减小幅度最大，边坡中部B点次之，坡脚C点最小，这是由于降雨结束后边坡坡脚的体积含水量下降幅度相对较小，使得该处孔隙水压力的减幅也相对较小，以降雨强度60 mm/d为例，坡顶A点的孔隙水压力减小幅度为33.0 kPa，边坡中部B点为15.6 kPa，坡脚C点为10.4 kPa。总体而言，降雨强度越大，则边坡孔隙水压力越大、基质吸力越小、渗透系数越大，相同时间内，就有越多的雨水渗入边坡。

(2) 边坡水平位移变化。历时1 d的不同降雨强度下，边坡水平总位移等值线分布见图13，边坡安全系数随时间变化曲线见图14。

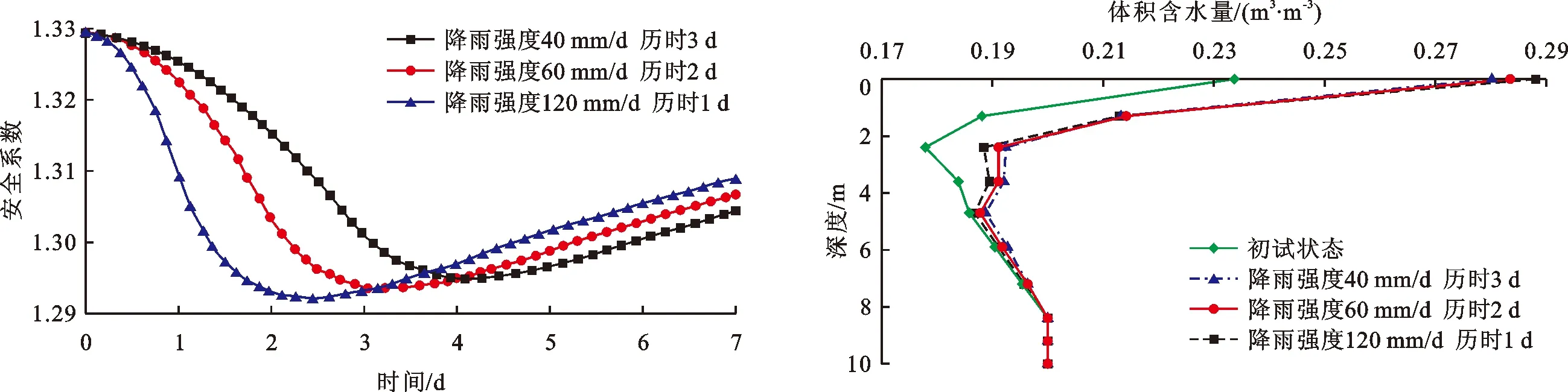
图10 不同降雨条件下边坡安全系数随时间变化曲线图11 不同降雨条件下边坡体积含水量随深度变化曲线

图12 历时1 d的不同降雨强度下边坡A、B、C监测点孔隙水压力变化曲线

图13 历时1 d的不同降雨强度下边坡水平总位移等值线分布(单位：m)

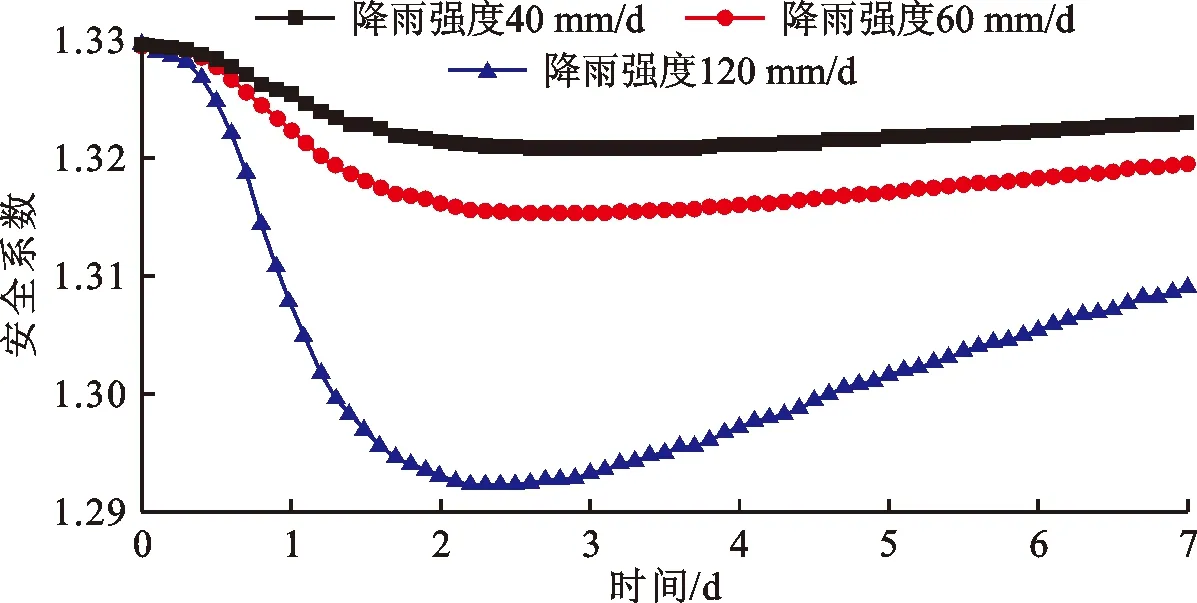
图14 历时1 d的不同降雨强度下边坡安全系数随时间变化曲线

由图13可知，当降雨历时相同时，不同降雨强度作用下，边坡水平位移的范围和数值均随着降雨强度的增大而增大，且水平位移最大值主要集中在边坡坡面的中上位置；坡面位移朝向边坡右下方，坡底位移主要朝正下方。由图14可知，在降雨历时相同的条件下，边坡安全系数随着降雨强度的增大而减小。

3.3 主降雨类型对边坡稳定性的影响

对边坡施加后锋型、平均型、前锋型、中锋型4种降雨类型，各类型降雨历时5 d，雨停后继续观察5 d，分析10 d内边坡的一系列变化。

3.3.1 边坡的体积含水量变化图15为边坡受不同降雨类型时，坡顶A点、坡脚C点的孔隙水压力随时间变化曲线。

由图15可知，不同雨型各测点的孔隙水压力峰值大小顺序均为后锋型>中锋型>平均型>前锋型，且变化趋势相似。降雨初期，前锋型降雨的孔隙水压力迅速上升，中锋型和平均型降雨的上升速度相近，后锋型降雨上升速度最慢；降雨中期，由于前锋型降雨的强度减弱，使孔隙水压力开始下降，而中锋型降雨的孔隙水压力在此阶段达到最大；降雨后期，后锋型降雨的孔隙水压力达到最大，其次是平均型降雨。雨停后，各类型降雨的孔隙水压力迅速减小并逐渐趋近于相同值。

3.3.2 边坡稳定性变化图16为不同降雨类型下边坡的安全系数随时间变化曲线。

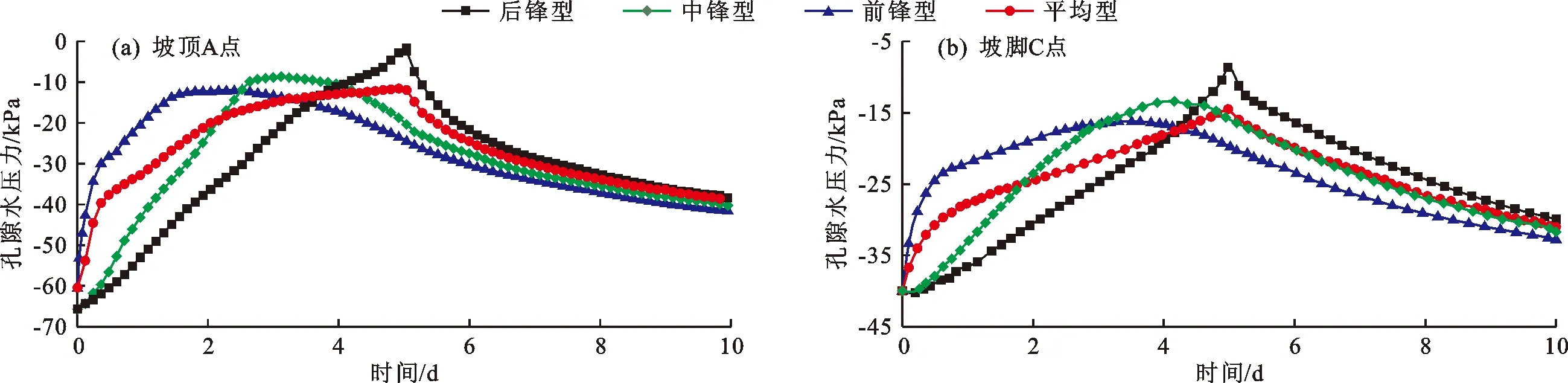
图15 不同降雨类型边坡监测点孔隙水压力随时间变化曲线

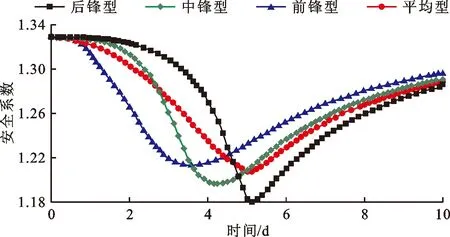
图16 不同降雨类型边坡安全系数随时间变化曲线

由图16可以看出，降雨初期，前锋型降雨的边坡安全系数在达到最小值之前，其减小幅度在4种降雨类型中最大，后锋型降雨最小，平均型和中锋型降雨相似，该规律持续至第3.625 d。第3.625～4.750 d，由于前锋型降雨强度的减弱，其边坡安全系数首先出现回升，中锋型降雨的边坡安全系数在此阶段达到最小值并于第4 d开始回升。第4.750 d之后，后锋型降雨的边坡安全系数逐渐达到最小值，并与平均型降雨的安全系数在雨停后出现回升。雨停后，随着雨水的不断下渗，4种降雨类型下的边坡安全系数持续回升，并逐渐趋近于相同的值。虽然每种降雨类型的降雨总量和降雨时间相同，但边坡安全系数最小值及其出现的时间各不相同，雨停后边坡安全系数的大小按雨型排序为前锋型>中锋型>平均型>后锋型，后锋型降雨的边坡安全系数在第4.750 d之后始终最小，因此在实际工程中应重视后锋型降雨对边坡稳定的影响。

3.3.3 边坡水平位移变化图17给出了不同降雨历时的各种降雨类型下，边坡水平位移随坡面高度的变化曲线。

由图17可知，降雨初期，前锋型降雨对边坡位移的影响显著，边坡在各种类型降雨作用下的水平位移大小顺序为前锋型>平均型>中锋型>后锋型；降雨中后期，中锋型降雨成为对边坡水平位移影响最大的降雨类型，水平位移大小顺序变为中锋型>前锋型>平均型>后锋型；降雨后期，水平位移大小顺序则变为后锋型>平均型>中锋型>前锋型。降雨类型对边坡水平位移的影响与对边坡安全系数的影响规律相符合。

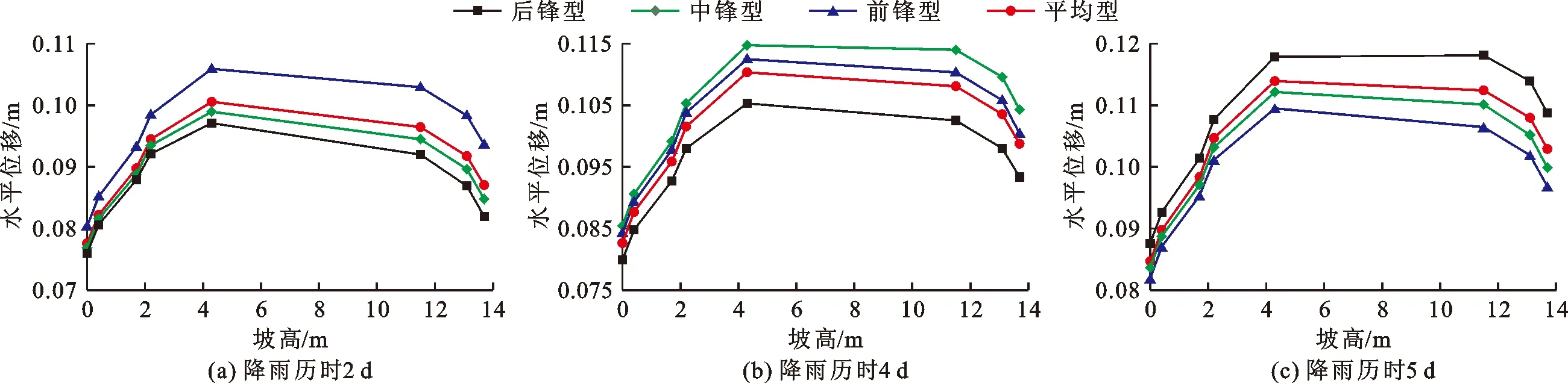
图17 不同降雨历时各降雨类型边坡水平位移随坡面高度变化曲线

3.4 前期降雨对边坡稳定性的影响

3.4.1 前期降雨强度的影响对边坡施加前期降雨，降雨强度分别为40、60、100和160 mm/d，历时5 d，然后在第6 d施加降雨强度为120 mm/d的主降雨，前期降雨和主降雨过程中边坡安全系数变化曲线如图18所示。由图18可知，主降雨后边坡安全系数随前期降雨强度的增大而减小。

3.4.2 前期降雨类型的影响对边坡分别施加后锋型、中锋型、前锋型和平均型的前期降雨，历时5 d，总降雨量均为300 mm，然后在第6 d施加降雨强度为120 mm/d的主降雨。前期降雨不同雨型+主降雨的降雨强度过程线见图19，各降雨过程作用下边坡的安全系数变化曲线见图20。

图18 不同降雨强度的前期降雨+主降雨作用下边坡安全系数变化曲线

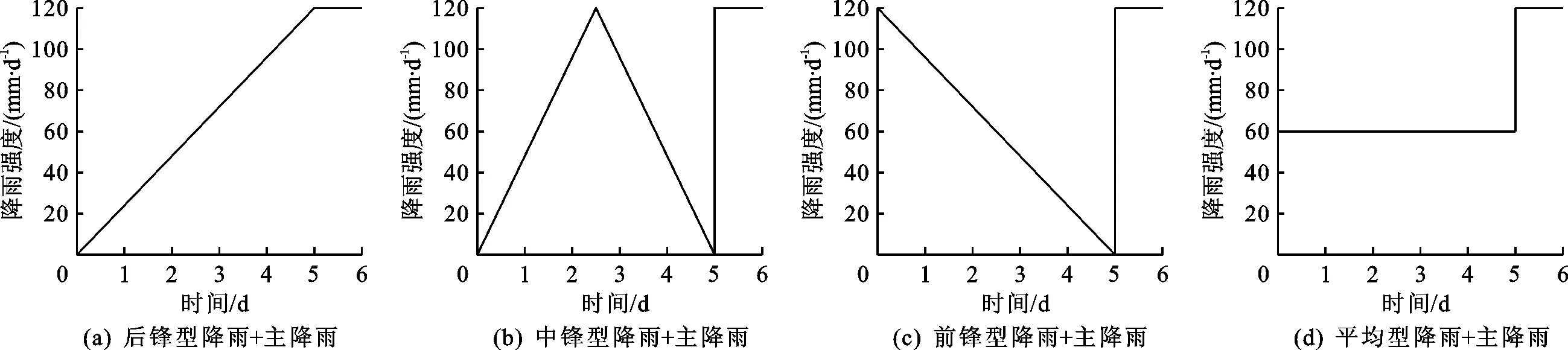
图19 前期降雨不同雨型+主降雨的降雨强度施加过程线

图20 前期降雨不同雨型+主降雨作用下边坡安全系数变化曲线

由图20可知，在前期降雨过程中的第3.5 d之前，前锋型降雨的边坡安全系数最小；第3.5 d ～第5 d之间，中锋型降雨的边坡安全系数最小；后锋型降雨的边坡安全系数基本在整个前期降雨过程中为最大。在施加主降雨后边坡安全系数持续减小，前期降雨不同雨型相应的边坡安全系数大小顺序为前锋型>中锋型>平均型>后锋型。

3.4.3 前期降雨与主降雨不同间隔时间的影响图21为对边坡施加降雨强度为60 mm/d的前期降雨5 d后，分别间隔0、1、2、3、4和5 d再对边坡施加降雨强度为120 mm/d的主降雨1 d时边坡的安全系数变化曲线。

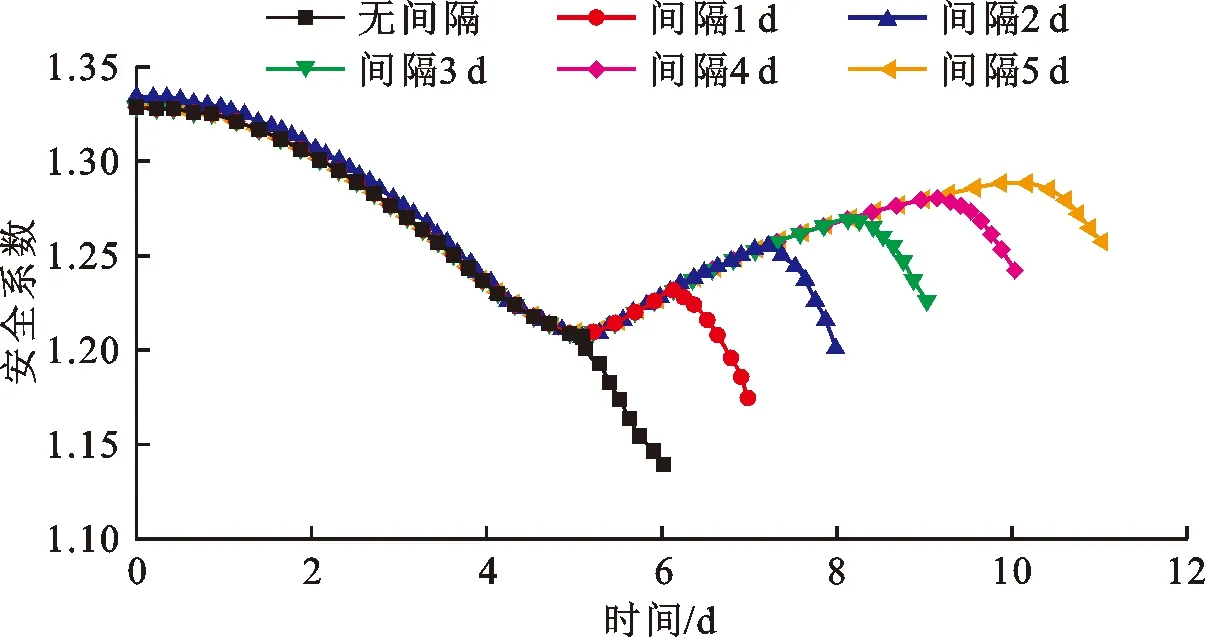
图21 前期降雨+不同间隔时间主降雨作用下边坡安全系数变化曲线

由图21可知，无时间间隔施加主降雨时，边坡的安全性最差，间隔越长则主降雨期边坡的安全系数越大。这是由于边坡内的水在无降雨间隔期会不断下渗，边坡岩土的抗剪强度随之逐渐上升，安全系数也逐渐增大，因而间隔时间越长，在施加主降雨后的边坡安全系数越大。另外随着间隔时间的增大，施加主降雨后的边坡安全系数下降幅度减小，这是由于间隔时间越长，则边坡内的体积含水量越低，渗流速度越小，相同一段时间内入渗坡体的水量越少，因而边坡安全系数降低的幅度越小。

4 敏感性分析

在一定的外部环境下，影响边坡稳定性的边坡岩土参数主要有重度、黏聚力以及内摩擦角，为了比较这些参数对边坡稳定性的影响程度，利用GeoStudio SLOPE/W自带的单因素分析法，分析边坡安全系数在各岩土层参数变化下的敏感性，即各岩土层参数变化对边坡安全系数的影响程度[20]。边坡安全系数K可看作各个影响因素xn的函数，其表达式如下：

K=f(x1,x2,…,xn)

(4)

通过对安全系数的相对变化与单因素的相对变化的比值En进行比较，来分析各因素对安全系数的影响程度，En计算公式如下：

(5)

本次敏感性分析主要以边坡杂填土、黏土、全风化玄武岩3个岩土层的重度、黏聚力和内摩擦角为影响参数，各参数设定为均匀分布，敏感性步数均为10。各影响参数取值如表5所示。

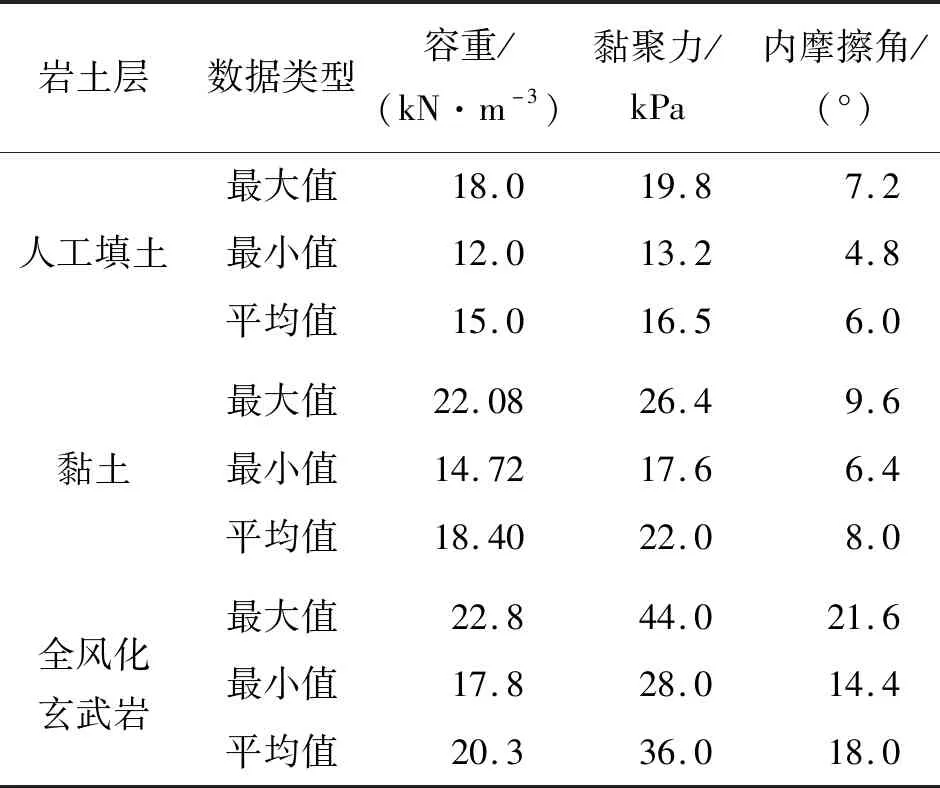
表5 敏感性分析各岩土层主要影响参数取值

根据上述3个岩土层各主要参数的相对变化率对边坡安全系数的影响计算得到其敏感度范围，并绘制出不同岩土层各参数的安全系数-敏感度范围图，如图22所示。

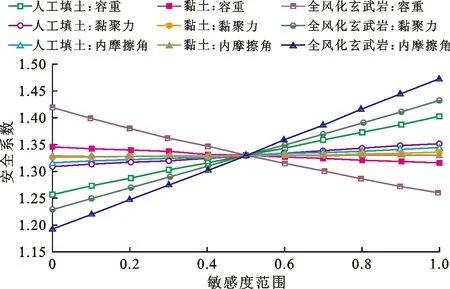
图22 不同岩土层主要参数对边坡安全系数影响的敏感性范围

由图22可知，各岩土层参数对边坡安全系数的影响程度不尽相同。黏土和全风化玄武岩的容重与边坡稳定性成负相关，即岩土层的容重越大，则边坡的稳定性越小；人工填土的容重以及全风化玄武岩的黏聚力和内摩擦角与边坡的稳定性呈正相关，即这些参数越大，则边坡越稳定；人工填土和黏土的黏聚力和内摩擦角变化对边坡的稳定影响较小。

5 讨论

大量的工程实践证明，降雨入渗会影响边坡的稳定性。根据付宏渊等[21]的研究，随着降雨历时的增长，边坡容易发生局部分层垮塌或整体滑移。在降雨停止后，岩质边坡稳定性的持续降低有所延缓，本文研究结果也符合此规律。在降雨入渗的作用下，边坡的安全系数随之不断减小直到雨停后一段时间，这是由于雨停后仍有部分雨水渗入边坡，因此边坡的安全系数变化相较于降雨历时存在一定的滞后性。在雨停一段时间后，雨水不断下渗流入地下水，孔隙水压力不断消散，抗剪强度增强，使得安全系数出现回升，但在雨后较长的时间内仍然无法恢复到降雨以前的状态，安全系数在长时间内会出现一定幅度的下降，对边坡的安全产生威胁。

目前，国内外关于降雨入渗作用下边坡稳定性的研究成果较多，但对降雨历时、降雨强度、主降雨类型、前期降雨综合考虑的研究相对较少。本文在众多学者研究的基础上进行了综合分析，分别就降雨历时、降雨强度、主降雨类型、前期降雨等因素对边坡降雨入渗稳定性的影响进行模拟分析，同时对影响边坡稳定性的主要参数的敏感度进行了对比分析。本研究较全面地考虑了降雨入渗影响边坡稳定性的各种因素，从一定程度上克服了该方面传统分析结果精确性不足的缺陷。当然，在实际操作过程中，也需要对工程现场进行详细勘测和深入调查，以期能获得更符合工程实际情况的分析结果。