基于LSTM神经网络模型的液压管路故障诊断方法*

2022-10-26孟秋静

机电工程 2022年10期

关键词：凹坑端部管路

孟秋静,杨钢

（1.上海电子信息职业技术学院中德工程学院,上海 201411;2.重庆交通大学机电与车辆工程学院,重庆 400074）

0 引言

航空发动机外部液压管路系统如同“心血管”,为发动机输送介质。管路是否发生故障将对发动机安全性和可靠性有至关重要的影响[1-3]。

据有关部门统计,在飞机液压系统管路故障中,民航领域相关故障占其总故障的36.7%[4],因此,开展航空发动机液压管路振动失效机理研究,准确地识别出液压管路裂纹、磨损和凹坑等典型故障,具有重大意义。

近年来,部分学者对航空发动机管路系统的振动特性进行了研究。例如,李哲洙等人[5]提出了一种基于黄变换的航空液压管路裂纹故障诊断方法。ANTON B等人[6]研究了液压管路流固耦合振动特性,进而对管路振动故障进行了研究。ZHU H Z等人[7]研究了液压管路的动态特性,并分别应用动刚度法对其进行了分析。窦金鑫等人[8]研究了含裂纹航空液压直管的振动响应特性,利用Newmark-β积分法求解了液压直管的振动响应。

上述文献对液压管路的故障进行了研究,并取得了一定的成果,但是基于数据驱动的航空发动机液压管路典型故障诊断方法的研究几乎还是空白的。

长短期记忆（LSTM）网络是由循环神经网络衍生而来的时序卷积神经网络[9],具备一定的长距离时序数据的信息挖掘能力。基于LSTM,FAN C等人[10]在语音识别、机器翻译和负荷预测等领域的研究取得了一定的成果。樊家伟等人[11]提出了一种基于LSTM神经网络和故障特征增强的行星齿轮箱故障智能诊断方法,利用LSTM神经网络模型对故障特征进行了智能提取。罗嗣棂等人[12]研究了基于LSTM的健康状态评估分析方法。

上述研究虽然取得了一定的成果,但是未利用实测的振动数据加入高斯噪声,验证模型的鲁棒性。

由于航空液压管路结构复杂多样,导致液压管路的故障机理比较复杂,很难准确地发现液压管路的故障特征。因此,笔者基于LSTM原理建立端到端的航空液压管路故障识别模型。

首先,笔者通过对液压管路实测的振动数据进行训练的方式,实现数据特征融合的目的;然后在实测数据加入高斯噪声,就模型对强噪声信号的鲁棒性进行验证;最后,针对航空液压管路所涉数据的复杂性,尝试建立能够同时融合液压管路数据局部特征和全局特征的模型,作为进一步深入研究的重点。

1 基本理论

1.1 时间信息提取

作为一种在循环神经网络基础上的新生算法,LSTM可以有效地解决RNN中出现的梯度消失与爆炸问题[13]。LSTM神经网络与RNN拥有同样的自循环反馈的全连接神经网络结构,但是RNN的网络结构是相对比较简单的细胞结构。而LSTM神经网络在神经元中增加了遗忘门、输入门和输出门等3个独特的“门”结构,使状态信息可以被添加和筛除。

LSTM基本细胞结构如图1所示。

LSTM神经网络模型的训练过程为:

ft=σ（Wf·[ht-1,xt-1]+bf）

（1）

it=σ（Wi·[ht-1,xt-1]+bi）

（2）

Ct=ft⊙Ct-1+it⊙tanh（WC·[ht-1,xt-1]+bC）

（3）

ht=σ（Wo[ht-1,xt-1]+bo）⊙tanh（Ct）

（4）

式中:it—输入门；ft—遗忘门；Ot—输出门；ht—t时刻传递给下一个时刻的短时记忆状态，同时也是t时刻的输出；ct—细胞的长时状态，即LSTM神经网络的长时记忆。

1.2 模型设计及参数

基于LSTM神经网络原理,并结合航空液压管路振动信号的特点,笔者对长短期记忆神经网络模型进行了优化,建立了具有学习一维时间序列的LSTM模型。该模型主要包括输入层、展开层、2个LSTM层、全连接层和输出层等5部分。

首先,笔者将一维液压管路振动信号输入到LSTM模型中;然后,利用模型中的LSTM层对管路数据进行特征学习,将提取到的特征被映射到样本标记空间（模型选用ReLU函数作为激活函数，此处,全连接层对时域信号的特征分类是关键的一步,主要是通过其对管路特征进行加权计算实现特征空间转换[14,15]）;最后,通过SoftMax层进行分类诊断,利用适量的样本数据和ADAM优化算法,对模型中重要的参数W、b进行多次迭代更新,从而使得模型具有较好的诊断能力。

LSTM模型的主要参数如表1所示。

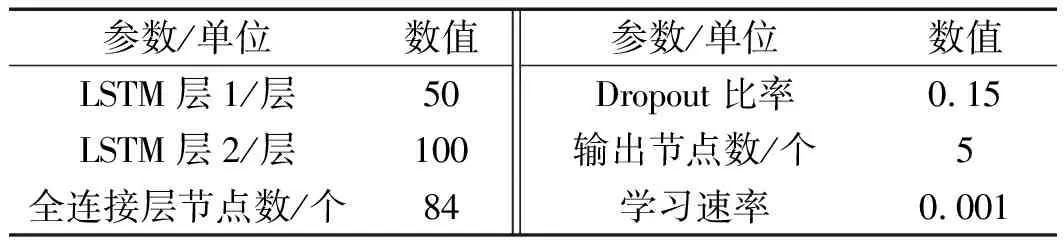
表1 LSTM模型主要参数

2 航空发动机管路故障诊断模型

航空发动机液压管路系统结构复杂,同时液压管路受流固耦合振动特性及外界强大噪声干扰等因素影响,导致液压管路的振动信号呈现强大的非线性和非平稳性。

为了充分发挥LSTM模型针对振动信号全局特征的优势,实现时间信息融合目的,笔者提出了LSTM航空液压管路故障诊断模型。该模型在一定程度上综合了全局特征,从而可以应用于液压管路健康状态、不同故障类型和不同故障位置的诊断识别中。

液压管路故障诊断的具体流程图如图2所示。

（1）管路信号采集。利用传感器对每一类工况下的航空液压管路进行振动信号的拾取,2个传感器分别拾取布置在管路端部和管路中间等两个测点位置;

（2）数据集创建。将采集的振动信号创建成航空液压管路数据集;并将数据集划分为数据集A和数据集B,其中,数据集A主要是由航空液压管路的原始振动信号组成,数据集B主要是由航空液压管路的原始振动信号加随机噪声信号组成;

（3）LSTM模型设计。按照LSTM模型的设计原则以及结合航空液压管路振动数据的特点进行设计;并将管路数据的训练集输入到所设计的模型中,进行参数调试与训练,从而获得稳定的LSTM模型;

（4）鲁棒性验证。将数据集B输入到设计的模型中,从而有效地验证该模型的鲁棒性;

（5）管路智能诊断。利用测试集验证基于LSTM模型的液压管路故障诊断模型的有效性;并基于同一数据集,与RNN、CNN、SVM和BPNN模型的训练结果进行对比分析。

3 实验与分析

3.1 实验说明

为了验证模型的有效性,笔者利用航空液压管路实验台对管路数据进行采集。

首先，笔者对液压管路进行故障植入;其次，将故障实验件在航空液压管路模拟实验台上进行固定;最后，利用振动信号采集仪进行数据采集。

实验的基本设置参数如表2所示。

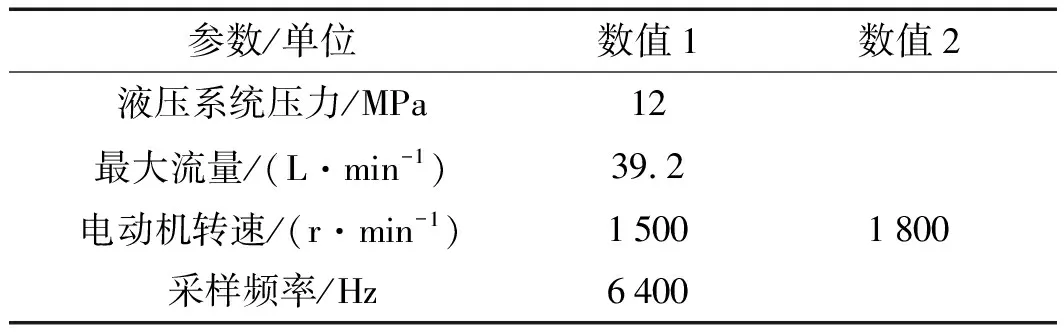
表2 实验基本参数表

航空液压弯管振动信号实验测试图如图3所示。

由图3可以看出:该实验主要是由2个加速度传感器同步进行航空液压管路振动信号拾取。

该实验分别选取管路中间位置为测点1,管路端部位置为测点2,管路两端由块状卡箍约束固定。

由表2可以看出:实验选用的液压系统压力为12 MPa,管路内部的最大流量为39.2 L/min;设定2个参数,即电动机转速分别为1 500 r/min和1 800 r/min等;振动数据采集仪的采样频率选用4 096 Hz,且符合香农采样定理。

3.2 数据说明

为验证模型在大量噪声环境下的鲁棒性,笔者依据航空发动机在实际工作中的状态,在测试集B信号中加入20 dB的高斯白噪声,以模拟实际工程中液压管路的工作状态[16];另外,将测试集B输入到LSTM模型中。

染噪后,笔者选取测点1采集的液压弯管管路健康振动信号的时域波形图,如图4所示。

由图4可以发现：染噪前,当液压管路状态健康时,航空液压管路振动信号的幅度均较小,时域波形较规律,幅值大小为0.2 g左右。

染噪后,笔者选取测点1采集的管路裂纹故障信号的时域波形图,如图5所示。

由图5可以发现:当航空液压管路在不同位置出现裂纹或者凹坑故障时,振动信号的幅度将明显增大,幅值大小在0.4 g以上,该幅值为液压管路健康状态时的2～3倍,振动信号的幅值和时域波形均有类似变化;染噪声后,液压管路振动信号的幅度增大,幅度增加1倍左右,且时域波形发生较大变化。

由于航空液压管路在实际工程中振动信号受强大噪声干扰,因此,仅通过振动信号的时域波形很难准确地识别出航空液压管路裂纹和凹坑等管路典型故障。

染噪后,笔者选取测点1采集的管路凹坑故障信号的时域波形图,如图6所示。

由图6可以发现:当管路凹坑故障时,振动信号的时域波形图与管路裂纹故障时的振动信号的时域波形图类似,幅值大小均在0.4 g以上;且染噪声后,时域波形发生较大变化,幅度增至未染噪时的两倍。

3.3 数据集创建

为避免故障信息遗漏,笔者将数据堆叠成一个通道样本,其中,每段样本信号包含3 570个数据点;基于样本信号创建数据集,其中,训练集为2 313个样本,测试集A为356个样本,测试集B为1 071个样本。训练样本数量和预测样本数量的比例为8 ∶2。

基于同一数据集,笔者利用LSTM与RNN、CNN、BPNN和SVM等5种故障诊断模型[17],对液压管路故障诊断进行对比分析。

液压管路训练迭代次数与损失值曲线如图7所示。

由图7可看出:基于优化LSTM模型的训练样本损失值,随着迭代次数的增加而不断减小,并在迭代2轮以后基本趋近于零,该模型达到收敛条件,说明训练效果较理想,实际输出能很好地逼近理论输出;

而由于强噪声干扰,CNN模型训练前期损失值波动较大,当迭代4轮以后,CNN模型基本达到收敛条件,但是迭代到14轮以后模型陷入了局部收敛,说明CNN模型的泛化性能较差;

而RNN模型当迭代次数达到20轮以后,仍有波动的训练误差,损失值还不能趋近于零,说明RNN网络模型训练收敛性较差且稳定性不高。

3.4 可视化及分析

为了进一步展示LSTM模型对于航空液压管路不同故障类型特征的学习能力,笔者利用t-SNE（t-distributed stochastic neighbor embedding）降维算法进行特征可视化。

其中,LSTM模型全连接层样本分类结果如图8所示。

由图8可看出:在航空液压管路振动样本数据中,基于LSTM模型能够清晰地区分出液压管路系统中健康状态和4类故障状态;不同类型的液压管路故障数据具有鲜明的分簇,未发现交叉重叠的部分。

由此可以说明,其聚类效果十分明显,基本上达到理想的聚类效果。

CNN模型全连接层样本分类结果如图9所示。

由图9可以看出:由于噪声及干扰信号的影响,基于CNN模型能够大致区分出5类液压管路故障数据,其中,液压管路健康状态、液压管路中间裂纹和液压管路端部凹坑等3种数据能够形成自己的分簇,而簇内的聚集度相对较差;同时,液压管路端部裂纹和液压管路中间凹坑等2类故障的分簇出现严重的交叉现象,两簇数据点的距离相对比较近。

RNN模型全连接层样本分类结果如图10所示。

由图10可以看出:基于RNN模型可以比较清晰地将液压管路健康状态区分出来;其他4种液压管路状态分簇不明显,聚集度十分分散,出现严重的数据交叉重叠现象,说明CNN和RNN模型的聚类效果相对较差。

3.5 结果及评估

为验证LSTM模型对航空液压管路故障分类的可行性和有效性,笔者分别采用准确率（Accuracy）、精确率（Precision）、召回率（Recall）和F1-sore等4个评价指标,用于评价该模型的分类性能[18,19]。

混淆矩阵是深度学习中一种常见的可视化工具,能够更全面地反映每种故障状态的识别情况。在同一数据集中,利用所建的LSTM故障诊断模型对航空液压管路数据进行训练,得到的混淆矩阵如图11所示。

对于液压管路数据标签描述如表3所示。

表3 液压管路数据标签的描述

由图11（a）可以看出:当数据集中加入噪声前,LSTM模型对航空发动机液压管路故障的总体识别率为99.9%,准确率较高,仅有0.1%的管路端部裂纹故障数据被错误地识别为中间凹坑故障,从而导致总体出现0.1%的错误率;而当数据集中加入噪声后,受噪声干扰,LSTM模型对航空发动机液压管路故障的总体识别率为99.1%,由于深度学习强大的结构优势,LSTM模型中遗忘门会将不重要的部分数据进行遗忘和筛除,从而保证LSTM模型对航空液压管路的识别准确率不至于明显下降,在总体准确率上仅降低0.8%;

数据集中加入噪声后,由图11（b）可以看出:LSTM模型对于航空液压管路健康状态、液压管路端部凹坑和液压管路中间凹坑等单一故障识别的精确率均为100%;而对于端部裂纹故障的识别,有0.2%的样本数据被错误地识别为中间凹坑故障;对于中间裂纹故障,则有0.7%的样本数据被错误地识别为端部凹坑故障,从而导致端部凹坑故障的错误率最高,达到3.5%,这也导致了LSTM模型总体出现99.1%的识别率。

利用CNN模型的故障诊断方法训练得到的混淆矩阵,如图12所示。

由图12（a）可以看出:当数据集中加入噪声前,CNN模型对航空发动机液压管路故障的总体识别率达到96.2%以上,准确率较高;对于航空发动机液压管路健康状态、液压管路端部凹坑和液压管路中间凹坑等单一故障的识别率均达到100%;而对于液压管路端部裂纹故障的识别,有0.5%的样本数据被错误地识别为液压管路中间凹坑故障;对于液压管路中间裂纹故障,出现3.3%的样本数据被错误地识别为液压管路端部凹坑故障,从而导致端部凹坑故障的召回率最高,达到15.8%;

由图12（b）可以看出:当数据集中加入噪声后,受强大的噪声干扰,导致CNN模型的准确率出现大幅度下降的现象,相比加入噪声前的总体准确率降低12.8%;而CNN模型对于液压管路健康状态、液压管路端部裂纹和液压管路中间裂纹等单一故障识别的精确率均为100%;对于液压管路端部凹坑故障的识别,有0.1%的样本数据被错误地识别为液压管路中间裂纹故障;对于液压管路中间凹坑故障的识别,则出现了16.5%的样本数据被错误地识别为液压管路端部裂纹故障,从而导致液压管路端部裂纹故障的错误率最高,达到46.4%,同时也导致了CNN模型出现了16.6%的错误率。

这说明CNN模型稳定性不高。

笔者利用RNN模型的故障诊断方法训练得到的混淆矩阵,如图13所示。

由图13（a）可以看出:当数据集中加入噪声前,RNN模型对液压管路故障的总体识别率达到91.5%以上,对于管路健康状态、管路中间裂纹和管路端部凹坑等单一故障的识别率均达到100%;而RNN模型对于管路端部裂纹故障的识别,存在0.1%的样本数据被错误地识别为管路中间凹坑故障;对于管路中间凹坑故障的识别,出现8.3%的样本数据被错误地识别为管路端部裂纹故障,从而导致管路端部裂纹故障的错误率最高,达到31.3%;

由图13（b）可以看出:当数据集中加入噪声后,导致RNN模型的准确率出现大幅度下降的现象,相比加入噪声前,识别总体准确率降低11.1%,而对于液压管路健康、管路中间裂纹和管路中间凹坑等单一故障识别的精确率均为100%;RNN模型对于管路端部凹坑故障的识别,有1.9%的样本数据被错误地识别为管路中间裂纹故障;对于管路端部裂纹故障的识别,则有17.7%的样本数据被错误地识别为管路中间凹坑故障,导致了管路中间凹坑故障的错误率最高,达到46.8%的错误率。

基于同一数据集加入噪声前利用LSTM模型与其他4种方法的训练结果,笔者作了进一步对比分析。为了避免偶然性误差,笔者对每种方法各进行了10次试验,将各类评估指标的平均值作为该方法的分类诊断性能评估指标。

染噪声前,笔者利用LSTM方法与其他4种方法的4个评价指标,如表4所示。

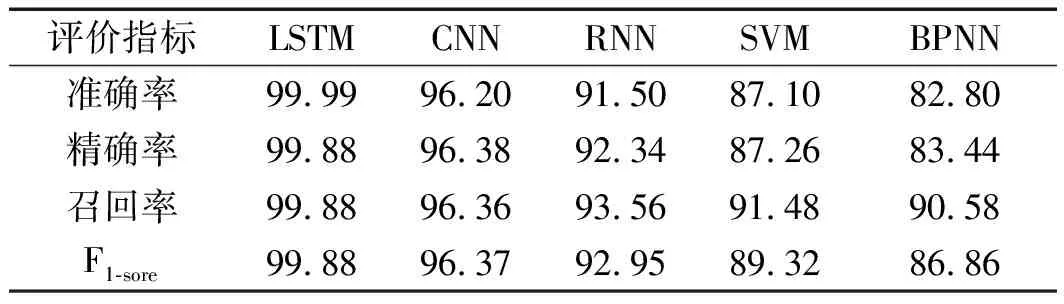
表4 染噪声前LSTM方法与RNN等方法性能比较（%）

由表4可看出:在诊断精度上,基于LSTM模型明显优于典型浅层BPNN模型和SVM模型等2种传统诊断方法;与近年来应用的典型深层CNN模型和RNN模型相比,LSTM模型在准确率、精准率、召回率和F1-sore等4种分类性能指标上平均值更高,均达到99.91%以上。

基于同一数据集加入噪声后,笔者利用LSTM模型与其他4种方法的训练结果作进一步对比分析。与染噪前的数据类似,为了避免偶然性误差,每种方法各进行了10次试验,然后将各类评估指标的平均值作为该方法的分类诊断性能评估指标。

染噪声后,笔者利用LSTM方法与其他4种方法的4个评价指标,如表5所示。

表5 染噪声后LSTM方法与RNN等方法性能比较（%）

由表5可看出:当数据集中加入强噪声后,LSTM模型在准确率等4种分类性能指标的平均值仍然能达到99.32%以上,而CNN模型和RNN模型在准确率等4种分类性能指标的平均值均有所下降,分别下降了9.74%和9.08%;且BPNN模型和SVM模型在准确率等4种分类性能指标的平均值均出现大幅度下降,分别降低了12.42%和14.4%。

以上结果说明,LSTM模型能够稳定地对管路不同的健康状态进行识别。

该模型准确率高的原因在于,通过LSTM模型综合短序列高维特征进行了时序信息融合以及全面刻画了具备局部相关性的时序数据;经过LSTM模型的遗忘门处理后提高了信号的信噪比,避免了过拟合。