例谈直线的标准式参数方程在解题中的应用

崔 禹 李晓玲

(山东省桓台第一中学)

一般地,直线l的标准式参数方程为(t为参数),其中α为直线l的倾斜角,且α∈[0,π),直线l必过定点M0(x0,y0).

在直线l的标准式参数方程中,|t|表示直线上的动点M到定点M0的距离.

若直线l与曲线C相交于M1,M2两点,设点M1,M2对应的参数分别为t1,t2,则有如下结论成立:1)弦长|M1M2|＝|t1－t2|;2)若定点M0(x0,y0)为弦M1M2的中点,则t1＋t2＝0;3)若弦M1M2的中点为M,则点M对应的参数tM＝

1 求线段中点的坐标与线段长之和

点评一般地,遇到直线与曲线交于两点,往往需要先得到关于“t”的一元二次方程,再考虑利用根与系数的关系以及参数t的几何意义解题.

2 直线与圆相交,求线段长之和的取值范围

例2已知l是过定点P(4,2)且倾斜角为α的直线,圆C:x2＋y2－4x＝0.若直线l与圆C相交于不同的两点M,N,求|PM|＋|PN|的取值范围.

解析依据题意,可得直线l的参数方程为(t为参数),代入圆C的方程整理可得关于t的一元二次方程,即

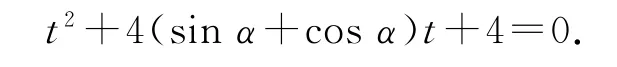
根据题设可知Δ＝16(sinα＋cosα)2－16＞0,化简得sinαcosα＞0.

从而t1＋t2＝－4(sinα＋cosα)＜0,又因为t1t2＝4＞0,所以t1＜0,t2＜0.

注意到点P(4,2)在直线l上,因此根据参数t的几何意义得

点评本题侧重考查直线与圆知识的综合运用,具有一定的难度,解题过程需关注两点:一是准确分析两个参数t1,t2与零的大小关系;二是根据Δ＞0分析倾斜角α的取值范围.

3 直线与抛物线相交,求弦长

例 3已知直线l的参数方程为(t为参数),求直线l被抛物线C:y2＝4x截得的线段AB的长.

点评本题极易出错,特别提醒——只有当t前的系数满足“平方和为1”时,直线的参数方程才是标准式参数方程.

4 直线与抛物线相交,求参数的值

于是,将式①和式②代入化简可得实数a＝1.

点评本题具有一定的综合性,求解过程需要关注两点:一是将|MN|是|PM|与|PN|的等比中项转化为|t1－t2|2＝|t1|·|t2|;二是灵活运用根与系数的关系及方程思想.

5 求焦半径倒数之和的值

点评运用“直线参数t的几何意义”这一解题方法时,往往需要考虑根与系数的关系才能较为顺利地进行化简、运算.运用根与系数的关系解题时,应熟练以下代数变形:

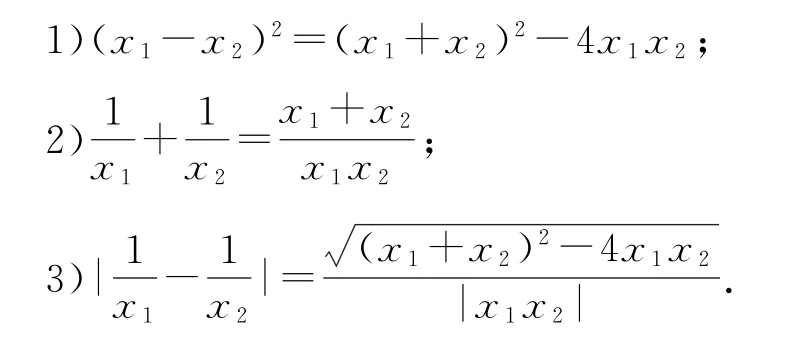
总而言之,遇到涉及与线段长度有关的求值或求解取值范围问题时,如果能够灵活运用直线的标准式参数方程,那么往往能化难为易,获得一个简捷、明了的解答过程.而解题的关键是必须明确直线的标准式参数方程中参数的几何意义;否则,较难顺利找到具体的解题思路,解题过程极易出错.

(完)