关于一个重要不等式链的几点注释
2022-10-26刘云
刘 云
(江苏省泰兴中学)
不等式是高中数学的重要基础知识,其中有一个需熟练掌握的重要不等式链
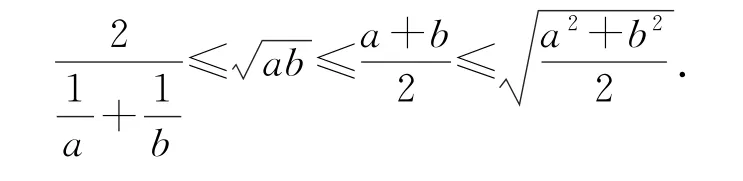
现给出其代数证明、几何解释以及相关练习,旨在从“数”与“形”以及应用角度,帮助读者进一步加深、拓宽对重要不等式链的准确理解与到位认识.
注:a>0,b>0 是重要不等式链成立的前提条件,其中是a,b的调和平均数,是a,b的几何平均数是a,b的算术平均数是a,b的平方平均数,而且a=b是其中每一个不等式取等号的充要条件.
1 重要不等式链的代数证明


2 重要不等式链的几何解释
如图1所示,点D,F均在圆O上,点C在圆O的直径AB上,AC=a,CB=b,并且DC⊥AB,FO⊥AB,连接DA,DO,DB,FC,经过点C作OD的垂线,垂足为E.根据图1 可知,圆O的半径r=

图1
(1)因为Rt△ADB斜边上的高为DC,所以由射影定理得DC2=AC·CB=ab,即DC=.又易知DO≥DC,所以可得不等式,当且仅当C,O两点重合,即a=b时不等式取等号.


3 重要不等式链的相关练习
例1若a>0,b>0,则称为a,b的调和平均数.如 图2 所 示,O为 线段AB的中点,以AB为直径作半圆,点C在线段AB上,且AC=a,CB=b.点D在圆弧上,作DC⊥AB,垂足为C.连接OD,AD,BD,过点C作OD的垂线,垂足为E.那么可知:图中线段OD的长度是a,b的算术平均数,线段_________的长度是a,b的几何平均数,线段________的长度是a,b的调和平均数.

图2
解析因为DC是Rt△ADB斜边上的高,所以根据射影定理得CD2=AC·CB,所以CD=,即线段CD的长度为a,b的几何平均数.

于是,可 知OE=从而DE=OD-OE=,即DE的长度为a,b的调和平均数.
例2甲、乙两位采购员同去一家粮食销售公司买了两次粮食,两次粮食的价格不同,两位采购员的购粮方式也不同.其中,甲每次购买1000kg,乙每次购粮用去1000元钱,谁的购粮方式更合算?

点评通过本题的层层求解,可知以真实生活问题为素材,通过细致分析可获得一个重要不等式——如果a>0,b>0,a≠b,那么不等式成立.
(完)
