强基计划数学备考系列讲座(9)——方程和不等式

王慧兴(正高级教师 特级教师)

(清华大学附属中学)

1 知识与技能

相关基本概念和知识技能如表1所示.

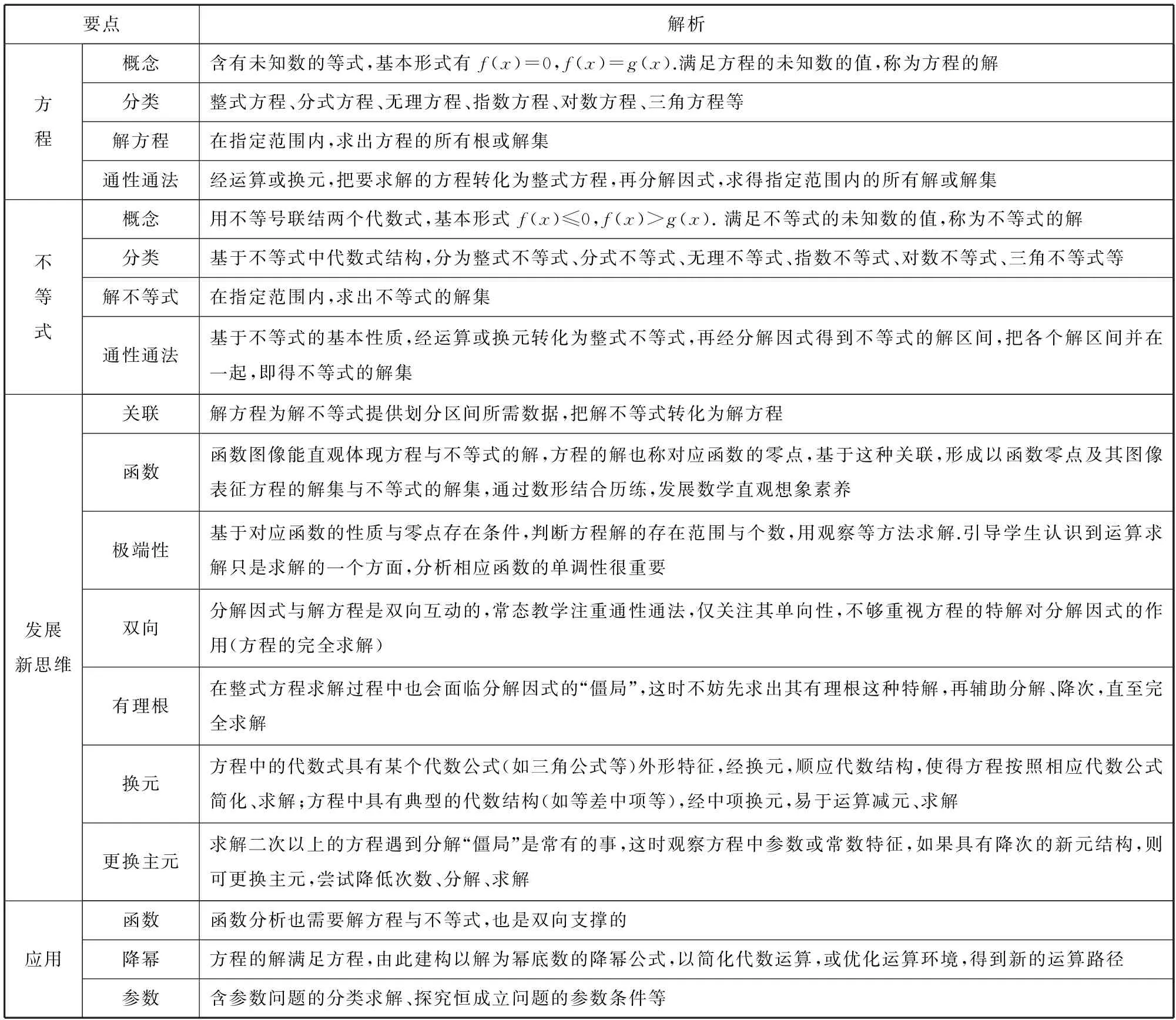
表1

2 典例精析

2.1 既要严守程式,又要灵活变通

解方程与解不等式的通性通法是在初中学习伊始阶段形成的,在学生数学能力形成过程中起到重要作用.“灵活性”是数学学习不可回避的特征,高校强基校测命题每年都会出现检测代数式灵活变形能力的题目.这意味着求解问题只满足于通性通法是不够的,针对新情境,需要不断发展新思维,使得通法不断得以完善与丰富,不能僵化理解、运用通法分析代数结构,追求情境转化是数学永恒的呼唤.

例1解不等式－

解析按通法求解,要按2－x的正、负分类求解,无视代数结构优势,直接分类求解,既会导致求解过程烦琐,也较为盲目,容易出错.其实,遇到一次分式代数结构,无论是解方程、解不等式、还是画函数图像或求值域,其基本路径是把分子化为常数.故

故不等式的解集为(－2,1).

例2解不等式

解析本例如果僵化地使用通性通法,要先将不等式转化为整式不等式,是很费劲的.基于函数观点,由于函数f(x)＝(0,13))严格单调递减,因此f(x)在其定义域(0,13)上有唯一零点x0.先考虑极端情形x∈{1,2,3,…,11,12},从两边逐步计算

例3(复旦大学)在实数范围内解方程

例4(上海交通大学)设k≥9,解关于x的方程x3＋2kx2＋k2x＋9k＋27＝0.

解析三次方程不是高中数学常态学习的基本内容,学生不知其特定解法,其基本求解路径是经分解因式、降幂,将方程转化为二次方程与一次方程求解.但其原本形式最高次项系数是1、常数项是一次的,代数上不能分解;再由于仅一项含k2,因此也看不出特解.考虑更换主元,以参数k作主元,调结构如下.

A.(x,y,z)只有1组

B.(x,y,z)有4组

C.x,y,z均为有理数

D.x,y,z均为无理数.

解析解方程组的基本路径是消元,先化为某个元的单变量方程,求出它的值,再计算其他变元的值.基于方程组代数结构,分别对两个变元x,z与y,w的基本对称多项式换元,令

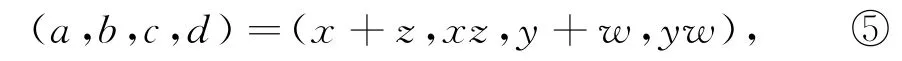
则原方程组可转化为

点评作为2006年全国高中数学联赛的压轴题,其本质是一道利用数列递推计算的题目,与国内外历届的试题相比,设计独到、新颖,与前面消元法相比,算法呈现出规律性,淡化了技巧.

2.2 函数思想与数形结合

在解复杂方程情境中隐藏着多种多样的代数结构,顺应结构优势,发掘各种算法引领求解前行,或构建函数降次,情境得以简化.

例7解关于x的不等式

log2(x12＋3x10＋5x8＋3x6＋1)＜1＋log2(x4＋1).

解析按照通法,去掉不等式两边的对数符号,整理可得

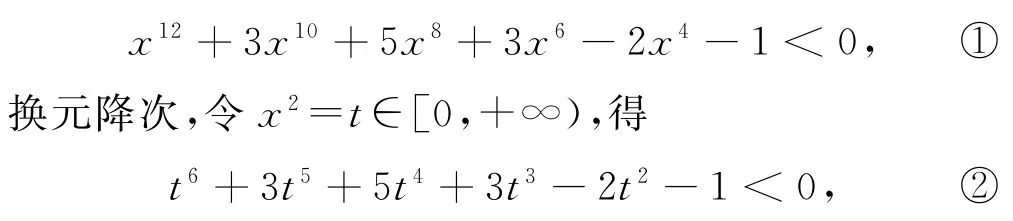
因为±1 都不是函数f(t)＝t6＋3t5＋5t4＋3t3－2t2－1的零点,这表明命题者在以这个不等式为载体考查某个特定的无理数,但无理数没有有效的判别法,因此可以考虑零点存在定理,通过计算、引领、跟踪该无理根(如表2).

表2

由此判定,函数f(t)在区间(0.5,0.625)内存在无理零点,联想到黄金分割比,猜想进一步猜想f(t)含有因式

另解当t＞0时,对不等式②调结构,得

恢复为变量x,即求得解集(以下求解过程略).

2.3 不等式与最值

理论上利用导数分析函数的单调区间是探究最值的基本路径,但在具体情境中,会面临着复杂的计算,容易陷入烦琐计算或根本没有办法完成笔算.因此,应对复杂情境最值计算还应多法并举.

表3

综上,fmin(x)＝,并且存在唯一极大值

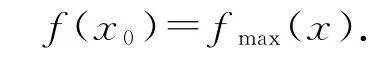
求法一:求导函数的唯一零点,再计算(读者可自行求解,解方程比较烦琐).

求法二:不用导数,应用均值不等式.

把参数值代入①②③累加,得

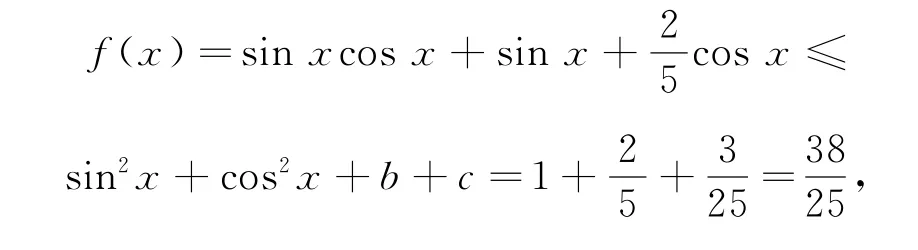
其中等号成立的条件是tanx＝,所以

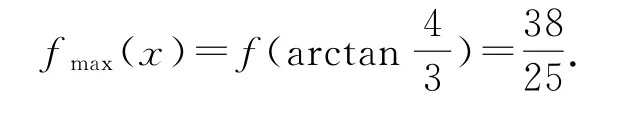
2.4 以方程降幂,构建递推算法

基于方程构造降幂公式是降幂、求值的一条递推路径.

例9计算的值.

解析若按照幂的概念直接计算,由于次数高,则难以正确计算.因此构造以幂底数为根的方程,能够建立降幂算法、递推计算.

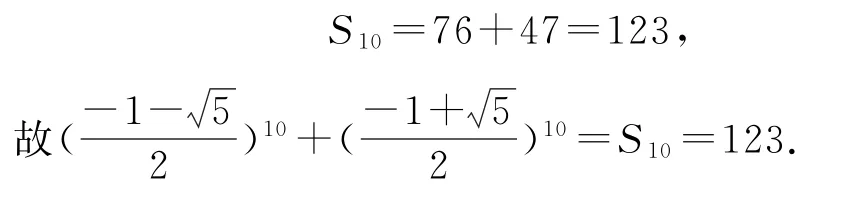
例10求最大的实数m,使得对一切满足a＋b＋c＝1的正数a,b,c,都有

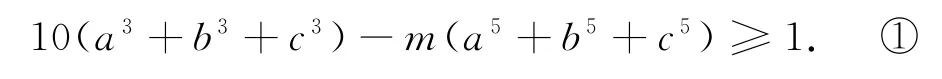
解析一方面,取a＝b＝c＝,代入不等式①,得

另一方面,下证mmax≥9,即证m＝9满足题设,亦即证明对一切满足a＋b＋c＝1 的正数a,b,c,都有

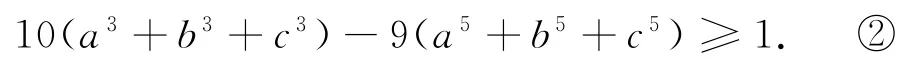
不等式②其实可以分离变量,令f(x)＝10x3－9x5,得

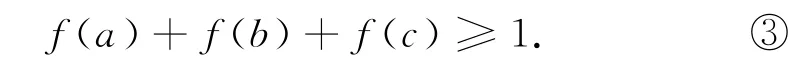
按照熟悉的证明路径,可以求出函数f(x)＝10x3－9x5在点的切线方程

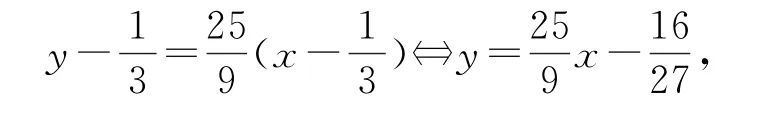
失败是成功之母,以下考虑对不等式②降幂处理.

构造以a,b,c为根的方程,记

对于b,c可同样降幂,所以再对不等式②中三次等幂和与五次等幂和降幂,得＝1－2u,且

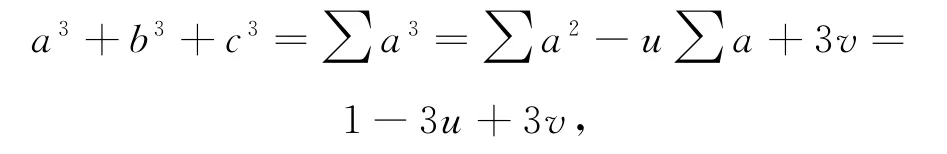
2.5 函数方程与不等式

2.6 组合分析

具有组合结构的代数问题,其求解路径通常为组合构造方法,如构造一批数据,用抽屉原理证明满足要求的数据结构存在.组合情境不同,其思维路径也不同.

情形二,数组中不存在等值数,则其中共有2n个数,剔除其中那个0值数,还有2n－1个正数.

把区间(0,1]划分为2n－1段,则

3 实战演练

11.(清华大学)在平面直角坐标系xOy中,已知A(－1,0),B(1,0),若对y轴上任意n个不同点Pi(i＝1,2,…,n),总存在两点Pi,Pj(1≤i＜j≤n),使得|sin∠APiB－sin ∠APjB|≤,则正整数n的最小值为( ).

A.3 B.4 C.5 D.6

12.(清华大学)设实数xi∈[0,1](i＝1,2,…,21),则f(x1,x2,…,x21)＝的最大值是( ).

A.110 B . 1 20

C.220 D.240

13.(上海交通大学)若函数f(x)＝ax2＋bx＋c(a≠0),且f(x)＝x没有实数根,则f(f(x))＝x是否有实数根? 请证明你的结论.

(完)