强基计划中的复数问题
——以清华、北大的校测笔试试题为例
2022-10-26唐浩哲
唐浩哲
(北京市十一学校)
强基计划目标是选拔有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生,选拔依据主要是考生高考成绩和高校的校测成绩.在大学里,复数是复变函数课程的基础,也是电磁学、量子力学等理工科课程的重要工具,因此复数成为了各高校强基校测笔试的热门考点.从近3年清华和北大两所高校校测笔试试题来看,复数问题主要涉及复数的代数形式、三角形式、单位根等内容,又与函数、方程、不等式、向量等相结合.

点评本题考查了复数的三角形式和乘除运算,比较灵活.也可以用特殊值法求解:令z1=1,解得z2=1±2i,则
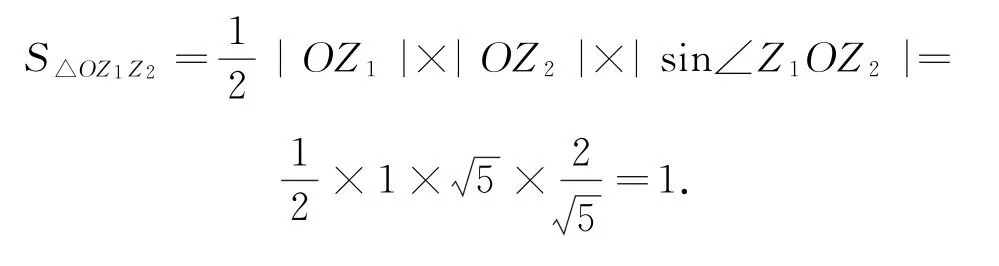
例2(2020 年清华大学)复数z满足|3z-7i|=3,令z1=,则|z1|的( ).

点评求解本题的关键在于先对z1进行化简,避开烦琐的计算,再利用复数的几何意义求解.
例3(2020 年清华大学)已知f(z)=z10+,则( ).
A.f(z)=0存在实数解
B.f(z)=0共有20个不同的复数解
C.f(z)=0的复数解的模长都等于1
D.f(z)=0存在模长大于1的复数解


综上,f(z)=0 共有20 个虚根,且模长均为1,选BC.
点评本题用到了实系数方程的虚根是成对共轭出现的这一性质,再配合根与系数的关系求出方程①的共轭虚根的模长.

点评本题虽然涉及复数,但实际考查代数变形和根与系数的关系.通过变形和换元,巧妙地将待求式子转化为一个新方程的所有根之和,再使用根与系数的关系求解.若把原式直接通分再用根与系数的关系代入计算,也可求出答案,但计算量比较大.
例5(2021年清华大学)设a,b是非零复数,z1,z2是方程x2+ax+b=0 的两个复根,且|z1+z2|=|z1|+|z2|,则( ).
A.存在正实数λ,使得z2=λz1
B.b是正实数
C.存在实数μ≥4,使得a2=μb
D.存在正实数ν,使得a=νz1
解析由|z1+z2|=|z1|+|z2|,可知z1,z2在复平面上对应的向量同方向,则z2=λz1(λ>0),A 正确;a=-(z1+z2)=-(1+λ)z1,D 错误;b=z1z2=,B 错 误;μ=+2≥4,C正确.
综上,选AC.
点评求解本题的关键在于结合复数的几何意义理解条件|z1+z2|=|z1|+|z2|.
例6(2021年清华大学)设n是正整数,模长为1的复数z满足zn+z+1=0,则( ).
A.|z+1|=1 B.z的实数部分为-
C.n-2是3的倍数 D.满足条件的z是唯一的
解析依题意,zn,z,1在复平面内对应的3个模长为1的向量可以首尾相连成封闭的三角形,结合几何作图可知

故A,B正确,D 错误;无论是哪种情况,都有zn=z2,因此n-2是3的倍数,C正确.
综上,选ABC.


点评本题考查了复数的单位根,对于这一类问题,一定要寻求整体变形和代换,并利用好对称性,而不能陷入零碎的计算之中.
例8(2021年北京大学)设f(x)=x2+2x+2,定义f(1)(x)=f(x),对n≥1,定义f(n+1)(x)=f(f(n)(x)),则方程f(2021)(x)=0 所有复根的平均值为( ).
A.-1 B.-2
C.-2022 D.前三个答案都不对
解析设f(2020)(x)=0 的所有复根为t1,t2,…,tm,由f(2021)(x)=f(f(2020)(x)),可 知f(2021)(x)=0 的所有复根由m个方程f(x)=tk(k=1,2,…,m)的复根所构成.注意到对任意的k=1,2,…,m,f(x)=tk都有两个复根,且这两个复根的平均值均为-1,所以方程f(2021)(x)=0所有复根的平均值为-1,故选A.
点评本题也可以先从求f(x)=0和f(f(x))=0的复根的平均值这一简单的情况入手,形成初步的猜想和解题思路,再探讨一般情况.
例9(2022年清华大学)在复平面上,复数z1在连接点1+i和1+ai(a∈R)的线段上,复数z2在以原点为圆心,半径为1的圆上.若点z1+z2的可能位置所组成的图形面积为4+π,则a的值为( ).
A.-1 B.1
C.3 D.5
解析当a>1时,z1+z2在复平面所对应的区域是以(1,1)为圆心,1为半径的圆周向上平移a-1个单位时扫过的区域.该区域可看成是上半圆、下半圆以及中间的一个矩形,即+2(a-1)+=4+π,解得a=3.当a<1时,同理可得a=-1.
综上,选AC.
点评求解本题的难点在于对z1+z2的几何意义的认识.
例10(2022年清华大学)复数z满足|z|=1,则|(z-2)(z+1)2|的最大值为( ).
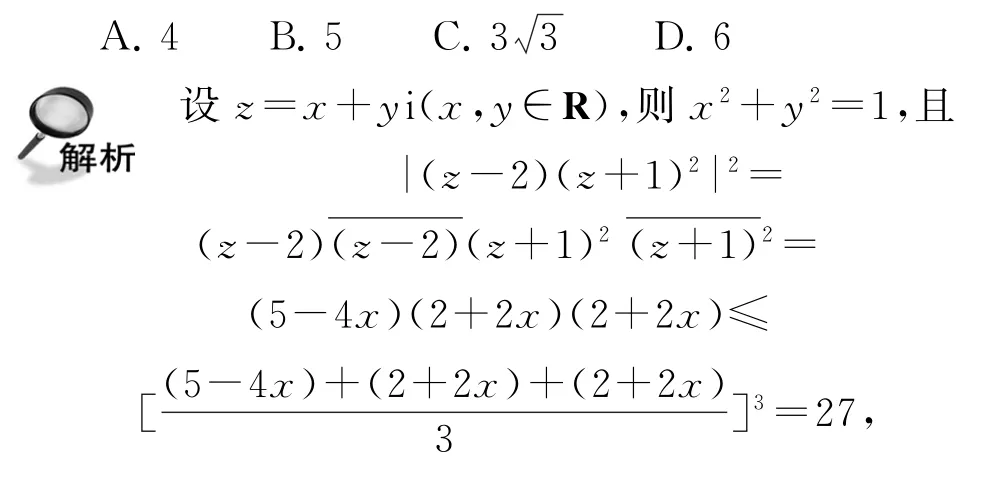
所以|(z-2)(z+1)2|的最大值为,选C.
点评本题的变形依据是,后续用到了三元均值不等式,也可以通过求导来确定三次函数的最值.
例11(2022年北京大学)已知复数z满足和的实部和虚部均属于[-1,1],则z在复平面上形成的轨迹的面积为( ).
A.8 B.12-2π
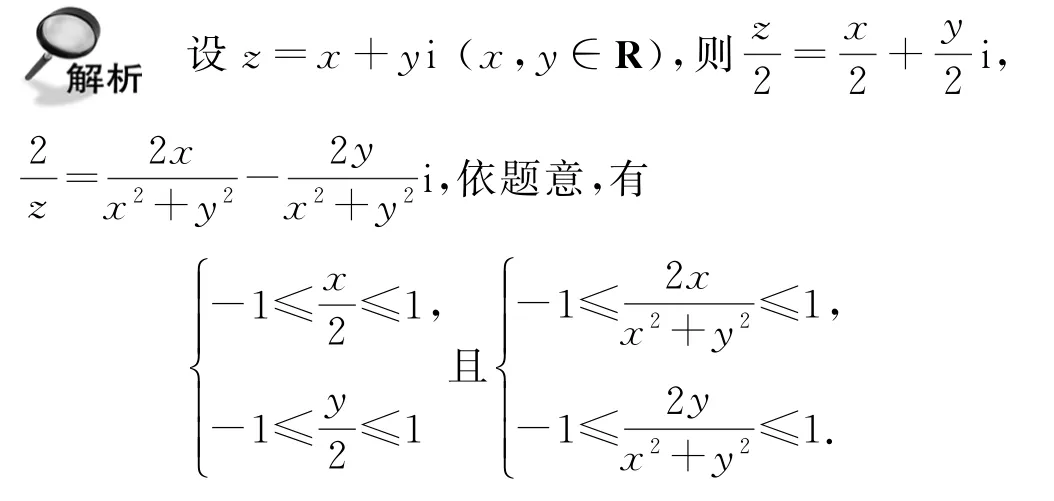
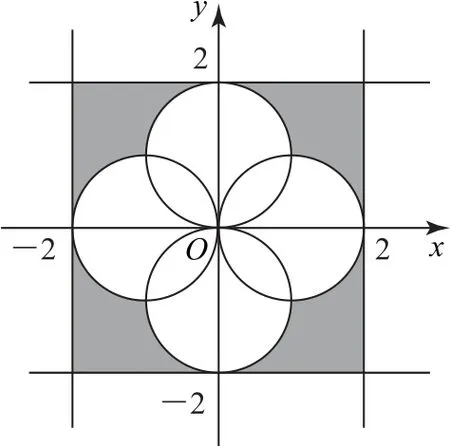
图1
点评本题和例10都考查了复数的代数形式,此类题型难度不大,但需要在明晰相关概念的前提下准确计算.
(完)
