核心素养背景下初中数学项目式学习

上海市卢湾中学 李 佼

《义务教育数学课程标准（2022年版）》指出，初中阶段的核心素养主要表现为：抽象能力、运算能力、几何直观、空间观念、推理能力、数据观念、模型观念、应用意识、创新意识。夏雪梅教授在《项目化学习设计：学习素养视角下的国际与本土实践》中提出六维度项目化学习框架：①核心知识；②驱动性问题；③高阶认识；④学习实践；⑤公开成果；⑥全程评价。此框架为开展项目学习提供了设计模板，通过项目学习，建立起学科知识与真实世界之间的联系，培养学生核心素养。

沪教版七年级下册第十五章“平面直角坐标系”是数形结合的平台，是学生学习函数图像和平面解析几何的必要基础。平面直角坐标系的建立，是数轴概念的发展和理性思维的成果，同时又有现实生活经验的基础。对平面直角坐标系的学习，学生不仅需要理解其相关知识，还需要体会平面直角坐标系与实际生活的联系，能从实际情境中抽象出数学概念，建立模型，用数形结合的思想方法来解决相应问题。基于此，笔者积极探索如何通过项目学习，帮助学生理解数学与生活的联系，培养其抽象能力、模型观念、应用意识、创新意识等核心素养。

一、项目开发背景

五子棋游戏起源于中国古代的传统黑白棋种之一，它简单易学、趣味无穷，是一种两人对弈的纯策略型棋类游戏。沪教版七年级下册第十五章“平面直角坐标系”的探究活动二提出的就是五子棋的相关内容。教材中，通过一种新的棋谱记法，学生可以将生活中的实际问题数学化，用数学语言来描述棋子的位置。在此基础上，笔者发现五子棋棋谱是网格式的，与平面直角坐标系类似，棋手在训练过程中，记录棋子的方式是通过横向的阿拉伯数字和纵向的英文字母组合而成，这与平面直角坐标系中点的表示方法类似，由此可抽象出与平面直角坐标系的关系，建立数学模型。因此，笔者决定以五子棋游戏为背景，联系平面直角坐标系的知识，结合其他对弈游戏的规则，让学生从玩者变成设计者，加入数学元素重新设计五子棋游戏规则，“巧玩五子棋”这个项目也就应运而生。

二、项目设计

在项目设计之初，我们先整理了平面直角坐标系的相关知识点（如图1），确立了知识发展序列。基于知识发展序列，设计与之相匹配的项目任务线。在北京师范大学专家团队的指导下，经过几次修改完善，我们确定了项目的驱动性问题和本质问题，对整个项目的内容进行了设计。

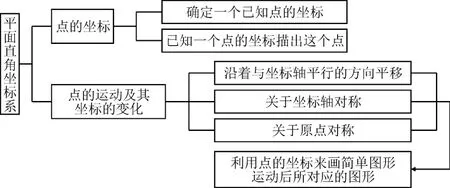
图1 “平面直角坐标系”知识结构图

（一）项目任务

项目的具体实施需要明确的任务规划。在本项目的本质问题（五子棋游戏的新规则设计）的驱动下，我们设计了三个任务来推进整个项目的进行。任务1是“设计新的棋谱记法”，这是新规则设计的基础，承载的知识点是“有序实数对”及“平面直角坐标系的概念”；任务2是“五子棋新规则的基础版”，这是在常规规则的基础上增加一点难度，比如，说出棋子的坐标等，承载的知识点是“用坐标表示平面内的点”“垂直于坐标轴上的直线的表示方法及平行于坐标轴的直线上的两点的距离”；任务3是“五子棋新规则的进阶版”，任务2中棋盘上的棋子是不动的，但在任务3中，棋盘上的棋子可以像象棋一样进行移动，这也是形成完整的设计方案的最终任务，承载的知识点是“直角坐标系中的平移、轴对称、中心对称”。

（二）问题序列与知识发展

按照“以任务推进为明线，以知识发展为暗线”的原则，在三个项目任务的驱动下，我们对每个任务设置了问题序列，合理地将相关数学知识承载于各个问题中（如表1）。整个设计通过问题链的形式将项目的任务线与数学知识同时推进，两者之间相互融合，不仅形成项目的最终成果，也落实相关的数学知识，培养了学生的学科素养。

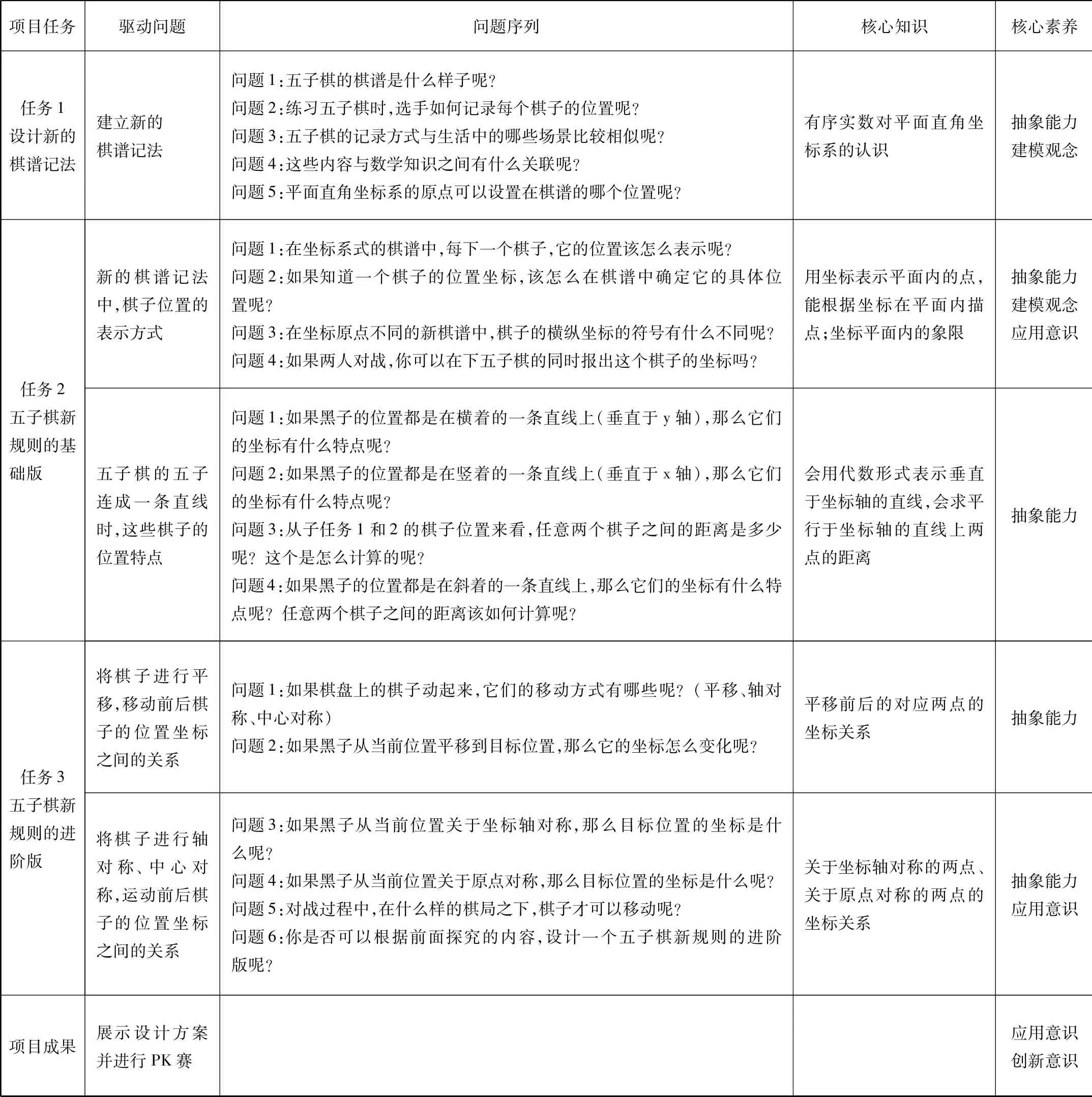
表1 “巧玩五子棋”项目设计框架

三、项目实施

针对整个项目的实施，笔者主要介绍最后展示课的实施过程。最后的展示课分为四个环节：整理回顾、成果展示、小组PK赛、总结评价。

第一，整理回顾。在之前的学习中，学生对整个项目的背景、任务及所学的数学知识十分了解，但学生关注更多的是局部知识的学习和应用，通过回顾整理，学生对项目的整体有了新的认识，能从整体的角度去理解整个项目的学习。

第二，成果展示。这个环节主要是每个小组展示分享五子棋新规则的设计方案，其他小组根据他们分享的情况进行提问，给出评价，在所有小组展示结束后，评选出最佳方案。评价的要素包括学科知识的使用，规则设计的合理性、创新性等，以及语言表达能力情况。通过提问、回答，学生可以跳出自己的思维，重新审视设计的规则，有助于之后的修改、完善。经过展示，学生语言表达能力有所提高，也体会了团队合作的重要性。

第三，小组PK赛。此环节的具体设置如下：PK赛的裁判和相关工作人员是最佳方案小组成员，具体的五子棋规则按照他们的设计方案来进行，其他小组进行抽签决定PK对象，完成整个PK赛。这个环节的巧妙之处在于五子棋规则的选择，获得最佳方案的设计也可以通过实践来验证它们的合理性、可行性，不仅使比赛公平公正，也让他们意识到理论与实践相结合的重要性。

第四，评价总结。具体分为学生总结和教师总结。学生可以对自己在整个项目的所学所得进行总结，也可以对自己的整个学习过程做自我评价。教师对整个项目的开展实施和学生在整个项目中遇到的问题以及如何解决问题等进行总结。

课后作业是针对在展示交流中，大家对设计方案提出的问题进行进一步的修改完善，形成最终的成果。

四、项目反思

基于教材单元内容，此项目从探究活动出发，以真实情境为切入点设计驱动性问题，通过解决问题，形成与实际生活相关的项目成果。整个过程中以项目任务为明线，数学知识为暗线，双线逐步推进，相互融合，学生在“玩”中学，学中“玩”，体会到数学知识在实际生活中的运用，感受到数学来源于生活又服务于生活。

（一）对项目设计的反思

在具体实施过程中，整个设计和课堂呈现还有一定的不足之处。北京师范大学的专家团队也对整个教学设计进行了多次指导，其中吉林师范大学的郝连明副教授提出展示课中的整理回顾可以放在最后的总结评价中进行，展示之后再整体总结，效果会更好；展示过程中，对作品的要求可以指向更为具体的数学知识；评价内容可以进一步关注非认知因素。

（二）自身成长

通过这次项目开发和实施，笔者明确了项目背景需要简单扼要，通过引入话题，指明方向，引起学生的兴趣，告诉学生“这个项目将要干什么”；在确定项目目标时，需要将项目任务与数学知识联系起来，突出做中学，一般项目目标只需要三四个即可；在进行具体的教学设计时，需要将任务线和数学知识相互融合，在推进项目任务的同时掌握相应的数学知识。

（三）后续学习

项目式学习是学生学习的过程，也是加强学生综合与实践能力的一种重要的学习方式。项目式学习以用数学方法解决现实问题为主，引导学生发现、解决现实问题，用数学的思维分析要素之间的关系，培养模型观念，培养应用意识和创新意识。对之后的项目开发，除了参考教材上的探究活动外，也可以多留心生活中的实际问题、社会热点问题，多思考这些问题与数学知识的联系，挖掘适合现阶段学生的知识点，让学生可以在真实情境中用适切的数学语言表达相关问题，解决问题，形成实际有效的项目成果。

（四）项目延续性

虽然这个项目是在七年级进行的，但这个项目还具有延续性。在七年级，要求掌握平行于坐标轴的两点的距离公式，而棋盘上任意两点之间的距离涉及的知识是八年级的勾股定理和两点间的距离公式；在七年级，要求掌握垂直于坐标轴的直线的代数表示形式，但若五子斜着连成一条直线，这条直线的代数表示形式涉及的是八年级的一次函数的内容，所以这个项目在八年级也可以进行。同时，学生玩五子棋游戏的水平高低，派哪位成员代表小组出赛等，这些内容涉及的是九年级的统计初步，所以在学习这些数学知识时，也可以考虑五子棋项目。这个项目在后续还有很多可开发的点，需要我们继续努力，认真研究。