Monocular Visual-Inertial and Robotic-Arm Calibration in a Unifying Framework

Yinlong Zhang,, Wei Liang, Senior, Mingze Yuan, Hongsheng He,, Jindong Tan,, and Zhibo Pang, Senior

Abstract—Reliable and accurate calibration for camera, inertial measurement unit (IMU) and robot is a critical prerequisite for visual-inertial based robot pose estimation and surrounding environment perception. However, traditional calibrations suffer inaccuracy and inconsistency. To address these problems, this paper proposes a monocular visual-inertial and robotic-arm calibration in a unifying framework. In our method, the spatial relationship is geometrically correlated between the sensing units and robotic arm. The decoupled estimations on rotation and translation could reduce the coupled errors during the optimization. Additionally, the robotic calibration moving trajectory has been designed in a spiral pattern that enables full excitations on 6 DOF motions repeatably and consistently. The calibration has been evaluated on our developed platform. In the experiments, the calibration achieves the accuracy with rotation and translation RMSEs less than 0.7° and 0.01 m, respectively.The comparisons with state-of-the-art results prove our calibration consistency, accuracy and effectiveness.

I. INTRODUCTION

MONOCULAR visual-inertial and robotic-arm calibration aims at correlating the spatial relationship between the visual-inertial unit and robot. Typically, monocular camera and inertial measurement unit (IMU) form a compact and minimum sensor suite. They could be potentially used for robot pose estimation and surrounding environment perception [1]–[5].

Camera and IMU share heterogeneous features regarding their quick response, tracking accuracy, and absolute pose observability [6]–[9]. Camera belongs to the exteroceptive sensor type. It captures body pose by tracking the visual features (usually, the blob patterns, corners or pixel intensities) and minimizing reprojection errors or photometric errors over image sequence. Comparably, IMU belongs to the proprioceptive type that captures body inertial measurements,i.e., linear accelerations and angular velocities. The absolute metric scale, gravity and short-term yaw-pitch-roll angles could be derived [10], [11]. Through this way, robot tracking works even in presence of camera tracking failures such as illumination changes, motion blurs, and absence of textures[12], [13]. Potential areas for visual-inertial based robot perception include visual-inertial odometry for unmanned aerial vehicle and ground vehicle, robotic arm motion tracking, etc [14]–[17].

Basically, the performance of monocular visual-inertial based robot pose estimation and surrounding environment perception considerably relies on the accuracy of calibration among the triplet [18]–[22]. Incorrect calibration will result in severe drifts over time, which is unacceptable for high-end industrial robot perception. The existing literatures on visualinertial calibration can be classified into two categories: offline and online [23]. Off-line calibration, as the name suggests, performs the spatial and temporal calibration before use [7], [24], [25]. The calibration process usually requires users to gently and evenly move the sensor rig in front of a stationary target (typically a chessboard or april tags). The whole process repeats a few times until convergence.Generally, the calibration result has relatively higher precision and consistency, since it enables batch optimization over a large visual-inertial dataset. While, for online calibration, the extrinsic parameters as well as the body initial values (e.g.,velocity, pitch, and roll) are estimated online [26]. The angular velocity and acceleration biases could be estimated to compensate for temperature changes. However, the calibration performance, sometimes, is not quite stable compared to offline ones, since the calibration process only lasts a few seconds and lacks repeatability.

The general goal is to design a visual-inertial & robotic-arm calibration method (illustrated in Fig. 1). In order to solve the inherent calibration issues (for instance, inconsistent calibration movement, unexpected disturbances while holding the visual-inertial rig, absence of adequate excitations on 6-DOF movement), this work designs an accurate and consistent moving trajectory, which is performed by the 6-DOF robotic arm. The trajectory could excite yaw-pitch-roll rotations andx-y-ztranslations evenly and repeatably. Besides, we develop a unifying model that is able to correlate the spatial relationships among the triplet in an elegant mathematical formulation. The contributions of this paper are summarized as follows.

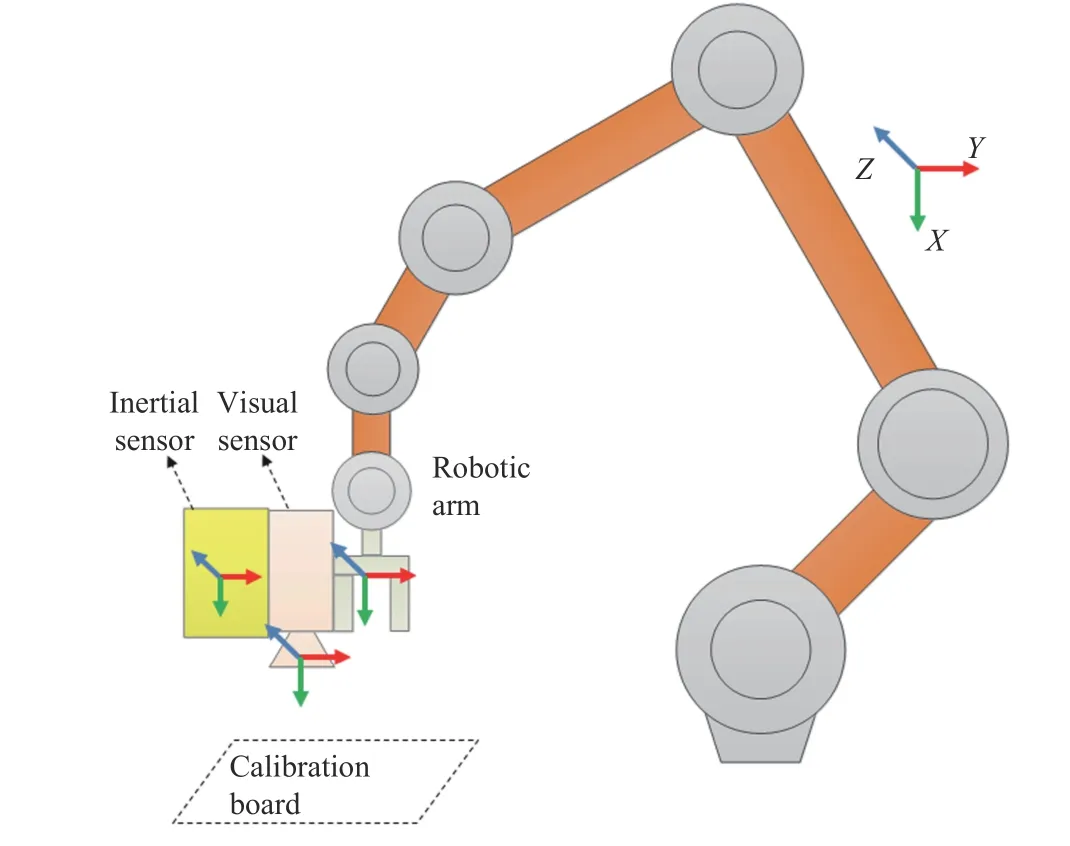
Fig. 1. Illustration on our proposed method: visual-inertial and robotic-arm calibration. The coordinate frames include camera frame, IMU frame and robotic-arm frame. The goal is to estimate the visual and inertial intrinsics, as well as the spatial relationships among visual-inertial and robotic-arm frames.

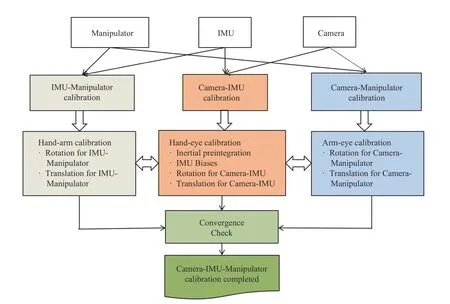
Fig. 2. Pipeline of our calibration on camera, IMU and Robotic arm system. It consists of three parts: IMU-Manipulator calibration, Camera-IMU calibration,and Camera-Manipulator calibration. Afterwards, the calibration parameters are fed into the convergence model for sanity check.

i) A monocular visual-inertial and robotic-arm calibration model is developed in a unifying framework;

ii) We design a spiral moving trajectory that could excite yaw-pitch-roll rotations andx-y-ztranslations evenly,uniformly and repeatably. The unexpected moving jitters and disturbances could be alleviated.

iii) The proposed method has been evaluated on our developed platform. The repeatability tests, systematic analysis and comparisons with state-of-the-art results have been extensively performed to prove our method effectiveness.

The rest of the paper is organized as follows. In Section II,the related works on visual-inertial-robot calibrations are reviewed. In Section III, preliminaries on variable notation and IMU model are briefly introduced. In Section IV, our proposed method is described in detail. In Section V, the developed platform is briefly introduced; the calibrations are extensively analyzed and compared with state-of-the-art results. Section VI concludes the whole paper.

II. RELATED WORK

A. Camera-IMU Calibration

By and large, camera-IMU calibrations can be classified into two types, i.e., online and offline. Online calibration aims at correlating the spatial relationship between visual-inertial sensors rightly before use. The calibration usually performs in a plug-and-play manner. In [27], Yanget al.analyzed the observability for spatial and temporal calibration parameters of visual-inertial sensors and it has been verified that calibrations are observable for random motions rather than degraded motions (e.g., planar motion) which might result in the occurrence of calibration failures. Similarly, Kelly and Sukhatme showed that the relative observability of visualinertial transformation needs the platform to undergo both accelerations and rotations in more than two IMU axes in[19]. Moreover, [28] introduced a closed-form method to estimate visual-inertial orientation, speeds, scales and biases.In [29], Zhenget al.estimated the calibration parameters within the filtering framework for ground vehicle VIO. In[26], [30], Yanget al.proposed to calculate camera-IMU time offset, relative transformation and inertial biases in the VINS framework. Basically, online calibration fits the plug-and-play scenario such as unmanned aerial vehicles (MAV) odometry.

Offline calibration calibrates camera and IMU sensor suite in advance. It needs a larger number of calibration datasets and achieves more accurate and reliable calibrations. In [31],Lobo and Dias estimated the rotation and translation between camera and IMU in a separate manner. The rotation is firstly calculated by aligning visual sensor orientation with gravitational components (obtained by inertial accelerations).The translation is computed by using the encoder and turnable. However, it needs to precisely place IMU right at the center and camera at the rim of turntable, which requires expertise and patience to follow the procedures. In [32], the rotation is estimated in form of quaternions. Afterwards,slerping is applied to synchronize the visual-inertial measurements. The rotational matrix is computed by aligning the quaternion rotating axes, which leaves alone the angle part from the derived quaternion. Through this way, the noises in rotational angle components from quaternions could be suppressed. In [33], Furgaleet al.proposed to estimate both the temporal offset and spatial transformation in a joint framework. It minimizes the error terms that relate to tracking feature reprojections, inertial accelerations, velocities and biases. Generally, the offline calibration is more accurate than online ones in that the moving trajectories could be repeated and estimation inconsistency could be alleviated. Additionally, the camera and IMU measurements characterize in highdimensional and sparse space [34], which could be further used to extract nonnegative latent useful information via the NLF model in the offline mode, which are extensively analyzed by Luoet al.in [35], [36].

B. Camera and Robotic-Arm Calibration

In the camera and robotic-arm calibration, rotation and translation between camera frame and robotic-arm frame are computed by tracking calibration board features from different viewpoints. Afterwards, the reprojection minimization is implemented to align the adjoint attitudes [37]. The cameraand robotic arm calibration are also categorized into two types, i.e., eye-in-hand mode and eye-to-hand mode.

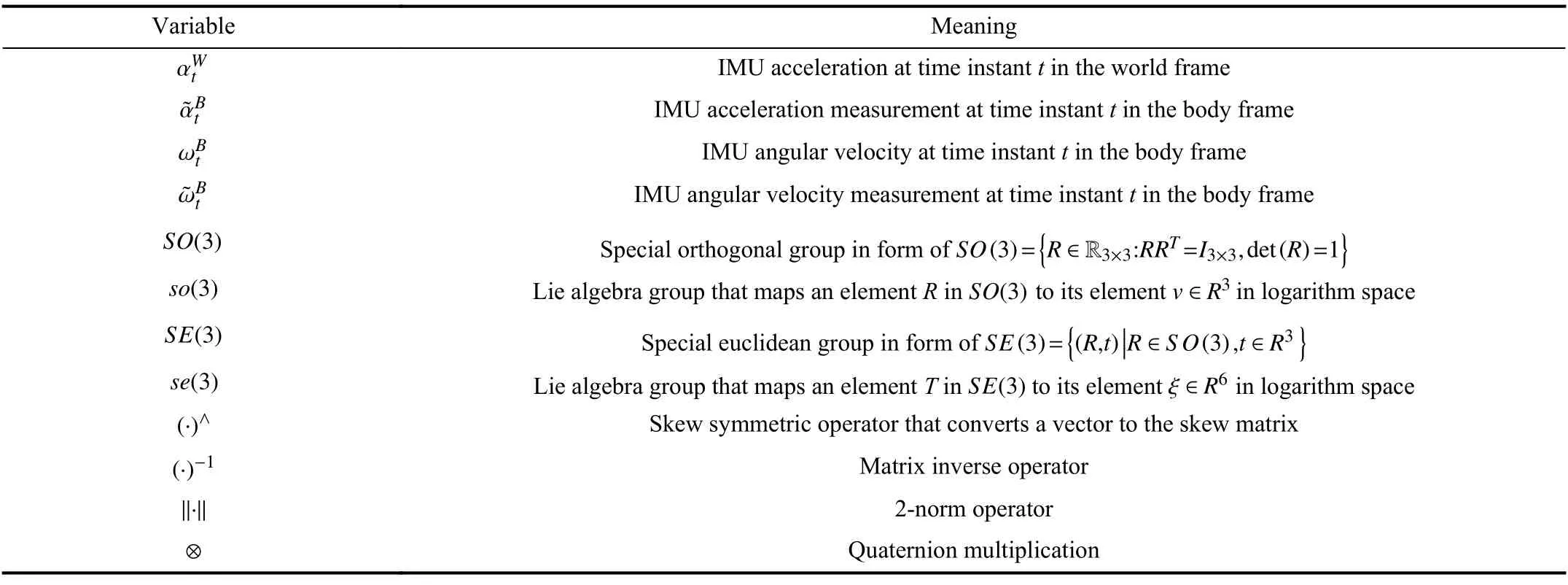
TABLE I NOMENCLATURE

In [38], [39], Liet al.introduced a comprehensive overview of calibration on industrial robots and dual arms. By taking measurement noise and external constraints into the robot kinematic model, the calibration accuracy could be boosted. In terms of eye-in-hand type, camera is rigidly mounted to robotic arm. The calibration board moves within the camera captured views. In [40], the authors proposed a unified mathematical formulation by using procrustes analyzers. In[41], the authors introduced an eye-in-hand calibration for the scanner robotic system. By cyclically capturing images from a 2d calibration object, the calibration kinematic model parameters are obtained. For the eye-to-hand calibration type,camera is fixed in a global-view fashion. Robot holds the checker board and moves within the camera capturing view.In [42], Koide and Menegatti introduced to directly take images with calibration patterns in the pose graph optimization model. In [43], the authors presented the calibration that minimizes two kinematic loop errors. By and large, the eye-in-hand type is preferable because of its flexibility and first person view.

III. PRELIMINARIES

A. Variable Notations

The variables used in the paper are listed in Table I. The coordinate frames used in this paper include world frame {W},camera frame {C}, IMU frame {I} (also known as body frame{B}) , robot frame {R}. The transformation from camera frame{C} to IMU frame {I} is described by a 4 × 4 transformation matrixin its homogeneous form, which is given by

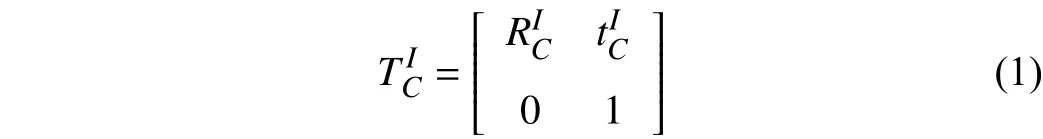
B. IMU Model

IMU consists of 3-axis accelerometers and 3-axis gyroscopes [44]. The accelerometer measures both local gravity accelerations and linear accelerations. Usually, they are corrupted by sensor noises, non-linear bias variations with temperature. Unfortunately, these errors will be accumulated and lead to significant drift in the position, attitude, and velocity outputs. Luckily, the inertial errors could be considerably compensated by complementary visual sensing unit.

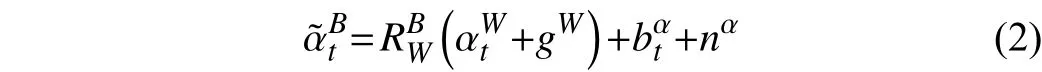
In this work, the acceleration model is given by [45]wheredenotes the linear acceleration in the world frame;denotes the sampled body accelerations in the body frame,which is coupled with gravitational parts and noises.gWis the gravitational vector in the world frame.is the rotation matrix from world frame to body frame.denotes the bias (which is caused by low-frequency offsets and changes over time slowly). Usually, it causes the majority of errors while double integrating the accelerations. In this work,is modeled as a random walk process [46].nαis the acceleration noise (usually taken as white Gaussian noise).

Similarly, the angular rate measurement model is

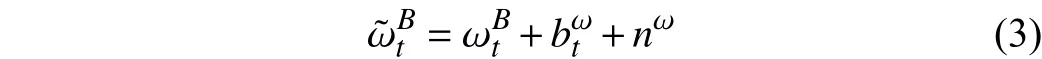
IV. METHOD

In this section, our method is described in detail. As illustrated in Fig. 2, it consists of three modules: camera-IMU calibration, camera-robot calibration, and IMU-robot calibration. For camera-IMU calibration, it includes the computations on IMU biases, coordinate rotations and translations.Then the IMU biases are fed into the calibration on IMU-robot module to derive the corresponding IMU-robot frame transformations. Meanwhile, camera and robot calibration is performed using the hand-eye calibration. The calibration completes when the triplet satisfies the convergence condition.The details are described in the following subsections.

A. Camera-IMU Calibration

In this work, camera-IMU calibration is divided into two parts, i.e., IMU preintegration and camera-IMU intrinsic &extrinsic calibration.

1) Inertial Measurement Preintegration:In order to align the transformation between camera and IMU, it is crucial to implement IMU preintegration [5]. Given time instantsiandjbetween camera successive frames, the body orientation,velocity and position could be preintegrated from the collected inertial measurements. They are given by

IMU measurements could be preintegrated that are only related to visual frames at timestiandtj. In (5a), the noise term could be isolated and approximated by its first-order Jacobian given as

Similarly, the increment in velocity could also be expressed by its first-order approximation given as

2) Camera-IMU Extrinsic and Intrinsic Calibration:In this work, we assume that the gyroscopic and acceleration biases remain constant. The biases can be calculated by minimizing the difference between IMU rotation and camera rotation iteratively. During the iteration, the estimated rotationis used to update the angular velocity bias.

a)Angular velocity bias estimation

The rotation of camera frame between timestandt+1 could be given by

By combining (4a), (6), and (11), the relationship between camera rotation and IMU preintegration of the time periodstandt+1 can be given by

Equation (13) could be solved using the Levenberg-Marquart nonlinear optimization. The preintegrations on IMU rotations are updated afterwards.

b)Camera-IMU rotation estimation

The rotation can be computed by aligning the camera rotation between framestandt+1 with the preintegrated IMU rotations. Assume the changes of attitude for camera frame and IMU frame areandrespectively between time interval [t,t+1].andrepresent the same rotation though in different coordinate reference systems. The quaternionthat converts the camera reference to IMU reference satisfies

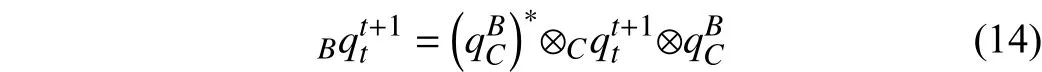
where ( ·)∗means quater nion conjugation.

Then the optimal quaternionwill be obtained by maximizing the following equation:

c)Accelerometer bias estimation

By combining (4b), (4c), and (11), the relationship between camera translation and inertial preintegrated translation during time interval [i,j] is

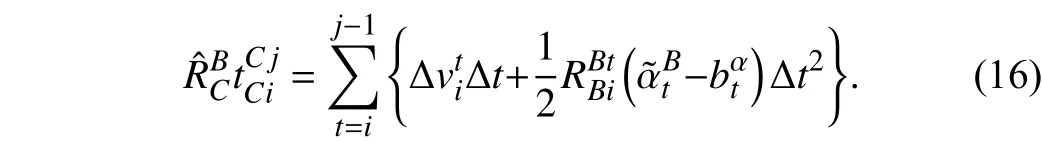
The optimal accelerometer biascould be obtained by minimizing the following function:

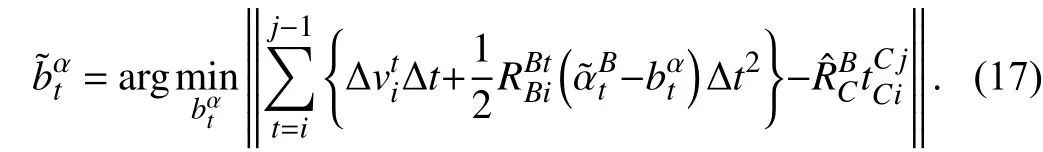
d)Camera-IMU translation estimation

B. Camera and Robotic-Arm Calibration

In this work, camera and IMU are rigidly attached to robotic wrist (the 6th joint of robotic arm). The camera and roboticarm calibration is expressed by the transformation matrix in its homogeneous form.

C. IMU and Robotic-Arm Calibration

IMU and robotic-arm calibration could be formulated by homogeneous transformationXRI[48]. The robotic wrist moves in a predefined trajectoryMeanwhile, IMU follows the similar path ({I1→I2→I3···},also seen as IMU pose sequence).

Similarly to (19), IMU and robotic wrist poses satisfy the following equation:

In a similar manner, the relative rotationRRIand translationtRIbetween IMU frame and robotic wrist frame could be derived by solving the following equations:

D. Calibration Convergence Criteria

In our model, there exists an inherent geometric constraint between robotic wrist frame {R} , IMU frame {I} and camera frame {C}. Theoretically, the transformation matricesTRC,TRI, andTICsatisfy the following geometric relationship:

E. Robotic Arm Calibration

Because of the structural parameter errors of robot and the robotic dynamics effects, the actual running trajectory of robot could, somehow, deviate from the programming values.However, the errors caused by the aforementioned issues could be compensated by calibrating the kinematic model of the robot dynamics factors (e.g., centrifugal force, coriolis force, dynamic coupling [38]). The robotic arm calibration model is briefly introduced in this section.

The robotic arm could be described by the multi-link mechanism connected by joints [49]. Its kinematics could be formulated by the D-H model, which is described as

wheresymbolizes the transformation matrix between the successive linksi−1 andi.cθ andsθ symbolize the trigonometric functions sinθ and cosθ, respectively. The group parameters {θi,αi,di,ai} are the variables associated with jointiand linki, which mean the joint angle, link length,link offset, and link twist, respectively. The link between the successive joints could be fully described by the D-H model.

Additionally, the moving trajectory could also be affected by the robot dynamics. Its dynamic model could be described in the form of Lagrangian equation as follows:

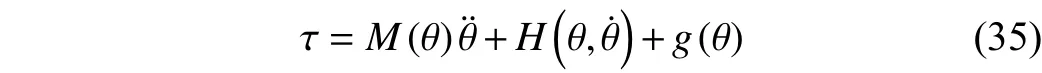
whereτsymbolizes the torque andθsymbolizes the joint angle;M(θ) means the inertial matrix;stands for Coriolis and centrifugal force;g(θ) is the gravity.

In this work, the least square method is used to calibrate the robot. It computes the inherent geometric parameters (i.e., link parameter error, joint rotation error) by minimizing the errors between the theoretical data and its measurement. In this paper, the 3-D schematic model of position measuring system with drawstring displacement configuration is adopted. Then the robot kinematic errors are calculated by minimizing the loss function of errors between the actual end-effector position and its measurement from the D-H model in (34). Please refer to [50] for more details in calibration implementation.

V. EXPERIMENTAL RESULTS AND ANALYSIS

A. Experimental Platform

In our developed system (shown in Fig. 3), the robotic arm is Kinova Jaco 2 with 6 rotation joints. The total weight of the robot is 5.2 kg. Its maximum reach is up to 98 cm and its maximum linear arm speed is 20 cm/s. Its communication protocol is RS-485 with USB 2.0 port. The commands are given on Linux Ubuntu & ROS system. Its maximum payload is 2.2 kg.

Fig. 3. The experimental platform consists of Camera, IMU, and Robotic arm. Intel D435i (integrated with monocular camera and IMU) is rigidly attached to the robotic-arm (Kinova Jaco 2) 6th joint. It is programmed to move in a predefined pattern to capture the calibration board and body inertial measurements.

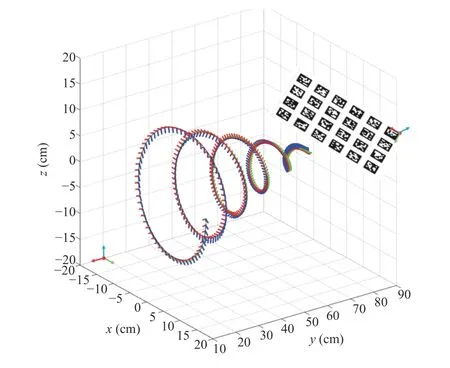
Fig. 4. Designed robotic arm moving trajectory. It moves in a spiral pattern.The x-y-z translations and yaw-pitch-roll rotations are uniformly excited.

Intel D435i integrated with camera and IMU (Bosch) are fixed to the 6th joint. The monocular camera samples the image at 20 fps; its image resolution is 640×480. The camera intrinsic parameters are calibrated with standard deviation less than 0.1 pixel. The IMU samples the inertial measurements at 200 Hz. The inertial noise terms are estimated using Allan variance analysis [45]. The initial acceleration noise and its bias noise are 0.00014 m/s2and 0.00004 m/s3respectively;gyroscopic noise and its bias noise are 0.00035 rad/s and 0.000055 rad/s2, respectively. The image and inertial data,together with robot poses, are synchronized by timestamps.The calibration parameters are calculated on the laptop with 2.4 GHz Intel Core i7 and 8 G RAM.

B. Repeatability Test

Since the poses read from the robot arm are used to define the trajectory for calibration consistency, we firstly test the robot moving repeatability. The robot is programmed to follow a pre-defined trajectory and expected to move and return to the same set of fixed points. Also, the positions and orientations read from the robot are supposed to be precise.The robotic arm is tested by automatically moving its end to a set of specified spots on a calibration table. A 10×10 chessboard points are designed; each point is denoted by a 1×1 millimeter square. The robot goes over the chessboard points cyclically for more than 100 times. It has been found that the robot arm always directs to the grid points with position error less than 0.1 mm and rotation error less than 0.2°. Hence, the robot moving repeatability satisfies our requirement.

C. Designed Trajectory

In the test, we use Apriltag [51] as the calibration board.The robotic arm with the joint-mounted monocular camera and IMU moves in front of the calibration board to capture the Apriltag patterns in the image sequence. It is noticeable that the moving trajectory proceeds in a spiral fashion, as shown in Fig. 4. The trajectory projections onx-yplane,x-zplane, andy-zplane are shown in Fig. 5, Fig. 6, Fig. 7, respectively. This type of trajectory is intentionally designed to fully and uniformly excite yaw-pitch-roll rotations andx-y-ztranslations. Besides, in order to satisfy that the calibration tag patterns are captured in the image sequence, the poses are supposed to enable camera lens (optical axis denoted by blue axis in Fig. 4) point to the calibration board.

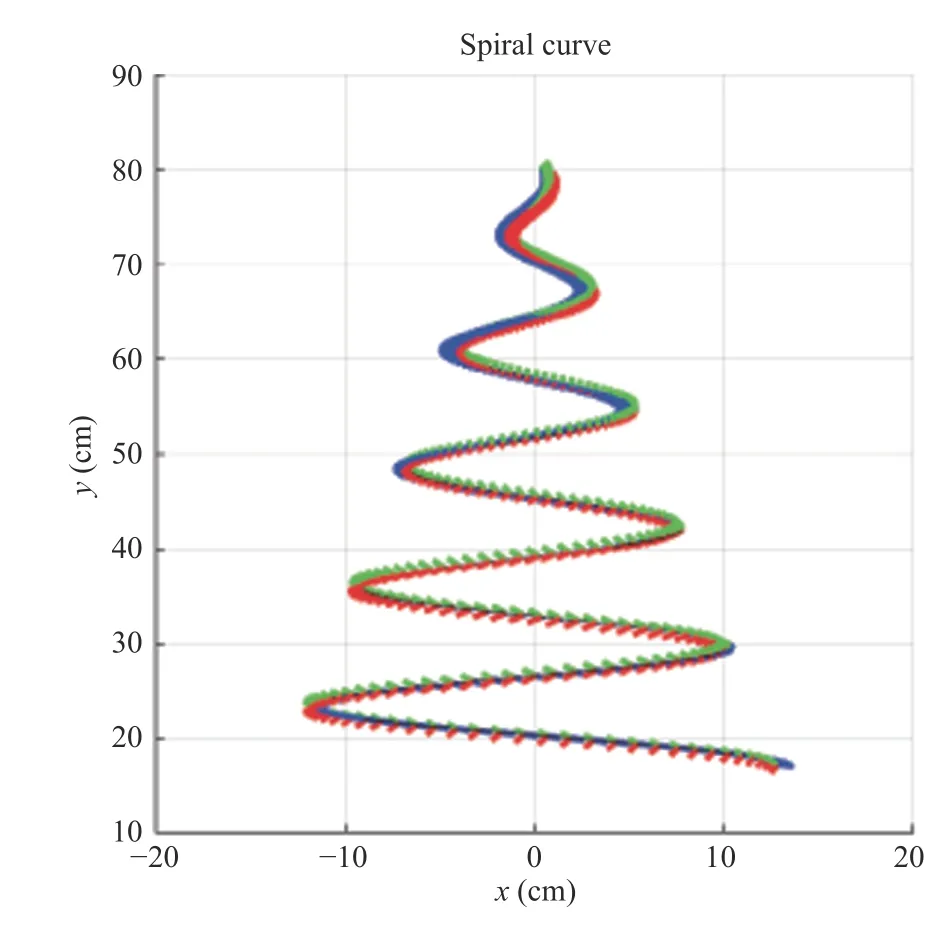
Fig. 5. Manipulator trajectory projected onto x-y plane.

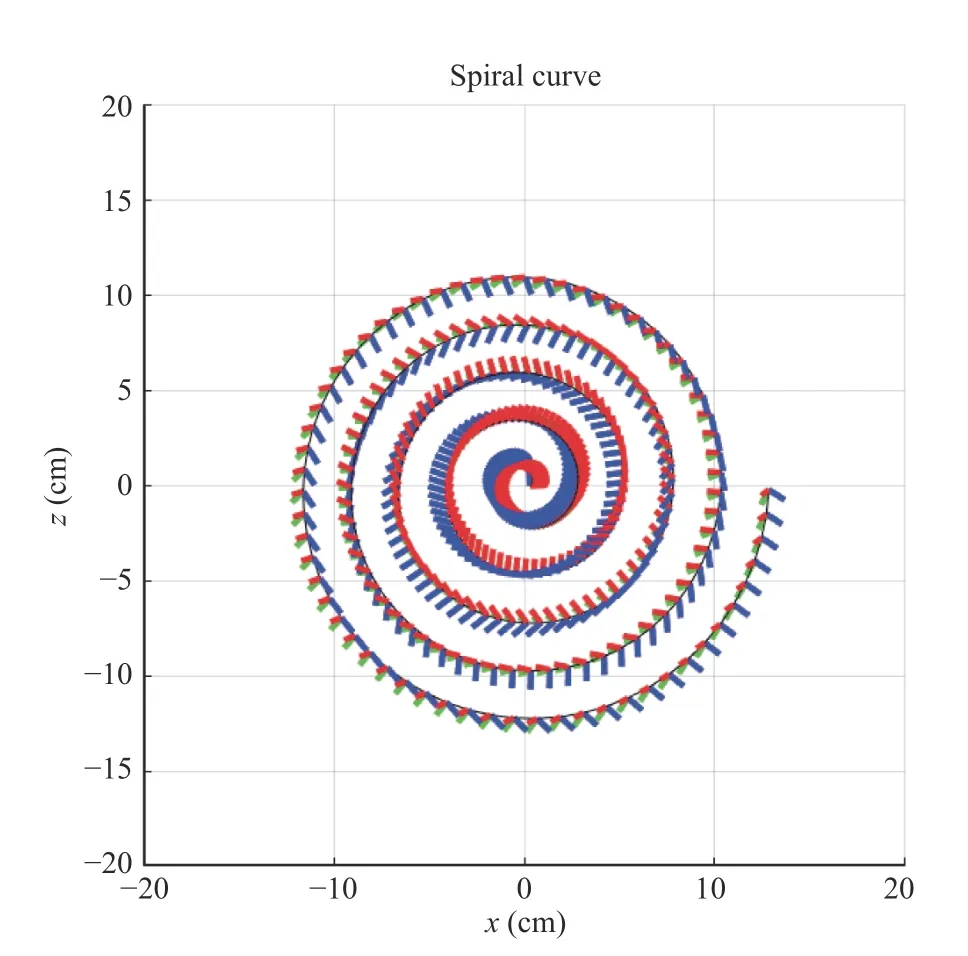
Fig. 6. Manipulator trajectory projected onto x-z plane.

Fig. 7. Manipulator trajectory projected onto y-z plane.

The robot spiral moving pattern is

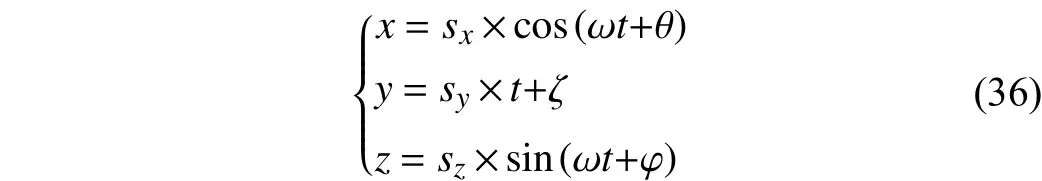
wheresx=0.3,sy=−2, andsz=0.3 denote the moving scale along the axes; ω=1 is the angular rate; θ=1, ζ=80, and φ=1 are the initial phases.

The correspondingyaw-pitch-rollangles are parameterized by

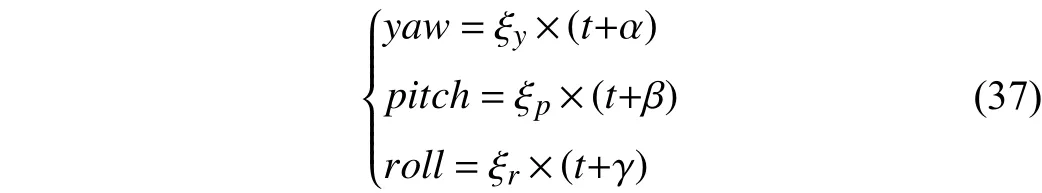
where ξy=0.001, ξp=0.01, and ξr=0.001 are the angular scales onyaw,pitch, androll, respectively; α=2, β=−1, and γ=1 are the initial angular phases, respectively.

In robot cartesian mode, there are some configurations in which the robot loses one or more degrees of freedom (i.e., the robot is unable to move in one direction or another). In order to maximally reduce the odds of singularity, we used the

ActivateAutomaticSingularityAvoidanceAPI function and set it to false. However, it should be noticed that the designed moving trajectory might still be affected due to the existence of singular positions inside the robot workspace, while calculating its inverse kinematics using ROS Moveit [52]. In presence of singularity, the robotic arm will move arbitrarily or stay still (For instance, the arm is at full reach. It is unable to move anymore in the direction it is currently reaching out),rather than proceed in the predefined path. In order to solve this issue, we have tried several initial poses and enabled the robot arm to move the predefined spiral trajectory.Afterwards, the initial pose and its corresponding trajectory without any singularities during the moving process are selected. Additionally, the joint moving angle series are computed in advance, which could save computational time for deriving inverse kinematics during the movement. Totally,there are 80 poses during the manipulator movement. The robot followed the spiral trajectory and the whole movement process lasted about 2 minutes. It has been repeated 20 times for the spiral curve trajectory. The computational time for each trajectory was approximately 10 minutes.

The translations for the designed trajectory are shown in Fig. 8. The translations onxandzaxes (scale:[−12.85 cm,12.85 cm]) are designed to proceed in a sinusoidal form. The translation onyaxis proceeds in a dog-leg path(scale: [17.20 cm,80.00 cm]). The moving pattern moves back and forth for a few times.

The moving trajectory angular curves are shown in Fig. 9.For ensuring the cameray-axis points approximately to the calibration board, we designed theroll(angle scale:[0°,17.76°]) andyaw(angle scale: [28.71°,46.47°]) that move in a relatively small scale. Comparably, thepitch(angle scale:[2.23°,233.14°]) alongy-axis changes in a dog-leg style on a large scale.

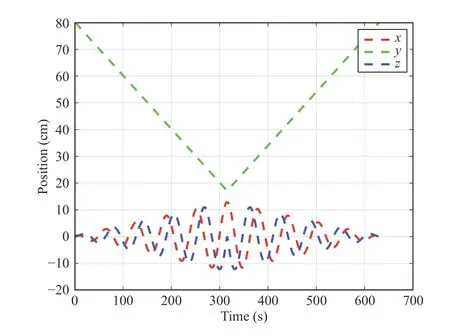
Fig. 8. Trajectory curves with repsect to x, y, and z.

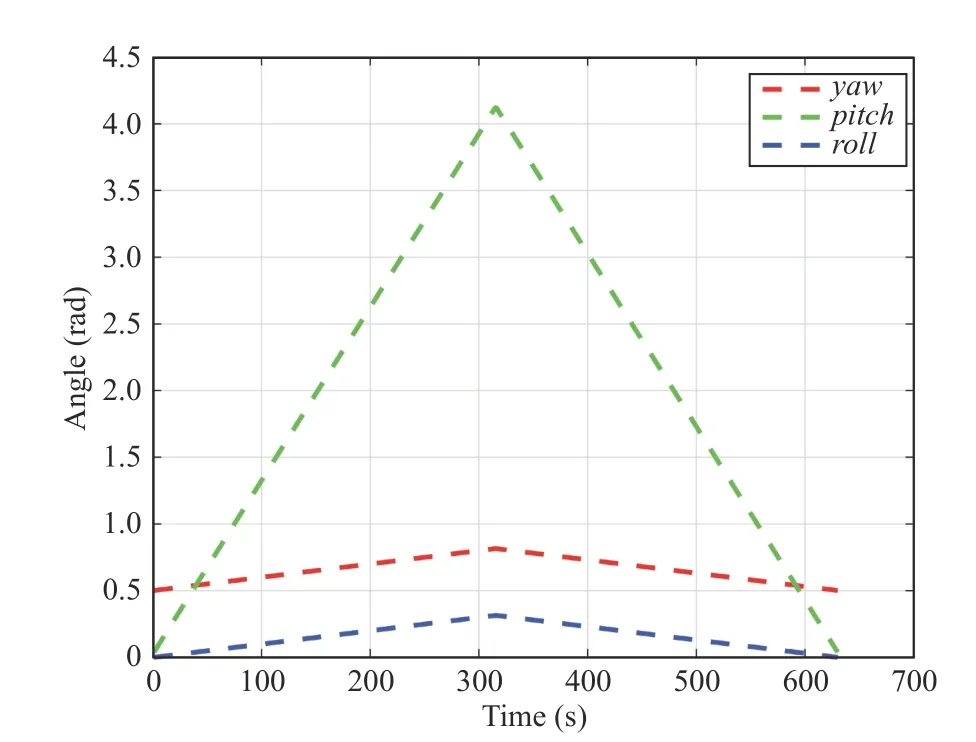
Fig. 9. Trajectory curves with respect to yaw-pitch-roll.

D. Results and Analysis

In our experiments, more than twenty groups of visualinertial and robot pose data were collected. Each test lasted about 60 seconds. The acceleration biases are [0.105 m/s−2,−0.131 m/s−2,−0.065 m/s−2]; the gyroscopic biases are[−0.0068 rad/s,−0.0008 rad/s,0.0014 rad/s].

Our method has been compared with state-of-the-art, i.e.,ICSR [53] and Kalibr [25]. The designed trajectories for the traditional calibrations include the typical motions, e.g.,circular motion, zig-zag motion, circular motion, rosette motion and irregular rotation & translation that excite 6DOF motions. The tests have been repeated more than 20 times.

In Fig. 10, it can be observed that ours achieves more stable and consistent outcomes (obviously smaller standard deviations onx-y-ztranslations andyaw-pitch-rollrotations) than the other two methods, partly because the geometrical constraint among camera, IMU and robotic arm is added to the calibration model. Also, the robotic arm moves in a predefined spiral fashion, which could potentially improve moving consistency, accuracy, stability.

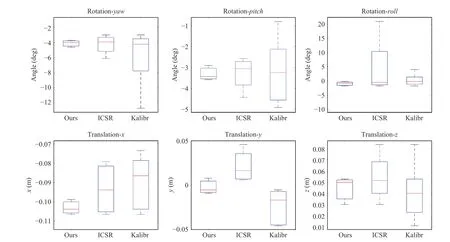
Fig. 10. Comparisons on calibration methods using Ours, ICSR [53], and Kalibr [25]. It includes the comparisons on rotation: yaw, pitch, roll; and translations: x, y, z.

Fig. 11. Comparisons on image reprojection error between (a) Ours, (b) ICSR [53], and (c) Kalibr [25].

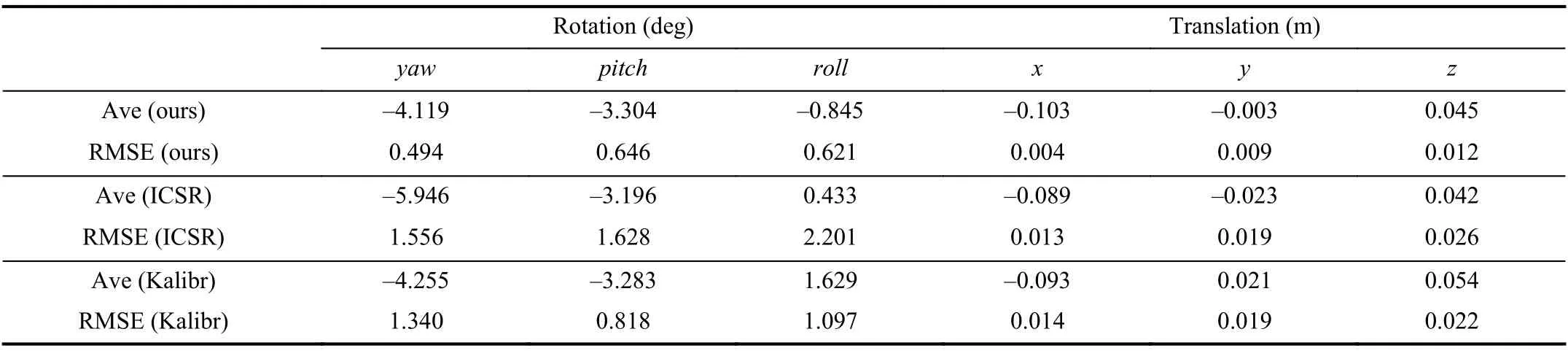
TABLE II COMPARISONS OF CALIBRATION METHODS BETWEEN OURS, ICSR, AND KALIBR

The corresponding Average and root mean squared error(RMSE) of translations and rotations are shown in Table II. Its Std onyaw,pitch,rollare 0.494°, 0.646°, 0.621°; its translation Std onx,y,zare 0.004 m, 0.009 m , and 0.012 m,respectively. From the results, we can see that ours achieves competitive results while comparing with the other two methods in terms of both Average and RMSE.

The reprojection errors are also analyzed and compared.As shown in Fig. 11(a), most of the reprojection errors are within the circle less than 0.25 pixel. Comparably, the convergence area using ICSR [53] (Fig. 11(b)) and Kalibr [25](Fig. 11(c)) are relatively larger, which are approximately 0.5 pixel.

Fig. 12. Comparisons on acceleration errors and angular velocity errors using ours, ICSR, and Kalibr. (a)–(c) Acceleration errors in 2d; (d)–(f) Gyroscopic errors in 2d; (g)–(i) Acceleration errors in 3d; (j)–(l) Gyroscopic errors in 3d.

We have also compared the acceleration errors and angular velocity errors in both 2d and 3d forms. As can be seen in Figs. 12(a)–12(f), the acceleration and angular velocity errors are all within a small range. By contrast, there exist severe error jitters for both ICSR and Kalibr, which can be attributed to unexpected disturbances and manual jitters during the movement. In Figs. 12(g)–12(i), the acceleration errors are plotted in its 3d form. The acceleration convergence sphere radius using our method is approximately 0.429 m/s2; while the other sphere radii are roughly 1 m/s2. In a similar manner,the gyroscopic errors are plotted in Figs. 12(j)–12(l), the convergence area radius of our method is 0 .08 rad/s, while the radii for ICSR and Kalibr are 0.107 rad/s and 0.114 rad/s,respectively. From the results, it can be observed that IMU errors are comparably smaller than the state-of-the-art, thanks to the spiral moving trajectory design and decoupled estimations on translation & rotation.

We have also performed the comparisons on the computational time between ours, ICSR [53], and Kalibr [25],to evaluate the method efficiency. As can be observed in Table III, the spiral moving trajectory has been performed two times. The collected dataset related to the first test has approximately 2400 images and the capturing sequence lasts about 120 seconds; the dataset related to the second test has approximately 3600 images and the capturing sequence lasts about 180 seconds. The symbol “*” represents the IMU preintegration. From the results, it can be seen that the computational time using ours with IMU preintegration takes 1232 seconds (the the least amount of time), which can be largely attributed to the strategy in the inertial preintegrated process. IMU preintegration saves the time in iterations of quaternions, which are fed into the velocity and position model. Comparably, ours without preintegration consumes longer time in deriving the calibration parameters. It can be observed that ICSR and Ours show comparable computational time, but ours achieves higher calibration accuracy.Noticeably, Kalibr requires large amount of time, especially for the one with a larger dataset, which is due to the minimization of bundle volume of states being processed.

TABLE III COMPARISONS ON THE COMPUTATIONAL TIME BETWEEN OURS (WITH IMU PREINTEGRATION), OURS (WITHOUT IMU PREINTEGRATION), ICSR [53], AND KALIBR [25] USING THE SPIRAL MOVING TRAJECTORY. THE 1ST TEST SET HAS APPROXIMATELY 2400 IMAGES AND THE CAPTURING SEQUENCE LASTS ABOUT 120 SECONDS. THE 2ND TEST SET HAS APPROXIMATELY 3600 IMAGES AND THE CAPTURING SEQUENCE LASTS ABOUT 180 SECONDS. “*”MEANS THE IMU PREINTEGRATION

VI. CONCLUSION AND FUTURE WORK

In this paper, we have developed a unifying monocular visual-inertial and robotic arm calibration framework. It is able to geometrically correlate the spatial relationship among the sensing unit and robotic arm. Besides, we have designed the calibration moving trajectory in a spiral pattern. Through this design, the excitations onyaw-pitch-rollrotations andx-yztranslations could be performed uniformly and consistently.The performance of the calibration has been evaluated on our developed platform. In the experiments, the standard deviations on rotations and translations are less than 0.7°and 0.012 m, respectively, which proves its advantages in visualinertial-robot calibrations.

One drawback of our current calibration method is the lack of systematic comparisons on the typical trajectories, such as zig-zag trajectory, circular trajectory, radial trajectory, rosette trajectory. Thus, in the future, we plan to perform more tests and analysis on these trajectories. Besides, we will perform the robot calibration based on [38] to check the repeatability and accuracy of the manipulator qualitatively. Eventually, we plan to design that trajectory that could avoid singularities in the robot cartesian space since the robot experiences the inevitable singularity in the moving process.