基于深度学习的“勾股定理的应用”课堂设计

⦿青岛经济技术开发区第四中学 孔祥骞

所谓深度学习，是指在教师引领下，学生围绕着具有挑战性的学习主题，全身心积极参与、体验成功、获得发展的有意义的学习过程[1].深度学习是改变传统的一言堂、满堂灌，突出学生为主体，侧重思维发展的新型学习方式.下面就基于深度学习的一节课的课堂设计展开讨论.

1 教学分析

1.1 教材分析

本节是人教版八年级数学下册第17章第二节的内容，主要是在前面已学过探究和证明勾股定理的基础上对勾股定理进行简单的应用.

1.2 教学目标

根据教材内容及学情，对本节课制定以下教学目标：

(1)经历将实际问题转化为直角三角形模型的过程，能用勾股定理解决问题，发展应用意识；

(2)在解决实际问题的过程中，体验解决问题的策略，养成独立思考和质疑的习惯.

2 教学过程

2.1 情境设置

首先回顾勾股定理的主要内容：

师：上一节，我们已经学习了直角三角形中三条边的关系，请大家回忆勾股定理的主要内容.

生：在直角三角形中，两条直角边的平方和等于第三条边的平方.

师：请同学们尝试用勾股定理解决下面的问题.

课件呈现：

(1)求图1所示的直角三角形的斜边AB的长度；

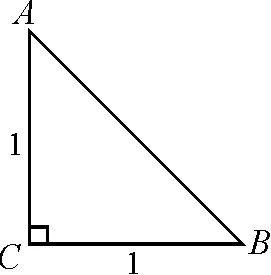
图1

(2)求图2所示的Rt△ABC中BC的长度；

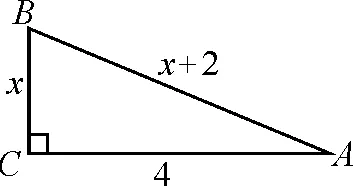
图2

(3)求图3所示的等腰三角形底边BC上的高.

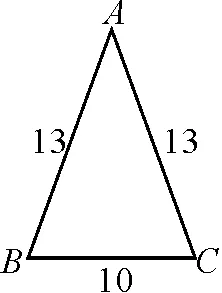
图3

小组内讨论并思考：在解决问题时，(1)(2)(3)三者之间的异同点.

小组A：都需要用勾股定理去解决.

师：非常好，找到了解决问题的关键点.那三个问题解决方法一样吗？

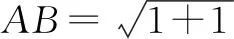
师：说得非常准确，理解也非常透彻！本节课我们就利用勾股定理直接求解，已知直角三角形某两边关系列方程求解和没有直角三角形构造直角三角形求解这三种情况开始学习.

设计意图：利用三个简单的基本三角形简洁明了地展示了本节课的整体的设计脉络，同时为学生利用勾股定理解决实际问题打开了思路，初步获得解题经验，有利于学生更深刻地理解勾股定理的应用.小组讨论有利于学生思维的碰撞，提高合作意识，共同进步.

2.2 问题驱动

模块一：直接应用，巩固定理

教师出示问题：

在一次台风的袭击中，小明家房前的一棵大树在离地面6 m处断裂，树的顶部落在离树根底部8 m处，如图4.你能告诉小明这棵树折断之前有多高吗？

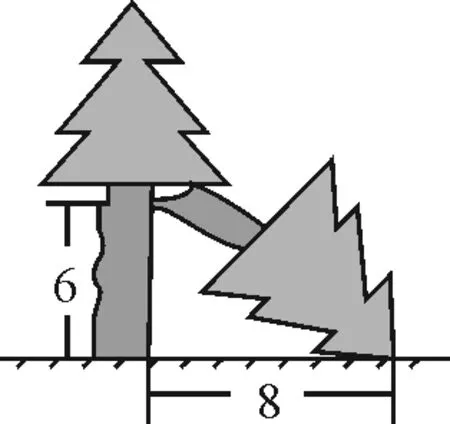
图4

生：由勾股定理可得树原来有16 m.

师：你是如何得出的？

生：可以抽象出一个直角三角形，且两直角边分别为6 m和8 m，类似图1，由勾股定理直接求折断部分的长，然后与下半部分加起来即原树高.

设计意图：本模块的设置正是前面情境设置中的第(1)题的变式，赋予实际背景之后，学生只需将实际问题抽象成数学图形，进而解决.这里不仅要求学生对勾股定理透彻理解，还需要具有将实际图形转化为数学图形的能力.

模块二： 变换条件，探究变化

如果变换条件，得到如下问题：

在一次台风的袭击中，小明家房前的一棵16 m的大树被风刮断，如图5，树的顶部落在离树根底部8 m处.你能告诉小明这棵树是在多高处折断的吗？

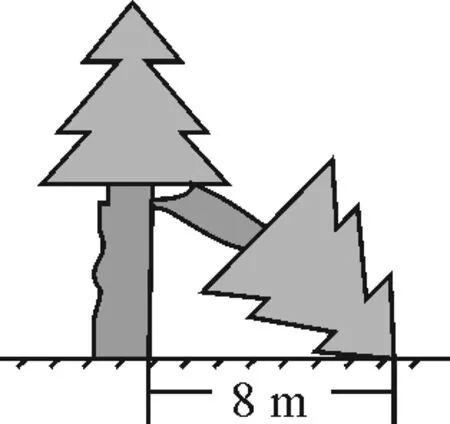
图5

师：请同学们先自己思考，再小组内交流，最后以小组为单位解决问题.

小组C：先由实际图形抽象出一个直角三角形，由已知条件可得，一条直角边边长为8，另外两边都不知道，但是知道它们两个的和为16.可以设另一条直角边边长为x，那么斜边长就可以用16-x来表示，应用勾股定理可得x2+82=(16-x)2，解出x即可.

师：这一问题变化在哪？

生：与图2对应的问题类似，已知直角三角形中确定一条边以及另外两条边的关系，可以依据勾股定理列方程求解.

设计意图：本模块在模块一的基础上条件稍作改变，依据情境设置中第(2)问的解题思路去解决，加深学生对勾股定理的理解，发展学生的方程思想.

模块三：巩固提升，深度学习

师：如图6，在模块一、二问题的基础上，树干A处有一知了，大树折断落地后同时从离地面3 m高的位置落到地面，且距离树的的顶部4 m，你能求出知了原来在树的多高处吗？

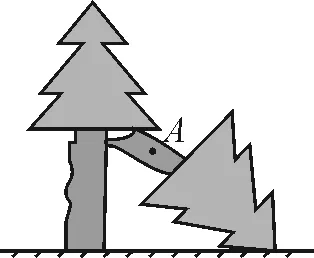
图6

要利用勾股定理解决此问题，需要找出所在的直角三角形，那么利用前面构建的直角三角形可以解决吗？需要将这一问题放在哪个直角三角形中呢？

学生：可以考虑从A处向地面做一条垂线段AB，构造出一个直角三角形.如图7，在Rt△ABC中，两直角边分别为3和4，由勾股定理可得斜边为5 m.也就是说知了离树的顶端5 m，所以知了在树的11 m高处.

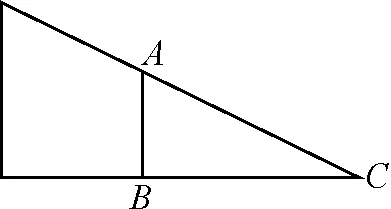
图7

设计意图：基于模块一和模块二的实际背景，继续探讨没有直角三角形时，如何构造直角三角形去解决问题.

2.3 迁移应用

(1)如图8，长方形ABCD中 ，AB=3,AD=1,AB在数轴上，若以点A为圆心，对角线AC的长为半径作弧，交数轴的正半轴于点M，则点M表示的数为________.

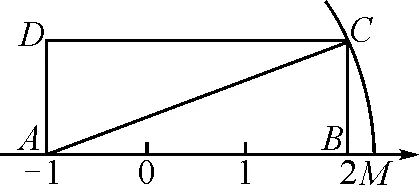
图8

(2)如图9，印度数学家什迦逻(1141-1225)曾提出过“荷花问题”：“平平湖水清可鉴，面上半尺生红莲；出泥不染亭亭立，忽被强风吹一边；渔人观看忙向前，花离原位二尺远；能算诸君请解题，湖水如何知深浅？”请用学过的数学知识回答这个问题.

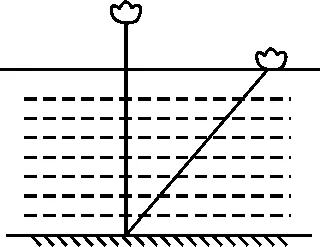
图9

(3)如图10，有两棵树，一棵高12 m，另一棵高6 m，两树相距8 m.一只鸟从一棵树的树梢飞到另一棵树的树梢，则小鸟至少飞行______m.

图10

小结：今天你有哪些收获？

设计意图：在前面三类问题的基础上设置同样类型的题目进行练习，加以巩固，最后小结，学生针对不同类型题目总结出不同解题策略，加强对勾股定理的应用的学习深度.

3 设计思考

3.1 提炼模型，理解本质

“勾股定理的应用”这一节先用三个有层次的简单问题(知道直角三角形的两边，直接利用勾股定理计算第三边；已知直角三角形中一条边和另两条的关系，利用勾股定理列方程计算；没有直角三角形需构造直角三角形)调动学生思考、探究的积极性，引导学生体会不同问题的解题方法，提升学生的思维能力，并积累解题经验，形成解题思路，为本节课的学习奠定基础.

3.2设计变式，分析模型

教学过程中的三个模块是在同一个实际背景下分别对应情境设置中三个模型进行的变式，由浅入深，逐层递进.在经历了情境设置中的三个问题后，学生已经有了解题思路，但需要深度加工，抽象出几何图形；同时，变式也促进了学生的深度学习.

3.3 渗透思想，提升能力

在变式中，学生进一步深刻理解三类问题的解题方法，随堂练习更是加深了学生对本节课的思想方法的理解.通过不断地对知识归纳总结，并对所学知识有新的认识，进一步达到深度学习.

4 写在最后

深度学习是理解性的教学，不是灌输性的教学；是反思性的教学，不是接受性的教学[2].深度学习是追求提升学科内涵、发展学科核心素养的教学.

深度学习的教学设计是建立在学生原有的认知结构上，以学生为主体的设计.若不能深入地开展教学，只能认为是教师一堂精彩的自我表演.因此，双减教育形势下，教学设计要考虑本节课的目标是什么，重难点是什么，应当采用什么样的教学手段让学生构建新的知识体系.在教学过程中，教师应该研究知识本质，深挖知识点之间的联系，尽量将知识点进行有机整合，促进学生的深度学习[3].

苏格拉底说:“教育不是灌输,而是点燃火焰.”深度学习就是点燃学生、点燃课堂的火焰.期待深度学习的星星火焰，在数学课堂上日渐燎原.