规律源自猜想 精彩源于变式 素养成于实践
——以“两条直线成为折线型平行线的条件”教学为例
2022-10-26广州市骏景中学顾桂新
⦿广州市骏景中学 顾桂新
《义务教育数学课程标准》指出:学生通过义务教育阶段的学习,经历观察、实验、猜想、证明等数学活动,发展合情推理能力.猜想是获得规律的方法,在观察中获得的特殊例子放到一般情况下看看是否也有这种可能性,即从特殊到一般.一题多解的变式教学可以激发学生的学习兴趣和求知欲,向学生展示不同的思考过程,根据学生的最近发展区适当地拓展解题思路,从而让学生主动学习,实现有意义地建构,也能使不同层次学生的数学思维能力都得到提高,这是数学教学中十分重要的一环.基于此,笔者根据人教版七年级下册数学,执教了“两条直线成为折线型平行线的条件”,从“特殊到一般”“一题多解”上下功夫,收获良多.
1 从特殊到一般,以旧引新,大胆猜想,导出主题
学生已经学习过“平行线的判定方法”“平行线的性质定理”等知识,明确“角的数量关系”与“两直线位置关系(平行)”之间是可以互推的.如何从这些旧知识出发,使学生想到,“两条直线成为折线型平行线的条件”呢?
问题1我们知道平行线判定方法有四种.如图1,AB,CD被BD所截,∠B,∠D满足什么数量关系时,AB∥CD?

图1
设计意图:通过动态改变AB的位置,明确“∠B+∠D=180°”与“两直线平行”可以互推,唤醒学生的知识储备.
问题2如图2,当点O在线段BD上运动时,猜一猜:若AB∥CD,则∠B+∠D与∠BOD须满足什么数量关系?

图2
设计意图:通过增加点O,在两个同旁内角基础上增加了一个平角.当∠B+∠D=180°时,AB∥CD;而∠BOD=180°.从而引导学生得到当点O在线段BD上移动时,∠B+∠D与∠BOD须满足某个数量关系,AB,CD方可以成为平行线.
问题3当点O从线段BD上移动到平面内任意位置,即变成折线型时,不妨研究点O向左移动时的情况.如图3,猜一猜:∠B,∠D,∠BOD须满足什么数量关系,才有AB∥CD?
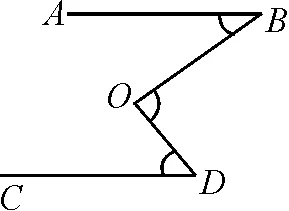
图3
设计意图:在问题2的基础上引出本节课主题“两条直线成为折线型平行线的条件”,同时通过问题2的特殊情况,引导学生从“特殊到一般”探究规律的过程中,通过观察,猜想三个角之间满足什么数量关系,两条直线能成为“折线型”平行线.
在问题3中,学生猜想三个角之间满足∠B+∠D=∠BOD时,AB∥CD,即为两条直线成为“折线型”平行线的条件.接下来证明猜想的正确性.
2 一题多解,突出思维之道
证明两条直线平行的方法有多种,通常从“三线八角”的基本图形中寻找同位角、内错角、同旁内角等,运用平行公理或平行线判定定理解决.若没有现成的“三线八角”,就需要构造,这是初中数学学习的难点.
问题4问题3猜想的证明如何通过添加辅助线来构造“三线八角”,找出解题路径呢?
设计意图:教师先引导学生构造同旁内角互补,证明两直线平行,证法1作为例题加以讲解;然后学生模仿证法1,由平行线的判定方法,从内错角相等、同位角相等、平行公理等角度思考,添加辅助线解决问题.证法2~5是学生提出来的各种解法.
证法1:如图4,连接BD,构造同旁内角互补,证明两直线平行.

图4
在△BOD中,∠2+∠3+∠BOD=180°.
又∵∠BOD=∠1+∠4,
∴∠2+∠3+∠1+∠4=180°.
∴∠ABD+∠BDC=180°.
∴AB∥CD.
证法2:如图5,延长BO,与CD交于点E,构造内错角相等,证明两直线平行.
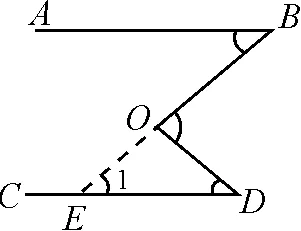
图5
在△OED中,∠1+∠D=180°-∠DOE.
又∠BOD=180°-∠DOE,
∴∠1+∠D=∠BOD.
∵∠BOD=∠B+∠D,
∴∠1+∠D=∠B+∠D,即∠1=∠B.
∴AB∥CD.
证法3:如图6,过点O作直线a∥AB,从平行公理的角度思考,构造中间量,由直线a∥AB知∠1=∠B.

图6
∵∠BOD=∠1+∠2,
∠BOD=∠B+∠D.
∴∠1+∠2=∠B+∠D.
∴∠2=∠D.
∴a∥CD.
∴AB∥CD.
证法4:从将∠BOD拆解成两个小角的角度思考.如图7,作∠BOE=∠B,则OE∥AB.
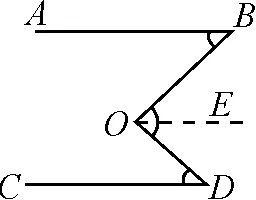
图7
∵∠BOD=∠BOE+∠DOE,∠BOD=∠B+∠D,
∴∠BOE+∠DOE=∠B+∠D.
∴∠DOE=∠D.
∴OE∥CD,
∴AB∥CD.
证法5:构造垂直,将AB,CD直接联系起来.如图8,过点O作AB的垂线,交AB于点E,交CD于点F,则∠BEO=90°,且∠1+∠B=90°.

图8
∵∠1+∠2+∠BOD=180°,∠BOD=∠B+∠D,
∴∠1+∠2+∠B+∠D=180°.
∴∠2+∠D+90°=180°.
∴∠2+∠D=90°.
∴∠OFD=90°.
∴∠OFD+∠BEO=180°.
∴AB∥CD.
上述证法是学生通过猜测、尝试,在教师指导下得出的证明方法.通过一题多解,启发学生基于原有经验,突破思维局限,创新探究思路,完成探索推理,概括获得新知;通过一题多解,培养学生积极思考,勇于尝试的精神.
3 归纳共性,揭示问题本质规律,触类旁通
通过对问题3猜想的五种证法的学习,发现除了证法1外,其他的方法都是以点O为切入点,也就是所作的辅助线都与点O有关系,如过点O作平行、延长BO、过点O作垂直等,其目的是依据现有的图形通过作辅助线,构造“三线八角”和三角形这两种基本图形,从而根据“三线八角”角度之间的数量关系与三角形内角和为180°进行等量代换,得到角的关系,最终证明两直线平行,这是该研究的根本所在.
问题5刚才研究了点O向左运动的情况,那么当点O在平面内向其他方向运动时,还可以得到哪些不同的新图形呢?对每种新图形,∠B,∠D,∠BOD满足什么数量关系时,AB∥CD?请证明你的猜想.
设计意图:学生通过动手作图、试验,得到不同类型的两条直线成为折线型平行线的图形.如图9所示,点O可以向右运动,向左上运动,向右上运动,等等.对于每一种图形结论的猜想与证明,引导学生在课后根据自己的选择,选取自己喜欢的方法完成,并体会运动变化中不变的规律.
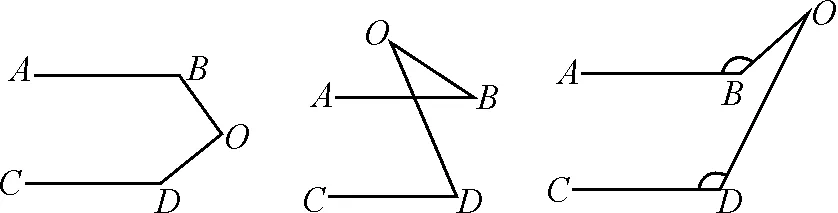
图9
4 结语
变式教学即通过不断改变问题情境、问题条件,探索变化规律以及变化中的不变性质.在整个教与学的活动过程中,学生既要参与解题,更要参与数学思考,在思考的过程中去体会“变”与“不变”的辩证思想,体验数学创造、数学探究与数学发现的过程.
通过变式教学,不仅改变了学生被动的学习方式,也大大开阔了教师的解题视野.教师不必再停留在繁忙的找题、做题、讲题的题海战术之中,而是可以更好地利用经典试题进行深度剖析,充分演变,揭示问题的本质规律,达成举一反三、触类旁通的教学效果.
本节变式教学课,从特殊到一般,给学生创造观察、探究、猜想、归纳等学习机会,引导学生“从事物的具体背景中抽象出一般规律和结构”,让学生在活动中增强求知欲,凸显学生学习的主体地位,克服学习中的思维定式.通过“一题多解”的变式教学,向学生展示不同的思考过程,根据学生的最近发展区适当地拓展解题思路,从而让学生主动学习,实现有意义地建构,也能使不同层次学生的数学思维能力都能得到提高,这是数学教学中十分重要的一环.
