老岚水库土石坝渗流数值模拟研究

岳庆河，郭清华，张大雷

(烟台市城市水源工程运行维护心，山东 烟台 264000)

老岚水库枢纽工程坝型为混凝土重力坝与黏土心墙土石坝结合的混合坝，使用ANSYS有限元分析软件APDL语言编写程序对软件进行功能扩充，得到土石坝渗流场有限元分析程序，可以方便快捷地进行渗流数值模拟分析，研究老岚水库土石坝渗流特性，为渗流控制提供参考。

1 工程概况

老岚水库坝址位于烟台市福山区外夹河中游，控制流域面积624km2，总库容15792m3，兴利水位44.8m，兴利库容8491万m3，死水位34m，死库容513万m3，属大(2)型水库，枢纽工程于2020年10月开工，计划2023年具备蓄水条件。工程建设任务以城市供水、防洪为主，兼顾灌溉和改善下游生态环境等综合利用。坝址区属丘陵河谷地貌，呈不对称的宽U形河谷，两岸坝肩地形起伏不大，边坡岩体主要为花岗斑岩和二长花岗岩。坝型为混凝土重力坝与黏土心墙坝结合的混合坝，重力坝段布置于左岸及主河槽，黏土心墙坝段布置于右岸。黏土心墙砂壳坝坝顶高程50.5m，坝顶长439m，坝顶宽度8m，最大坝高27.5m，黏土心墙顶高程48.5m，顶宽3m，如图1所示。

2 渗流程序开发

2.1 开发基础

ANSYS提供了APDL参数化设计语言，允许用户开发专用有限元分析程序，扩展了ANSYS使用范围，二次开发渗流分析程序可充分利用ANSYS可视化的前后处理能力，方便了建模、模型检察、结果查看及对结果的计算分析，避免了重复编制有限元程序的繁锁[1]。通过对比分析，渗流场与温度场的热传导都遵循质量(或能量)守恒定律，渗流微分方程与热传导微分方程形式完全相同，参数及边界条件相互对应，为应用ANSYS热传导模块二次开发渗流场分析程序奠定了基础[2- 5]。

不考虑土骨架变形及水压缩性时，饱和—非饱和渗流微分控制方程为：

(1)

以温度T为控制变量的热传导微分方程为：

(2)

式中，λx、λy—x、y方向的热传导系数，W/(m·℃)；c′—比热系数，J/(kg·℃)；ρ—介质密度，kg/m3。

图1 桩号0+325处土石坝剖面图

2.2 程序结构

渗流计算时非饱和土渗透系数、浸润线位置、逸出面边界条件等需在计算过程中迭代确定[6- 7]。程序设计为两层迭代结构，内层迭代确定非饱和土渗透系数，计算时保持边界条件不变，渗透系数根据单元孔隙水压力不断调整，直到前后2次计算各单元孔压变化差小于某一定值时计算收敛；外层迭代确定渗流逸出点位置，调整逸出面边界条件范围，渗流向外流通时计算收敛。完成计算后，利用ANSYS后处理模块可以直观的查看浸润线位置、渗透比降、逸出点位置等信息，通过对下游坡节点热流通量求和得到单宽渗漏量值。二次开发的渗流程序框图如图2所示。

图2 渗流计算迭代程序框图

3 渗流计算

3.1 网格划分及渗透系数确定

在ANSYS中采用PLANE55单元，坝体部位取0.2m、坝基取0.5m进行网格划分，共划分119433个单元，239940个节点，坝体筑坝材料和坝基饱和渗透系数见表1。

表1 各土层饱和渗透系数

非饱和土相对渗透系数采用Van Genuchten-Mualem公式确定[8]。

(3)

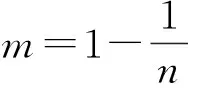
3.2 不同上下游水位工况计算

计算3种设计工况，分别为：①上游兴利水位44.8m、下游相应最低水位32.4m；②上游设计洪水位46.27m、下游相应水位34.82m；③上游校核洪水位48.35m、下游相应水位36.88m。为了对比分析，增加2种假设工况，分别为：④上游校核洪水位48.35m，下游水位34.82；⑤上游校核洪水位48.35m，下游水位32.4。列出了部分计算图形如图3—6所示，求得关键部位渗流要素见表2。

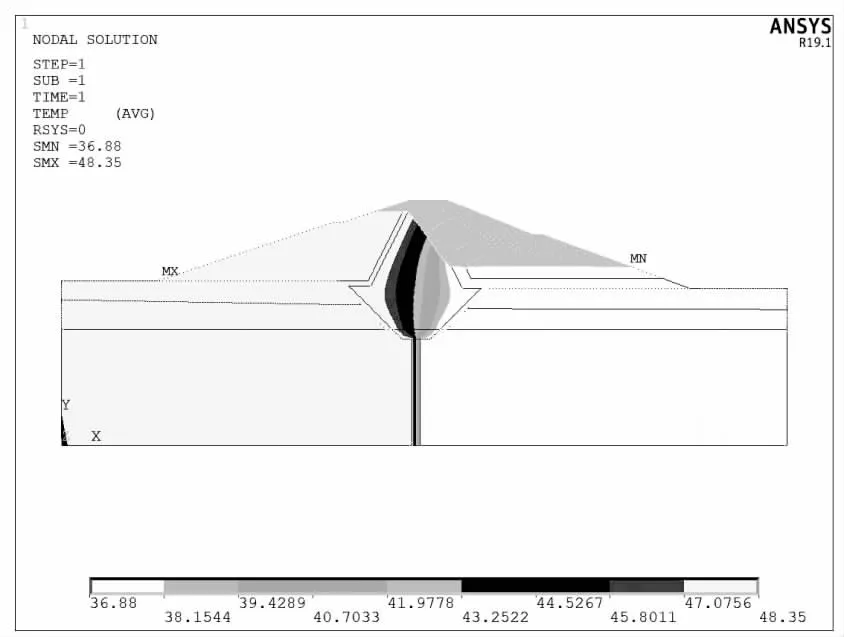
图3 工况③总水头等值线图

图4 工况③孔隙水压力等值线图

图5 工况③下游坡渗透比降图

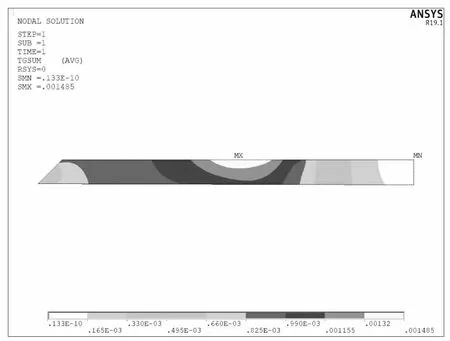
图6 工况③坝基中粗砂层渗透比降图

表2 不同水位组合下关键部位渗流要素表

3.3 假设不利工况计算

渗漏问题是导致土石坝溃坝事件的重要原因，假设土石坝可能引发渗漏问题的不利工况，研究其对渗流场变化影响[9- 10]。在工况②的基础上，分别假设防渗帷幕防渗效果差(调整帷幕渗透系数为1×10-7m/s)得到工况⑥、心墙及截水槽防渗效果差(调整心墙渗透系数为2.9×10-7m/s)得到工况⑦、反滤排水体失效(调整反滤排水体渗透系数为3.5×10-5m/s)得到工况⑧。列出了部分计算图形如图7—8所示，求得关键部位渗流水力要素见表3。

图7 工况⑥总水头等值线图

表3 假设不利工况下关键部位渗流水力要素表

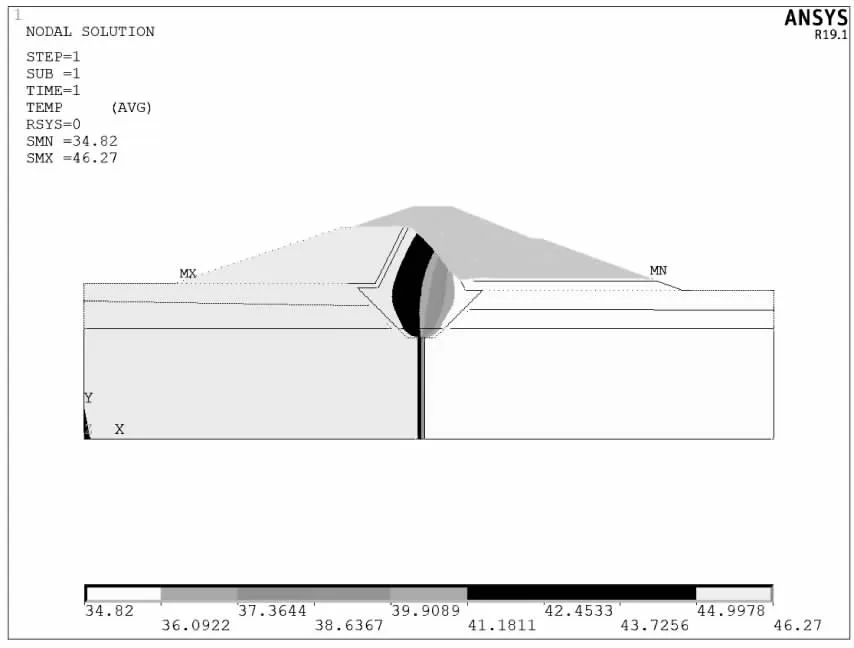
图8 工况⑦总水头等值线图

4 成果分析

(1)各种工况下游坝坡浸润线均与下游水位平齐，黏土心墙降低浸润线高度效果显著，出逸点位置均在下游水位线处，无自由出逸面；根据地质勘查成果，坝壳砂砾料允许渗透比降0.45、坝基粗砂层允许渗透比降0.22，出逸点及坝基砂渗透比降均未超过允许值。

(2)渗透比降大值集中在心墙及防渗帷幕中，坝壳砂料及坝基其它区域渗透比降较小；下游坝坡渗透比降最大点发生在出逸点位置，坝基砂层渗透比降最大点发生在坝坡与坝基接触点处。

(3)下游反滤排水体失效对总水头分布影响不大，但坝基砂层渗透比降增大，说明此时部分渗流绕经坝基排出，下游坝壳及坝基材料良好的排水性有效防止了浸润线抬升。

(4)随着上下游水位差增大，渗漏量也逐步增大；截渗墙失效后，总水头线向两侧扩散，导致两侧地基中渗透比降增大；黏土心墙及截渗墙失效后单宽渗漏量增加明显，说明两个部位是控制渗漏的关键部位，施工过程中重点加强质量控制，建成运行后进行重点监测。

(5)心墙土石坝断面设计合理，正常工况渗流水力要素计算结果符合要求，部分坝体区域失效对坝体整体的渗透安全影响不大，说明设计断面适应性好，安全保障程度高。

5 结语

基于ANSYS热分析模块二次开发得到的渗流程序，能够很好实现土石坝渗流场数值模拟，可广泛应用于土石坝断面设计、优化及相关研究；对老岚水库土石坝渗流特性的研究成果，为工程建设期质量控制及建成后渗流安全监测提供指导。但由于地质条件的复杂性，所建立土石坝渗流模型及相关参数特别是非饱和土相对渗透系数确定是否合理，应在工程建成后与实际渗流观测资料对比、分析，根据实测资料完善模型、优化参数，还可进一步研究建立三维模型对老岚水库土石坝渗流特性做更进一步研究。