一种CPP- RPP- PRR 解耦并联机构的位置反解分析
2022-10-26战丽娜肖淑斌
战丽娜,赵 楠*,肖淑斌
(湖南水利水电职业技术学院,湖南 长沙 410131)
机构的位置分析指的是求解机构的输入与输出构件之间的位置关系的过程。当已知机构输入件的位置和姿态,求解机构输出件的位置和姿态时称为机构位置分析的正解;当已知机构输出件的位置和姿态,求解机构输入件的位置和姿态时称为机构位置分析的反解[1-7]。本研究运用螺旋理论[7],对CPP-RPP-PRR解耦并联机构的位置反解进行了分析。
1 CPP-RPP-PRR 解耦并联机构结构概述
CPP-RPP-PRR 解耦并联机构主要由动平台、静平台和分别固连在两平台之间的三个分支组成。分支一包括一个圆柱副C1和两个移动方向相互垂直的移动副P1、P2,其中圆柱副C1在静平台上,其移动方向是静平台的竖直方向,且与移动副P1的移动方向相互垂直;分支二包括一个转动副R1和两个移动方向相互垂直的移动副P3、P4,其中转动副R1在静平台上,其回转轴线是静平台的竖直方向,且与移动副P3的移动方向相互垂直;分支三包括一个移动副P5和两个回转轴线相互平行的转动副R2、R3,其中移动副P5在静平台上,其移动方向是静平台的水平方向,且分别与转动副R2的回转轴线和转动副R3的回转轴线相互垂直。因此,从总体上看,圆柱副C1的回转轴线与转动副R1的回转轴线、转动副R2的回转轴线和转动副R3的回转轴线均两两相互平行,且都与移动副P5的移动方向相互垂直,其结构简图见图1。

图1 CPP-RPP-PRR 解耦并联机构结构简图
2 螺旋理论
对CPP-RPP-PRR 解耦并联机构进行位置反解分析,须以螺旋理论为基础。螺旋又称旋量,线矢量是旋量的特殊形式,可以表示空间矢量的方向和位置,每个螺旋都含有6 个标量。若把空间的两点A 和B 用有向直线连接,就能决定这条空间直线AB 的方向和位置。在直角坐标系中这条有向直线AB 的矢量可用S 表示,则直线AB 的方向可由其方向余弦确定,直线AB 的位置可通过直线上任意一点的矢量确定。因此,用螺旋来表示直线AB 就为=(S;S0),其中,S0=r×S,S·S0=0。若S·S0≠0,则表示的就为旋量[7]。
在并联机构中,刚体的转动副可以用刚体的角速度的大小与一个表示旋转轴作用线的单位线矢之积来表示,由于线矢之积与标量表示同一线矢,故转动副可用螺旋表示为:

刚体的移动副也可看成是一个瞬时转动,转动轴线与S 正交,且位于距S 无穷远的平面内,则移动副可用螺旋表示为:

其中,0 是一个1×3 的零矢量。
而圆柱副(C)则可看作共轴的一个转动副和一个移动副的组合。
3 CPP-RPP-PRR 解耦并联机构位置反解分析
CPP-RPP-PRR 解耦并联机构求解位置反解,即当给定机构的尺寸参数,已知动平台的未知参数(x,y,)及姿态角c,求三个驱动的输入:分支一的转动角度a、分支二的移动e、分支三的转动角度b。
由于该机构只能完成动平台在XY 平面的移动和绕Z 轴的转动,所以只需考虑XY 平面的运动即可求解位置反解。
在XY 平面内,如图2 机构平面简图所示,设静平台的杆长分别为L、g,分支一的杆长分别为l、d,分支二的杆长分别为e、f,分支三的杆长为H,动平台正多边形的内切圆半径为R,分支一与静平台之间的夹角为u,分支一与分支二之间的夹角为v,分支三与静平台之间的夹角为w,分支二与动平台之间的夹角为z,则L、H、R 三个杆长为定值,u、v、w、z 四个夹角也为定值,都不会随着机构的运动而改变,但是d、f、g、l 的长度会随着输入的改变而变化。设基坐标建立在分支三的圆柱面圆心A 点,动坐标建立在动平台中心,其余各个坐标建立见图3。

图2 CPP-RPP-PRR 解耦并联机构平面简图
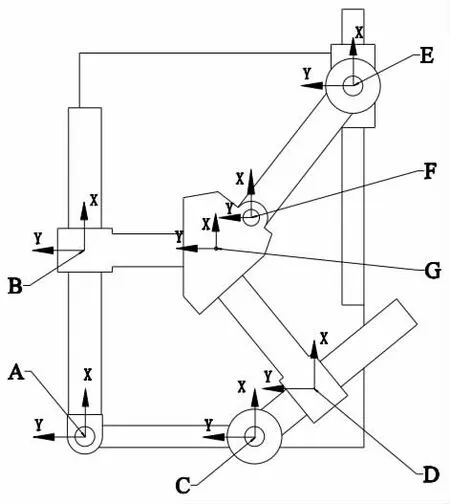
图3 CPP-RPP-PRR 解耦并联机构坐标系示意图
由图3 可知,动坐标位姿可以通过三条路线给定,路线一为A-B-G;路线二为A-C-D-G;路线三为A-E-F-G[6]。
根据螺旋理论,对路线一进行计算,得矩阵如下


对T1进行化简,得

根据螺旋理论,对路线二进行计算,得矩阵如下

对T2进行化简,得
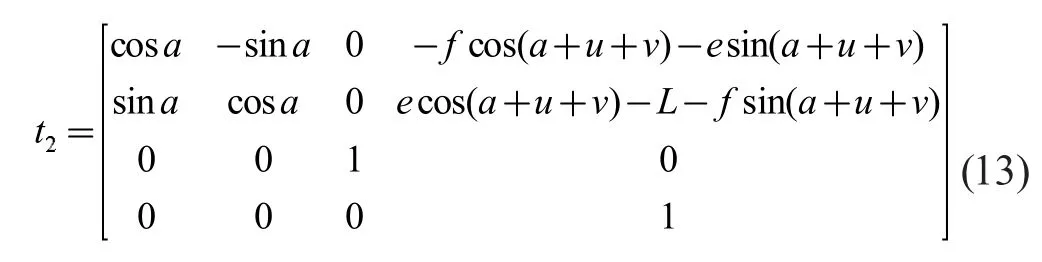
根据螺旋理论,对路线三进行计算,得矩阵如下


对T3进行化简,得

由结果可知,分支一的输入角度a 就是动平台的转动角度c 的值。再将式(7)、(13)、(20)三个矩阵的第四列分别相等,可列出六个方程如下

解出各分支的杆长l、d、e、f、g 和分支三的输入角度b 如下


4 验证CPP-RPP-PRR 解耦并联机构位置反解的正确性
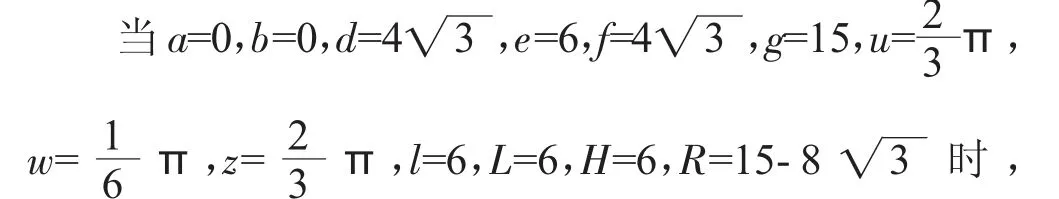
CPP-RPP-PRR 解耦并联机构处于特殊位置,将其分别代入式(3)、(4)、(5)、(6)、(8)、(9)、(10)、(11)、(12)、(14)、(15)、(16)、(17)、(18)和(19)中,得

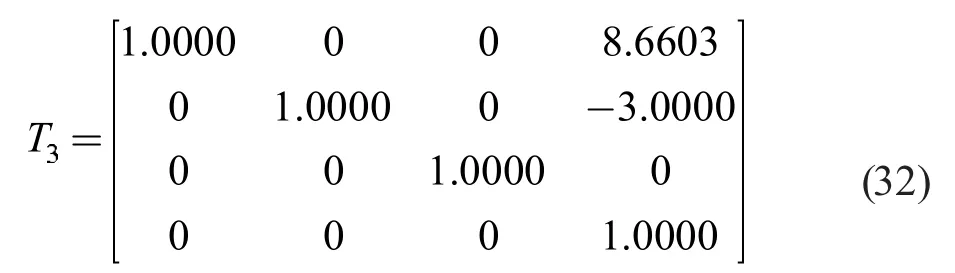
因此,机构的位置反解正确,即式 (29)为CPP-RPP-PRR 解耦并联机构的位置反解。
将该机构在ADAMS 软件中进行仿真分析验证,验证了该机构确实具有三个自由度,并得处分支三的运动轨迹曲线和计算一直,自由度验证结果见图4,分支三的运动轨迹曲线见图5。
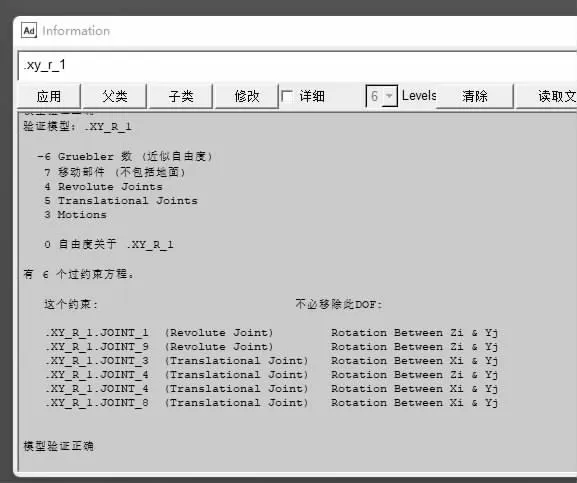
图4 自由度验证结果

图5 分支三运动轨迹曲线
5 结论
(1)分析CPP-RPP-PRR 解耦并联机构的结构,应用螺旋理论,给出该机构位置反解的整个推导过程。
(2)得出CPP-RPP-PRR 解耦并联机构的位置反解求解公式,并进行特殊位置验证,为该机构进一步的速度分析、加速度分析、受力分析、误差分析、工作空间分析、动力学分析和机构综合等奠定了理论基础。
