A Survey of Output Feedback Robust MPC for Linear Parameter Varying Systems

Xubin Ping, Jianchen Hu, Tingyu Lin, Baocang Ding, Peng Wang, and Zhiwu Li,

Abstract—For constrained linear parameter varying (LPV)systems, this survey comprehensively reviews the literatures on output feedback robust model predictive control (OFRMPC) over the past two decades from the aspects on motivations, main contributions, and the related techniques. According to the types of state observer systems and scheduling parameters of LPV systems, different kinds of OFRMPC approaches are summarized and compared. The extensions of OFRMPC for LPV systems to other related uncertain systems are also investigated. The methods of dealing with system uncertainties and constraints in different kinds of OFRMPC optimizations are given. Key issues on OFRMPC optimizations for LPV systems are discussed. Furthermore, the future research directions on OFRMPC for LPV systems are suggested.

I. INTRODUCTION

A. General Outline

MODEL predictive control (MPC) explicitly utilizes system models to predict system future behaviors and optimize the cost functions subject to physical constraints.Because of its ability to effectively handle systems with physical constraints in receding horizon optimal control optimizations, MPC has been extensively studied in both academia[1]–[7] and engineering industries [8]–[12]. In real processes,there often exist system uncertainties (e.g., parametric uncertainties, disturbances and/or noises). It is well known that robust MPC (RMPC) optimizations can guarantee system robust stability and constraint satisfaction by explicitly incorporating both system uncertainties and physical constraints[13]–[15].

With related to scheduling parameter and the constrained convex set composed of linear sub-models, linear parameter varying (LPV) systems can effectively approximate nonlinear systems or represent uncertain systems in linear system framework [16]–[19]. For quasi-LPV systems, the scheduling parameters of LPV systems are available at the current time but unknown in future, i.e., the LPV system parameters are known at the current time but uncertain within a bounded convex set in future. When the scheduling parameters of LPV systems are unknown at each sampling time, both the current and future system parameters are uncertain within a bounded convex set. For LPV systems, the properties of linear dynamics are dependent on the scheduling parameters, and system nonlinearities and uncertainties can be embedded in the solution set of a linear dynamic input-output relationship which varies with the scheduling parameters. Moreover, it is a common sense that a system model is always subject to unknown dynamics and/or small persistent disturbances, and the sensors in a system inevitably incorporate measurement noises in real processes. By employing the well-developed theories and techniques for linear systems, RMPC approaches proposed for uncertain or nonlinear systems represented by LPV models with bounded disturbances and/or noises can efficiently optimize controllers in receding horizon optimizations, hence have attracted more and more attention [20], [21].

A common property of most RMPC approaches developed for LPV systems in the state-space model framework relies on available system states. From a practical point of view, the assumption that system states are available during control implementation is often impractical, and only system outputs with noises or partial system states are available. Therefore,output feedback RMPC (OFRMPC) is more significant than state feedback RMPC for practical processes. There are three main reasons to investigate OFRMPC approaches for LPV systems: 1) For the systems with measurable states, state feedback RMPC schemes for LPV systems are becoming mature;2) RMPC can be well accepted for wide practical applications only if OFRMPC is well-studied; 3) To further develop adaptive RMPC with on-line system identifications, we have to know the properties of OFRMPC.

Compared with state feedback RMPC, the synthesis of robust state estimation and control in OFRMPC is more complex. Due to the coupling between observer and controller parameters in output feedback control optimizations, there are often no effective separation principles to ensure closed-loop stability [22], [23]. Then, the existences of both estimation errors and system uncertainties complicate the robust stability conditions and physical constraints in receding horizon solved OFRMPC optimizations. Hence, the state estimation errors in OFRMPC optimizations bring new problems for guaranteeing recursive feasibility and robust stability [2]. Nevertheless, the majority of available OFRMPC works have to consider the inclusion of estimation error bounds in RMPC optimizations when state observer systems are used.

B. Overview of RMPC for LPV Systems

We often refer to an RMPC scheme with guaranteed recursive feasibility and stability as RMPC synthesis approach [3].In this section, the RMPC controller synthesis theories and techniques for LPV systems reviewed in this survey are briefly introduced. It is well known that the main difficulty in RMPC for LPV systems is that the future predicted system states are dependent not only on future control inputs, but also on future unknown scheduling parameters. In the last three decades, by employing invariant set theories [24], [25], the techniques of robust optimization, linear matrix inequality(LMI) [26], and tube-based methods [27], RMPC synthesis approaches for uncertain systems have attracted much attention [1]–[6], [13], [16]. With the foundations of invariant set theories, the authors in [3] consider terminal set, terminal cost,and constrained system performance to formulate MPC optimizations with guaranteed recursive feasibility and stability.The developed procedures in [3] are important for optimal control of uncertain systems with physical constraints, since they allow the controlled systems to be steered towards the target reference by optimizing control performance with considering of physical constraints, recursive feasibility and robust stability.

According to the above theories and techniques, several strategies have been developed for RMPC controller design to counteract the effects of system uncertainties. Examples include the min-max optimization that incorporates the current and future system uncertainties in the worst cases into RMPC control formulations, and the tube-based RMPC approach that stabilizes nominal systems with tightened constraints [14]. The min-max optimization minimizes the upper bound of an infinite-horizon cost function with worst-case scenarios, i.e., all the possible realizations of current and future closed-loop system uncertainties are considered in RMPC optimizations. In min-max RMPC optimizations for LPV systems, the current and future closed-loop system states are often bounded within one common robust positively invariant (RPI) set, where all the possible realizations of system uncertainties are handled by resorting to the technique of LMIs. As an extension of min-max RMPC optimization,quasi-min-max RMPC optimizations exploit available system model information to reduce conservativeness. Compared with min-max RMPC optimizations, quasi-min-max RMPC optimizations minimize the upper bound of an infinite-horizon cost function by considering quasi-worst-case scenarios,where the first stage cost function in “max” operation is not involved.

Tube-based RMPC is an effective approach which is initially introduced for robust control of linear systems subject to bounded disturbances [28]. In tube-based RMPC optimizations, the controlled systems are stabilized by considering nominal system predictions with tightened constraints, in which system uncertainties are bounded within robust tubes.The techniques of tube-based RMPC for linear systems have been extended to LPV systems in recent years, which can deal with RMPC optimizations with both parametric uncertainties and/or bounded disturbances. The notion of tube-based RMPC for LPV systems is different from that for linear systems with bounded disturbances. In the tube-based RMPC approaches for LPV systems, the uncertainties due to unknown future scheduling parameters should be further dealt with in robust tubes and tightened constraints.

In state feedback RMPC approaches for LPV systems, the authors in [29] optimize the state feedback controllers by minimizing an infinite-horizon objective function respecting input and state constraints. By employing the invariant set theory[24], [25] to deal with predicted closed-loop system states, the constraints of the min-max optimization in [29] are formulated as LMIs and solved via semi-definite programming(SDP). Since the milestone contribution in [29], many state feedback RMPC approaches for LPV systems formulated as SDP optimizations have been developed [2], [4], [30]. The studies on state feedback RMPC approaches mainly focus on reducing the conservativeness in control optimizations to improve control performance, and reducing the on-line computational burden of real-time RMPC algorithms. In [31], a state feedback RMPC approach for LPV systems with bounded rates of parameter changes is designed to reduce the conservativeness of feedback controller. The parameterdependent control laws in [32] reduce the conservativeness in RMPC optimization and obtain better control performance. To reduce the conservativeness in state feedback RMPC optimizations, the quasi-min-max optimizations with one free control move are studied in [33]–[36], where bounded rates of parameter changes are considered in [34] and [35]. The online min-max RMPC optimizations often suffer from expensive computational burdens [37]. In [38]–[41], the off-line state feedback RMPC approaches based on a look-up table strategy are employed to reduce on-line computational burdens. For the tube-based state feedback RMPC methods in[42]–[44], the future system uncertainties resulting from uncertain and bounded variations of scheduling parameters are incorporated within robust tubes. Then, RMPC optimizations are formulated as quadratic programming subject to tightened constraints, and solved to steer the nominal system towards the origin to guarantee robust stability of the controlled LPV systems.

In OFRMPC approaches for LPV systems, the relationships between robust state estimation and control should be simultaneously considered. An important issue in OFRMPC optimizations is how to choose a state observer system in the presence of system uncertainties and physical constraints. It is well known that the joint design of state observer and feedback controller in the presence of physical constraints is often difficult [15]. Compared with state feedback RMPC optimizations, estimation error bounds should be further included in robust stability conditions and physical constraints. Most of the existing studies on min-max OFRMPC approaches for LPV systems are characterized by stabilizing closed-loop systems via synthesizing the parameters of observer and controller. However, simultaneously optimizing the parameters of observer and controller in observer-based OFRMPC optimizations, and controller parameters in dynamic OFRMPC optimizations often results in a non-convex bilinear matrix inequality (BMI) problem and cannot be solved in polynomial time [45], [46], which motives many researchers to develop different techniques to reformulate non-convex OFRMPC optimizations as efficient convex one. OFRMPC approaches for uncertain systems with physical constraints have been extensively studied over the past two decades.When both system parametric uncertainties and bounded disturbances and/or noises are considered, the main difficulties for OFRMPC optimizations arise because it is hard to predict the future system evolutions due to future parametric uncertainties and unknown system states, which have attracted a lot of attention to the development of OFRMPC optimizations for LPV systems with bounded disturbances and/or noises.

In general, the presence of system uncertainties, estimation error sets, bounded disturbances and/or noises brings important consequences for the theory of OFRMPC optimizations because it affects the issues of both robust stability and constraint satisfaction. Both the min-max and tube-based RMPC optimizations are applicable for OFRMPC formulations,where the influences of time-varying estimation error bounds should be further considered in robust stability and constraint conditions. To formulate min-max OFRMPC optimizations for LPV systems, different types of state observer systems can be designed to estimate unknown system states, and based on which the corresponding closed-loop systems can be constructed. Then, by employing the invariant set theory, the techniques of LMIs and convex optimizations, OFRMPC optimizations subject to robust stability and physical constraints can be formulated. When OFRMPC optimizations are solved in receding horizon fashion, real-time estimation error (or system state) bounds should be updated and considered in robust stability and physical admissibility. To obtain estimation error(or system state) sets, the technique of set-membership estimation [47] is often employed to perform set operations,where nonstatistical uncertainties (such as model parameters,estimation error sets, bounded disturbances and/or noises) are described in the form of bounded uncertainties. Other than the tube-based OFRMPC approaches developed for linear systems with bounded disturbances and noises (e.g., [48]–[51]),tube-based OFRMPC approaches have been proposed for LPV systems with bounded disturbances and noises (e.g.,[52]–[54]).

C. Motivation, Contribution and Organization

There have been plenty of results on OFRMPC approaches developed for LPV systems over the past two decades. Nevertheless, the motivations, main contributions, and the relationships between different OFRMPC formulations have not been fully and clearly discussed and compared. This survey comprehensively summarizes and analyzes the studies on OFRMPC for LPV systems over the past two decades, and attempts to suggest the research directions for its future developments. In this survey, different kinds of OFRMPC approaches are classified according to the types of state observer systems and scheduling parameters of LPV systems.ORFMPC approaches for other uncertain systems related to LPV systems are introduced. Furthermore, the relationships among different kinds of OFRMPC approaches are compared.For the investigated different kinds of OFRMPC works, the methods of dealing with system uncertainties and constraints on bounded disturbances and/or noises, the current system state, robust stability, control inputs, system states and outputs are given. Then, key issues on OFRMPC for LPV systems (such as non-convex BMIs, estimation error constraints and bounds, recursive feasibility and robust stability, control performances and computational burdens) are discussed. By comparing and analyzing the reviewed literatures on OFRMPC for LPV systems, the main motivations, contributions, and techniques for different OFRMPC approaches are summarized and explained. Furthermore, the future research directions on OFRMPC for LPV systems are suggested.

The rest of the survey is organized as follows. Section I-D lists basic notations. Section I-E describes a constrained LPV system with bounded disturbances and noises. In Section II,different kinds of OFRMPC approaches are classified. In Section III, ORFMPC for LPV systems is extended to other related uncertain systems. In Section IV, the relationships between different OFRMPC approaches are discussed. In Section V, the methods that can deal with system uncertainties and unknown system states for different OFRMPC optimizations are shown. In Section VI, robust stability conditions are formulated. In Section VII, the methods that can deal with physical constraints on control inputs, system states and outputs are given. In Section VIII, a number of key issues on OFRMPC optimizations for LPV systems are discussed. In Section IX, the future research directions on OFRMPC approaches for LPV systems are suggested. Finally, conclusions are drawn in Section X.

D. Basic Notations

E. System Description

A discrete-time constrained LPV system with bounded disturbances and noises is considered

II. CLASSIFICATION OF OFRMPC APPROACHES

Classifying the available literatures on OFRMPC for constrained LPV systems is quite difficult due to the large variety of OFRMPC formulations and solutions. However, most of OFRMPC approaches share some common basic methodologies, and it is of great importance to summarize their main common features and differences. In [55], some works on dynamic OFRMPC approaches are introduced. In this section,different OFRMPC approaches are comprehensively summarized according to the types of state observer systems and scheduling parameters of LPV systems.

A. Dynamic OFRMPC for Quasi-LPV Systems

In [56]–[64], the dynamic output feedback controllers are dependent on weighting functions, and closed-loop robust stability is guaranteed by the technique of quadratic boundedness [65], [66]. The OFRMPC optimizations in [56]–[62]include main optimizations to optimize dynamic output feedback controller parameters, and separated auxiliary optimizations to update estimation error bounds. The main optimization is the min-max one to ensure that the current and future closed-loop system states are bounded in one common RPI set. By taking the parameter-dependent controller parameters in (8) and employing the techniques of LMIs, the main optimizations in [56]–[64] are solved as SDP optimizations such that the dynamic output feedback controller parameters in (6)and (7) can be obtained (see the details in [58], [59], [61]).However, parameter-dependent dynamic controller parameters often introduce more decision variables and LMI constraints in OFRMPC optimizations, which increase on-line computational burdens and hinder their applications to high order systems.

The dynamic OFRMPC optimizations in [56]–[60] consider polyhedral estimation error sets, where auxiliary optimizations not only update estimation error bounds, but also determine whether the main optimizations at the next sampling time are feasible. The precise polyhedral estimation error bounds in [56]–[60] not only reduce the conservativeness of optimized dynamic output feedback controller parameters, but also are advantageous for the feasibility of the main optimizations at the next sampling time. In [56], the estimation error constraints are involved in the main optimization and updated once the main optimization is solved. In [57] and [58], the auxiliary optimizations are iteratively solved to optimize timevarying transformation matrices such that the polyhedral estimation error bounds with fixed vertices can be updated. In[57], the method of updating estimation error bounds is related to that in [56], where two transformation matrices related to system states and controller states are optimized in auxiliary optimizations. Differently from [57], the estimation error bounds in [58] are obtained by computing vertices of polyhedral sets via the estimation error system. Then, the transformation matrix related to the estimation error set is optimized. In[59], a non-iterative auxiliary optimization optimizes the matrices related to the true state bounds at the next sampling time. Compared with [57] and [58], the computational burden of the OFRMPC optimization in [59] is reduced and the control performance is improved.

For the dynamic OFRMPC approach in [60], the polyhedral estimation error sets are represented as zonotopes [67] and updated via the zonotopic set-membership state estimation. By properly selecting the orders of zonotopes, precise polyhedral estimation error bounds can be computed, and the control performance of the OFRMPC optimization in [60] is improved.The off-line dynamic OFRMPC approaches in [63] and [64]reduce the on-line computational burden. In [63], the fixed polyhedral estimation error constraints are included in off-line OFRMPC optimizations, but estimation error constraints in[64] are removed from off-line OFRMPC optimizations. The real-time searched controller parameters in [63] satisfy estimation error constraints. The relaxation methods in [68] are employed in [64] to reduce the conservativeness in dealing with the constraints on control inputs and system states. In[64], both time-varying polyhedral and ellipsoidal sets are computed and compared to update estimation error bounds.

In [61], according to the estimation error system and the invariance condition of the closed-loop system, a polyhedral estimation error set and an ellipsoidal estimation error set are respectively computed and compared to ensure recursive feasibility of the dynamic OFRMPC with polyhedral estimation error sets. In [61], the calculation of polyhedral estimation error bounds based on the estimation error system is complex,since the polyhedral outer approximation of ellipsoids and the outer approximations of polyhedral set via ellipsoids are involved. For the dynamic OFRMPC approach in [62], the ellipsoidal estimation error set based on an estimation error system is directly computed by applying the S-procedure [69].In [62], two ellipsoidal estimation error sets are computed via respectively the invariance of the closed-loop system and the estimation error system, and then compared to guarantee recursive feasibility of the OFRMPC optimization.

The dynamic OFRMPC approach with a larger number of periodic invariant sets in [70] enlarges the feasible region and improves the control performance at the cost of heavier computational burden. In [71], the synchronization for chaotic systems with unknown system states is formulated as a dynamic OFRMPC optimization with mixedH2/H∞cost function.

B. Dynamic OFRMPC for LPV Systems

When the scheduling parameters of the LPV system (1) and(2) are unknown at each sampling time, the dynamic output feedback controller is

The technique of quadratic boundedness in [65] and [66]can also be employed to achieve robust stability conditions for system (12). Compared with the dynamic OFRMPC approaches for quasi-LPV systems in Section II-A, the LPV system scheduling parameters are unknown at each sampling time such that the controller parameters in (10) and (11) cannot take the parameter-dependent form as in (8). On-line simultaneously optimizing the dynamic output feedback controller parameters in (10) and (11) often results in non-convex BMIs due to the existence of inverse matrix variables in OFRMPC optimizations (see the following condition (53)).

The dynamic OFRMPC approaches with ellipsoidal estimation error sets in [72]–[89] and with polyhedral estimation error sets in [90]–[95] are investigated. The dynamic OFRMPC for approaches LPV systems often include main optimizations to obtain dynamic output feedback controller parameters, and auxiliary optimizations to update estimation error bounds. To deal with the difficulties of solving non-convex BMIs in dynamic OFRMPC optimizations, the performance indices of the min-max optimizations and dynamic controller parameters can be iteratively optimized as in [72],[73], [79], [91], and [94] by employing the cone complementarity linearization approach in [97]. The computational burdens of OFRMPC optimizations via cone complementarity linearization approach are often costly due to iteratively solving OFRMPC optimizations. To deal with the difficulties resulting from solving non-convex BMIs, the following two strategies are often selected.

1) Reformulation of Non-Convex BMIs as Convex LMIs:In[74]–[77], [79], [81]–[83], and [95], partial parameters{Lc(k),Fy(k)} are off-line optimized at the initial timek=0 and fixed in on-line dynamic OFRMPC optimizations. Then,the other parameters {Ac(k),Fx(k)} can be on-line optimized via convex SDP optimizations subject to LMI constraints. The dynamic OFRMPC approach in [79] fuses the merits of [72],[76], and [96], where the introduced variant cone complementarity linearization approach can guarantee recursive feasibility and reduce the computational burden. For LPV systems without bounded disturbances and noises, the dynamic OFRMPC approaches in [86] and [87] take the similar dynamic output feedback controllers as in [98], where two independent auxiliary controller gains related to the feedbacks on the controller state are additionally introduced. In[86] and [87], the dynamic controller parameters can be offline designed via the method in [58]. Then, two independent auxiliary controller gains can be on-line optimized via SDP optimizations.

In [84], [99], and [100], by making proper assumptions on system structure (i.e., the system matrices related to measurements are assumed to be full row rank) and applying the techniques of matrix inequalities, convex dynamic OFRMPC optimizations for LPV systems without bounded disturbances and noises are formulated. For LPV systems with bounded disturbances, by employing the Young’s inequality in [101],dynamic output feedback controller parameters with the corresponding performance index are simultaneously on-line obtained in [85] via an SDP optimization. In [102], a convex dynamic OFRMPC optimization with bounded disturbances and noises improves the algorithm proposed in [84] and does not require any special structure of LPV system matrices.

2) Design of Off-Line Dynamic OFRMPC Approaches:The off-line dynamic OFRMPC approaches often include constructing a look-up table to off-line store optimized dynamic output feedback controller parameters with the corresponding regions of attraction, and on-line searching dynamic controller parameters based on real-time controller states and estimation error bounds. The off-line dynamic OFRMPC approaches with polyhedral estimation error sets in [92] and [93],and with ellipsoidal estimation error sets in [80] and [86]–[89]are respectively studied. Compared with [92], the algorithm complexity of searching real-time controller parameters in[93] is simple with lower computational burden. In [86] and[89], both the constraints on the estimation error and controller state are involved in off-line OFRMPC optimizations.However, only controller state constraints in [87] and estimation error constraints in [88] are required to be considered.

The off-line optimized feasible regions for controller states in [86]–[89] are often small invariant sets. For the off-line dynamic OFRMPC with time-varying ellipsoidal estimation error sets in [80], the estimation error constraints are not considered in off-line OFRMPC optimizations and the feasible region of controller states is enlarged. For the off-line dynamic OFRMPC approach in [103], both ellipsoidal and polyhedral state bounds are computed and compared to update estimation error bounds. In [72], [73], [77], [78], [82], and[83], ellipsoidal estimation error bounds are refreshed via the invariance of closed-loop systems to ensure recursive feasibility of OFRMPC optimizations. In [74]–[79] and [85], the estimation error sets calculated respectively from closed-loop systems and estimation error systems are compared to ensure recursive feasibility and reduce the conservativeness of updating estimation error bounds. The work in [83] includes the contributions in [63], [72], and [96] as special cases, and can improve the control performance and enlarge the region of attraction.

For the dynamic OFRMPC approach with polyhedral estimation error sets in [90], transformation matrices are optimized to update polyhedral estimation error bounds. The author in [91] improves the approach in [90] by obtaining a near-optimal solution to OFRMPC problem and directly updating system state bounds. For the off-line dynamic OFRMPC approaches in [92] and [93], polyhedral estimation error sets are updated via computing polyhedral vertices and then outer approximated via pre-specified boxes. The dynamic OFRMPC approach in [94] further combines the merits of updating polyhedral estimation error bounds in [90] and [91].To simplify the procedure of updating polyhedral estimation error bounds in dynamic OFRMPC, the uncertain system parameters in [95] are described as interval matrices. Then,polyhedral estimation error sets are computed by applying the properties of interval matrices and zonotopic set-membership state estimations. In [90], [91], [94], and [95], recursive feasibility of dynamic OFRMPC optimizations is not guaranteed,where the auxiliary optimizations not only update estimation error bounds, but also determine whether the main optimizations at the next sampling time are feasible. In [81], a systematic treatment of system true state bounds is discussed, which combines the merits of polyhedral estimation error bounds in[61] and [94], and ellipsoidal estimation error sets in [76].

To reduce the conservativeness of control inputs, dynamic OFRMPC approaches with saturated control inputs are designed in [87], [99], and [100]. In [87], partial dynamic output feedback controller parameters should be pre-specified in advance. In [99], all dynamic output feedback controller parameters are simultaneously optimized, which is the extension of the OFRMPC approach in [87]. Furthermore, an additional condition is used in [99] to guarantee recursive feasibility. The work in [100] further improves the method in [99] by proposing an OFRMPC approach with full on-line synthesis of dynamic output feedback controller parameters through a convex optimization. A dynamic OFRMPC approach with saturated control inputs is studied in [75] for LPV systems with bounded disturbances. Since the invariant conditions on controller states are considered in [75] and [87], the RPI sets for controller states and estimation errors are optimized at each sampling time. Furthermore, the estimation error bounds at the next sampling time are optimized in [87], and the estimation error bounds in [75] are updated by comparing two ellipsoidal sets computed respectively from the estimation error system and the invariance of closed-loop system.

Although the control performances of OFRMPC approaches in [87], [99], and [100] can be improved via saturated control inputs, the on-line computational burdens are increased because of the additionally introduced auxiliary feedback controller decision variables and LMI constraints (see the details in Section VIII-D). In [104], to reduce the conservativeness of control inputs, one free controller state and one free control move are introduced in the dynamic output feedback controller and directly optimized in OFRMPC optimizations. The work in [76] combines the merits of the works in [63], [72],and [96], and improves the dynamic OFRMPC approach via the utilization of full Lyapunov matrix, treatment of physical constraints with norm-bounding technique, and multi-step closed-loop predictions.

C. Observer-Based OFRMPC for Quasi-LPV Systems

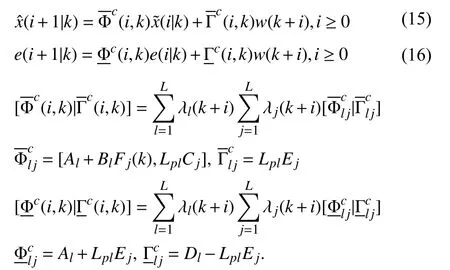
In the observer-based OFRMPC approaches for quasi-LPV systems, the following state observer system is often considered (e.g., [105] and [106]):parameters in (2) are assumed to be constant matrices (i.e.,C(θk)=CandE(θk)=E). In [105]–[118], the estimation error systems are autonomous one. In [105]–[108], by exploiting the technique of quadratic boundedness, the sufficient and necessary conditions on RPI sets for estimation error systems with the corresponding minimal RPI sets are developed to offline optimize state observer gains. By employing the techniques of the S-procedure and RPI sets, the sufficient robust stability conditions for estimation error systems are formulated in [115]–[118]. The robust stability of the estimation error systems in [105]–[109], [115], and [118] is ensured by the off-line optimized state observer gains.

For the OFRMPC approaches in [105]–[108], [118], the real-time estimation error bounds are obtained by scaling the minimal RPI sets for estimation error systems via on-line optimized scalars. The update of estimation error bounds in [109]is complex, as a comparison of different optimized positive scalars is required. Differently from the cost functions in common min-max MPC optimizations, anH∞-type cost function of MPC optimization is considered in [106], and a mixedH2/H∞cost function is investigated in [108]. Compared with the common cost function in min-max OFRMPC optimizations, theH∞-type cost function in [106] is discussed in Sec-

The state observer and controller gains in (13) take the parameter-dependent form. The state observer systems in[107]–[114] are of the similar form as in (13), but their state observer gains are constant matrices. The state observer systems in [105]–[114] are prior Luenberger state observer systems. In [115]–[117], posterior Luenberger state observer systems are adopted. To deal with the robust stability constraints in [115]–[117] with fewer LMIs, the system measurement tion VI-C. OFRMPC optimizations for LPV system with different cost functions can achieve different robust stability conditions, where the main objective is to ensure that the controlled closed-loop systems are bounded and convergent in RPI sets with satisfying optimality conditions.

Differently from the dynamic OFRMPC approaches in[58]–[61], the polyhedral estimation error sets in [116] are represented as zonotopes and updated via zonotopic set-membership state estimation, which simplifies OFRMPC optimizations with polyhedral estimation error bounds. Furthermore,the quasi-min-max optimization in [116] reduces the conservativeness of control inputs. The time-varying orders of zonotopes and their order reductions have to be considered in[116]. In [118], the upper and lower bounds of estimation error sets with the fixed number of polyhedral vertices are calculated via zonotope-based box computations. The OFRMPC approach with ellipsoidal set-membership state estimation is designed in [110], where robust stability is achieved by adding a terminal state constraint in MPC optimization. In [111],polyhedral estimation error sets decrease as the pre-specified rate and the stabilization problem considers the outer approximations of polyhedral estimation error sets via ellipsoids. The min-max OFRMPC optimizations in [105] and [108], and quasi-min-max optimizations in [109] and [111] are solved to optimize on-line controller gains to achieve robust stability of closed-loop systems. The quasi-min-max OFRMPC optimizations in [107], [116], and [118] are solved to ensure robust stability of closed-loop observer systems.

Off-line optimized state observer gains often introduce conservativeness in on-line observer-based OFRMPC optimizations. In [112], by assuming that the system parameters have special structure (see Remarks 1 and 2 in [112]), the state observer gain and controller gain can be simultaneously onlined optimized. It is shown in [112] that, other than the observer-based OFRMPC with off-line state observer gain, the observer-based OFRMPC approach with on-line state observer gain has a larger feasible region and better control performance. In [116], by employing the technique of the Young’s inequality, the state observer gain, feedback controller gain,and the estimation error set at the next sampling time are incorporated into one on-line quasi-min-max OFRMPC optimization. Since both the current and future controller and observer gains in a parameter-dependent form are optimized,the computational burden in [116] increases.

To reduce the computational burdens of observer-based OFRMPC optimizations, off-line look-up tables are constructed in [105] and [117] to store the off-line computed subobserver gains, sub-controller gains, and regions of attraction.In the on-line stage, according to real-time estimated states and estimation error bounds, the sub-observer gains are fixed and real-time sub-controller gains are searched in [105]; both time-varying sub-observer and sub-controller gains are searched in [117]. Compared with the off-line OFRMPC approach in [105], the feasible region for estimated states is enlarged in [117] by reducing the conservativeness in dealing with state constraints. Furthermore, the robust control invariant sets for estimated states and RPI sets for estimation errors in [117] are nested in theory for advantageously searching sub-observer and sub-controller gains.

To reduce the conservativeness of control inputs, an OFRMPC approach with one free control input is designed in[113]. However, as pointed out in [119], the simple combination of a stable observer gain and a feedback controller gain might not guarantee the closed-loop stability since the separation principle does not hold. The authors in [114] improve the work in [113] by designing a two-stage control mechanism,where system states are first steered into a prescribed region in the neighborhood of the origin, and then a terminal controller ensures that system states can converge to the origin. One free control input is also optimized in [109] and [111] to stabilize closed-loop systems. Compared with [111], bounded disturbances and time-varying ellipsoidal estimation error sets are handled in [109].

In [107], an observer-based OFRMPC algorithm with multistep closed-loop predictions is designed to steer the closedloop observer system to a neighborhood of the origin. However, the on-line computational burden in [107] significantly increases as the closed-loop prediction horizons increase. The OFRMPC optimizations in [107], [109], [111], [114]–[116],and [118] are quasi-min-max one such that the conservativeness in OFRMPC optimizations can be reduced by further considering the exactly known system parameters at the current sampling time. Then, their optimized control inputs are less conservative and can reach the boundaries of control inputs to exploit their full capabilities. The quasi-min-max OFRMPC optimizations with free control inputs in [109],[111], and [114] are difficult to deal with state constraints.Nevertheless, the multiple feedback controller gains are optimized in [107], [115], [116], and [118], where the RPI sets for closed-loop systems are involved and system state constraints are easy to be handled.

D. Observer-Based OFRMPC for LPV Systems

In [96], [120], [121], the following state observer system is considered:

To stabilize system (19), an off-line OFRMPC method based on a look-up table is proposed in [96]. By taking the state observer system (17) and (18), the authors in [120] and[121] formulate OFRMPC optimizations to investigate the security control problem for LPV systems subject to bounded disturbances and deception attacks, where the estimation error sets in [121] are updated via the invariance of a closed-loop system. Compared with the observer-based OFRMPC for quasi-LPV systems in Section II-C, the augmented closedloop system (19) is not easy to divide into a closed-loop observer system and an estimation error system. Then, it is often complex to synthesize the off-line state observer gain and on-line feedback controller gain. In [96]–[121], the state observer gains are off-line pre-specified, but deciding how to properly choose the off-line observer gains is not clearly given.

In [122]–[126], the state observer system is

An event-triggered dynamic OFRMPC approach with a time-varying threshold under redundant channel communication protocol is proposed in [125], where the observer gainL0in (20) is replaced by a time-varying observer gainL(k).An appropriate triggering mechanism is necessary in the convergent process for the controlled LPV systems to accelerate the convergent speed. Thus, the dynamic OFRMPC with the time-varying threshold event-triggering mechanism in [125] is selected as a monotonically decreasing and bounded function,which can better reflect the dynamic evolution of the controlled plant to some extent. In [125], by employing the technique of RPI sets and cone complementarity linearization approach, the state observer gain and feedback controller gain can be simultaneously obtained. However, the computational burden increases due to the iterations of cone complementarity linearization approach. In [126], an OFRMPC approach with periodic invariance provides a larger feasible region. The OFRMPC approach in [126] includes two stages: in the offline optimizations, the periodic estimator gains and periodic feedback gains are determined to provide robust stability for closed-loop system; in the on-line stage, the on-line optimization searches feedback controller gains and state estimator gains to guarantee robust stability of the closed-loop system.For the non-fragile observer-based distributed OFRMPC approach in [127], the on-line optimizations for subsystems can be executed in parallel, which is efficient to save computational time and improve system robustness and fault tolerance.

E. Tube-Based OFRMPC for Quasi-LPV Systems

In tube-based OFRMPC, the following state observer system (22) and nominal LPV system (23) without disturbances and noises are:

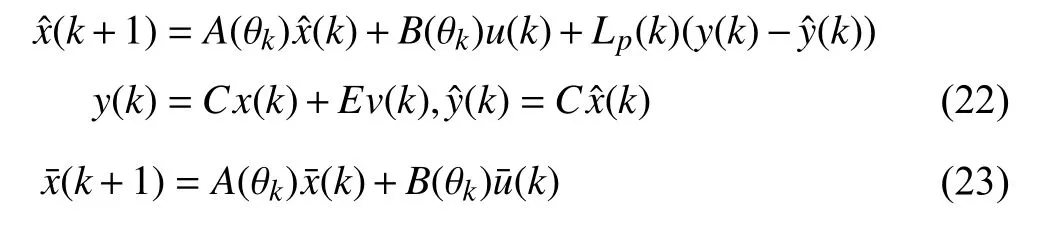
To simplify the tube-based OFRMPC approach, it is assumed that some system model parameters in (1) and (2) are constant with proper dimensions (i.e.,C(θk)=C,D(θk)=D,andE(θk)=E). For the tube-based OFRMPC approaches in[52] and [53], the estimation error and control error are bounded in minimal polyhedral RPI sets. Then, the quasi-minmax OFRMPC optimization in [52] and the min-max optimization in [53] are solved to stabilize the nominal system(23). The tube-based OFRMPC approaches in [52] and [53]include four parts: i) off-line optimize the state observer gain and ancillary feedback controller gain; ii) off-line compute the minimal RPI sets for the estimation error and control error; iii)obtain the tightened constraint sets for the nominal control input; iv) solve the quasi-min-max optimization in [52] or the min-max optimization in [53] to optimize the nominal control input and the nominal controller gain to stabilize the nominal system (23).

For the case that the initial estimation error set is larger than the minimal RPI set for estimation errors, the tube-based OFRMPC approaches in [52] and [53] are not applicable. The tube-based OFRMPC approach in [54] can be applicable for the above case by considering the tightened constraint sets for nominal states with different estimation error bounds. To this end, Algorithm 1 in [54] off-line synthesizes the above steps i)–iii) in [52] and [53], where the nested robust tubes respectively for estimation errors and control errors, with the corresponding state observer gains and the ancillary feedback controller gains, and the tightened constraints sets for nominal control inputs and nominal states are off-line optimized and stored in a look-up table. In [52] and [53], the robust tubes for estimation errors are related to system uncertainties, bounded disturbances and noises. However, different sizes of robust tubes in [54] are dependent on not only system uncertainties,bounded disturbances and noises, but also the sizes of estimation error bounds. In [54], according to real-time estimation error bounds, the constraint sets for estimation errors and control errors with the related state observer gains and ancillary feedback controller gains are searched. Then, the on-line quasi-min-max optimization considers a one-step ahead nominal state prediction and the scaled time-varying terminal constraint sets to stabilize the nominal system. Since model parametric uncertainties, different sizes of estimation error sets,bounded disturbances and noises are considered in the off-line computed robust tubes, the major drawback of the tube-based OFRMPC approach in [54] is the introduced conservativeness in control performance and feasible region.

F. OFRMPC for LPV Systems in Input-Output (IO) Models

In some cases, LPV systems can be modeled in IO form,and state observer systems are not required to estimate system states [128]. For LPV systems with bounded noises, the uncertain IO model can be represented as (e.g., [129]–[131])

The details on the matrices Φland Γlcan be found in [130].The min-max RMPC optimizations with control input and system output constraints are solved in [129]–[131] to stabilize the closed-loop system (29), where the quadratic boundedness is employed to guarantee robust stability. System (29) is constructed via the current and past system outputs and control inputs, where the dimensions of the augmented state increase as the orders of the IO model. Then, a larger number of LMI decision variables and constraints are introduced in on-line min-max RMPC optimizations with heavier computational burden. Furthermore, the Lyapunov matrices in[129]–[131] are diagonal form (i.e., some non-diagonal elements of Lyapunov matrices are zeros), which introduces conservativeness in RMPC optimizations.

G. Other Forms of OFRMPC Problems

There are some other forms of OFRMPC approaches. A robust static OFRMPC approach for LPV systems is studied in [132], where the control input is the feedback directly from system outputs and the technique of input saturation is employed to reduce the conservativeness. For LPV systems with linear fractional representation, a dynamic OFRMPC approach in [133] takes a parameter-dependent Lyapunov function and improves the control performance compared with the dynamic OFRMPC approach with a common Lyapunov function. For LPV systems with bounded disturbances and noises, a tube-based OFRMPC approach with multi-step openloop predictions solved as quadratic programming is proposed in [134]. The OFRMPC approach in [135] incorporates an interval observer into the set-membership estimation of system states. Then, an interval predictor is used in OFRMPC algorithm, which is an extension of the interval-observer based OFRMPC approaches for linear systems with bounded disturbances and noises in [136] and [137].

III. ExTENSIONS OF ORFMPC FOR LPV SySTEMS TO OTHER UNCERTAIN SySTEMS

The investigated OFRMPC approaches in Section II are mostly developed for uncertain systems represented in the LPV system framework. There are some other uncertain systems having close relationships with LPV systems. T-S fuzzy systems can be regarded as quasi-LPV systems if the membership functions for the former are treated as the weighting functions for the latter [138]. The traditional T-S fuzzy systems are known as Type-1 T-S fuzzy systems, where system nonlinearities in modeling are approximated via a set of linear submodes weighted by membership functions. Interval Type-2(IT2) T-S fuzzy systems are the collection of Type-1 T-S fuzzy models, which can describe nonlinear systems subject to parametric uncertainties [139]. Hence, IT2 T-S fuzzy systems are the extension of the quasi-LPV systems with parametric uncertainties in weighting functions. Furthermore, LPV systems modeled in the polytopic uncertain form can be approximated via linear systems with norm-bounded uncertainty [26],[140]. In this section, OFRMPC approaches for other related uncertain systems are introduced.

A. OFRMPC for T-S Fuzzy Systems

For T-S fuzzy systems with bounded disturbances, a dynamic OFRMPC approach with ellipsoidal estimation error sets is studied in [141]. To reduce the conservativeness of updating estimation error bounds, polyhedral estimation error sets in [141] based on estimation error system are computed,and then compared with ellipsoidal estimation error sets obtained from the invariance of closed-loop systems. The work in [68] improves the dynamic OFRMPC approach in[141] by utilizing a full Lyapunov matrix, introducing relaxation scalars for better handling the constraints on control inputs and states, and adopting multi-step dynamic output feedback controller gains. In [142], an observer-based OFRMPC approach for T-S fuzzy systems without disturbances and noises introduces one free control input, which is an extension of the state feedback RMPC with one free control input in [33]. The observer-based OFRMPC approach in [109]is an extension of the OFRMPC approach in [142] to quasi-LPV systems with bounded disturbances.

In [143], for T-S fuzzy network control systems, two observer-based OFRMPC approaches with and without one free control input are respectively studied. The observer-based OFRMPC with one free control input in [143] can be regarded as an extension of [109] and improves the control performance, compared with the observer-based OFRMPC without one free control input. In [144], for T-S fuzzy systems with disturbances, a dynamic OFRMPC approach parameterizes infinite-horizon control inputs and controller states, respectively, into one free control input and one free controller state followed by dynamic output feedback controller parameters.The additional one free control input and one free controller state in [144] introduce more freedoms for OFRMPC optimization, which results in better control performance than the dynamic OFRMPC approach in [141]. Compared with the observer-based OFRMPC approach with one free control input in [109], the dynamic OFRMPC approach with one free control move in [144] is complex and the optimized control inputs have conservativeness. In [145], a time-varying tubebased OFRMPC approach combines the look-up table in the off-line algorithm and the on-line quasi-min-max OFRMPC optimization to stabilize nominal system. In [145], the nested robust tubes for nominal states, estimation errors and control errors are optimized with the related nominal feedback controller gains, ancillary feedback controller gains and state observer gains, and then stored in a look-up table. According to real-time estimation error bounds, the on-line constraint sets for nominal states, control errors and estimation errors are searched in [145]. Then, the quasi-min-max MPC optimization with tightened constraints is on-line solved to stabilize the nominal system by optimizing nominal control inputs.

Motivated by the multi-step dynamic OFRMPC approaches in [76] and [144], the event-triggered multi-step OFRMPC for T-S fuzzy systems with structured uncertainties and bounded disturbances in [146] offers more freedoms in optimizations and obtains better control performance. In [146], infinite-horizon control moves are parameterized into a sequence of controller gains, where a larger closed-loop prediction step achieves better control performance at the cost of heavier computational burden. The authors in [147] propose an OFRMPC approach with steady-state target calculation to track time-varying targets calculated by the upper steady-state target calculation layer. Furthermore, a heuristic on-line OFRMPC approach withN(N≥1) free control moves is further introduced to reduce the conservativeness in control inputs.

B. OFRMPC for IT2 T-S Fuzzy Systems

For IT2 T-S fuzzy systems without disturbances and noises,a networked control with data quantization and packet loss is formulated in [148], and a networked control system under denial of service attacks and actuator saturation is studied in[149]. The observer-based min-max OFRMPC optimizations in [148] and [149] synthesize off-line state observer gains and on-line controller gains. The estimation error sets in [148] and[149] are updated by optimizing non-increasing positive scalars to scale an ellipsoid. The work in [150] introduces one free control input in the observer-based OFRMPC networked control system with packet loss, which can be taken as an extension of the work in [109]. An event-triggered min-max OFRMPC approach in [151] takes dynamic controller parameters in a parameter-dependent form to stabilize the networked control systems with packet loss. The quasi-min-max OFRMPC approach in [152] reduces the conservativeness of output feedback controllers by considering that the current and future estimated states (estimation errors) are bounded within different RPI sets. Furthermore, an off-line OFRMPC approach in [152] based on a look-up table scheme is designed to reduce computational burden.

C. OFRMPC for Linear Systems With Norm-Bounded Uncertainty and Bounded Disturbances

For linear systems with norm-bounded uncertainty and bounded disturbances, an OFRMPC procedure in [153] consists of an off-line optimization where the feedback controller gain and state observer gain are designed via off-line BMIs and used to robustly stabilize augmented states. The on-line moving horizon OFRMPC optimization in [153] introduces additionalN(N≥1) perturbation items via the S-procedure,where the number of constraints increases linearly with control horizons. An OFRMPC approach with partial state measurements is investigated in [154], where an initialization phase is devoted to determining an admissible linear memoryless controller. Then, in the on-line stage, predictive capabilities complement the designed controller by means ofNsteps free control actions in receding horizon fashion.

The observer and controller gains of the OFRMPC approach in [155] are simultaneously optimized via the cone complementarity linearization approach. In [155], the estimation error sets calculated respectively from closed-loop system and estimation error system are compared to ensure recursive feasibility.By assuming that the system parameters have special structure, a convexity optimization to OFRMPC approach is further designed in [156] to reduce the computational burden. In[157], the estimator dynamic matrix is optimized to reduce computational burden and enhance control performance. By taking a linearization method similar to that in [158], the estimator dynamic matrix, estimator gain, and feedback gain are simultaneously on-line optimized in [159] to improve control performance.

IV. RELATIONSHIPS BETWEEN DIFFERENT OFRMPC APPROACHES

Different forms of OFRMPC approaches are summarized and classified in Sections II and III. Furthermore, the related OFRMPC approaches with different optimizations and estimation error sets are outlined in Table I. In this section, the relationships between different kinds of OFRMPC approaches are discussed and compared.

A. Relationships Between Dynamic and Observer-Based OFRMPC for Quasi-LPV (T-S Fuzzy) Systems

For quasi-LPV and T-S fuzzy systems, dynamic OFRMPC approaches can be of the parameter-dependent form as in (8),where the weighting functions (or membership functions)λl(k),l∈I[1,L], that are dependent on the scheduling parameter(or premise variable) θkshould be available at the current sampling timek. Then, by employing the techniques of RPI sets and LMIs, non-convex dynamic OFRMPC optimizations for quasi-LPV systems or T-S fuzzy systems can be formulated as SDP to simultaneously obtain all dynamic output feedback controller parameters. By taking dynamic output feedback controller, more freedoms for OFRMPC optimizations are introduced and all the dynamic output feedback controller parameters can be optimized via SDP optimizations.Most of dynamic OFRMPC optimizations with parameter-dependent controller parameters are solved via min-max optimizations to stabilize augmented closed-loop systems within one common RPI set. For OFRMPC optimizations, if the conservativeness in system parameters is mitigated, it will be advantageous for improving control performances. However,the exactly known LPV system parameters at each sampling time in min-max optimizations are often not exploited in dynamic OFRMPC, which are conservative in the optimized controller parameters.

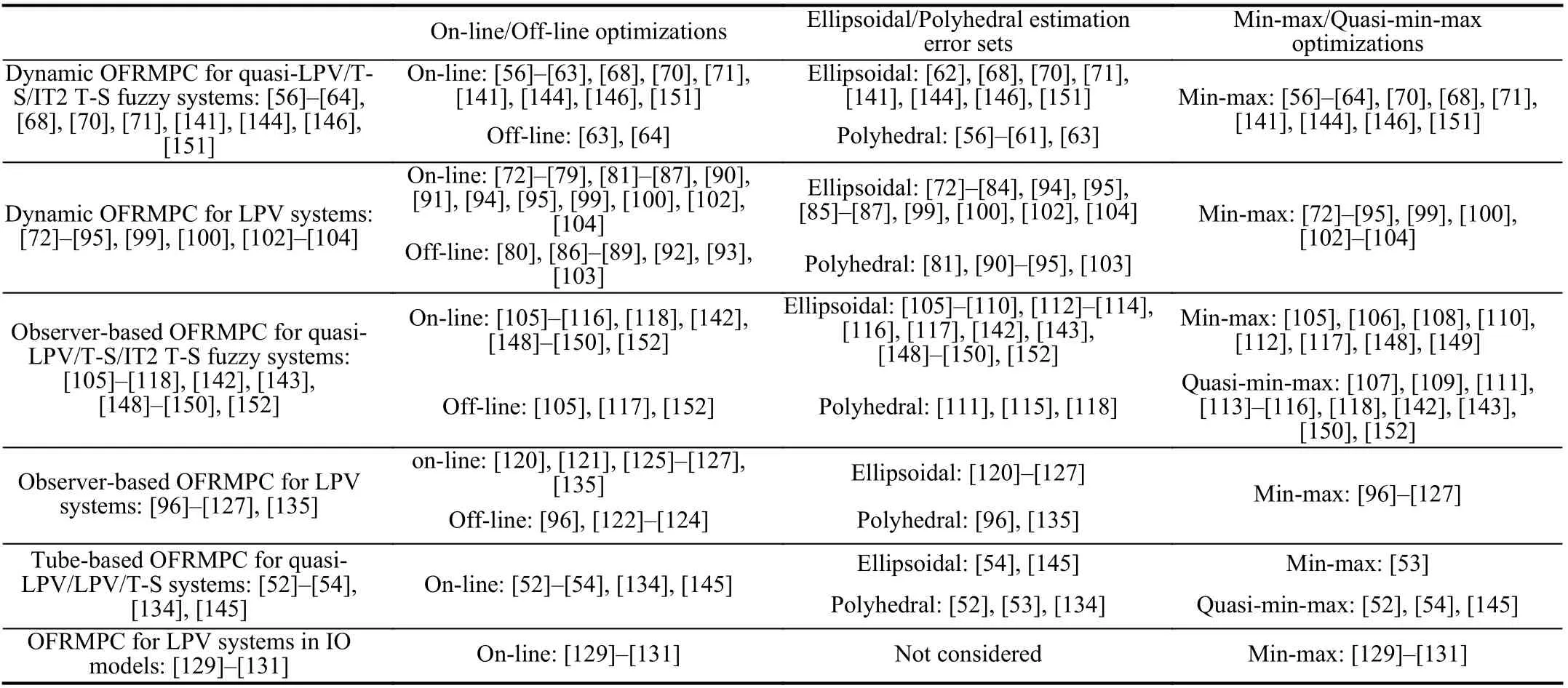
TABLE I COMPARISONS OF DIFFERENT OFRMPC APPROACHES

For quasi-LPV or T-S fuzzy systems, the augmented closedloop systems can be combined by autonomous estimation error systems and closed-loop observer systems steered by control inputs. Then, it is possible to consider observer-based OFRMPC approaches that synthesize the off-line optimization to design state observer gains and the on-line optimization to obtain controller gains (e.g., [105]–[108]), or simultaneously optimize observer gains and controller gains (e.g.,[112], [115]–[117]). It is also possible to incorporate the scheduling parameters of LPV systems into observer-based OFRMPC optimizations to formulate quasi-min-max OFRMPC optimizations (e.g., [115] and [116]). Furthermore,dynamic or observer-based OFRMPC for quasi-LPV and T-S fuzzy systems can be extended to OFRMPC for IT2 T-S fuzzy systems.

For dynamic OFRMPC, the formulated augmented closedloop systems are often constructed via system true states and controller states, which often complicate the proof of recursive feasibility for OFRMPC optimizations. For observerbased OFRMPC, when estimation error systems are convergent, it is often easy to stabilize the controlled LPV systems by ensuring robust stability of closed-loop observer systems.In this case, estimation error bounds can be properly handled by time-varying and non-increasing RPI sets. Then, the stabilization of controlled LPV systems can be realized by guaranteeing that closed-loop observer systems and estimation error systems are convergent within time-varying and non-increasing RPI sets. For observer-based OFRMPC, when the current scheduling parameter of LPV systems is available, the exactly known LPV system parameters at the current time can be considered in quasi-min-max OFRMPC optimizations to reduce the conservativeness of control inputs and improve control performance (e.g., [115] and [116]).

In [104] and [144], for LPV and T-S fuzzy systems, one free control input and one free controller state are introduced to dynamic OFRMPC approaches. One free control input is directly optimized for the observer-based OFRMPC approaches in [109] and [142]. Compared with [104] and [144], the optimized control inputs in [109] and [142] are less conservative and easy to reach the boundaries of control input constraints. The dynamic OFRMPC with multi-step closed-loop predictions in [76] and [146], and the dynamic OFRMPC with periodic invariant sets in [70] have not fully exploited the available system parameters at the current time, and therefore the optimized control inputs are not likely to reach the boundaries of input constraints. The quasi-min-max OFRMPC optimizations in [107], [115], [116], and [152] consider the exactly known system parameters at each sampling time such that the conservativeness of control inputs is reduced.

B. Relationships Between Dynamic and Observer-Based OFRMPC for LPV Systems

The relationships between dynamic OFRMPC in Section IIB and observer-based OFRMPC in Section II-D are discussed in [77]. By comparing the dynamic OFRMPC approach in [72]with the observer-based OFRMPC approach in [96], it is shown that there are no intrinsic differences between them.For an LPV system with unknown scheduling parameters,both dynamic and observer-based OFRMPC approaches can be designed. Since the non-convex BMI constraints resulting from OFRMPC optimizations are often introduced, the OFRMPC optimizations for LPV systems are complex. The main difficulty is to formulate convex optimizations to design controller parameters in dynamic OFRMPC and observer/controller gains in observer-based OFRMPC. In Section II-B, the solutions to dealing with non-convex BMI constraints for dynamic OFRMPC optimizations are summarized, i.e., 1) reformulation of non-convex BMIs as convex LMIs, and 2) design of off-line dynamic OFRMPC approaches. In Section II-D, the state observer gains in [120]–[122], [124] and [126] are offline given, and the controller gains are optimized. The state observer gains and controller gains in [125] and [127] are online simultaneously optimized via the technique of convexity approach to reformulate BMIs as LMIs. The summarized solutions to dealing with non-convex BMIs in OFRMPC optimizations are also summarized in Section VIII-A.

For LPV systems with unknown scheduling parameters,since the system parameters at the current and future time are uncertain, the formulated OFRMPC optimizations are often more conservative than those for quasi-LPV or T-S fuzzy systems. When both estimated states (or controller states) and estimation errors are bounded within RPI sets (e.g., [75], [88],[89]), the OFRMPC optimizations are often not easily made to be feasible, or their feasible regions are small. In [90], [91],[94], and [95], since the refreshment of estimation error bounds cannot employ the information on the current LPV system scheduling parameters, it is often complex to update the estimation error sets for dynamic OFRMPC with polyhedral estimation error sets.

C. Relationships Between Observer-Based and Tube-Based OFRMPC for Quasi-LPV (T-S Fuzzy) Systems

For observer-based OFRMPC, there exist three systems: the controlled LPV system (1) and (2), state observer system (15),and estimation error system (16). Robust stability of the controlled system is often realized via the stabilization of the estimation error system and closed-loop observer system, which is related to the synthesis of the state observer gain and controller gain. Tube-based OFRMPC approaches often involve the controlled LPV system (1) and (2), state observer system(22), nominal LPV system (23), estimation error system (26),and control error system (27). The state observer gain and ancillary feedback controller gain can guarantee that estimation errors and control errors are bounded and stabilized in RPI sets. The control input in (24) is composed of the nominal control input and the feedback term based on the real-time control error. In tube-based OFRMPC, the nominal control input is on-line optimized to stabilize the nominal system,where estimation errors and control errors are bounded within time-varying robust tubes.

Observer-based OFRMPC approaches are proposed in [109]and [142] with one-step open-loop prediction and one free control move, and in [115], [116], and [118] with one-step closed-loop system prediction, and in [107] with multi-step closed-loop predictions. At the current sampling time, since one free control move instead of feedback controller gain is directly optimized in [109] and [142], it is often difficult to design the RPI set for the current estimated state. Although the RPI sets for the current and future estimation errors can be known at each sampling instant, it is difficult to handle the state constraints at the current time. In [107], [115], [116], and[118], since the current and future feedback controller gains related to Lyapunov matrices are optimized in observer-based OFRMPC optimizations, it is easy to consider state constraints via the technique of RPI sets for the estimation error system and closed-loop observer system (see the details in Section VII-B). Differently from the observer-based OFRMPC approaches with one free control input in [109] and[142], the tube-based OFRMPC approaches in [52], [54] and[145] optimize one free nominal control input. The state constraints are considered in [54] and [145] by dealing with the bounded sets for the nominal state, estimation error and control error. Furthermore, observer-based OFRMPC approaches often guarantee that closed-loop systems are convergent within RPI sets, where real-time estimated states and estimation error bounds are considered in the formulated OFRMPC optimizations. For the tube-based OFRMPC approaches in[54] and [145], real-time estimation error bounds are constrained within the searched off-line computed robust tubes.Consequently, it is not required to consider real-time estimation error constraints in the on-line quasi-min-max OFRMPC optimizations.

V. CONSTRAINTS ON BOUNDED DISTURBANCES AND/OR NOISES AND CURRENT SySTEM STATES

The OFRMPC optimizations reviewed in this survey mainly include the constraints on bounded disturbances and/or noises,current system states, robust stability, control inputs, system states and outputs. In the following Sections V–VII, the methods of treating the constraints for different OFRMPC approaches are discussed.

A. Constraints on Bounded Disturbances and/or Noises

When the system parametersDandEare kept unchanged,the feasible regions of OFRMPC optimizations are related to the amplitudes of disturbances and noises. This means that smaller amplitudes of disturbances and noises are advantageous for larger feasible regions of OFRMPC optimizations.Larger amplitudes of disturbances and noises will, however,decrease the feasible regions or even lead to infeasibility of OFRMPC optimizations. Hence, for dynamic or observerbased OFRMPC approaches, when the amplitudes of disturbances and noises are large, the feasible regions for controller states or estimated states are small or even do not exist; for tube-based OFRMPC approaches, the robust tubes for estimation errors and control errors will be large such that the tightened constraint sets for nominal control inputs and nominal states will be small or even empty. For the observer-based OFRMPC approaches in [105]–[107], larger amplitudes of bounded disturbances and/or noises result in a larger minimal RPI set for estimation errors and a smaller feasible region for estimated states.

To ensure large feasible regions for OFRMPC optimizations, when the amplitudes of disturbances and/or noises are large, it is often required to tune the matricesDandEsuch that their elements are sufficiently small. Furthermore, for different amplitudes of disturbances and noises, it is possible to tune the elements of system parametersDandEsuch thatw(k)=v(k)holds. Then, it is convenient to employ the technique of quadratic boundedness to derive robust stability conditions. Furthermore, let ω(k)≜[w(k)T,v(k)T]Twithω(k)∈E(Pwv) andPwv=diag{0.5Pw,0.5Pv}. Then, the technique of quadratic boundedness can also be utilized to formulate robust stability conditions, but the conservativeness is introduced when the constraints on disturbances and noises are bounded within an augmented ellipsoidal set. For example, the disturbances and noises in [116] are the augmented vectors and bounded within an ellipsoid with a higher dimension, which introduces the conservativeness in dealing with bounded disturbances and noises. Disturbances and noises can be assumed to be the augmented form in (30), but it is suggested to separately deal with the constraints on disturbances and noises.

Note that the kinds of constraint sets for disturbances and/or noises can affect the process of updating estimation error bounds. When real-time estimation error bounds are updated,it has to perform set operations to deal with different forms of the constraint sets for bounded disturbances and/or noises. To update polyhedral estimation error bounds, the set operations between polyhedral estimation error sets and bounded ellipsoidal or polyhedral disturbances and/or noises are involved.To refresh ellipsoidal estimation error bounds, the set operations between ellipsoidal estimation error sets and ellipsoidal disturbances and/or noises are often required. In [58]–[61], to update polyhedral system state sets, the outer approximation of ellipsoidal bounded disturbance sets via polyhedral sets with vertices representation is required. Then, according to the estimation error systems, the vertices of true state bounds at the next sampling time are computed. In [62], [74], [75], and[85], the ellipsoidal estimation error sets are computed by employing the S-procedure to simultaneously consider ellipsoidal estimation error sets and disturbance sets. In [115], the bounded sets for disturbances and noises are represented as zonotopes, and the zonotopic set-membership state estimations are applied to update polyhedral estimation error sets.The update of polyhedral estimation error sets in [115] does not require the outer approximation of ellipsoidal constraint sets for disturbances and noises. Nevertheless, the robust stability and state constraints in [115] consider the outer approximations of bounded zonotopic disturbances and noises sets via ellipsoids.

In some cases, the constraint sets for disturbances and noises should be restricted in special forms. For example, to compute the minimal polyhedral RPI sets in [52] and polyhedral robust tubes in [134], it is assumed that disturbances and noises should be constrained within polyhedral sets. For the OFRMPC approach in [52], efficient tools for computing minimal polyhedral RPI sets are employed; for the OFRMPC approach in [134], polyhedral robust tubes are formulated as linear constraints in an OFRMPC optimization via quadratic programming.

B. Constraints on Current System States

At each sampling time, the current system states in OFRMPC are unknown. Hence, system state bounds are often utilized to represent uncertain system states. Dealing with unknown system state bounds is crucial for OFRMPC optimizations. System state bounds have the effects not only on control performances, but also on recursive feasibility of OFRMPC optimizations. To describe unknown current system states, it is often assumed that current system states are constrained within bounded convex sets. Different kinds of convex sets, such as polyhedral sets, ellipsoidal sets, and zonotopes, can be used to represent the current system states.For the augmented closed-loop systems in Section II, dealing with the constraints on augmented states is equivalent to the consideration of the current system state constraints. In this section, the methods of dealing with the constraints on the current system states are given.

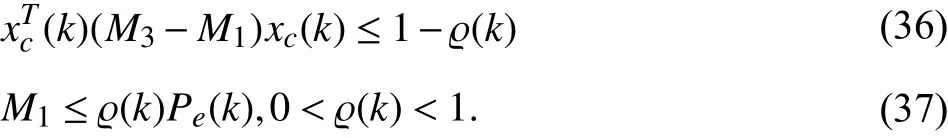
In (37), the ellipsoidal estimation error constraint is realized via the set , where the sets

. For dealing with the current system state constraints in dynamic OFRMPC with ellipsoidal estimation error sets, readers are referred to [62], [70], [72]–[82], and [85].

E(M1(k)/ϱ(k)) E(Pe(k))⊆E(M1(k)/ϱ(k))

The estimation error constraints in (35) and (37) may introduce conservativeness in dealing with the current system state constraints since larger ellipsoidal sets have to be considered to deal with estimation error bounds. To utilize a full Lyapunov matrix and introduce more freedoms for dynamic OFRMPC optimizations, the estimation errors in [64], [68],[70], [76], [79], and [81] are defined as ,where the transformation matrix is exactly known and updated at each sampling time.

e(k)≜x(k)-U(k)xc(k)U(k)

For dynamic OFRMPC with polyhedral state sets (e.g.,[61]), controller states are not necessary to be the centers of state constraint sets with the evolutions of system state bounds, which may introduce additional difficulties in updating system state bounds and the conservativeness in dealing with state constraints. If controller states are not at the centers of state constraint sets, the state constraint sets are often not center symmetric with controller states. Then, it will be difficult to perform set operations to obtain estimation error bounds. Furthermore, if state constraint sets are not the center symmetric with controller states, conservativeness is introduced in dealing with state constraints via ellipsoidal RPI sets.For dynamic OFRMPC with ellipsoidal estimation error sets,controller states are always at the centers of the current system state constraint sets. For the observer-based OFRMPC in Section II-D, the estimated state and estimation error constraints cannot be separately treated due to a full dimensional Lyapunov matrix and the coupling between the state observer system and estimation error system. Consequently, the constraints on the current augmented states composed of estimated states and estimation errors are directly handled (e.g.,[96], [153]).

3) Current System State Constraints for Tube-Based OFRMPC:For the tube-based OFRMPC in Section II-E, since the constraint sets for the nominal system, estimation error system and control error system are computed in off-line optimizations, the real-time constraints on the current system state in (25) can be handled by satisfying the constraints on the nominal state, estimation error and control error. Suppose that at the initial timek=0,

VI. CONDITIONS ON ROBUST STABILITy

When the current system states, bounded disturbances and/or noises are constrained within constraint sets, it is required to derive robust stability conditions to stabilize closed-loop systems. This section mainly reviews robust stability constraints for different OFRMPC approaches. For systems with bounded disturbances and/or noises, robust stability means that system states are stabilized within a region in the neighborhood of the origin. For LPV systems with bounded disturbances and/or noises, the techniques of quadratic boundedness (QB) in [65] and [66], and RPI sets are often employed to derive robust stability conditions. In Section VI-A, for dynamic OFRMPC approaches in Sections II-A and II-B, the processes on how to obtain robust stability conditions via the technique of QB are summarized. The robust stability conditions for the observer-based OFRMPC in Sections II-C and II-D can also be obtained via the technique of QB. Here, we omit the details for brevity. In Section VI-B, by applying the S-procedure, the RPI sets for augmented closedloop systems can be derived. In Section VI-C, the optimality conditions for closed-loop systems are derived.

A. RPI Sets for Dynamic OFRMPC Via QB

With a larger complexity parameter, less conservative sufficient constraints and a larger number of LMIs can be obtained at the cost of increasing computational burden. In the sequel,double convex combinations are also involved in the constraints on system states and outputs in Section VII.

B. RPI Sets for Closed-Loop Systems Via S-Procedure

In Section V-A, the technique of QB is employed to develop RPI sets for the augmented closed-loop systems (9) and (12).The technique of QB can also be employed to obtain robust stability conditions for systems (14), (16), and (19). For example, the sub-observer gains with the minimal RPI set for estimation errors in [105] are off-line optimized via the technique of QB. Then, in the on-line OFRMPC optimization, the closed-loop system (14) is robustly stabilized via the technique of QB. By employing the technique of S-procedure, the sufficient RPI conditions for closed-loop systems are also directly formulated in dynamic OFRMPC (e.g., [85]) and observer-based OFRMPC (e.g., [116]). Here, we take system(12) as an example to show that by directly employing the Sprocedure, the robust stability conditions in (53) can also be deduced. The main procedures can be summarized as follows:

According to system (15) and the Schur complement, condition (60) is guaranteed by (62).

For the conditions in (61), the scalar κ1∈(0,1) is often prespecified, and the non-negative scalars κ2and κ3are the online decision variables. In [106], [107], and [115], the observer gains are off-line optimized. Then, by applying the S-procedure, the on-line OFRMPC optimizations ensure that the closed-loop observer systems are bounded in time-varying RPI sets. In [116] and [117], the RPI conditions for augmented closed-loop systems are obtained via the S-procedure,which also imply that estimated states and estimation errors are bounded within the corresponding RPI sets.

C. Optimality Conditions for Closed-Loop Systems

By employing the techniques of QB or S-procedure, the RPI sets for closed-loop systems can be derived, which also imply that nominal closed-loop systems are convergent within the RPI sets. Here, the nominal augmented closed-loop systems are the closed-loop systems without bounded disturbances and noises. For example, when bounded disturbances in system(12) are not involved, the nominal closed-loop system is

The observer-based min-max OFRMPC approaches in [105]and [106] ensure that the current and future estimation error sets (closed-loop observer systems) are bounded within one common RPI set. The robust stability conditions in [105] also imply that the nominal estimation error system and nominal observer system are steered to the origin such that the controlled system is stabilized in a neighborhood of the origin due to bounded disturbances.

For the observer-based min-max OFRMPC approach in[106], theH∞-type cost function in (69) consists of the predicted estimated states, control inputs, and estimation errors.Furthermore, the parameterτcan be on-line optimized to account for real-time estimation error bounds and their influences on the control performance.

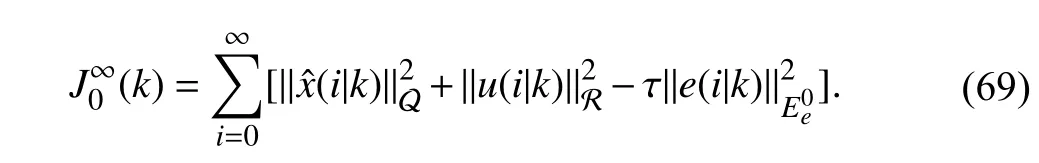
Therefore, by considering quasi-min-max OFRMPC optimizations, the system parametric uncertainties at the current time are reduced such that the optimized control inputs are easy to reach the boundaries of input constraints, which is advantageous for improving the control performance. For the tube-based OFRMPC approaches in [52]–[54], [134], and[145], the estimation errors and control errors are bounded in minimal RPI sets or time-varying robust tubes. Then, nominal control inputs are optimized to ensure that nominal systems are robust stable. Furthermore, the quasi-min-max tube-based OFRMPC optimizations in [52], [54], and [145] exploit the information on the current system parameters and reduce the conservativeness in OFRMPC optimizations.

VII. CONSTRAINTS ON CONTROL INPUTS, SySTEM STATES AND OUTPUTS

Based on the constraints on the current system states, disturbances and/or noises in Section V, and the robust stability conditions in Section VI, it is possible to deal with physical constraints in OFRMPC optimizations. Different OFRMPC optimizations can employ different methods to deal with physical constraints. For OFRMPC via the stabilization of closedloop systems, the techniques of dealing with physical constraints are related to the RPI sets for closed-loop systems. By properly considering the bounds on the affine transformations of RPI sets, physical constraints can be treated. In this section,for different OFRMPC optimizations, the methods of handling the constraints on the control inputs, system states and outputs respectively in (3)–(5) are discussed.

A. Constraints on Control Inputs

In [115] and [116], the current and future control input constraints take the similar form as in (74), but the bounded constraint sets for the current and future estimated states are respectively optimized. For the observer-based OFRMPC approaches in [109] and [142], the constraints on the current one free control input are directly treated to be componentwise bounded, and future control input constraints have the similar form as in (74). For the observer-based OFRMPC approaches in [96] and [121], although the control inputs are based on the feedbacks of estimated states, the control input constraints are related to the constraint sets for augmented states since the augmented closed-loop systems in [96] and[121] cannot be separated into estimation error system and closed-loop observer system. In Section II-F, for the OFRMPC approaches represented as LPV systems in the IO form, the control input constraints have the similar form as in(74), where the RPI sets for the augmented states composed of the current and past system inputs and outputs are involved.

3) Control Input Constraints for Tube-Based OFRMPC:For the tube-based OFRMPC approaches in [52], [54], and [145],the control inputs in (24) are combined via the feed-forward partu¯(k) and the feedback partu˜(k). In [52], the feed-forward partu¯(k) is componentwise bounded within the tightened constraint set for nominal control input; the constraints on the future nominal control inputs are related to the time-varying terminal RPI sets for nominal states; the feedback partu˜(k) is the affine transformation of the minimal polyhedral RPI set for the control error via an ancillary feedback controller gain.In [53], the nominal controller gains are optimized to stabilize the nominal system. The nominal control inputs with the tightened constraints in [53] have the similar form as in (74),where the affine transformations of the RPI sets for the nominal system via nominal controller gains are considered.

B. Constraints on System States

In Section V-B, the system state constraints at the current time for different OFRMPC are given. In the sequel, based on the RPI sets for augmented states, estimated states, estimation errors and control errors, the state constraints in different OFRMPC approaches are discussed.

1) System State Constraints for Dynamic OFRMPC:In Sections II-A and II-B, the prediction models for system states are related to the augmented closed-loop systems (9) and (12).Here, we take system (12) as an example. The system state prediction model according to system (12) is

In [96], the method of dealing with state constraints is similar to those in [116]–[118], but a full dimensional Lyapunov matrix and matrix inequalities are exploited. In [109] and[142], the state constraints are not explicitly considered. However, the predicted estimated states and estimation errors are assumed to be convergent within RPI sets. In [106], the current and future estimated states (estimation errors) are bounded within RPI sets, where set summation of the RPI sets for the initial estimation state and estimation error satisfies state constraints. Furthermore, the reduction of the conservativeness in state constraints can enlarge feasible regions for OFRMPC optimizations. For dynamic OFRMPC approaches in [68] and [76], by considering the relaxation scalars to reduce the conservativeness in state constraints, the feasible regions of OFRMPC optimizations are enlarged. For the online observer-based OFRMPC approaches in [107], [115],[116], [118], and [152], the state constraints also consider the exactly known system parameters at the current time such that larger feasible regions are obtained. Compared with the offline OFRMPC algorithm in [105], the feasible region of the off-line OFRMPC approach in [117] is enlarged by reducing the conservativeness in dealing with state constraints.

3) System State Constraints for Tube-Based OFRMPC:

According to the definition of the system state in (25), if the constraints on the nominal state, control error and estimation error at each timek≥0 are properly treated, the state constraints can be satisfied. At each timek≥0, suppose that

C. The Constraints on System Outputs

In OFRMPC optimizations, either system output or state constraints are considered. In general, it is not necessary to simultaneously consider all system state and output constraints. In some cases, it is possible to simultaneously consider constraints on partial system states and system outputs(e.g., [76], [81], [83]). To deal with system output constraints,it is often assumed that the system matrixC(θk) in (2) is composed ofnyrows ofnx- dimensional identity matrix (ny≤nx),and the matrixE(θk) can tune the amplitudes of bounded noises. Then, in some cases, system outputs are equivalent to partial measurable system states (i.e., the matrixE(θk)=0).System outputs can be related to partial system states with bounded noises (i.e., the matrixE(θk)≠0). The methods of dealing with system state and output constraints are the similar, where different closed-loop systems result in different constraints on system outputs. For example, for the closedloop system (12) in dynamic OFRMPC, the system output constraints in (5) are guaranteed by

According to the techniques in [68], [76], [78], [83] and[96], the conservativeness of dealing with system outputs in(90) can be further reduced. For the observer-based OFRMPC,the methods of dealing with system output constraints and reducing their conservativeness are similar to the dynamic OFRMPC. In OFRMPC for LPV systems with IO forms, the system output constraints in [129]–[131] are complex since input delays should be further considered.

From the above discussions on physical constraints, the constraints on control inputs, system states and outputs are often related to the affine transformations of ellipsoidal RPI sets for closed-loop systems, controller states (or estimated states),and bounded disturbances and/or noises. Then, the componentwise constraints on the affine transformations of different ellipsoidal RPI sets are enforced. Furthermore, different techniques can be exploited to reduce the conservativeness in dealing with physical constraints. However, the constraint sets for control inputs, system states and outputs are often polyhedral sets (e.g., the polyhedral constraint sets in (3)–(5)). When ellipsoidal RPI sets and their affine transformations are bounded within polyhedral sets, the conservativeness in dealing with physical constraints is often introduced.

VIII. KEy ISSUES ON OFRMPC FOR LPV SySTEMS

In summary, although the aforementioned works on OFRMPC have many differences, such as state observer systems, closed-loop systems, robust stability and physical constraints, there are key issues that are mainly concerned. In this section, key issues on the reviewed OFRMPC approaches for LPV systems are pointed out.

A. Dealing With Non-Convex BMIs

For uncertain systems represented as LPV systems, the design of OFRMPC approaches often results in difficulties of solving non-convex BMIs optimizations. To reformulate BMIs as convex LMIs, the following methods of dealing with BMIs for different OFRMPC optimizations are summarized.

1) Parameter-Dependent Controller Parameters:For quasi-LPV or T-S fuzzy systems, controller parameters in dynamic OFRMPC optimizations can take the parameter-dependent form in (8). Then, by taking the techniques of LMIs, BMI constraints in robust stability conditions are reformulated as LMIs such that OFRMPC with convex optimizations is solved to simultaneously obtain all dynamic output feedback controller parameters (e.g., [58]–[62], [64], [68], [70], [141]).

2) Synthesis of Off-Line State Observer Gain and On-Line Controller Gain:For quasi-LPV or T-S fuzzy systems, observer-based OFRMPC approaches can synthesize the off-line optimized state observer gain and on-line feedback controller gain. Then, BMI optimizations resulting from simultaneously optimizing the state observer gain and controller gain can be avoided (e.g., [71], [105]–[107], [109], [111], [113]–[115],[118], [142], [149], [152]). In [96]–[126], the observer gainL0in systems (17) and (20) is pre-specified, and the OFRMPC optimizations can be formulated as LMI constraints and solved as SDP optimizations.

3) Cone Complementarity Linearization Approach:For LPV systems with unknown scheduling parameters, dynamic OFRMPC optimizations often involve dynamic output feedback controller parameters and mutual inverse matrices required to be simultaneously optimized (e.g., [72], [73], [79], [91], [94]).By employing the cone complementarity linearization approach in [97] to iteratively minimize a performance index with mutual inverse matrix variables, dynamic output feedback controller parameters with minimal performance index are optimized. The iterative cone complementarity linearization approach often leads to heavier computational burden, and is not suitable for on-line OFRMPC optimizations.

A variant cone complementarity linearization approach in[158] simplifies the iteration procedure in [72] and reduces the computational burden. The linearization method in [158] is extended to an OFRMPC approach for norm-bounded linear systems with disturbances in [159]. To reduce the computational burden resulting from cone complementarity linearization approach, the off-line OFRMPC approaches in [80], [88],[89], [92], [93], and [103] design look-up tables for searching real-time controller parameters. Then, the computational burdens of the cone complementarity linearization approach are removed into off-line optimizations.

4)Partial Dynamic Output Feedback Controller Parameters Pre-Specified in Off-Line Optimizations:For LPV systems with unknown scheduling parameters, non-convex dynamic OFRMPC optimizations are often involved when all dynamic output feedback controller parameters (e.g., parameters {Ac(k),Lc(k),Fx(k),Fy(k)} in (10) and (11)) are simultaneously optimized. In [74]–[77] and [94], to reformulate nonconvex dynamic OFRMPC optimizations as convex optimizations, at the initial timek=0, dynamic output feedback controller parameters {Ac(0),Lc(0),Fx(0),Fy(0)} are optimized via the cone complementarity linearization approach. Then, at timek≥0, by pre-specifying the partial parametersLc(k)=Lc(0) andFy(k)=Fy(0), and employing the techniques of LMIs, the other parameters {Ac(k),Fx(k)} at timek≥0 can be optimized via SDP optimizations when dynamic OFRMPC optimizations are solved.

5) Special Assumptions on System Parameters:By making some proper assumptions on system structure, it is possible to reformulate BMIs into LMIs. In [84], [99], [100], [127], and[132], it is assumed that the system matrices related to measurements are full row rank. Then, convex OFRMPC optimizations are formulated and solved as SDP optimizations to simultaneously optimize observer and controller parameters.

6) Utilizations of Matrix Inequalities:In [85], by employing the technique of the Young’s inequality in [101], all dynamic output feedback controller parameters with the corresponding minimal performance index are simultaneously online optimized via convex optimizations. In [116], the BMIs problems resulting from simultaneously optimizing observer and controller gains are reformulated as LMIs via the technique of the Young’s inequality. For the designed look-up tables in [54] and [145], the technique of the Young’s inequality is employed to off-line simultaneously optimize a sequence of state observer gains and ancillary feedback controller gains.By further utilizing a relaxation formula and matrix inequality in [162], the convex dynamic OFRMPC optimization in[102] improves the OFRMPC method in [84].

B. Estimation Error Constraints and Bounds

Besides model parametric uncertainty, bounded disturbances and/or noises, uncertain estimation error bounds represent another source of system uncertainties. To guarantee robust stability and the satisfaction of physical constraints, timevarying estimation error bounds have to be handled, which complicates OFRMPC optimizations.

1) Handling of Estimation Error Constraints:In [56], [63],[90], [96], and [124], the estimation error constraints are treated analogously as the input/state constraints in OFRMPC optimizations. For dynamic OFRMPC optimizations without estimation error constraints (e.g., [58], [72]), the RPI sets for closed-loop systems guarantee that the augmented states are bounded and convergent within RPI sets. However, it does not imply that controller states and system state bounds are constrained within the corresponding RPI sets. If the controller state and/or estimation error constraints are further considered in dynamic OFRMPC optimizations (e.g., [75], [86]–[89], [99],[100]), the controller states and estimation errors are separately bounded within the corresponding RPI sets.

For off-line dynamic OFRMPC, when estimation error constraints are considered, it is advantageous for guaranteeing the satisfaction of estimation error constraints for real-time searched dynamic controller parameters. In off-line OFRMPC approaches (e.g., [86], [88], [89], and [96]), since estimation error constraints are considered in off-line optimizations, realtime estimation error constraints are always guaranteed in the on-line searching stage. For the off-line OFRMPC with polyhedral estimation errors in [93], the searched real-time controller parameters correspond to time-varying estimation error bounds and the regions of attraction with the closest containment of real-time controller states.

It is often suggested that additional estimation error constraints are not to be considered in on-line dynamic OFRMPC optimizations. Since robust stability of the augmented closedloop systems is considered in OFRMPC optimizations, augmented closed-loop system states are bounded and convergent within on-line optimized time-varying RPI sets. Then, the estimation error defined as the differences between true state and controller state will be bounded within the related timevarying constraint sets. At each sampling time, time-varying estimation error sets can be updated via the separate on-line auxiliary optimizations when OFRMPC optimizations are solved. If additional estimation error constraints are considered in on-line dynamic OFRMPC optimizations, it will not only increase on-line computational burden, but also affect feasible region and control performance. For on-line dynamic OFRMPC approaches with polyhedral estimation error sets(e.g., [56]–[60], [90], [91], [94], [95]) and ellipsoidal estimation error sets (e.g., [62], [70]–[79], [82]–[85]), the estimation error bounds are updated in separate auxiliary optimizations.Both polyhedral and ellipsoidal estimation error sets are considered in [61], [81], [103], and [115]. By properly updating estimation error bounds and ensuring that closed-loop system states are bounded and convergent in RPI sets, robust stability of the controlled LPV systems can be satisfied.

For observer-based OFRMPC, estimated states and estimation errors are constrained in time-varying RPI sets. In these cases, it is not required to consider estimation error constraints in OFRMPC optimizations. Nevertheless, the estimation error constraints can be RPI sets by scaling the minimal RPI set for estimation errors (e.g., [105]–[107], [152]) or realtime optimized estimation error sets (e.g., [87], [100], [116]).For the tube-based OFRMPC approaches in [52]–[54] and[145], the real-time estimation errors are constrained within the robust tubes for estimation errors (e.g., polyhedral robust tubes in [52] and [53], and nested ellipsoidal robust tubes in[54] and [145]). The on-line OFRMPC optimizations in[52]–[54] and [145] with tightened constraints are solved to stabilize nominal systems, where estimation errors are bounded within robust tubes.

2) Update of Estimation Error Bounds:For quasi-LPV systems, the methods of updating polyhedral estimation error sets for the dynamic OFRMPC approaches in [56]–[60] are discussed in Section II-A. For LPV systems with unknown scheduling parameters, the methods of updating polyhedral estimation error sets for dynamic OFRMPC approaches in[90]–[95] are given in Section II-B. For the dynamic OFRMPC approaches in [61], [81], and [103], to ensure recursive feasibility and reduce the conservativeness in updating estimation error bounds, polyhedral and ellipsoidal estimation error sets are respectively computed according to estimation error systems and the invariance of closed-loop systems.Then, if polyhedral estimation error sets are contained within the ellipsoidal one, less conservative polyhedral estimation error sets are obtained. For the dynamic OFRMPC approaches in [72], [73], [82]–[84], [158], and [163], recursive feasibility is guaranteed when ellipsoidal estimation error sets are updated via the invariance of closed-loop systems. For the dynamic OFRMPC approaches in [62], [68], [85], [141], and[151], to ensure recursive feasibility and reduce the conservativeness in updating ellipsoidal estimation error bounds, two ellipsoidal estimation error sets computed respectively from estimation error systems and the invariance of closed-loop systems are compared.

For quasi-LPV and T-S fuzzy systems, the estimation error systems in observer-based OFRMPC approaches are autonomous and separated from closed-loop observer systems. Thus,estimation error systems are only related to the current estimation error bounds and disturbances and/or noises. For the methods of updating estimation error bounds in observerbased OFRMPC approaches, readers are referred to [105]–[109], [116], [117], [142]–[144], [148]–[150] and [152].

3) The Relationships Between Estimation Error Bounds and Control Performances:For min-max OFRMPC approaches,all the possible realizations of parametric uncertainties, bounded disturbances and/or noises are incorporated in RMPC optimizations. Then, output feedback controller gains are related to the RPI sets for augmented states, estimated states and estimation error sets. According to the analysis in Section VII-A, the control inputs are related to the affine transformations of RPI sets for augmented states, estimated states, and bounded sets for disturbances and/or noises. When precise estimation error bounds are obtained, less conservative system state bounds can be estimated, which are advantageous for optimizing feedback controller gains and reducing the conservativeness in control inputs. For the OFRMPC with minmax optimizations in [58]–[60], [62], [74], [87], [93], and[141], by properly updating estimation error bounds at each sampling time, the control performances can be improved.

For the observer-based OFRMPC approaches with quasimin-max optimizations (e.g., [107], [109], [115], [116], [142],and [152]), the update on estimation error bounds will not have significant influences on control performances. In [109]and [142], one free control input is introduced such that the control input can reach the boundaries of control input constraints. Then, estimation error bounds will not have significant influences on the responses of closed-loop systems. In[107], [115], [116], and [152], the current and future estimated states (estimation errors) are bounded in different RPI sets. Furthermore, the LPV system parameters are exactly known at the current time and considered in MPC optimizations such that the conservativeness of optimized output feedback controllers is reduced. When the control inputs in [107],[115], [116], and [152] reach the boundaries of control input constraints, the capabilities of feedback controllers are fully exploited. As a result, the update of estimation error sets will not have obvious influences on control performances.

C. Recursive Feasibility and Robust Stability

In this section, by employing the technique of RPI sets for closed-loop systems, recursive feasibility and robust stability for different OFRMPC optimizations are discussed.

1) Dynamic OFRMPC Case:In [58]–[60] and [91]–[95], for the dynamic OFRMPC approaches with polyhedral estimation error sets, robust stabilization of closed-loop systems is guaranteed by ensuring that the current and future closed-loop states are bounded and convergent within one common RPI set. The robust stability of augmented states does not necessarily means that augmented state bounds are convergent within RPI sets. However, when the bounds of augmented states at the next sampling time are constrained within the RPI set, the feasibility of the OFRMPC optimization at the next sampling time is guaranteed. The auxiliary optimizations in[58]–[60], [90], [91], [94], and [95] are performed to not only update estimation error bounds, but also determine the feasibility of OFRMPC optimization at the next sampling time.The recursive feasibility of OFRMPC approaches in[58]–[60], [90], [91], [94], and [95] is not guaranteed in theory. In [61], recursive feasibility of dynamic OFRMPC with polyhedral estimation error sets is guaranteed by comparing the estimation error sets computed via the invariance of closed-loop system and estimation error system.

For dynamic OFRMPC approaches with ellipsoidal estimation error sets (e.g., [62], [68], [72], [73], [82]–[85], [141],[151], [158], [163]), recursive feasibility is satisfied by ensuring that the closed-loop system states are bounded within RPI sets. When controller state constraints are additionally considered (e.g., [75], [87], [99], [100]), the RPI sets for controller states and estimation errors can be optimized. In Section VIC, the RPI conditions for closed-loop systems imply that nominal augmented closed-loop systems are Schur stable. Therefore, when nominal closed-loop systems are convergent to the origin, the controlled LPV systems are stabilized to a region in the neighborhood of the origin.

2) Observer-Based OFRMPC Case:For observer-based OFRMPC, when augmented closed-loop systems are separated into closed-loop observer systems and estimation error systems (e.g., [105]–[118], [143], [148]–[150], and [152]),recursive feasibility of OFRMPC optimizations is guaranteed by stabilizing the closed-loop observer systems and estimation error systems within time-varying RPI sets. Then, robust stability of the controlled systems is satisfied by ensuring that the nominal closed-loop observer system and nominal estimation error are convergent to the origin. Meanwhile, the closedloop observer system and estimation error system are bounded in time-varying RPI sets. For the on-line OFRMPC approaches in [120], [121], and [125], since the estimation error systems are not autonomous, the methods of guaranteeing recursive feasibility and robust stability are similar to those in dynamic OFRMPC approaches.

3) Tube-Based OFRMPC Case:In [52]–[54] and [145],recursive feasibility and robust stability are ensured by steering nominal states to the origin, and the estimation errors and control errors are constrained within robust tubes. In [52] and[53], the estimation errors and control errors are bounded in minimal polyhedral RPI sets. Time-varying estimation errors and control errors in [54] and [145] are bounded within the searched robust tubes. In [52], [54], and [145], the nominal control inputs are optimized to ensure that the future nominal states are bounded within time-varying terminal constraint sets. In [52], terminal constraint sets are on-line optimized, but real-time scaled terminal constraint sets in [54] and searched terminal constraint sets in [145] are considered.

Note that it is not required to consider recursive feasibility for off-line OFRMPC approaches (e.g., [63], [64], [80], [88],[89], [92], [93], [96], and [103]). The searched real-time dynamic controller parameters, state observer gains and controller gains optimized in off-line optimizations can ensure that real-time controller states (estimated states) and estimation errors are convergent in the searched RPI sets.

D. Improvement on OFRMPC Control Performance

The control performance of OFRMPC is mostly related to reducing the conservativeness of control inputs in RMPC optimizations such that the capabilities of feedback controllers can be fully exploited. This section discusses the methods that can be utilized to reduce the conservativeness of control inputs.

1) Reducing the Conservativeness of Controller Parameters via Updating Estimation Error Bounds:To improve control performances, the methods of updating estimation error bounds are mostly applicable for OFRMPC with min-max optimizations. For min-max OFRMPC optimizations, the constraint sets for controller states and estimation error bounds are time-varying, where less conservative estimation error bounds can help to reduce the conservativeness of controller parameters. In Section VII-A, it is shown that the controller parameters are related to the affine transformations of the bounded constraint sets for augmented states, estimated states,bounded disturbances. For the min-max OFRMPC optimizations in [58]–[61], since feedback controller gains have the relationships with the RPI sets for constraining augmented states, less conservative estimation error bounds contribute to reducing the conservativeness of dynamic output feedback controller parameters. By precisely updating estimation error bounds, the control performance of the OFRMPC in [59] is better than that in [58]. By properly selecting the order of zonotopes and updating estimation error bounds, the control performance of the OFRMPC optimization in [60] is better than those in [58] and [61].

2) One Free Control Input and One Free Controller State for Dynamic OFRMPC:Differently from the observer-based OFRMPC approaches with one free control input in [109] and[142], where the separation between observer system and estimation error system and the observer gains exists, it is often complex to introduce free control input for dynamic OFRMPC. In [104] and [144], dynamic OFRMPC approaches with one free control input and one free controller state respectively for LPV and T-S fuzzy systems are introduced. Compared with the OFRMPC approaches in [72] and [141], the methods in [104] and [144] improve the control performances and enlarge the feasible regions. However, compared with the observer-based OFRMPC with one free control input in [109]and [142], although the conservativeness of control inputs is reduced, the control inputs in [104] and [144] are not easy to reach the boundaries of control inputs.

3) Multi-Step OFRMPC Optimizations:Multi-step dynamic OFRMPC approaches in [68] and [76], and multi-step observer-based OFRMPC approaches in [107] and [146] are designed to reduce the conservativeness of control inputs. The multi-step OFRMPC approaches in [68], [76], [107], and[146], and the dynamic OFRMPC approach with periodic invariant sets in [70] are developed based on multi-step closed-loop system predictions. The multi-step OFRMPC approaches in [68], [76], and [146] can enlarge feasible regions and improve control performances, but the scheduling parameter (or membership function) is not exploited and the exactly known system parameters at the current time are not considered in OFRMPC optimizations. The observer-based OFRMPC approaches with quasi-min-max optimizations in[115], [116], and [152] can be extended to multi-step observer-based OFRMPC approaches. The OFRMPC approaches with multi-step closed-loop predictions significantly increase on-line computational burdens when prediction horizons are large. The multi-step open-loop OFRMPC approaches with quadratic programming in [134] and [135] are designed,where terminal constraint sets are off-line designed and multistep control inputs are receding horizon optimized.

4) Saturated Control Inputs:The saturated control inputs can fully utilize the capabilities of output feedback controller parameters. Both the dynamic OFRMPC approaches in [75],[87], [99], [100], and [149], and the static OFRMPC approach in [132] adopt saturated control inputs to reduce the conservativeness of feedback controller gains. The saturated dynamic output feedback controller parameters in [75], [87], [99],[100], and [149], and the static output feedback controller gain in [132] are formulated as the convex hull involving actual output feedback controllers and auxiliary feedback controllers.In the on-line OFRMPC optimizations, only the constraints on auxiliary feedback controllers are involved, and the constraints on actual output feedback controllers are not directly considered. In [75], [87], [99], [100], [132], and [149],although control performances can be improved via adopting saturated control inputs, the on-line computational burdens increase since additional auxiliary feedback controller decision variables and more LMI constraints are introduced in online OFRMPC optimizations.

5) One Free Control Input for Observer-Based OFRMPC:

In [109] and [142], the infinite-horizon control inputs are parameterized as one free control input followed by an output feedback controller gain based on the pre-specified state observer gain. For the observer-based OFRMPC approaches in [109] and [142], free control inputs instead of feedback controller gains are directly optimized. The OFRMPC optimizations in [109] and [142] are the quasi-min-max optimizations, and the current exactly known system model parameters can be considered in OFRMPC optimizations. The optimized control inputs can reach the boundaries of input constraints.

6) Observer-Based OFRMPC With Quasi-Min-Max Optimization:In [115], [116], [118], and [152], the current and future output feedback controller gains are respectively related to the current and future constraint sets for the current and future closed-loop states. The current feedback controller gains in[115], [116], [118], and [152] are related to the RPI sets for constraining the current estimated states, which can be regarded as OFRMPC with one free feedback controller gain.The formulated quasi-min-max optimizations in [115], [116],[118], and [152] exploit the exactly known system parameters at the current sampling time, and consider that the current and future estimated states (estimation errors) are constrained within different RPI sets. Then, the control inputs are easy to reach the boundaries of input constraints and improve control performances.

7) One Free Nominal Control Input for Tube-Based OFRMPC:In [52], [54], and [145], the control input in (24) is constituted of the feed-forward part given by the tube-based model predictive controller (or one free nominal control input)and the feedback part based on the control error. The feedback part is related to the affine transformation of off-line control error sets via ancillary feedback controller gains. The one free control input in [52], [54], and [145] is a free decision variable, and can be directly optimized. By properly treating the tightened constraint sets for nominal states and nominal control inputs, as well as the bounded sets for estimation errors and control errors, the conservativeness in handling the constraints on nominal states and nominal control inputs can be reduced. The on-line quasi-min-max optimizations in [52], [54], and [145] exploit the exactly known system parameters at the current sampling time, and the nominal control inputs are optimized to steer nominal systems to the origin. The optimized control inputs have the tendencies to reach the boundaries of control inputs. However, when the estimation error sets and control error sets in [54] and [145]are enlarged, the control inputs in the tube-based OFRMPC approaches are difficult to reach the boundaries of control inputs. The reason is that the conservativeness is introduced when the affine transformation of the off-line control error sets via ancillary feedback controller gains is considered (i.e.,the feedback part in (24) bases on an off-line ancillary feedback controller gain).

According to the aforementioned methods of reducing the conservativeness in control inputs, for quasi-LPV (or T-S fuzzy) systems, the available scheduling parameter (or premise variable) can be employed not only to design parameter-dependent controllers in min-max OFRMPC optimizations, but also to consider the current exactly known system parameters in quasi-min-max OFRMPC optimizations. Since all the possible realizations of parametric uncertainties are considered in min-max OFRMPC optimizations, the current exactly known LPV system parameters are not fully exploited,which often introduces conservativeness in OFRMPC optimizations. For quasi-min-max OFRMPC optimizations, since the current and future closed-loop system states can be bounded within different RPI sets, it is possible to exploit the current exactly known system parameters in quasi-min-max OFRMPC optimizations. In general, for quasi-LPV systems,compared with min-max OFRMPC optimizations with parameter-dependent forms, it is advantageous for improving control performances by reducing the conservativeness of LPV system parameters in quasi-min-max OFRMPC optimizations.

E. Reduction of On-Line Computational Burden

OFRMPC optimizations for LPV systems are mostly formulated as min-max or quasi-min-max optimizations and solved as SDP optimizations. The algorithm complexities of solving SDP optimizations are associated with the numbers of LMI decision variables and LMI rows [164]. Hence, the computational burdens of OFRMPC optimizations increase with submodels of LPV systems, dimensions of system states, control inputs, and so on. The implementations of min-max or quasimin-max OFRMPC optimizations usually suffer from expensive on-line computational costs [37]. In this section, some methods of reducing the computational burdens of OFRMPC optimizations are summarized.

1) Off-Line Look-Up Table:Off-line OFRMPC approaches for LPV systems are mostly based on off-line designed lookup tables that save off-line computed controller parameters and related regions of attraction. Then, on-line controller parameters are searched according to real-time estimated states and estimation error bounds. The off-line OFRMPC problems are often min-max optimizations because of unavailable scheduling parameters of LPV systems in off-line OFRMPC optimizations. The off-line dynamic OFRMPC approaches in [63], [80], [93], and [157], and the off-line observer-based OFRMPC approaches in [105], [96], and [122]are studied. The off-line OFRMPC approaches with polyhedral estimation error sets in [93] and [96], and with ellipsoidal estimation error sets in [80], [105], and [122], and with both polyhedral and ellipsoidal system true state bounds in [64] and[103] are investigated. The off-line OFRMPC approach in[122] separately designs the estimator and controller gains,and ignores the interaction between the estimator and controller gains. Thus, the estimator/controller pair satisfying the robust stability of an augmented closed-loop system should be checked. The off-line OFRMPC approach in [123] improves the algorithm in [122]. The observer gains in [96] and subobserver gains in [105] are pre-specified, and time-varying controller gains are searched according to real-time estimated states and estimation error bounds.

Differently from the off-line OFRMPC approach in [122],the constraints on estimation errors are considered in the offline OFRMPC optimizations (e.g., [63], [88], [92], [93], and[96]), and the real-time searched controller parameters with guaranteed estimation error constraints are admissible. Furthermore, the off-line OFRMPC optimizations in [80], [93],[105], and [157] consider different bounds of estimation error constraints and can deal with time-varying estimation error sets in the on-line stage. For the off-line dynamic OFRMPC approaches in [64] and [103], polyhedral and real-time ellipsoidal true state bounds are utilized to refresh and tighten realtime state bounds, which are utilized for searching the suitable invariant sets with the closest containment of real-time estimated states. The work in [103] combines the merits of[80] and [81], and improves the control performance in [80].Different sizes of regions of attraction in [80], [93], [105],[96], and [157] cannot be guarantee to be nested in theory.The optimized regions of attraction in [117] are nested in theory, which are advantageous for searching real-time observer and controller gains. Furthermore, by setting the search steps in [117], the on-line computational burden resulting from searching observer and controller gains stored in the off-line look-up table is reduced.

2) One-Step Ahead OFRMPC:For the one-step ahead OFRMPC approach in [163], the current control input is computed by the controller parameters optimized at the previous sampling interval and implemented instantaneously. At the current sampling interval, an OFRMPC problem is solved to optimize the controller parameters utilized at the next sampling time. The control performance of the one-step ahead OFRMPC approach in [163] is better than that of the traditional off-line OFRMPC approaches based on look-up table schemes, but the computational burden is slightly heavier.However, it is required to satisfy the strict assumption that the computational time for solving the OFRMPC optimization at each sampling time should be less than one sampling interval.

3) Tube-Based OFRMPC:For the tube-based OFRMPC approaches in [52] and [53], the estimation error and control error are bounded in minimal RPI sets. The on-line quasi-minmax OFRMPC optimization in [52] is solved to optimize one free nominal control input and nominal state with time-varying terminal constraint set. Then, the nominal system is steered to the origin. The on-line min-max OFRMPC approach in [53] optimizes nominal feedback controller gain and time-varying terminal constraint set at each sampling time. The computational burdens of the OFRMPC approaches in [52] and [53] are lighter, since only nominal system stability with less decision variables and constraints is required in OFRMPC optimizations.

The tube-based OFRMPC approaches in [54] and [145] synthesize off-line optimizations to design look-up tables and online RMPC optimizations to stabilize nominal systems. For the on-line quasi-min-max OFRMPC optimizations in [54]and [145], nominal control inputs are optimized to ensure that nominal system states are convergent to the origin, where the scaled and searched terminal constraint sets are respectively considered in [54] and [145]. The LMI decision variables and LMI constraints for the on-line OFRMPC optimizations in[54] and [145] are less and not related to the number of submodels in LPV and T-S fuzzy systems, and thus the computational burden is lighter.

IX. FUTURE RESEARCH DIRECTIONS ON OFRMPC FOR LPV SySTEMS

The research fields on OFRMPC approaches for LPV systems have not yet reached a full maturity, and there is room for many possible developments and improvements. For the future developments of OFRMPC for LPV systems, the following future research directions are interesting.

A. Sampled-Data OFRMPC for Continuous-Time LPV Systems

In this survey, the documented results on OFRMPC for discrete-time LPV system models are mainly summarized and discussed, where the controlled continuous-time LPV systems are discretized into discrete-time LPV systems by choosing a fixed sampling period. However, discretization techniques often introduce errors and LPV system parameters are assumed to be constant between two successive sampling instants. The sampled-data control for continuous-time systems addresses the closed-loop robust stability and control performance by implementing the control inputs at the sampling instants such that the inter-sample dynamics between two successive sampling instants can be considered [165],[166]. Sampled-data state feedback RMPC approaches for linear systems in [167], nonlinear systems in [168], [169], and LPV systems in [170]–[172] have been studied. Sampled-data output feedback MPC for uncertain and nonlinear systems is also studied in [173]. To cope with constrained LPV system with unknown system states, it is more appropriate to further explore the sampled-data OFRMPC approaches for continuous-time LPV systems.

B. Stochastic OFRMPC for Probabilistic LPV Systems

Deterministic OFRMPC approaches often assume that LPV system parametric uncertainties, estimation errors, disturbances and/or noises are bounded within compact sets. Then,recursive feasibility and robust stability of formulated OFRMPC optimizations are usually achieved by explicitly resorting to the worst-case analysis, where all the possible realizations of bounded system uncertainties are often considered such that conservative constraints and control performance are provided. To overcome these limitations, stochastic MPC further considers the possible priori knowledge of distribution information for system uncertainties such that the violations of soft constraints can be treated within a given probability and better control performances in the statistical sense can be achieved [174], [175].

State feedback stochastic MPC approaches for LPV systems with stochastic scheduling parameters have been studied in [176] and [177]. In addition, for linear systems with additive stochastic disturbances, stochastic OFRMPC approaches that include state estimations are considered in [178]–[180].The stochastic OFRMPC schemes for LPV systems with additive stochastic disturbances should guarantee recursive feasibility and closed-loop stability with respect to probabilistic inputs and state constraints in the mean-square sense, where probabilistic invariant sets that include the state estimation for closed-loop systems are often required.

C. Anticipative OFRMPC Via Exploiting Scheduling Parameter

Most of the available OFRMPC approaches for LPV systems often consider two cases: i) the scheduling parameters of LPV systems are uncertain at each sampling time (e.g., the OFRMPC approaches in Sections II-B and II-D); ii) the scheduling parameter of LPV systems is exactly known at the current time, but the worst cases of the future scheduling parameters are considered (e.g., the OFRMPC approaches in Sections II-A, II-C, and II-E). For both cases, the formulated OFRMPC optimizations guarantee robust closed-loop stability and constraint satisfaction with respect to all the possible future realizations of scheduling parameters, and have not fully exploited the information on future scheduling parameters. In some cases, the variations of future behaviors in scheduling parameters are possibly available.

In anticipative RMPC approaches for LPV systems, the controllers can take advantage of the information on the trajectories of the future scheduling parameters of LPV systems such that the conservativeness in RMPC optimization can be reduced to improve control performances [181]. In recent years, there have been some state feedback anticipative RMPC schemes for LPV systems (e.g., [42]–[44], [182],[183]), where multi-step open-loop predictions are considered and the technique of robust tubes is exploited to deal with system uncertainties resulting from the uncertain future scheduling parameters of LPV systems. Compared with state feedback anticipative RMPC approaches, anticipative OFRMPC approaches for LPV systems can be deeply investigated to develop multi-step open-loop predictions for tube-based OFRMPC approaches, where time-varying state estimation error bounds resulting from uncertain future scheduling parameters should be further included in robust stability of OFRMPC optimizations.

D. Data-Driven OFRMPC for LPV Systems Via IO Data

Design of RMPC controllers with closed-loop stability and better control performance for LPV systems critically hinges on the identified accurate LPV state space models. However,obtaining accurate state space models is often the most timeconsuming and expensive procedure for controller design.Although state observer systems are not required in the OFRMPC scheme with the IO models in Section II-F, the IO models are state-space models. Data-driven MPC considers unknown system models and utilizes the Hankel matrices consisting of IO data to predict system future behaviors and design controllers. Hence, data-driven MPC can be inherently regarded as the direct output feedback MPC scheme since no state measurements and the transformation of state space models are required for its implementation.

Data-driven MPC is a promising alternative and often suitable for the scenarios where first principles models cannot be easily designed and/or system parameter identifications are too costly [184], [185]. Based on the extension of behavior theory and the assumption that sampled data sets satisfy the persistence of excitation condition, data-driven MPC approaches have been recently developed for linear systems in [186]and [187], and for LPV systems in [188]–[190]. However,data-driven MPC with guaranteed robust stability and recursive feasibility for uncertain systems is immature. Robust data-driven MPC approaches for LPV systems concerning IO formulation are a novel and promising investigation field in the future.

E. Adaptive OFRMPC With Uncertainty Identification

The reviewed OFRMPC optimizations assume that system uncertainties are often bounded within given constraint sets.However, the control performance is often conservative since it is difficult to accurately approximate the effects of system uncertainties when dynamic systems evolve over time. As an alternative promising solution, adaptive RMPC approaches can incorporate on-line system identification or parameter adaptation into RMPC optimizations to reduce conservativeness.

The problems of adaptive RMPC approaches for uncertain systems have received increasing attention in recent years. For linear systems, an adaptive RMPC approach with on-line updating unknown parameters and uncertain sets via the technique of recursive least square is proposed in [191], where less conservative control performance is achieved compared with the traditional robust tube-based state feedback RMPC methods. For linear and nonlinear systems with unknown parameters and additive bounded disturbances respectively in[192]–[194] and [195], adaptive RMPC approaches combine the techniques of robust tubes and set-membership identification to provide robustness with respect to uncertain parameters and disturbances. Most of adaptive RMPC approaches assume that system states are available. It is promising that recent results on OFRMPC approaches for LPV systems can combine with the developed adaptive RMPC schemes. Then,on-line system identifications and parameter adaptations can be integrated to deal with time-varying system uncertainties and reduce the conservativeness in OFRMPC optimizations for LPV systems.

X. CONCLUSION

This survey comprehensively summarizes various results on OFRMPC for LPV systems over the past two decades, and proposes possible classification criteria and the relationships among the large number of literatures on OFRMPC. The extensions of OFRMPC for LPV systems to other related uncertain systems such as T-S and IT2 T-S fuzzy systems are also discussed. For different kinds of OFRMPC optimizations,various methods of dealing with system uncertainties and the constraints on bounded disturbances and/or noises, the current system states, robust stability, control inputs, system states and outputs are given. The key issues (including nonconvex BMIs, estimation error constraints and bounds, recursive feasibility and robust stability, control performance, and on-line computational burden) on different OFRMPC optimizations are summarized. Finally, the future research directions on OFRMPC for LPV systems are suggested.drives: Advances and trends,”IEEE Trans. Industrial Electronics,vol. 64, no. 2, pp. 935–947, 2017.