Caputo型对流方程的间断伽辽金有限元方法
2022-10-26王震
王 震
(江苏大学 数学科学学院, 江苏 镇江 212013)
0 引言
分数阶微积分算子由于其特有的非局部性,能够对具有记忆或者遗传特性的材料和过程进行更为准确的描述和刻画,而受到了越来越多学者的关注[1-3]。但也正是这个特性使得分数阶微分方程的解析解很难求得,因此利用数值方法求解分数阶微分方程成为一个有重要意义的研究课题。考虑如下的时间分数阶对流方程:
x∈Ω=(a,b),t∈(0,T]
(1)
初始条件为:
u(x,0)=u0(x),x∈Ω
边界条件为:
u(a,t)=0,t∈(0,T]

0<α<1
初值u0(x)和源项f(x,t)是已知函数,T是给定的有限时间,Γ(·)是Gamma函数。容易看出,问题 (1) 是一个时间分数阶双曲型方程。为了数值计算的方便,假设:
u(b,t)=0,t∈(0,T]
到目前为止,关于整数阶对流方程数值方法的研究已经取得了很多成果[4],而这类方程在分数阶导数意义下的发展却很缓慢,直到近几年才有零星结果。Li等[5]考虑了3类方程(即分数阶对流扩散方程、分数阶对流占优扩散方程和分数阶对流占优分数阶扩散方程)的建模。随后,他们在文献[6]中建立了求解空间分数阶对流方程的有限差分方法。最近,Li和Wang[7-8]研究了一维和二维Caputo型分数阶对流方程的间断伽辽金(discontinuous Galerkin,DG)有限元方法。注意到时间分数阶偏微分方程的解在初始时刻可能会表现出一些弱正则性,为了保证格式在时间方向上的一致高精度,他们采用非均匀网格上的L1差分方法离散方程的时间分数阶导数,空间方向使用DG有限元方法近似,从而构造了全离散数值格式,并对格式的稳定性、收敛性和误差估计进行了详细讨论。从结果可以看出,文献[7-8]中构造的数值格式在时间方向上的精度最多只能达到2-α阶。
将继续研究解在初始时刻具有弱正则性的Caputo型对流方程 (1) 的有效数值解法,即假设问题(1)的解满足:
‖∂lu(x,t)/∂tl‖H2(Ω)≤Cu(1+tα-l),
l=0,1,2,3,t∈(0,T]
(2)
式中:Cu>0是一个与u的正则性有关的常数。首先使用非均匀网格上的Alikhanov公式离散Caputo时间分数阶导数,空间方向使用DG有限元方法逼近,进而给出全离散数值格式。然后对格式的稳定性、收敛性和误差估计进行严格的证明,并通过数值算例进一步验证理论分析的正确性和算法的有效性。结果表明,通过选取合适的分级网格参数,格式在时间方向的误差可以达到最优收敛阶2,比之前的2-α阶要高,空间方向是k+1阶收敛的,其中k是分段多项式的次数。
1 预备知识
本节将给出数值分析中一些常用的记号、定义和投影,并且假设C>0表示一个与时间步长和空间步长均无关的有界常数,不同处含义可能不同。首先,对于任意非负整数s,记Hs(Ω)为定义在区间Ω上的标准Sobolev空间,其范数为:
‖·‖s=‖·‖Hs(Ω)
令
函数u和v在区间Ω上的L2内积以及相应的L2范数定义如下:
N表示网格单元总数。单元中心和单元长度分别记为:
xi=(xi-1/2+xi+1/2)/2,hi=xi+1/2-xi-1/2
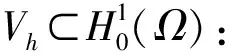
Vh={v∈L2(Ω)∶v|Ii∈Pk(Ii),i=1,2,…,N}
式中:k≥0,Pk(Ii)表示定义在网格单元Ii上的k次多项式函数空间。由于函数u在相邻的2个单元交界处会有左右逼近的2个值,因此定义:
记u在单元交界处的跳跃值为:
[|u|]i+1/2=u+|xi+1/2-u-|xi+1/2

(3)
式中:C>0是一个与空间步长h无关的常数,且:

2 主要结果
本节构造Caputo型对流方程(1)的全离散DG有限元格式,并分析格式的稳定性、收敛性和误差估计。对于给定的有限时间T和正整数M,记:
tn=T(n/M)r
式中:r≥1表示分级网格参数,n=0,1,2,…,M表示网格节点。将有限时间区间[0,T]划分为:
0=t0 非均匀时间步长τn=tn-tn-1,n=1,2,…,M。容易看出,当r=1时,网格是均匀剖分。为书写方便,引入如下记号: tn+σ=tn+στn+1,un+σ=u(x,tn+σ) un,σ=σun+1+(1-σ)un,n=0,1,…,M-1 为了对时间分数阶导数进行离散,需要介绍Caputo分数阶导数在非均匀网格上的Alikhanov逼近公式为[10]: (4) n≥1, 0≤j≤n-1 n≥1, 0≤j≤n-1 令 ▽tuj+1=uj+1-uj, 0≤j≤n, 0≤n≤M-1 对于n=0,1,…,M-1,有: 通过参阅文献[11],可以得到下面的不等式: (5) 式中:ωβ(t)=tβ-1/Γ(β),πA>0是一个常数。 方程(1)在t=tn+σ时刻的变分形式为:寻找u∈H1(Ω),使得: (6) 式中:v是空间H1(Ω)中任意的检测函数。 (7) (8) 本小节考虑全离散DG格式(7)的稳定性,首先介绍如下2个引理。 式中:{φn+1,ψn+1|0≤n≤M-1}是2个非负序列。 如果最大时间步长τM满足: τM≤(2πAΓ(2-α)Λ)-1/α 那么有如下不等式成立: 引理2[12]如果σ=1-α/2,那么对任意的函数u成立不等式: n=0,1,…,M-1 (9) 根据引理2和Cauchy-Schwarz不等式可得: 再利用引理1进一步得到: (10) 由式(5)可知: (11) 将式(11)代入到式(10)中,可得: 证明完毕。 本小节给出方程(1)的全离散DG格式的最优误差估计。下面先介绍2个非常重要的引理。 引理3[13]设σ=1-α/2,则对任意的函数u(t)∈C3(0,T],以下不等式成立: 0≤n≤M-1 式中: n=1,2,…,M-1 n=1,2,…,M-1 2≤i≤n≤M-1 此处I2,1u(s)表示在ts-1、ts和ts+1对u(s)的二次插值多项式。 引理4[13-14]如果u∈C[0,T]∩C3(0,T]且满足条件(2),那么有: u(x,t)∈L∞(0,T;Hk+1(Ω)) 最大时间步长τM满足: 令σ=1-α/2,则有如下估计: 式中:有界常数C>0不依赖于时间步长M和空间步长h。 证明令 (12) 由方程(6)和(7)可得误差方程: 若记 然后将式(12)代入上述误差方程可得: 再利用投影算子的定义进一步得到[15]: (13) 由引理2和Cauchy-Schwarz不等式可得: (14) 根据式(3),有下面的估计式成立: 此处用到了不等式: τn+1≤CTM-rnr-1,n=0,1,…,M-1 因此,有: 结合上式以及n=0的情形可得: (15) 进一步地,由引理3和引理4可以推出: (16) 将式(16)代入式(14),然后利用Cauchy-Schwarz不等式可得: 再根据式(5)以及引理1便可推出: Chk+1≤CM-min{rα,2}+Chk+1 最后利用插值性质(3)和三角不等式即可完成定理的证明。证明完毕。 本节通过一个数值例子来验证格式(7)的精度和有效性。 例1考虑下面的Caputo型对流方程: (x,t)∈(0,1)×(0,1] (17) 初始条件为: u(x,0)=0,x∈(0,1) 边界条件为: u(0,t)=0,t∈(0,1] 式中: 2π(tα+t3)cos(2πx) 精确解为u(x,t)=(tα+t3)sin(2πx)。 容易看出,方程(17)的精确解在初始时刻有一定的弱正则性,因此可以利用全离散格式 (7) 来求解上述方程。首先,验证格式在时间方向上的精度。选取N(N=1 000)足够大,使得空间方向的误差不影响时间方向的精度。表1和表2分别列出了当分级网格参数r取1和(3-α)/α时,在不同的分数阶导数α下的时间方向L2模误差和收敛阶,结果表明全离散DG格式(7)在时间方向的收敛阶为O(M-min{2-α,2}),这与定理2中的结果是一致的。如果选取r=(3-α)/α,那么格式在时间方向可以达到最优的收敛阶2。其次,验证格式在空间方向上的精度。固定时间方向的剖分为M=2 000,选取分级网格参数r=(3-α)/α,以k=1为例,从表3可以看出格式(7)在空间方向是k+1阶收敛的。 表1 当r=1,N=1 000,T=1时,格式(7)时间方向L2模误差及收敛阶 表2 当r=(3-α)/α,N=1 000,T=1时,格式(7)时间方向L2模误差及收敛阶 表3 当k=1,M=2 000,T=1时,格式(7)空间方向L2模误差及收敛阶 1) 构造了一个新的求解Caputo型时间分数阶对流方程的有限元逼近格式,此格式在时间方向上比已有算法的收敛精度高。 2) 证明了全离散数值格式的稳定性、收敛性和误差估计。通过数值算例检验了当前算法的有效性以及数值格式的收敛精度,为以后进一步研究高维情形归纳出一种基本的分析框架。 3) 所提出的数值算法主要适用于方程是线性的情形,将其推广到非线性方程并且证明格式的收敛性是一个难点。接下来将考虑构造合适的离散分数阶Gronwall不等式来克服这一困难。





2.1 稳定性分析






2.2 误差估计


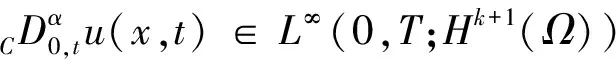


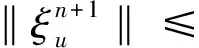
3 数值实验



4 结论
