五轴数控加工中心全域热特性评估方法

冉 靖，路世青，骆 辉，江 涛，张 红

(1.重庆理工大学 机械工程学院， 重庆 400054；2.长江大学 机械工程学院， 湖北 荆州 434023)

0 引言

五轴数控机床是发展现代生产力的必要设备,然而其多个发热源叠加导致机床热误差约占总误差的40%～70%[1-2]。采用硬件补偿方法会提高成本且此种方法补偿精度不太理想。因此,使用热误差软件补偿技术提高数控机床精度的方法是当今的热点和难点[3-7]。

数控机床热误差软件补偿技术的补偿能力取决于热误差模型的预测精度和稳健性[8]。目前国际科研人员在研究数控机床的热特性时，大多参考国际标准“机床试验规范-第3部分：热效应的测定(ISO230-3∶2020)”中的“五点法”进行主轴与工作台某一固定单点的热变形测量，并以此为基础，进行了机床热误差补偿精度及其稳健性的一系列研究，以提高机床的加工精度。Liu等[9]通过夹具将5个非接触式传感器固定在工作台上单一固定位置，测量主轴X、Y、Z的热误差变形量，结合岭回归算法在消除自变量在模型鲁棒性上的共线性和状态空间算法在描述系统内部结构和特征上的优势，提出了一种鲁棒状态空间模型(RSSM)，相比多元线性回归算法，其在此固定点的热误差预测精度提升了49%。Fu等[10]基于5个非接触式传感器在工作台固定位置测量主轴的X、Y、Z的热误差变形量，提出了一种基于k均值聚类和相关分析的温度敏感点选择方法，通过实验验证，此种温度敏感点选择方法可以提高热误差模型的预测性能和鲁棒性。Guo等[11]针对机床固定单点的热误差，提出了一种基于具有时空相关性的CNN-LSTM混合模型(ST-CLSTM)的静态热变形建模方法，具有良好的预测性能和较强的鲁棒性。Liu等[12]采用“五点法”测量工作台某一固定单点的热变形测量，提出了不确定性相关系数来选择温度敏感点的方法，提高了热误差模型的长期预测精度。Peng等[13]使用非接触式位移传感器测量五轴加工中心主轴轴向热误差，提出了一种考虑热弯曲效应的建模方法，此方法可以有效地预测轴向热误差和热弯曲角度。刘辉等[14]采用“五点测量法”测量工作台固定点热误差，提出了基于整体调整策略的神经网络建模算法，相比较于传统的BP神经网络，精度提升了50%。

然而，上述研究忽略了工作台不同位置存在热误差差异的情况，机床在实际加工过程中有的被加工件体积较大，在工作台上占有一定的空间位置而不是固定在工作台上某一位置。并且数控机床进行运动时，传动结构的复杂性会导致工作台的不同区域产生不同的热特性。因此，仅仅以固定单点测量作为机床热特性建模数据来源是存在较大隐患的。故需要对此进行深入研究，以获得真实有效的机床热特性检测方法和评估标准。

为了解决传统固定单点无法精确预测五轴数控加工中心全域热误差的原理性缺陷问题，本文提出了基于工作台热误差全域补偿模型的热特性评估方法。

1 热误差建模算法理论

1.1 温度敏感点选择

在热误差建立模型之前，模糊聚类算法和灰色关联度算法经常被作为温度敏感点挑选算法进行使用[15-16]。在保证所建模型精度的同时，降低过多温度变量带来共线性误差的影响。

1.1.1模糊聚类算法

模糊聚类算法是通过构造一个与研究变量属性相关的模糊矩阵，并根据一定的隶属度来确定聚类关系。假设域{xi|i=0,1,…,N}，其中xi是温度点。为了对X进行分类，需要计算分类对象之间统计关系的相关系数rij，然后确定模糊矩阵。通过传递闭包方法将模糊矩阵转化为等价矩阵，完成模糊分类。

设置xi∈U,xik(k=1,2…n)为xi的第k个测量值，相关系数如下：

(1)

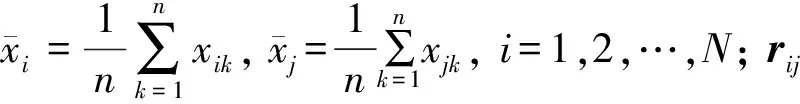
1.1.2灰色关联度算法

本文为了量化被分析变量之间的联系程度，采用灰色关联度算法来实现。灰色关联度计算值越大，变量之间的关联度就越大，反之越小。

计算公式为：

(2)

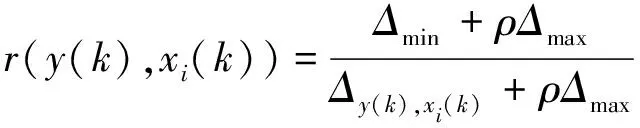
(3)

其中，y为因变量热误差，xi为因变量，即第i个温度传感器所测温度值，i=1,…,m，m为温度测点的总数。y(k)为所测热误差数据的第k个值，xi(k)为第i个温度传感器所测温度数据的第k个值，γ(y,xi)为热变形量和第i个温度测点之间的灰色关联度。ρ为系数，ρ∈[0,1]，一般取ρ=0.5。

Δy(k),xi(k)=|y(k)-xi(k)|为热误差数值与温度值差值的绝对量，形成如下绝对差值矩阵：(Δy(k),x1(k)…Δy(k),xi(k)…Δy(k),xm(k))。Δmin和Δmax为最小数和最大数。

1.2 多元线性回归(MLR)算法

在热误差应用中，多元线性回归算法[17]是建立多个温度测点与热变形量之间的关系式，其表达式为：

yi=b0+b1xi1+b2xi2+…+bkxik+ei

(i=1,2,…,n)

(4)

其中，xi1,xi2,…，xik为通过挑选的温度测点的增量值；b0,b1,…，bk为模型系数；yi为热误差模型的预测值；ei是预测值与实际测量值之间的差值。

1.3 全域建模算法

为了建立数控加工中心的全域模型，采用相同固定位置测点模型相互预测，所得到的预测热误差值通过最小二乘曲面拟合[18]求解出全域模型公式，然后在全域模型中带入工作台上各坐标点即可计算出工作台上各位置的热误差值，其公式为：

ft(x,y)=a0,t+a1,t+a2,ty+a3,tx2+

a4,txy+a5,ty2+a6,tx3+

a7,tx2y+a8,txy2+a9,ty3

(5)

其中，a0,t,…,a9,t为模型的系数；x与y为各测点的横、纵坐标；ft(x,y)为t时刻工作台上坐标为(x,y)处的热误差数据。

(6)

其中，M=(K,X,Y,X2,XY,Y3,X3,X2Y,XY2,Y3)；K=(1,…,1)T；N=(Δr1,t,…,Δr9,t)T；Δr1,t为第一个测点在t时刻的热误差值。

2 热误差测量实验

2.1 实验装置

为了获取数控加工中心工作台全域的热特性数据，本文以一台五轴数控加工中心KMC600SU为实验对象，设计了基于在线检测系统的热误差测量方法，用于机床的热误差数据采集。机床实物装置如图1所示。

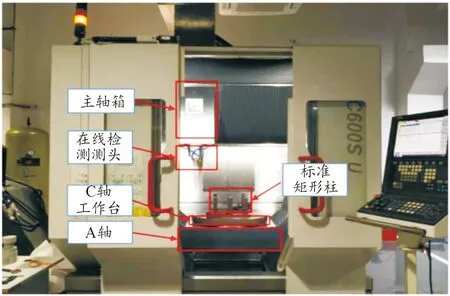
图1 实验对象

如图1所示为五轴数控加工中心KMC600SU的正面图像，包括了机床整体、主轴箱、主轴前端、在线检测系统、矩形检验柱及定位夹具等。

根据五轴数控加工中心工作台尺寸，提出采用在工作台上均匀分布9个标准矩形柱(后文用C1-C9表示)，矩形柱分布状况如图2所示，然后搭配在线检测系统测量机床的热误差的方案。其原理为：通过操作数控机床主轴以及工作台使在线检测触碰当前测点位置，并记录下此时机床的坐标，多次循环测量不同时刻的坐标点，通过对坐标点进行处理得到Z向偏差即为热变形量。

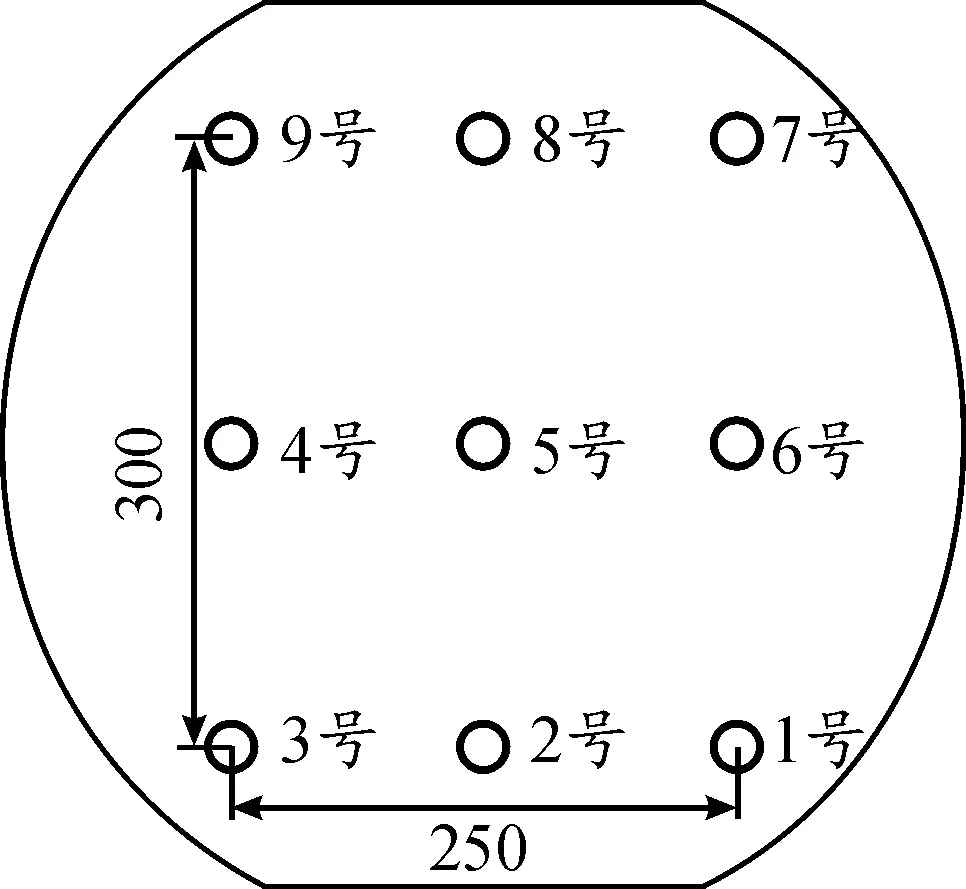
图2 各测点位置图

实验选择温度传感器DS18B20测量机床主要热源附近的特定点的温度数据，其温度测量范围为-55～125 ℃，最高分辨率为0.062 5 ℃，测量精度为±0.2 ℃。共使用10个温度传感器，后文用T1-T10表示，其具体安放位置如表1所示。

表1 传感器安放位置

2.2 实验方法

按照国际标准ISO 230-3∶2020标准对机床热误差的规定，本实验采用主轴空转方式运行。实验过程中，主轴以恒定4 000 r/min空转运行，X、Y轴以400 mm/min的恒定速度按照一定的轨迹进行水平运动。每运行6 min采集一次温度和热误差数据，机床运动时间为5 min，在线检测测量时间为1 min，每批次实验时间持续6 h以上。本文选取了在10月和11月跨度为2个月的4批次实验，本文中分别表示为K1-K4批次。

2.3 实验数据分析

通过对实验数据进行分析，可绘制出各实验批次的温升图像和各测点的热变形量图像。本文以K1批次实验为例，图3为10个温度测点的温升曲线。图4为工作台上9个测点的热误差变化曲线。

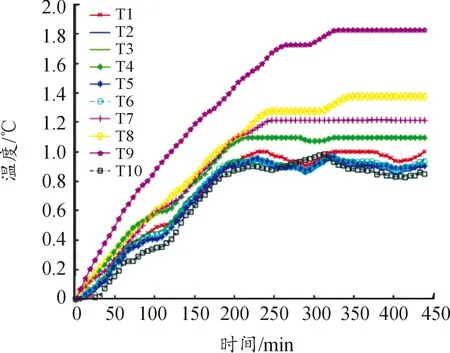
图3 K1批次T1-T10温升曲线

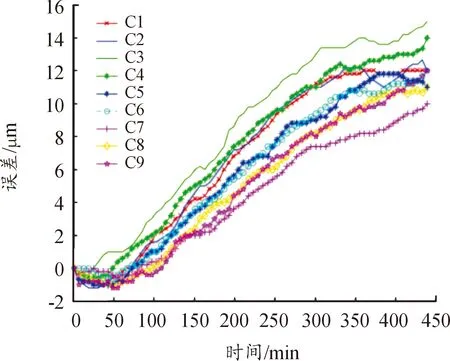
图4 K1批次各测点热误差曲线

从图4中可以看出数控加工中心工作台上各测点的热误差整体趋势为随着时间先上升后在机床热平衡后逐步趋于平稳，其中工作台上各位置测点随着温度升高的过程中热变形量存在差异，如在热误差变化过程中同时刻的C3与C7之间相差7 μm左右，同时为了更好地观察工作台各位置的变形量情况，画出在120 min、300 min的全工作台的热误差曲面图像，如图5所示。

图5 K1批次热误差曲面

可见，采用固定单点建模无法保证整个工作台的热误差预测精度，相比全域建模效果存在较大差异性。

3 热误差模型建立

3.1 固定单点模型

因工作台中心第五点的热变形量比较稳定，所以选取C5位置点建立固定单点模型[19]。采用多元线性回归算法建立模型时，首先对各实验批次的温度敏感点进行筛选，如表2所示。

表2 各实验批次采用模糊聚类结合灰色关联度选择温度敏感点结果

根据MLR算法原理，建立K1-K4批次的MLR模型，结果如表3所示。

表3 各实验批次固定测点的MLR模型

4.2 全域模型

本节以K1批次300 min时刻为例，结合1.2节多元线性回归算法得到工作台上各测点的热误差预测值，然后采用全域模型建模方法，得到K1批次的全域模型公式，结果如下：

f300(x,y)=0.627 8+0.002 9x-0.004 5y+

(0.530 7x2-0.400 0xy+

0.338 6y2+0.001 8x3-

0.003 2x2y+0.000 5xy2+

0.001 0y3)×10-4

(7)

其中，f300(x,y)为300 min时工作台上坐标为(x,y)处的热误差数据。

4 预测模型效果对比

根据K1-K4批次传统固定测点建立的MLR模型以及各批次的全域模型，分别对K1-K4批次进行预测精度分析。在热误差模型中，残差为模型预测热误差值与实际测量值之间的差值，其中残差值越小，表示模型的精度与稳健性越好。残差值计算公式如下：

(8)

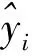
如图6所示为300 min时，采用全域模型和固定单点模型对K2实验批次的补偿效果。

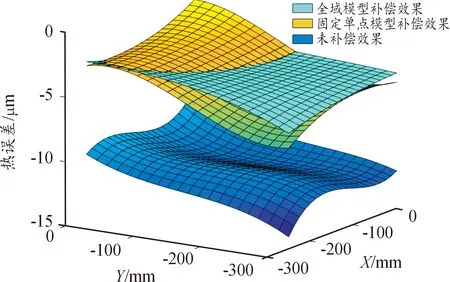
图6 K2实验批次第300 min补偿前后整个工作台在Z方向上的热误差曲面

从图6观察得出，通过全域模型补偿之后的K2实验批次300 min时整个工作台范围内的热误差大大降低，采用全域方法得到的工作台的热误差图像比固定单点模型更加稳定。因此，下文进一步讨论对多批次实验的建模预测效果。

通过计算，得到2种模型对不同实验批次的预测精度结果，然后将模型预测残差值使用正态分布函数[20]的方法处理，如图 7所示为传统固定单点模型与全域模型预测残差值的3σ区间的概率分布，图中黑色曲线为固定单点模型、红色曲线为全域模型，横坐标为误差/μm，纵坐标为密度。表4为2种模型的热误差预测残差值在3σ区间的范围，第1行表示传统固定单点模型残差分布的左极限为-14.695 6 μm、右极限为16.604 4 μm、总范围大小为31.3 μm。

由图7和表4可以看出，全域模型的预测残差范围为-13.587 8～14.812 2 μm，总范围大小为28.4 μm。固定单点所建立模型的预测残差范围为-14.695 6～16.604 4 μm，总范围大小为31.300 0 μm。全域模型范围要小于固定单点模型，即在相同概率内全域模型的预测效果要优于传统固定单点模型。从而验证了本文所提出的全域模型可以显著降低热误差差异对整个工作台补偿效果的影响，能更加有效地展现机床的实际性能。

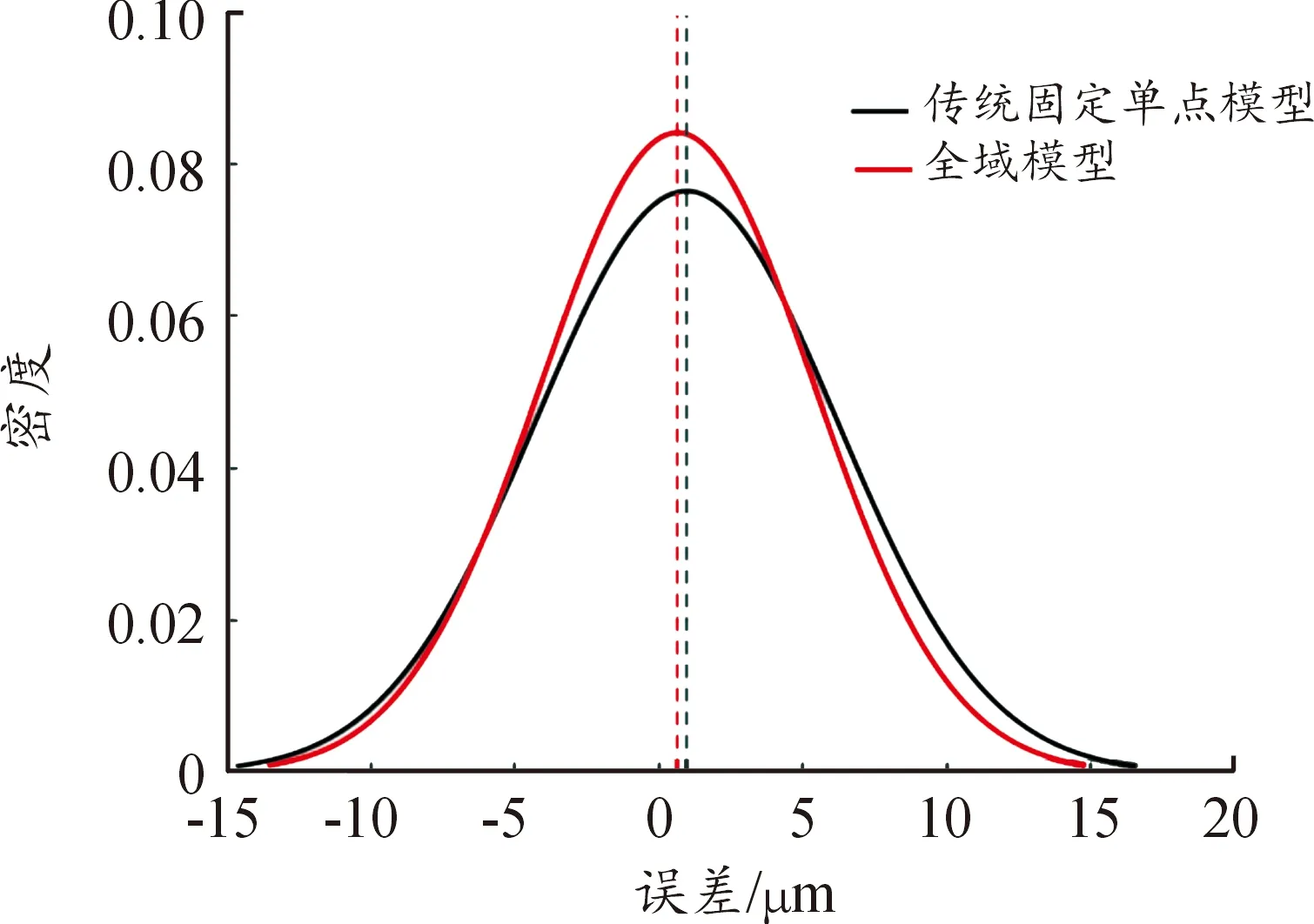
图7 固定单点模型与全域模型预测精度曲线

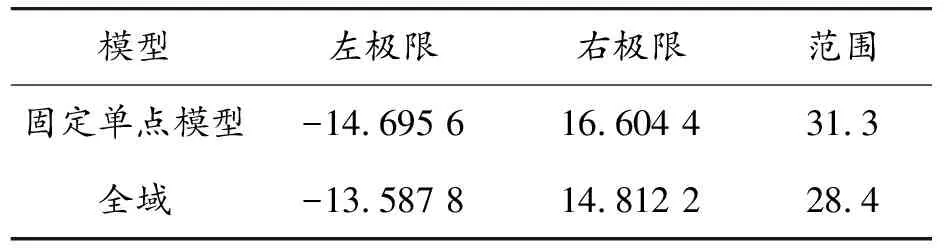
表4 固定单点模型与全域模型预测残差值的正态分布范围 μm

5 结论

本文为了研究五轴数控加工中心的全域热误差，搭建了基于在线检测系统的热误差实验装置。研究了五轴数控加工中心全域的热变形，发现在工作台不同位置产生的热误差具有差异性。

针对五轴数控加工中心全域热误差具有差异性，导致传统固定单点对整个工作台的补偿精度效果较低，提出了全域模型建模算法。实验分析证明，所提出的全域热误差模型在预测精度与稳健性上要优于传统固定单点模型。