辐条式非充气轮胎振动模态研究

2022-10-26邓耀骥朱明鑫王志越顾天乐仇李扬

重庆理工大学学报(自然科学) 2022年9期

邓耀骥,刘涛,朱明鑫,王志越,顾天乐,仇李扬

(1.扬州大学机械工程学院，江苏扬州 225127;2.四川轻化工大学机械工程学院，四川自贡 643002)

0 引言

轮胎在支撑整个车身的同时，还响应驾驶者对汽车行驶的动态命令，以此缓解路面不平对行驶汽车的冲击和各种复杂激励，提高汽车行驶的舒适性。传统轮胎，无论是斜交轮胎还是子午线轮胎皆存在易刺穿、爆损、爆胎、耐久性差以及不能满足特殊极端环境的使用等缺点[1]。

为了解决传统充气轮胎上述缺点，并进一步提高轮胎的行驶性能，近年来非充气轮胎的研发逐渐走向正轨，成为轮胎行业的重要研究方向[2-5]。非充气轮胎在轮胎材料的使用和结构的设计上与传统轮胎存在较大差异。非充气轮胎通常是由高分子材料制成的辐板或者网面，使它有着传统轮胎不具备的安全、可靠以及节能等优点。

非充气轮胎在国外的研发起步较早，产品迭代多，且外企及研发机构成果丰硕。目前，我国多家轮胎企业及研究团队也都在进行非充气轮胎的研发与设计，但是由于非充气轮胎起步晚，资金与技术有限，我国非充气轮胎基本上仍处于初期研发与设计阶段[6-10]。

轮胎是造成车厢内噪音和振动的主要因素。道路上的任何不平都会导致轮胎结构振动，进而导致车辆部件振动并产生噪音。因此，如何控制轮胎振动引起的共振及噪声问题是汽车行业的重点[11-13]。

本文首先介绍了非充气轮胎的设计准则以及振动模态理论，此后采用Abaqus软件对辐条式非充气轮胎进行有限元建模，对轮辐以及胎圈赋予聚氨酯和橡胶材料，在此基础上对辐条式非充气轮胎的固有频率及振型进行分析，研究支撑体辐板结构的个数以及支撑体辐板的厚度对非充气轮胎固有频率的影响；最后在相同变量的条件下对固定模态与自由模态的固定频率进行比较分析。

1 非充气轮胎设计准则与振动模态

1.1 辐条结构非充气轮胎的设计准则

非充气轮胎与充气轮胎的区别主要在于轮胎材料的选用和支撑体的结构设计两个方面。材料的选择上，非充气轮胎轮辐材料与充气轮胎轮幅材料有很大的不同。在非充气轮胎的使用中，轮辐的作用是吸收大部分轮胎受到的冲击载荷，是轮胎的主要受力部件，决定了非充气轮胎的性能。结构设计上，非充气轮胎一般由柔性的轮辐和超弹性的胎面两部分组成，其结构更加简单，性能更加优良。

本文研究对象为辐条型非充气轮胎，其主体为刚性轮毂、柔性轮辐和超弹性橡胶胎面。整个非充气轮胎是靠轮毂进行支撑，刚性轮毂可以避免非充气轮胎在使用中受到载荷冲击的影响而造成不稳定；柔性轮辐使用具有超弹性的橡胶材料，可以吸收来自路面的冲击载荷，以提升车辆的舒适性；橡胶胎面可以保证轮胎与地面良好的接触，也可以保证胎面具有良好的耐磨性，延长轮胎的使用寿命。

1.2 振动模态理论

模态分析法在工程领域的研究中是一种常用的方法，通常用于研究部件的结构动力特性。模态是指机械构件在运转中的固有振动特性，其每一阶模态中都有相对应的固有频率、阻尼比和模态振型。对这些每一阶模态相对应的固有频率、阻尼比和模态振型进行分析的过程就称之为模态分析。对模态进行计算，按计算方法的不同可以将模态分析分为计算模态分析和试验模态分析两种分析方法[14-15]。

四川省坡耕地水土流失综合治理试点工程建设实践探索………………………………… 周斌,江小华,孔祥东等（20.49）

模态特性有限元求解法首先将结构离散化，接着建立单元矩阵，从而得到结构整体的运动微分方程[14]：

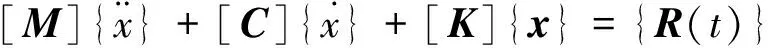
(1)

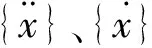
由有限元计算的方法取得模态就是获取上述微分方程的特征值，其每一阶次对应一个模态，每个阶次都有自己特定的频率、阻尼、模态参数。本文将对非充气轮胎的前10阶模态进行分析，得出其每一阶的频率以及振型，然后研究在单一变量下固有频率的变化情况。

2 非充气轮胎有限元建模

有限元分析法就是把需要求解的区域分解为许多小区域，这些小的区域在节点处相互连接。本文通过网格划分将辐条式非充气轮胎模型分解为许多的单元，轮胎在受到外加载荷时，其作用会分散到这些单元上，整体上分析这些单元受到的作用，以此得到仿真结果。这是真实系统理想化的数学抽象，可以将复杂的几何形状、复杂的材料特性和复杂的边界条件问题简单化。

2.1 非充气轮胎三维几何模型

为方便非充气轮胎基于有限元软件建立三维模型以及划分网格，采用单元构型法简化其过程。本文建立辐板式非充气轮胎三维几何模型，该模型主要由3大部分组成，包括胎面、支撑体辐板以及刚性轮毂，如图1所示。支撑体辐板厚度初始设置为3 mm，支撑体辐板的个数设置为36个。

图1 非充气轮胎几何模型示意图

2.2 材料属性设置

材料属性的定义是非充气轮胎有限元建模的重要组成部分，直接影响仿真结果的准确性。非充气轮胎的材料主要由橡胶和金属材料组成，其中橡胶材料属性通过单轴拉伸试验方法获得，金属材料属性通过查阅相关文献或由供货商提供。轮辐和胎圈采用橡胶材料。

Mooney-Rivlin模型由于能够较为准确地描述小、中变形的橡胶材料力学行为，而被广泛认可，其多项式形式的应变势能定义为：

(2)

式中：Ci, j为Rivlin系数；I1和I2为第一、第二应变不变量。

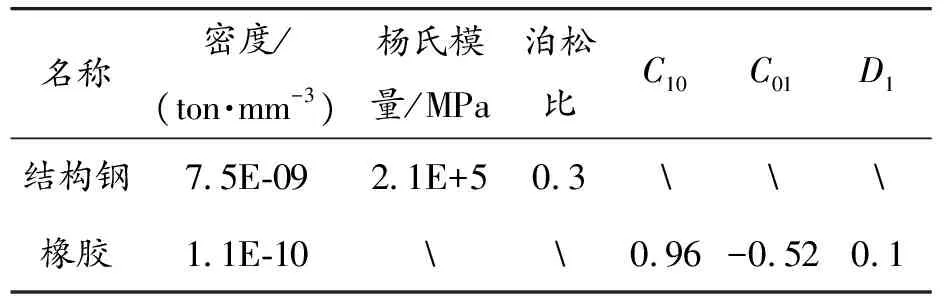
表1 所用模型材料的具体参数

2.3 网格单元类型的选择及划分

由于非充气轮胎模型采用整体建模方式，所以将模型划分为轮毂、辐板和胎圈3个规则部分，如图2所示。采用六面体网格对各区域进行划分，划分网格后的辐条式非充气轮胎模型如图3所示。

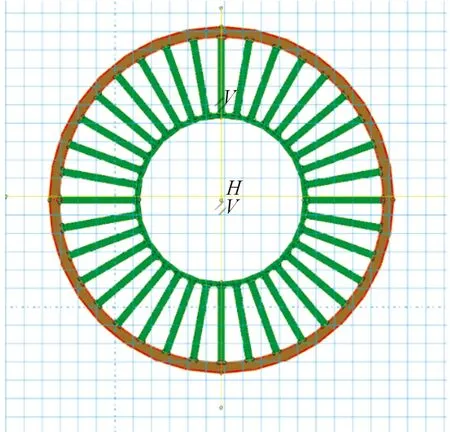
图2 非充气轮胎模型结构示意图

图3 辐条式非充气轮胎的网格划分示意图

2.4 边界条件及载荷设置

有限元分析中，胎面与路面的接触采用罚函数法描述。由于本文的非充气轮胎模型是整体建模的，块是通过草图划分出来的，所以不用考虑胎面区域与支撑体的接触问题以及支撑体与轮毂的接触问题。

根据作用力与反作用力大小相等、方向相反的原理，在模态分析时，一种方案为将轮毂固定进行固定模态分析，实施完全固定，限制6个自由度。另外一种方案为自由模态，即不对轮毂部分进行任何固定。

3 辐板式非充气轮胎振动特性分析

在轮胎的有限元分析中，通常进行实模态分析，计算中不考虑阻尼，计算结果提供了无阻尼的固有频率和振型。从非充气轮胎的模态分析中可以得到模态参数，该参数可以预测轮胎与路面或其他系统之间的相互作用，从而有效地防止轮胎产生共振和噪声，提升轮胎的使用性能。此外，利用模态分析所提供的各阶模态参数，联合结构响应求得外激励，从而实现载荷识别。

3.1 频率特征值与振型的表示

在工程领域中，获取解特征值的方法有直接求解法和向量迭代求解法。直接求解法适用于求解系统自由度较少的特征值和特征向量。向量迭代求解法包含有子空间迭代法、兰索斯迭代法等。采用向量迭代方法可以处理较大系统以求得该系统的少数特征值问题，运算时间则是根据该系统的自由度的数量和提取特征值数量而决定。

Abaqus软件中Lanczos求解器是软件默认的求解器。与其他求解器相比，Lanczos特征值求解器不仅可以确定求解的数目，而且可以确定最小的频率和最大的频段。在求解数量较低的模态阶数时，Lanczos求解器的计算精度较高，所以在求解器的选择上采用Lanczos求解器。考虑到高频振动对整车影响不大，提取并分析了辐条式非充气轮胎的前10阶振动模式，如表2所示。

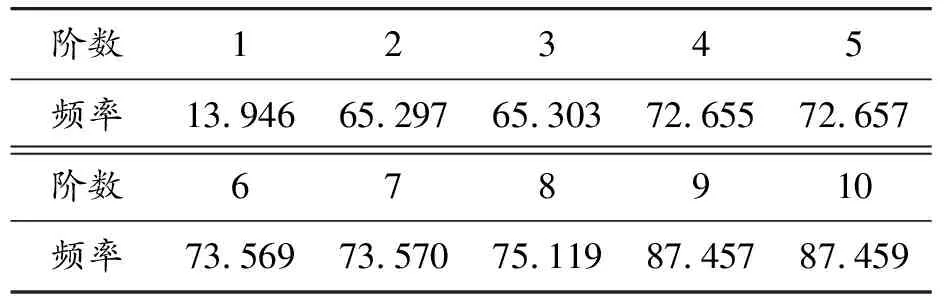
表2 辐板式非充气轮胎的前10阶频率 Hz

辐条式非充气轮胎固定模态的前8阶振型如图4所示。

图4 辐条式非充气轮胎固定模态的前8阶振型

由表2与图4可以看出，非充气轮胎的固有频率随着阶数的增加而增加，从第1阶的13.946 Hz增加到第10阶的87.459 Hz；同时非充气轮胎的变形越来越复杂，变形的部位主要是胎面与支撑体辐板，振动形式包括周向振型、径向振型和横向振型3类。

3.2 辐板式非充气轮胎固定频率影响因素分析

由于非充气轮胎的设计参数过多，如非充气轮胎的支撑体辐板单元的个数、支撑体辐板各单元的厚度、胎面厚度、带束层结构设计参数等都将可能会对非充气轮胎的固有频率产生影响，导致在研究时产生交叉复杂性。

支撑辐板作为非充气轮胎的主要支撑部件，其设计参数的选定对于整个辐板式非充气轮胎的性能具有重要意义。借此，采用单一变量的方法主要考虑关键参数，如辐板的数量以及辐板的厚度对非充气轮胎的固有频率产生的影响。

3.2.1支撑体辐板数量对固有频率的影响

将辐板式非充气轮胎的柔性支撑体辐板数量分别设置为12、24、36个，并建立对应的模型，提取了辐板式非充气轮胎前6阶的固有频率进行比较分析，如图5所示。

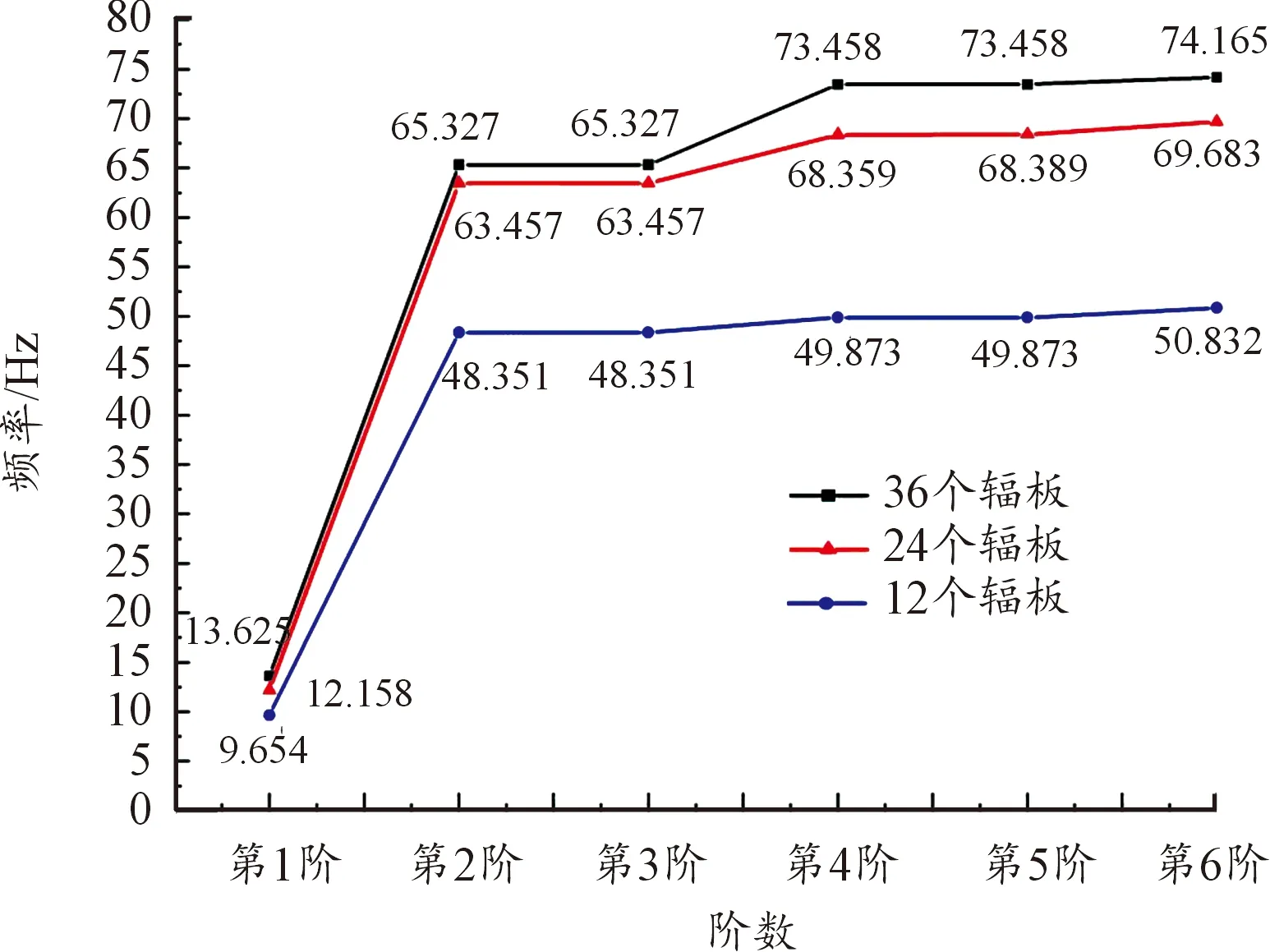
图5 不同支撑体辐板数量的非充气轮胎固有频率

从图5可以看出，不同支撑体辐板数量非充气轮胎的1阶固有频率的起始点都在10 Hz左右；随着阶次的增加，前2阶固有频率呈线性递增关系；由第3阶作为转折点，曲线缓慢递增，支撑辐板数量为36的非充气轮胎相比其他2种类型的频率数值变化规律较为明显；不同个数的支撑体辐板的每一阶固有频率随个数的增加而增加。这是因为随着辐板数量的增加，辐板式非充气轮胎的质量和刚度增加，导致固有频率增加。

辐板式非充气轮胎的支撑辐板数量的增加减小了轮胎在滚动过程中的滚动阻力以及自身的磨损，但同时过多的支撑辐板会将崎岖路面不平度以及路面坡度引起的外部激励导致车辆的操控性能和行驶平顺性降低，因此在设计个数时需要合理选择。

3.2.2支撑体辐板厚度对固有频率的影响

设置了3种不同的辐板厚度，分别为3、4、5 mm，辐板个数选取24个，进行仿真分析。不同辐板厚度的非充气轮胎前6阶固有频率如图6所示。

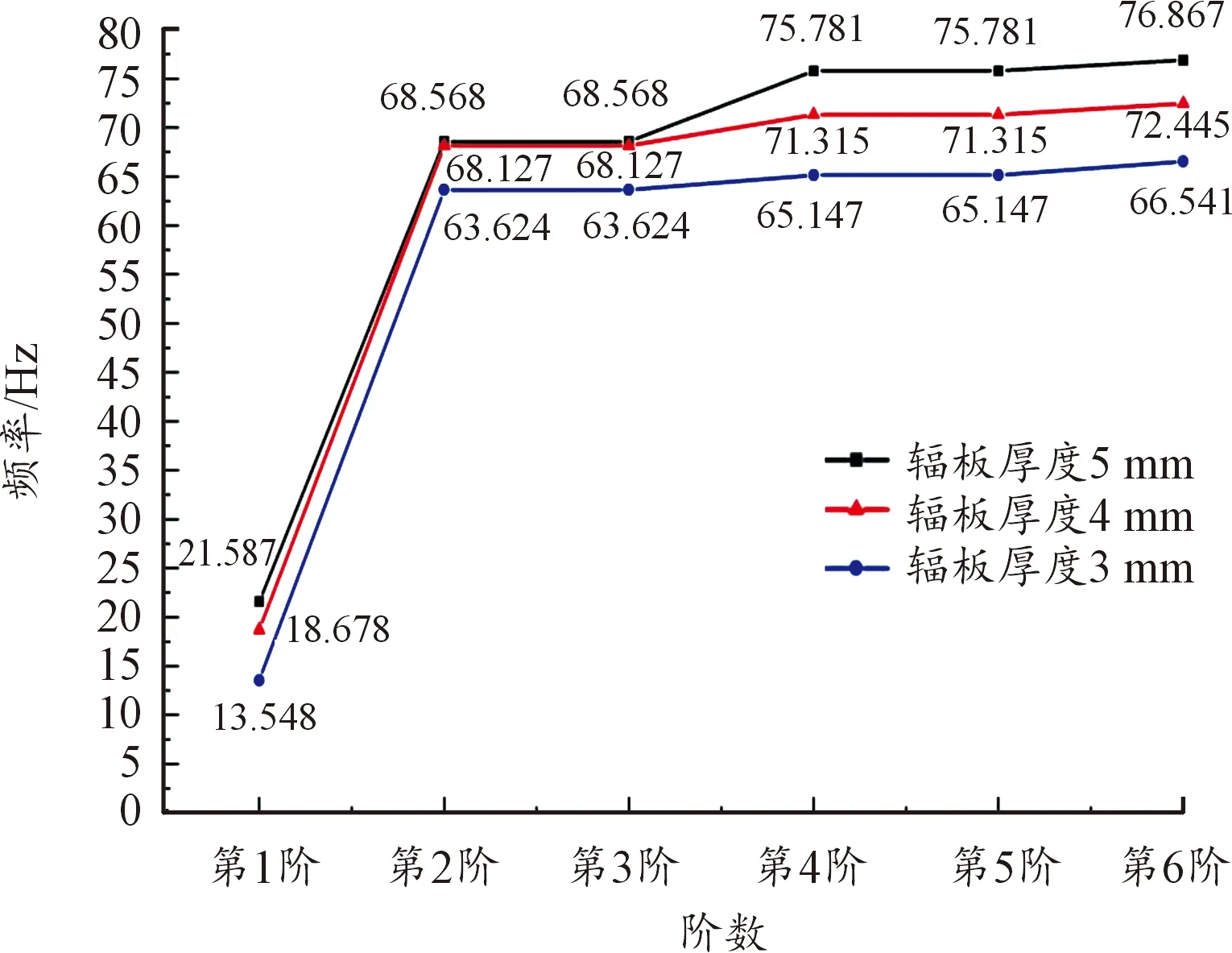
图6 不同辐板厚度的非充气轮胎固有频率

由图6可以看出：不同辐板厚度的非充气轮胎第1阶模态的固有频率都接近20 Hz，总体上都呈现出上升的趋势，且第1阶到第2阶变化最大，此后趋于平缓。支撑辐板个数为24，厚度为5 mm的辐板式非充气轮胎相比其他2种类型的频率数值变化规律较为明显，固有频率数值较高。这是因为随着辐板厚度的增加，辐板式非充气轮胎的刚度和质量增加，导致固有频率的增加。

3.3 固定模态与自由模态的频率对比

所谓自由模态分析，指对未有任何边界被限制的部件进行模态分析，此时部件在位移上没有受到任何约束。在自由模态分析时可能会得到固有频率为0的模态，这种模态称为刚体模态。一般情况下，自由模态在求解特征值得到的前6阶模态为刚体模态。除了刚体模态，其他各阶模态称作弹性模态。本节对比使用辐板个数为24，厚度为3 mm的非充气轮胎模型，其余因素保持不变。在自由模态中得到的前10阶频率如表3所示。

表3 自由模态下前10阶频率 Hz

由表3可以看出，在模型下第1阶固有频率与第2阶的固有频率为0，而且第2阶到第6阶的频率也非常接近0，所以可以认为在前6阶的模态为刚性模态。而刚体模态描述的是结构刚体移动，不存在弹性变形，所以其应力分布都为0。因为刚体模态不产生应力，所以可以忽略掉各阶刚体模态，仅对弹性模态进行模态分解，即取自由模态的后4阶与固定模态的后4阶进行比较。固定模态与自由模态第7阶—第10阶的频率如图7所示。