光诱渔船金属卤化物集鱼灯海面光场分布计算方法优化研究

王伟杰，万 荣, ，孔祥洪，肖俞辰

1. 上海海洋大学 海洋科学学院，上海 201306

2. 国家远洋渔业工程技术研究中心/大洋渔业资源可持续开发重点实验室，上海 201306

金属卤化物集鱼灯 (简称“金卤灯”) 是光诱渔业最常用的光源类型[1-6]。光诱渔船海面光场分布计算是集鱼灯应用研究的重要课题之一[3,7]。光场分布计算方法包括几何光学法[2,8-9]和蒙特卡罗(Monte Carlo, MC) 模拟方法[10-12]。几何光学方法中，Bae等[3]将点光源模型 (Point model, PM) 与指数衰减模型结合计算了渔船海面照度，假定灯具空间光场分布各向同性。Choi等[13]提出了线性光源模型 (Line model, LM) 计算灯光船周围海面照度，因其假定灯组为连续发光体，计算值大于实际情况。肖启华和张丽蕊[14]提出了面光源模型，适用于灯具表面积大、计算点与灯具之间小的光场数值的计算。Lai等[15]应用球面模型对LED集鱼灯进行二次透镜设计，并计算船舷两侧的海面光场分布。钱卫国和王飞[9]、叶超[16]、侍炯等[17]提出了配光曲线模型 (Light distribution curve model, LDC)并做了大量的海上实证研究。由于几何方法主要采用光在水汽界面的折射定律和在空气中直线传播规律，无法求解海面波动状态下的照度分布，学者开始引入蒙特卡罗方法求解光学传输问题[12,18-22]。张涤[12]应用蒙特卡罗方法研究了可见光水下信道问题，指出了不同波长光子信道衰减情况。官文江等[20]结合风浪斜率概率模型[23-24]，进一步应用蒙特卡罗提出了集鱼灯光场分布的计算框架。然而计算框架中的光子数取值问题和光子辐射模型还有待进一步完善，这两个环节决定了集鱼灯光场计算的准确度，进而影响到光场有效诱集范围、渔船之间合理作业间距等方面的估算。因此本文通过数值模拟方法讨论不同光子数取值对模拟结果稳定性的影响，同时根据灯具光度分布提出了新的灯具辐射模型并验证，结合新的辐射模型给出算例，为光诱渔船光场分布计算提供借鉴和参考。

1 材料与方法

1.1 坐标系

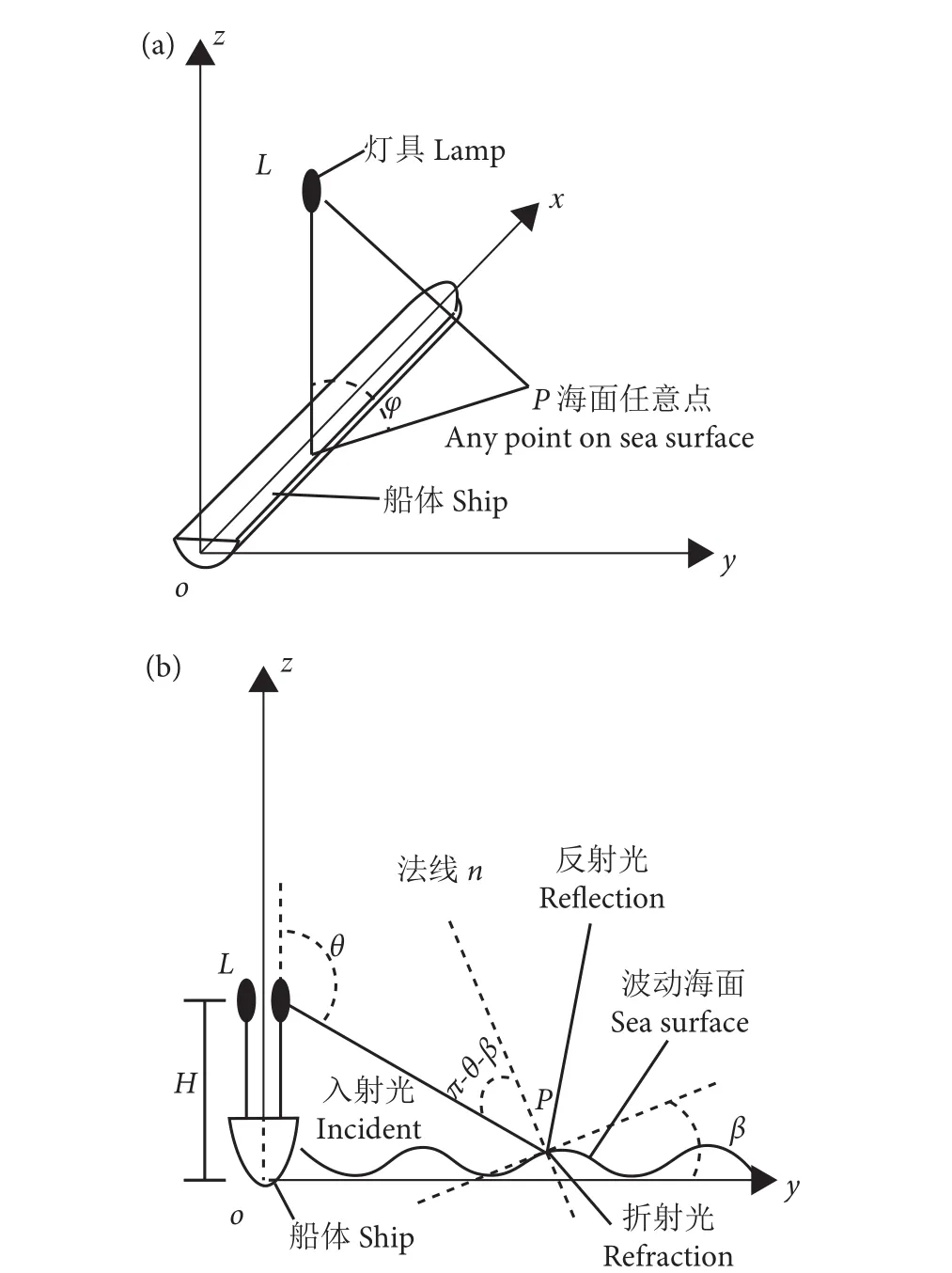
图1 灯具与计算点的相对位置及灯具安装示意Fig. 1 Relative position between lamp and calculation point and installation diagram of lamp

1.2 材料

选取目前光诱渔业中广泛应用的金属卤化物集鱼灯 (2 kW DCJ 2000TT型) 作为研究对象，选取目前光诱渔业中广泛应用的金属卤化物集鱼灯(2 kW DCJ 2000TT 型) 作为研究对象，集鱼灯额定功率2000 W，电压范围210～250 V，额定光通量220000 lm，灯头型号E39/79-A，灯具中心高度295 mm，全长465 mm，最大直径90 mm。

灯具光度分布数据在国家远洋渔业工程技术研究中心进行了测试，灯具配光在垂直方向和水平方向的配光曲线分布见图2。测试设备：远方光电GO-2 000光度分布测试仪，测试模式选系统内置的C-γ。

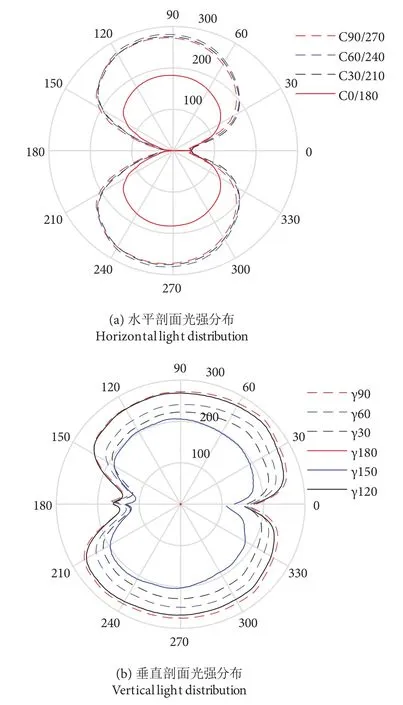
图2 灯具配光曲线Fig. 2 Light distribution curve

可以看出光强在水平和垂直剖面内的光强分布曲线存在一定差异，取C90/270和γ90平面内光强分布曲线，借助Matlab (R2015b) 软件用Fourier级数拟合灯具光强分布曲线，公式分别对应如下：

1.3 模型建立

蒙特卡罗方法是研究光辐射传输特性的经典方法[24-26]，通过将光束能量离散成大量光子，利用随机抽样方法追踪光子路径来解决光束传输问题，计算流程参考官文江等[20]的方法。模型计算假定条件：1) 模拟中所有光子无波长差异；2) 光子在水气界面只考虑反射与入射，无其他形式衰减；3) 不考虑光子在空气中的吸收与散射作用。

1.3.1 光子辐射优化模型

官文江等[20]报道的光子辐射模型中投影旋转角 () 使用均匀随机数生成，难以全面反映灯具辐射特征 (图1-a)。对此本文进一步优化，辐射模型考虑光子辐射天底角 () 和投影旋转角 () 两个方向的特征，计算公式：

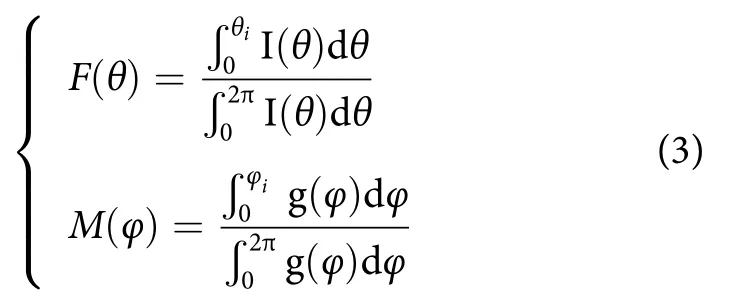
1.3.2 海浪斜率计算

光子从灯具出射后，沿直线投射至水面。而海面受风的影响形成了毛细海浪，因此交互界面有一定的斜率。根据Cox和Munk[27]观测，不同风速下的波浪面倾斜角经验概率密度公式：

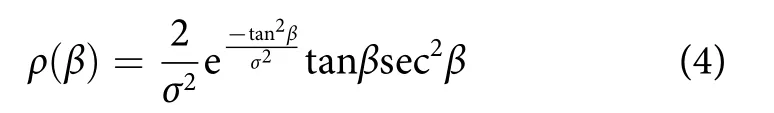
其中：σ2=0.003+0.005 12V，V为距海面10 m处的风速(m·s-1)；为波浪面与水平面的夹角，同样利用反函数法产生伪随机数[25]确定波浪斜率。

1.3.3 海面反射系数

光束经过大气-海水界面发生折射和反射，总反射率Rt计算公式：

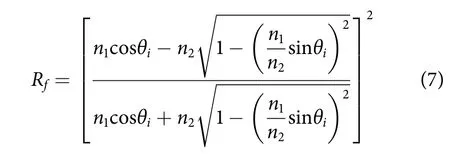
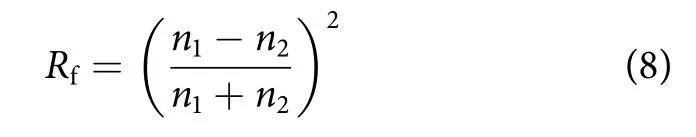
模拟过程中，依据轮盘赌法[26]进行判别：取随机数(为0～1内均匀分布随机数)，当，则光子落入水中，否则反射不予统计。对接收面进行栅格化处理后，通过统计每个栅格内的光子数能量与栅格面积之比得到照度值。

1.4 模型验证

为验证模型准确性，在光学实验室内完成验证测试。将灯具安装在自动旋转台上，灯高1.6 m，功率2 kW，照度计型号Hobo Mx2202，分辨率为0.01 lx。灯具安装在旋转平台上，照度计放置于地面，与灯具中心水平距离1～5 m，间隔1 m放置一个照度计，见图3-a中的t1—t5位置。测试过程中，转台绕C轴转动，从而测得灯具不同投影旋转角所对应的地面照度值，实际测试灯具与照度计布置见图3-b。

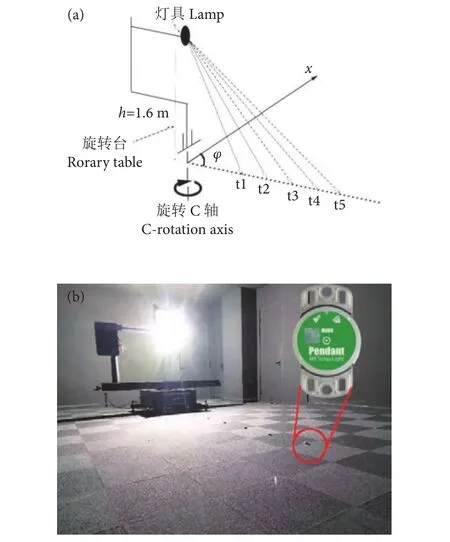
图3 验证测试方案Fig. 3 Verifying test

2 结果

2.1 光子数取值对模拟结果的影响

通过设定不同的光子数值105～1010讨论模拟结果的稳定性，重复模拟1 000次，取模拟结果的差异系数 (Coefficient of variation, CV) 作为稳定性计量指标，差异系数越低稳定性越高。结果显示：1) 对同一计算点，光子数从105增至1010，模拟结果差异系数减少；以与灯具水平距离5 m的计算点为例，当光子数增至108，差异系数为0.07%，光子数取值增大，差异系数减少至0.05%； 2) 相同光子数取值条件下，距灯具水平距离越近的计算点，计算结果稳定性越高；随着光子数取值增大，稳定性差异缩小 (图4)。

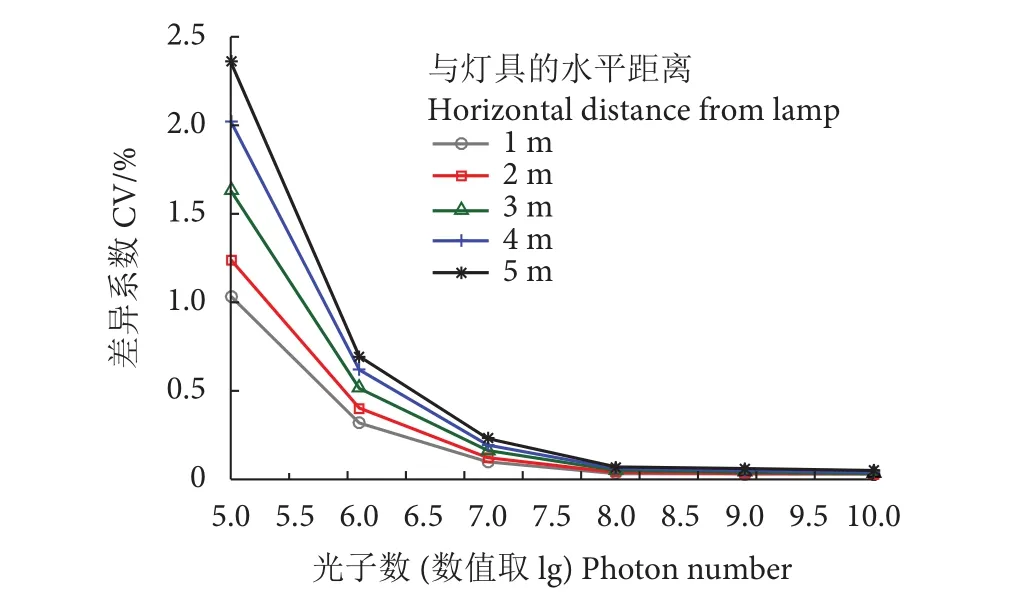
图4 光子数取值对模拟结果波动性的影响Fig. 4 Effect of photon number on volatility of modeling results

2.2 光子辐射模型优化

金属卤化物灯由于内部支架等遮挡影响，其空间光场分布在水平切面内并非饶轴对称 (图2-a)。针对新的光子辐射模型不同出射方向 (=90°、60°、30°、0°) 的照度值进行计算并实测，结果显示新模型计算结果与实测相对误差分别为5.12%、4.72%、3.28%、5.03%，平均值为4.53%，未优化模型相对误差均值为5.23% (图5)。不同方向上的计算结果差异系数小于0.08%，模拟稳定性较好 (图6)。

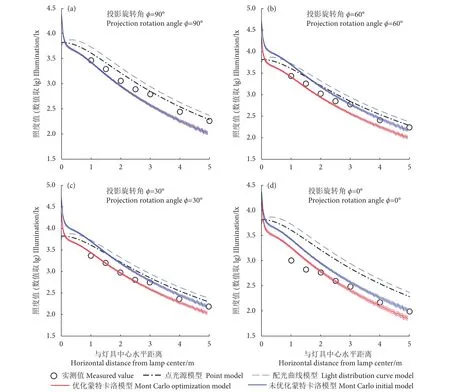
图5 优化模型不同出射方向计算与实测比较Fig. 5 Comparison of different light field calculation models

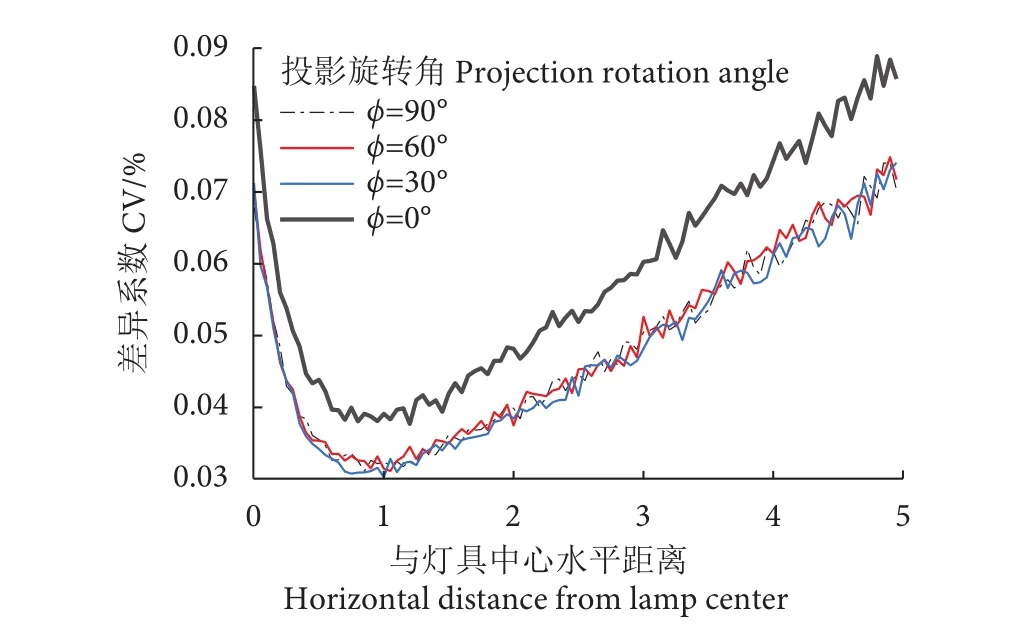
图6 优化模型不同出射方向计算的差异系数(光子数取值为108)Fig. 6 Coefficient of variation of optimized model simulation results (Photons number of 108)

作为对比，基于点光源模型的模拟结果与实际的误差分别为3.57%、4.57%、6.81%、17.1%，平均值8.41%，显然误差增大；基于配光曲线模型计算结果与实际的误差分别为7.07%、8.1%、10.42%、21.04%，平均值11.65%，误差最大。由上可知，本文提出的优化光子输出模型，能够较好地反映灯具光场的空间分布情况。

2.3 优化模型应用实例

结合本文提出的光子辐射优化模型，提供了光诱渔船在实际作业海域的光场分布算例，光诱渔船集鱼灯配置等参数见表1。风速取2 m·s-1，数据来自Noaa Erddap。实测值参照Choi等[13]的研究。

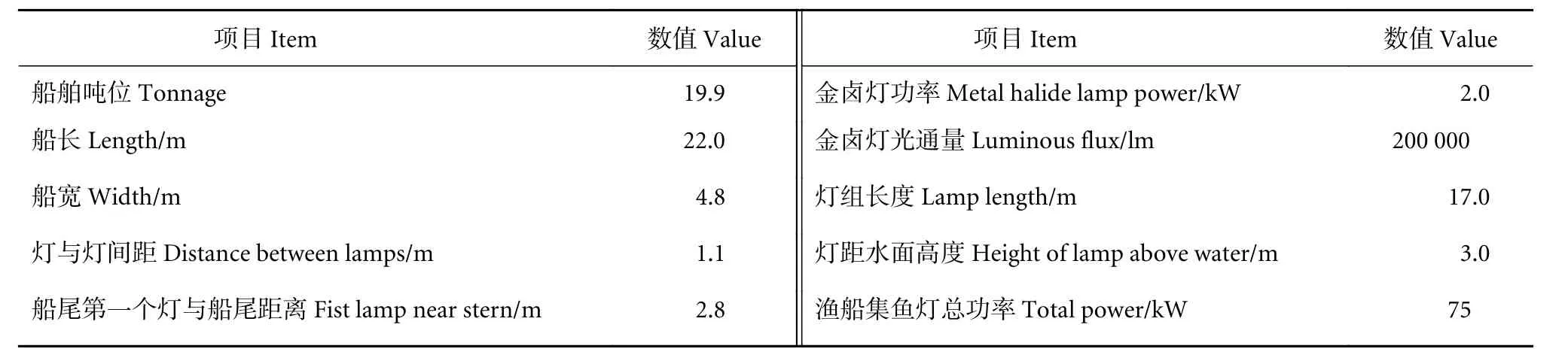
表1 模型参数表Table 1 Model parameters

根据上述参数计算了船舷一侧垂直于船舯线不同距离的照度值，并与Choi等[13]的实测值进行对比，结果显示优化后的蒙特卡罗计算结果与实测值平均误差约为5.23%，计算值接近实测值 (图7)。作为对比，应用线光源法和点光源法计算结果与历史研究实测值的平均相对误差分别为52.62%和54.00%，并且随着距离增大，相对误差增加。

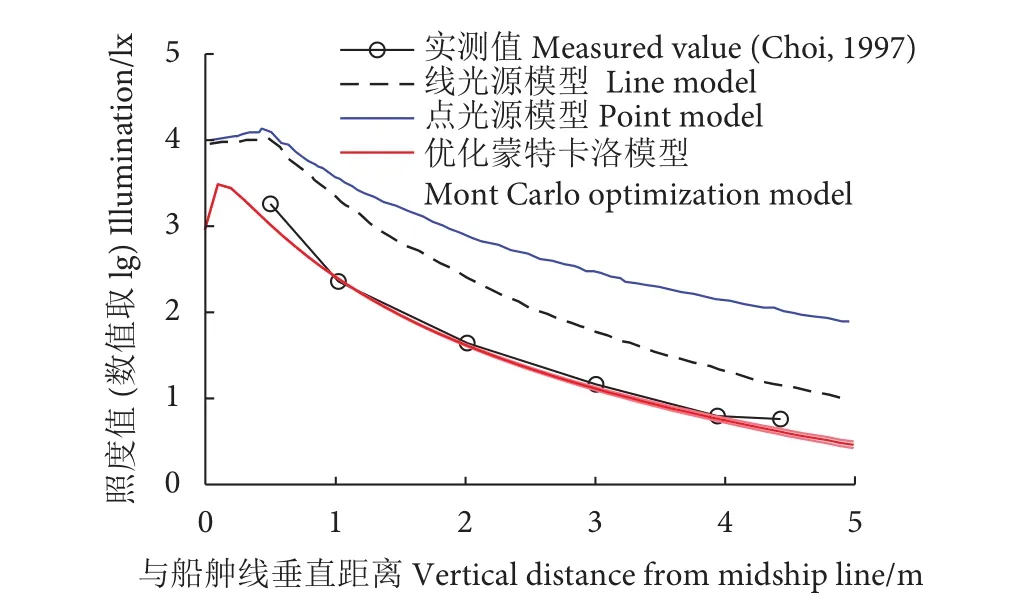
图7 优化模型应用计算结果与实测值对比(差异系数0～0.23%)Fig. 7 Calculated and measured values of horizontal illuminance at specific points beneath water(Difference coefficient 0-0.23%)

3 讨论

蒙特卡罗模拟通过大量随机抽样观察规律，样本量决定模拟结果的准确性。研究发现，光子数取值越大，模拟结果的差异系数越小且趋于极值。究其原因，当光子数取值足够大时，计算机所生成的伪随机数分布情况越接近概率分布函数，当然这还取决于伪随机数的生成方法[25,29]。本文通过预试验发现当光子数取值108时，模拟结果的差异系数为0.07%，此后差异系数趋于稳定值。本试验也发现光子数取值对模拟时长有较大影响。因此光束取值须兼顾模拟结果的稳定性、计算机性能等因素。本试验还发现，距离灯具越近的计算点，模拟的稳定性越高，这种现象在光子数取值较小时尤为明显，当光子数取值增大，远近距离计算点之间结果稳定性的差异减少。这是由于近光源处接受面所对应的灯具立体角较大，相同光子密度条件下，往往造成近光源处接受面能接受到更多光子，光子数越多，进一步造成计算结果越容易趋于稳定值。

针对光子辐射模型方面，本文利用灯具光度分布数据，从水平和垂直两个方向构建光子辐射概率模型并进行验证，发现优化模型的计算结果更接近事实。较官文江等[20]的研究，优化辐射模型充分考虑了灯具不同投影旋转角的光束辐射差异性，可以更加准确地计算灯与灯间光照叠加区域的亮度，进而计算合适的灯间安装距离以达到光源利用最大化。本文提出的光子辐射模型存在局限性，即假定不同的水平和垂直剖面内配光曲线分布趋势一致。因此，本文提出的建模方法无法应用于结构复杂的光源，建议选用二维随机变量分布函数描述[30]。

在算例中，本研究对比分析了几何算法与蒙特卡罗算法结果，发现线光源模型与点光源模型计算结果大于蒙特卡罗算法结果。原因是当海面具有一定斜率，光束在水汽交互界面的透射率发生改变。本文引用Cox和Munk[27]观测模型计算海面倾斜角，可拓展计算不同风速条件下的海面照度情况。

4 结论

本文利用数值模拟方法研究了蒙特卡罗模拟过程中光子数取值对计算结果稳定性的影响，讨论了造成这一影响的原因。同时，根据光度分布数据提出了光子辐射优化模型并进行验证，发现新的光子辐射模型与实际情况较为接近，能够较为全面地表征灯具不同方向光子的辐射特征。在此基础上，结合实际渔船的灯光配置参数和风速，计算了光诱渔船实际作业环境下的光场分布，结果显示在海面波动条件下，蒙特卡罗计算结果比几何方法计算结果更接近实测值。