函数对称性问题的解题策略

黄启贤 蔡海涛 张桂腾

(1.福建省莆田第十中学，351100；2.福建省莆田第二中学，351131)

以函数的对称性为切入点，考查函数的解析式、值域、单调性、周期性，常以客观题的形式出现，这是近年高考及各地质检题的热点问题.本文以2022年福建省质检数学第8题为例，探究函数对称性问题的解题策略.

(A)y=x-4 (B)y=x

(C)y=-2x+2 (D)y=-2x+6

该题以函数奇偶性为背景，结合函数部分区间解析式的已知条件,考查函数的奇偶性、曲线的切线等基础知识，考查推理论证、运算求解等能力，考查函数与方程、数形结合、化归与转化等数学思想和数学运算、逻辑推理等核心素养，体现基础性、综合性.本题基本思路为确定函数的对称中心,再利用图象对称的特性解题.解题过程应注意不同定义区间函数解析式的关系，可从数和形不同视角解决问题,体现解法的多样性.

一、解法探究

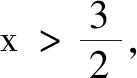
点评此解法是从奇函数具有中心对称的几何特征入手，先求函数的对称中心(1,1).根据切线也关于点(1,1)对称的特征，求出曲线y=f(x)在x=0处的切线方程，再求曲线y=f(x)在x=2处的切线方程，难点是判断函数y=f(x+1)-1的对称中心以及切线也关于点(1,1)对称的特征.

点评此解法是从求动点轨迹方程的角度入手，先判断出函数的对称中心是点(1,1)，再设点求轨迹方程.难点是判断函数y=f(x+1)-1的对称中心以及用求动点轨迹方程的方法求解析式.

二、解法归纳

1.结构特征

根据试题条件的结构特征,对函数性质的几何特征和代数表达进行有效转换.常见函数图象关于点对称或轴对称的试题条件等价转化如下.

(1)中心对称

y=f(x)的图象关于原点对称⟺y=f(x)是奇函数⟺f(-x)=-f(x)⟺f(-x)+f(x)=0.

y=f(x)的图象关于点(a,0)对称⟺y=f(x+a)是奇函数⟺f(-x+a)=-f(x+a)⟺f(-x+a)+f(x+a)=0.

y=f(x)的图象关于点(a,b)对称⟺y=f(x+a)-b是奇函数⟺f(-x+a)-b=-[f(x+a)-b]⟺f(-x+a)+f(x+a)=2b.

(2)轴对称

y=f(x)的图象关于y轴对称⟺y=f(x)是偶函数⟺f(-x)=f(x)⟺f(-x)-f(x)=0.

y=f(x)的图象关于x=a对称⟺y=f(x-a)是偶函数⟺f(-x+a)=f(x+a)⟺f(-x+a)-f(x+a)=0.

(3)点对称与轴对称组合

y=f(x)既关于x=a对称又关于x=b对称⟹y=f(x)是周期为T=2|a-b|的函数.

y=f(x)既关于(a,0)对称又关于(b,0)对称⟹y=f(x)是周期为T=2|a-b|的函数.

y=f(x)既关于(a,0)对称又关于x=b对称⟹y=f(x)是周期为T=4|a-b|的函数.

2.选择解题方向

可从代数角度和几何角度解题.代数角度常见有赋值法、求局部区间解析式等，进而解题;几何角度常用数形结合从几何上的中心对称或轴对称来解题.

3.灵活使用赋值法

控制含x项的符号变化和常数的大小变化，以此确定转化方向，这是通过代数运算解决问题的关键.

三、变式拓展

变式1(2022年厦门市第二次质检第10题)(多选)定义在R上的奇函数f(x)满足f(x+2)=-f(x)且当x∈(0,1]时，f(x)=1-x，则( )

(A)f(x)是周期函数

(B)f(x)在(-1,1)上单调递减

(C)f(x)的图象关于x=3对称

(D)f(x)的图象关于点(2,0)对称

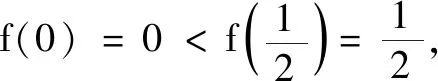
变式2(2022年福州市3月质检第11题)(多选)设函数f(x)的定义域为R，f(x-1)为奇函数，f(x+1)为偶函数，当x∈(-1,1]时，f(x)=-x2+1，则下列结论正确的是( )

(B)f(x+7)为奇函数

(C)f(x)在(6,8)上为减函数

(D)方程f(x)+lgx=0仅有6个实数解

综上，符合题目要求的选项为ABD.