轨道交通列车追踪运行模型及追踪间隔研究

张 海，倪少权，陈 韬，邹葱聪

(1. 西南交通大学交通运输与物流学院，四川 成都 610031； 2. 西南交通大学综合交通运输智能化国家地方联合工程实验室，四川 成都 610031； 3. 西南交通大学综合交通大数据应用技术国家工程实验室，四川 成都 610031)

1 引言

为满足我国城市轨道交通不断增大的客流需求，需实时调整列车运行计划，加大行车密度。列车追踪间隔是线路通过能力的重要指标及制定列车运行计划的基础。对列车追踪间隔进行精细化研究，是调整列车运行计划、提高线路通过能力的关键。

对城市轨道交通列车追踪间隔的研究主要是利用图解法、解析法及计算机仿真法这三种方法。闫丽霞等分析了绝对追踪模式及相对追踪模式下的列车追踪间隔，仿真结果表明：在相对追踪模式下可进一步缩短列车追踪间隔。王高磊等研究了基于压缩运行图冗余时间及加密列车运行线的区段通过能力计算方法。辛亚江阐述了移动闭塞工作原理，用相对运动观点建立了移动闭塞模式下列车区间追踪运行模型。李伟等基于移动闭塞特点及IEEE802.11无线通信协议，提出通信延迟情况下CBTC列车追踪间隔求解方法。梁宇等以成都地铁4号线为例，验证了可通过优化紧急制动距离、优化停站时间、优化列车紧急制动率以缩短正线列车追踪间隔。魏玉光等将列车在车站的停站作业虚拟为列车在闭塞分区运行，提出了城市轨道交通移动闭塞制式下列车追踪间隔计算方法。郑维耀等提出列车追踪动态间隔时间指标，在保证列车运行安全的前提下，通过适当减少图定列车追踪间隔时间以提高列车运行效率。郑艺等提出基于车车通信的CBTC列车区间追踪间隔模型，仿真结果表明该模型能有效缩短列车追踪间隔时间。Hansen将不同的列车追踪间隔计算方法应用于德国斯图加特铁路重组工程项目，并对各种方法进行了模拟验证。Armstrong等模拟了列车追踪运行场景，研究了在保障可靠性前提下提高车站通过能力的方法。

既有研究采用静态的、粗略的经验公式或简约的理论推导描述追踪间隔与其影响因素之间的关系。城市轨道交通CBTC列车追踪间隔受线路条件、列车性能参数、信号系统性能及元件布置等多种因素的影响，利用经验公式或者简约的理论推导不能准确反应列车实际运行情况，得出的追踪间隔和列车实际追踪运行有一定的偏差。本文针对既有研究的不足，充分考虑CBTC列车实际追踪运行情况及须满足的各种约束条件，基于列车追踪运行规律建立高精度的CBTC列车追踪运行模型，并设计高效的快速迭代算法对模型进行求解，将追踪间隔求解精度由1s精确到0.01s，保证了所得结果及结论的准确性，为城市轨道交通列车运营组织优化及精细化管理提供理论依据。

2 列车追踪运行场景

图1为某城市轨道交通线路配置图，该图展示了三站两区间轨道交通线路。列车从车站1下行站台发车点A发出，经过区间驶入车站2下行站台停车点G，停站时间结束后从G点发车，经过区间驶入车站3下行站台停车点M，停站时间结束后从M点发车，驶离车站3。

图1 轨道线路配置图

CBTC列车速度及其位置通过LTE无线传输系统实时传输给轨旁自动防护系统，轨旁自动防护系统计算每列车的移动授权并将其实时传输给行进中的列车。列车车载信号系统根据收到的移动授权控制列车追踪运行。CBTC列车追踪运行原则为：列车在运行过程中需满足CBTC列车最小追踪距离要求。若列车与其前方列车的实际距离小于CBTC列车最小追踪距离则减速；若大于CBTC列车最小追踪距离则加速；否则列车保持速度不变。

CBTC列车最小追踪距离有两种计算方法，见式(1)与式(2)。

(1)

(2)

式中min，()为移动闭塞模式下时刻第列车与前方列车最小追踪距离；为列车最大允许速度；()为第列车在时刻的速度；为列车减速度；-为列车长度；SM为安全余量。

从式(1)、(2)可知，采用这两种计算方式，CBTC列车最小追踪距离都为列车制动距离、列车长度与安全余量的总和。不同之处在于在计算列车制动距离时，式(1)假定列车速度为最大允许速度，式(2)采用的速度为列车实时运行速度，因此式(1)计算出的列车最小追踪距离值总是大于或等于式(2)所得值。从信号系统控制精度及提高列车运行效率的角度而言应优先采用式(2)。根据本文研究线路的实际情况，采用式(2)进行CBTC列车最小追踪距离的计算。

3 CBTC列车追踪运行模型

本模型将轨道线路划分为相邻的轨道区段，每个轨道区段内根据相应的运行规则每隔单位步长时间实时更新每列车的状态。

Step1：列车在区段-运行。从车站1下行站台发车点每隔发车间隔-int 发出1列车。列车运行规则如下。

1)列车发车到出清计轴点的过程中，速度不能大于站台限速。

{()<=}：

(+Δ)=min{()+×Δ，}

()=

(3)

式中为站台限速；Δ为步长；为列车加速度。

2)列车追踪距离须满足CBTC列车最小追踪距离。若列车与其前方列车的实际距离小于CBTC列车最小追踪距离则减速；若大于CBTC列车最小追踪距离则加速；否则保持速度不变。

{()()<min，()}：

(+Δ)=max{()-×Δ，0}

{()()>min，()}：

(+Δ)=min{()+×Δ，}

(+Δ)=()

(4)

式中()()为时刻第列车与前方列车的实际距离；min，()为移动闭塞模式下时刻第列车与前方列车最小追踪距离，计算公式见式(2)；为列车减速度；为列车加速度；为列车最大允许速度。

3) 列车在进入弯道前必须采取制动措施使列车驶入弯道起点时速度不大于弯道安全速度。

{()()>()()}：

(+Δ)=min{()+×Δ，}

{()()<=()()}：

(+Δ)=max{()-×Δ，0}

(5)

(6)

式中()()为时刻第列车到前方弯道起点的距离；()()为时刻第列车从当前速度降到弯道安全速度所需的制动距离。

列车在弯道运行时安全速度由弯道曲线半径和路轨超高两个因素决定，弯道安全速度计算公式见式(7)

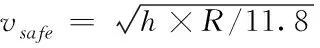
(7)

Step2：列车在区段B-D运行。列车运行规则如下。

1)为限速区段，列车经过点时速度不能大于区段限速值()。

{()()>()()}：

(+Δ)=min{()+×Δ，}

{()()<=()()}：

(+Δ)=max{()-×Δ，0}

(8)

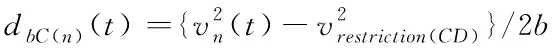
(9)

式中()()为时刻第列车到前方限速点的距离；()()为时刻第列车从当前速度降到CD区段限速值所需的制动距离。

2)相邻列车追踪距须满足CBTC列车最小追踪距离要求，见式(4)；列车速度满足弯道限速要求，见式(5)。

Step3：列车在区段D-G运行。列车运行规则如下。

1)列车越过站台限速点时速度不能大于站台限速。

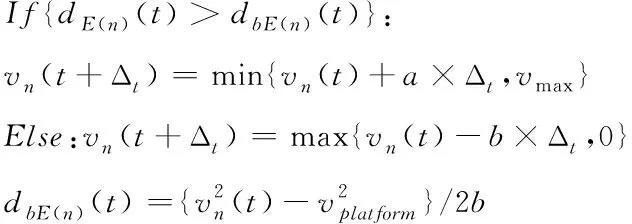
(10)

()()为时刻第列车到前方限速点的距离，()()为列车从当前速度降到站台限速的制动距离。

2)相邻列车追踪距离须满足列车最小追踪距离要求，见式(4)；列车速度满足弯道限速要求，见式(5)。

3)列车须在车站2下行站台停车点精确停车。

{()()>()()}：

(+Δ)=min{()+×Δ，}

{()()<()()}：

(+Δ)=max{()-×Δ，0}

(+Δ)=()

(11)

(12)

式中()()为时刻第列车到停车点的距离；()()为时刻第列车从当前速度减速到零速所需的制动距离。

Step4：列车停在车站2下行站台。

列车在车站2下行站台停站期间进行上、下客作业，停站期间列车速度为0。

Step5：列车在区段G-M运行。

停站时间-(02)结束后，列车从车站2发车点G发车。列车在G-M区段的运行过程与A-G区段一致。

Step6：列车在区段M-N运行。

列车在车站3停站时间-(03)结束后，从点发车，至车尾出清计轴点时驶离系统。在此过程中列车速度不能大于站台限速，见式(3)；相邻列车追踪距离须满足CBTC列车最小追踪距离要求，见式(4)； 列车速度满足弯道限速要求，见式(5)。

每隔单位步长时间Δ，列车位置按式(13)更新一次。

(+Δ)=()+-()×Δ

-()={()+(+Δ)}2

(13)

4 CBTC列车追踪间隔求解

求解CBTC列车追踪间隔的过程，就是寻求连续两列车恰好能够以相同的运行曲线通过线路上各个点的间隔时间。当发车间隔等于追踪间隔时，各列车的运行轨迹完全相同，且列车追踪运行不受前车影响。在追踪间隔时间的求解过程中，如下快速迭代算法减少了求解迭代次数，使求解值尽快向追踪间隔时间收敛。

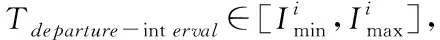
(14)

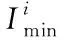
5 案例分析

根据节3建立的CBTC列车追踪运行模型，用Matlab编制程序，对图1所示城市轨道交通线路区段列车追踪运行情况进行仿真。表1为仿真所用列车及信号系统相关参数及运营限制值，轨道区段线路长度及横、纵段面土建数据采用线路实际数值。

在Inter(R)Core(TM)i3-9100CPU3.60GHz处理器、8.00GB内存、Windows10 64位操作系统的计算机上，模拟列车数为100，Matlab R2019b程序运行时间为11.38s。

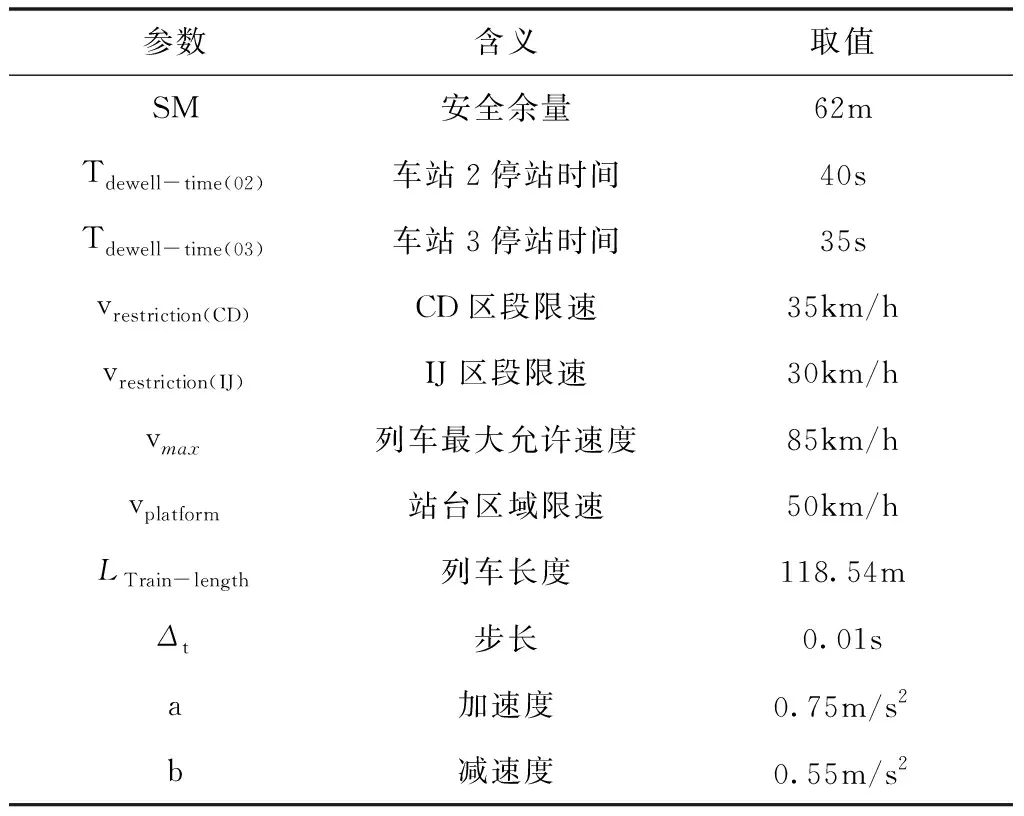
表1 仿真参数取值

5.1 仿真结果

程序运行后自动绘制出列车运行曲线如图2～图5所示。

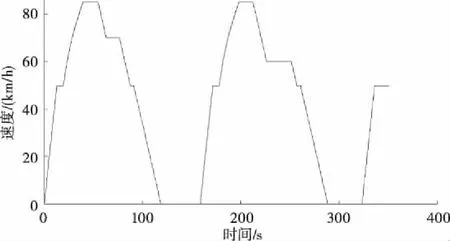
图2 列车时间-速度曲线

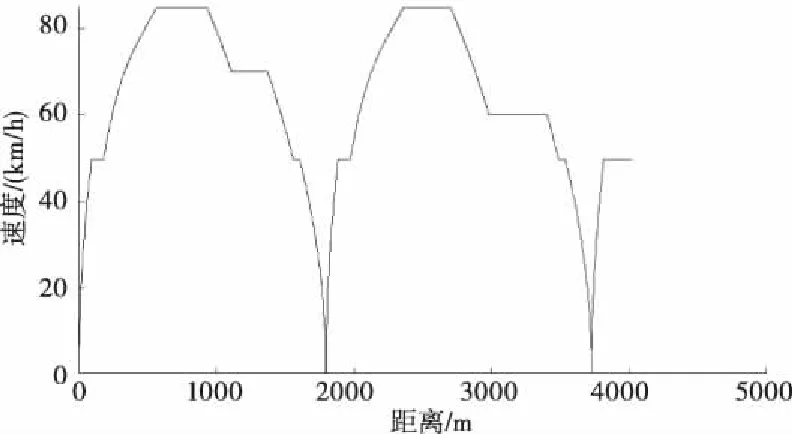
图3 列车距离-速度曲线

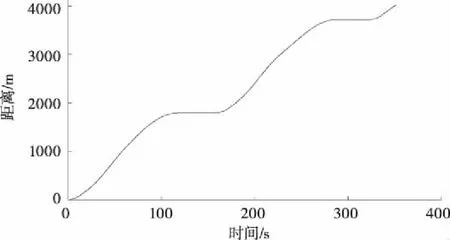
图4 列车时间-距离曲线

图5 列车时间-速度-距离曲线

图2为列车运行时间-速度曲线，图3为列车运行距离-速度曲线，图4为列车运行时间-距离曲线，图5为列车运行时间-速度-距离曲线。图2～图5从不同角度全方位展示了列车时空运行轨迹：列车从车站1下行站台点发出，加速运行直至速度达到站台限速然后匀速运行。待列车出清站台保护区段后，开始加速直至达到最大允许速度并以匀速运行。列车在进入限速区段前开始减速，经过限速区段起点时速度降为区段限速值，之后维持区段限速匀速运行。当列车接近车站2站台区域时开始减速，经过站台区域起点时速度降为站台限速并匀速运行一段时间。之后列车开始进站前的减速过程直至停在车站2下行站台停车点。列车在车站2下行站台停站时间结束后加速出站。之后列车在区段的运行过程与在区段的运行过程一致。列车在车站3下行站台停站时间结束后，加速驶离下行站台停车点，列车速度达到站台限速后维持站台限速运行，直至列车出清站台保护区段，运行结束。图2～图5列车运行曲线与线路特性相符，与列车实际运行情况一致，本文建立的CBTC列车追踪运行模型可反应列车实际追踪运行情况。

5.2 CBTC列车追踪间隔

根据第4节CBTC列车追踪间隔求解步骤，求解得出列车追踪间隔值为108.57s。

可通过不同发车间隔下的列车运行曲线对求解得出的追踪间隔值进行验证。图6显示的是发车间隔-int 设定为60s情形下前20列车追踪运行的时间-距离曲线。从图6可知，从第4列车开始列车在区间停车，原因为发车间隔太短导致列车为满足CBTC列车最小追踪距离而实施制动直至停车。图7显示的是发车间隔-int 设定为108.57s情形下前20列车追踪运行的时间-距离曲线。从图7可知，后续追踪列车运行未受前行列车干扰。发车间隔为108.57s时前100列车的距离-速度曲线如图3所示。从图3可知，所有列车的运行曲线重合，列车运行轨迹完全一致。由此可知列车追踪间隔值为108.57s是合理、可信的。

图6 时间-距离曲线(发车间隔为60s)

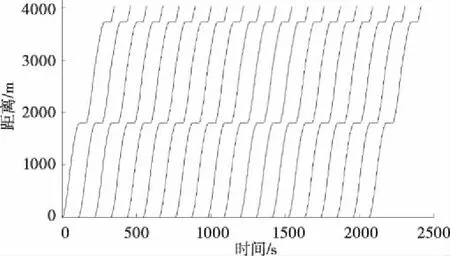
图7 时间-距离曲线(发车间隔为108.57s)

在轨道交通项目现场对图1所示线路进行了CBTC列车追踪间隔能力测试，实测出相邻两列车追踪间隔最长时间为列车在车站3的发车间隔，所测得的追踪间隔为110.25s：利用本模型得出的列车追踪间隔与实测列车追踪间隔仅相差1.52%。

由上可知，本文建立的CBTC列车追踪运行模型能够反应列车实际运行情况，仿真及求解精度较高，可用于城市轨道交通列车追踪间隔方面的研究。

6 结论

本文建立了城市轨道交通CBTC列车追踪运行模型，设计了列车追踪间隔快速迭代求解算法，对城市轨道交通线路CBTC列车追踪运行情况进行了仿真，对列车追踪间隔进行了求解。

1)仿真结果表明CBTC列车追踪运行模型能够真实地反应列车实际追踪运行情况，可用于CBTC列车追踪运行方面的研究。

2)求解模型得出CBTC列车追踪间隔值与现场实测列车追踪间隔相差仅1.52%，CBTC列车追踪间隔求解算法可用于列车追踪间隔方面的研究。

后续需将CBTC列车追踪间隔与出、入段线列车追踪间隔统一起来考虑，立足于整条轨道交通线路对列车追踪间隔进行一体化研究，深入分析追踪间隔影响因素及其作用机理，提出追踪间隔协同优化措施。