交通事故约束下车辆通行最优调度模型仿真

顾 洵，戴 帅

(中国人民公安大学交通管理学院，北京 100038)

1 引言

城市路网多事故应急救援中，因交通拥堵造成应急车辆滞留现象时常发生，严重影响道路交通事故救援效率，尤其近年来，物资运输行业逐渐壮大，城市中货物运输车辆逐渐增多。交通事故发生时，会延长货物运输时长。车辆调度优化由Ramser和Dantzig共同提出，一经提出便成为组合优化领域和运筹学领域的热点问题。科学合理的车辆通行调度不仅能够降低运输成本，而且可以提升客户的认可度，目前车辆通行调度模型已经被广泛地应用于交通线路规划、货物运输以及客户配送等多个领域之中。

卢锦川等人首先结合车辆运输相关参数构建车辆通行调度模型，然后采用非线性扰动因子改进粒子群算法，提高算法全局和局部寻优能力，求解车辆通行调度最优模型。陈友荣等人构建车辆通行调度模型后采用最近邻原则初始化车辆集合，设定车辆通行距离范围，建立二分图并转换矩阵为低维度矩阵，结合实际需求执行KM算法直到生成最优调度模型。马艳芳等人结合模糊需求建立车辆通行调度模型，采用自然数编码构建适应度函数，以两元素优化法作为差分算法变异机制，联合二项交叉算子和贪婪选择算子实现最优调度模型获取。以上方法在构建车辆通行调度模型时没有考虑驾驶员自身特征差异，导致生成的最优调度路径总距离较长，生成最优调度路径所用迭代次数和运行时间较多的问题。

虽然以上研究已经取得了较好的应用效果，但是交通事故发生时，车辆堵塞的问题较为严重，且运输货物车辆体型更大，通行难度也更大。为了解决上述方法中存在的问题，提出交通事故约束下车辆通行最优调度模型研究。

2 车辆通行调度模型构建

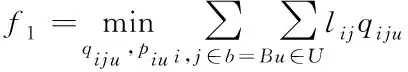
(1)

交通事故下的车辆通行调度问题不仅受外界环境因素影响，同时也与驾驶员自身特征息息相关，通过驾驶速度差异描述驾驶员驾驶经验、风险偏好、道路熟悉程度等个体差异，为使结果具有可比性，将其它外界因素均视为相同，以车辆通行时间最短及通行成本最低为目标分别构建车辆通行调度模型。

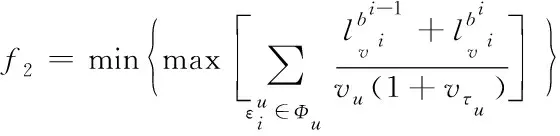
(2)

用表示车辆初始位置，表示驾驶员初始位置，为保证驾驶员初始位置与车辆初始位置相同，设定函数，约束条件如下所示

(3)

其中，(，)=1表示车辆初始位置与驾驶员初始位置相同，反之为0。

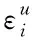
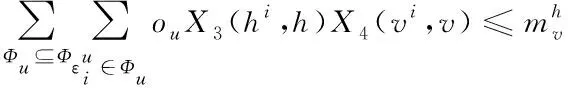
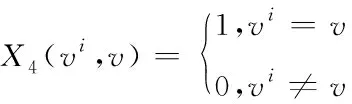
(4)

机械臂要完成相应的抓取工作，必须由步进电机来进行驱动，步进电机的作用是将电脉冲信号转换为相应的角位移或直线位移的设备，它利用电脉冲信号进行控制，当步进电机接收到一个电脉冲控制信号后，就转动一个固定角度或前进一段固定位移。

(5)

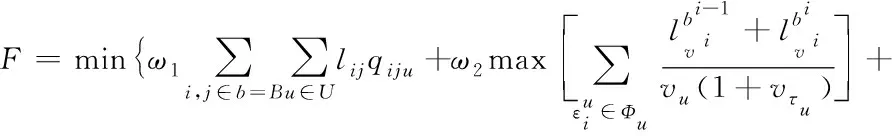
(6)

3 基于自适应模拟退火遗传算法的模型求解

在得到交通事故约束下的车辆通行调度模型后，采用自适应模拟退火遗传算法求解车辆通行最优调度模型。

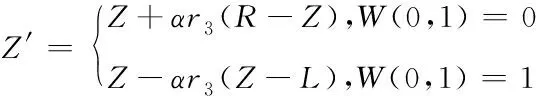
(7)

自适应遗传算法具有优异的全局寻优能力，但其局部寻优能力无法满足寻优需求，因此引入局部寻优能力更好的模拟退火算法对其优化。

模拟退火算法是根据固体退火原理而来的随机算法，在局部寻优中具有优异的表现。引入指数降温法控制温度改变，用表示初始温度，表示温度下降系数，则当前控制温度=()-1，在模拟退火过程中，新解在当前解邻域范围内生成，用和′表示当前解和新解，两者均为种群个体，()表示扰动值，当为时，()≤1，()能够确保′在约束范围内，当→0时，()→0，从而保证算法收敛性，表示(0，1)内随机数。用(′)和()表示和′的适应度值，依据准则计算由变为′的接受概率，如下所示

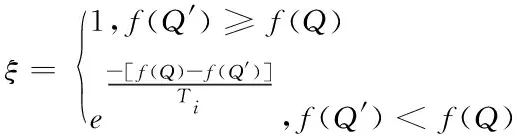
(8)

通过自适应模拟退火遗传算法求解车辆通行调度最优模型的主要流程如下所示

①初始化最小新解接收次数、最大内循环次数、轨道离散参数以及、、、，随机生成初始群体；

②计算全部个体适应度值并记录其中最优适应度个体，拉伸适应度值得到拉伸结果′=exp[-(-)]，引入轮盘赌法选择个体并实行交叉和变异操作；

③设置内循环次数=0，新解接受次数=0，计算自适应遗传算法处理后的个体适应度值，对适应度值最高的前个个体模拟退火，计算()并判定新解接受概率是否符合作为当前解的要求，若符合，则=+1，反之保持不变。若<且<，则=+1，返回步骤①，反之跳出循环，采用适应度值最小的个个体替代退火后个体，开始步骤④；

④采用步骤②记录最优适应度值对应个体替换子代种群中任意一个个体；

⑤若<，则计算当前降温后温度，令=+1，返回步骤②，反之流程结束。

采用以上自适应模拟退火遗传算法能够提升车辆通行调度模型求解能力，从而获取车辆最优调度结果。

4 实验与结果

为了验证交通事故约束下车辆通行最优调度模型仿真的整体有效性，需要设计一次测试实验。调取某市早高峰交通事故的监控录像，如图1所示，随机选取事故现场正在通行的运输货物车辆20台，将运输货物车辆的目的地设置为本次实验的通行调度目的地，经查看监控可知这20台车辆的目的地分布在20km×20km的区域内。

图1 事故现场示意图

以文献[4]提出的基于改进粒子群算法的车辆调度方法和文献[5]提出的基于最近邻原则的车辆调度优化方法为对照方法，测试提出方法的车辆通行最优调度的生成策略的合理性。设定车辆调度中心坐标为(11.0km，15.5km)，目的地相关参数如表1所示。

表1 车辆目的地位置坐标

由于不同车辆通往目的地的路线较多，因此不对生成的调度路径做具体列举。将实验测试过程迭代次数设置为1000次，以所提方法、文献[4]提出的基于改进粒子群算法的车辆调度方法和文献[5]提出的基于最近邻原则的车辆调度优化方法生成的最优调度路径总距离、生成最优调度路径迭代次数和生成最优调度路径运行时间为指标检验三种方法性能，结果如图2～图4所示。

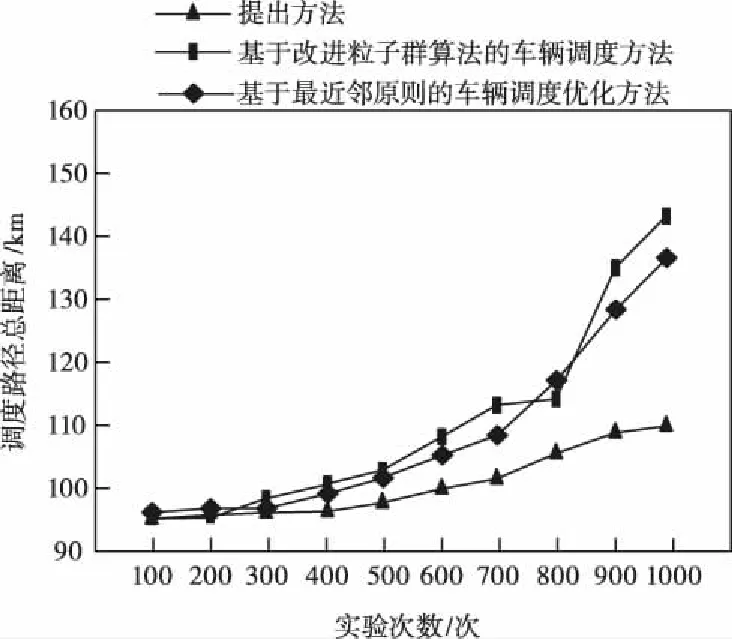
图2 不同方法调度下车辆总距离对比

由图2可以看出，在实现相同运输目标时，所提方法规划的交通事故约束下车辆通行最优调度模型总距离始终小于文献[4]提出的基于改进粒子群算法的车辆调度方法和文献[5]提出的基于最近邻原则的车辆调度优化方法，此实验结果表明所研究模型应用下车辆能够以最短距离到达目的地。因为所提方法在规划车辆通行最优调度模型时不仅考虑外界环境因素的影响，还结合了驾驶员自身特征，以外界干扰和驾驶速度差异共同构建交通事故约束下车辆通行调度模型从而获取最优路径。

图3 不同方法生成最优调度路径时迭代次数对比测试

图4 不同方法调度过程耗时对比测试

由图3和图4可以看出，所提方法在生成总距离短于基于改进粒子群算法的车辆调度方法和基于最近邻原则的车辆调度优化方法的同时迭代次数和运行时间均短于文献方法，说明所提方法获取最优调度路径时的效率最高，更适合用于实际车辆运行调度最优路径规划之中。

5 结束语

为了解决目前存在生成的最优调度路径总距离较长，生成最优调度路径所用迭代次数和运行时间较多问题，提出交通事故约束下车辆通行最优调度模型仿真，结合交通事故和驾驶速度差异构建车辆通行调度模型，采用自适应模拟退火遗传算法求解最优模型。该方法能够有效地缩短生成的最优调度路径总距离，降低生成最优调度路径所用迭代次数和运行时间，为交通事故影响时的车辆通行调度规划奠定基础。