去噪正则化与FFDNet结合的相位恢复算法

金 焱，杨 敏

(南京邮电大学 自动化学院、人工智能学院，江苏 南京 210023)

0 引 言

相位恢复(phase retrieval，pr)是在信号的相位信息缺失的情况下，利用信号的振幅或强度信息复原相位信息，从而恢复出完整图像信息的技术。因为传统相位恢复算法通常使用正反傅里叶变换反复迭代恢复出丢失的相位。但是随着压缩感知技术的流行，众多算法开始使用各种先验知识结合迭代算法实现恢复效果。传统的算法包括使用稀释、平滑等先验结合交替映射、半正定松弛进行恢复，但是这类算法通常只能对特定噪声鲁棒。

将先验知识引入相位恢复的另一种方式是使用模型重构[1]构建正则化模型。通过融合数据保真项和蕴含图像先验知识的正则化项建立pr优化问题，使用优化算法进行求解。此类算法根据噪声不同的分布构建数据保真项，因此通常对不同的噪声都具有鲁棒性。正则化模型将图像先验融入迭代过程，从而提高重建质量和迭代速度。例如即插即用先验[2](plug-and-play priors，PnP)和去噪正则化[3](regularization by denoising，RED)等基于去噪器先验的正则化模型。由于先进去噪器应用成熟且广泛，该类方法潜力巨大。例如Bm3d-prgamp[4]算法融合数据保真项与PnP模型和BM3D[5]相结合的正则化项，求解对应的优化问题。但是传统的去噪器表征能力不足，限制了基于去噪器先验的正则化模型的重建效果。

卷积神经网络(convolutional neural networks，CNN)解决了传统去噪器先验表征能力不足的问题。深度学习的快速发展为解决各类逆问题提供了全新的视角：许多精心设计的网络架构在应用中都具有最先进的性能[6-8]。CNN去噪器先验广泛应用于各类不适定图像恢复问题[9]。在相位恢复问题中，目前提出的prDeep[10]恢复算法使用DnCNN[11]与去噪正则化模型结合。综合了模型优化算法的灵活性和泛用性、判别式学习对复杂先验的强的优势，对噪声鲁棒性强且应用广泛。但是由于DnCNN对不同噪声等级泛用性不是很好，恢复过程依赖多次多套参数的迭代，限制迭代效率的进一步提升。

针对上述恢复算法中存在的问题，该文提出了一种使用FFDNet[12]网络作为去噪器先验结合去噪正则化模型的恢复算法。FFDNet网络具有神经网络强大表征能力，同时提高了对复杂噪声的处理能力，使用图像下采样作为输入参数的方式保证了结果精度和网络效率，提高了改进算法的噪声鲁棒性，提高了重构质量以及迭代效率。

1 使用去噪正则化构建优化模型

使用各式先验知识解决图像不适定问题已经得到广泛应用。相位恢复问题通常可以构建成如下的优化模型。

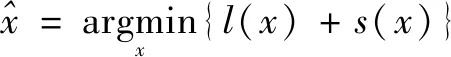
(1)

其中，x∈Rn或x∈Cn，l(x)表示数据保真项，s(x)表示正则化项。构建优化模型依赖数据保真项和正则化项的实现。下面两小节分别介绍文中算法对这两项的具体实现。

1.1 模型重建中数据保真项的实现

在图像处理中，问题的解往往不唯一，所以不适定性相当常见。一般描述如下：

y=Hx+e

(2)

其中，H表示系统的测量矩阵，e表示系统噪声。相位恢复系统通常可以描述为系统的前向算子作用于输入图像，并对输出向量取模的结果。其观测矩阵为非线性映射，可将式(2)替换为：

y=|Ax|+e

(3)

其中，A表示测量系统的前向算子，| · |表示对向量中的每一项取模。将该描述引入式(1)中的数据保真项，得到如下的关于输入项x的优化模型：

(4)

解决此类不适定性问题需要用正则化模型引入先验知识，传统方法如Bm3d-prgamp使用PnP模型构建正则化项，该文使用RED模型构建，1.2节详细阐述RED原理，并比较PnP和RED二者的优劣。

1.2 去噪正则化

RED使用图像自适应拉普拉斯，依赖平滑约束实现对任意的逆问题建立正则化项。正则化项描述如下：

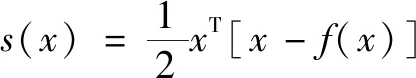
(5)

其中，f(·)表示去噪器，也就是第1节中去噪器所引入的位置。

正则化项主要由原始图像和去噪后的残差的内积组成。作为先验表达式，带入可能的原始图像应当获得较低的值。为了满足该正则化项的最小化，带入RED的原始图像x必须满足以下两个条件之一：x-f(x)趋向于0，即噪声残差相对较小，图像x在去噪模型f(·)的解附近。xT[x-f(x)]趋向于0，x与去噪残差的互相关性较小，即噪声更倾向于与x非相关的白噪声等。

RED对去噪器有所要求。插入RED的去噪器需满足两个要求：局部同质性和强被动性。强被动性要求去噪器的雅各比矩阵的谱半径小于等于1，确保迭代的收敛性：

η(xf(x))≤1

(6)

同质性要求去噪器对于任意的正数c≥0，满足f(cx)=cf(x)，即图像先缩放再去噪的结果应与先去噪再缩放的结果一致。

虽然RED对去噪器有所要求，但是绝大多数的去噪器基本都能满足。而且由于RED对去噪器的同质性要求，使其在迭代方面优于PnP。首先RED在迭代算法上不依赖于ADMM算法。根据RED的同质性要求，可推导出如下等式：

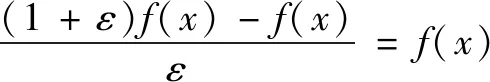
(7)

因此，去噪器f(x)有如下等式：

f(x)=xf(x)x

(8)

于是RED目标函数的梯度可以通过如下方式求解：

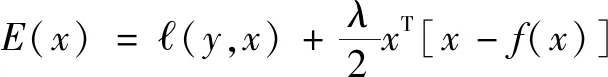
(9)

(10)

其中，式(9)表示RED的目标函数。将式(8)引入式(10)可以得到：

(11)

根据式(11)，以梯度下降法为例，RED的迭代公式如下：

xk+1=xk-μ{x(y,x)+λ[x-f(x)]}

(12)

由此可见，不同于PnP模型，RED不仅可以使用ADMM做优化，也可以使用传统的优化算法提高迭代速度，且可以获得确定的迭代公式。相关工作表明[13-15]，RED模型对各类去噪器先验普遍具有适用性，在图像恢复框架中是最先进的模型之一，并且与深度图像先验结合的研究中拥有更好的恢复效果[16]。

2 FFDNet去噪器先验

RED模型为引入去噪器先验确定下框架基础。利用迭代公式(12)，可以将其中的f(x)替换成各种去噪器先验，而不同的去噪器也会带来不一样的恢复效果。Christopher A. Metzler等人结合RED与DnCNN，提出prDeep算法解决相位恢复问题。该文将prDeep与BM3D-prGAMP进行对比，结果显示prDeep具有更好的PSNR指标。相关研究表明，使用卷积神经网络作为去噪器先验与RED模型结合可以获得更好的恢复效果。

DnCNN作为去噪器先验广泛应用于各种图像逆问题，其结构如图1所示，整个神经网络共17或者20层。第一层使用3×3的卷积核并以零填充(no padding)的方式进行卷积运算，之后使用ReLU非线性激活运算获得第一层的图像输出。之后的每一层都在卷积运算和ReLU非线性激活运算中使用批量归一化(batch normalization，BN)，最后一层只用卷积获得图像最终的残差结果。

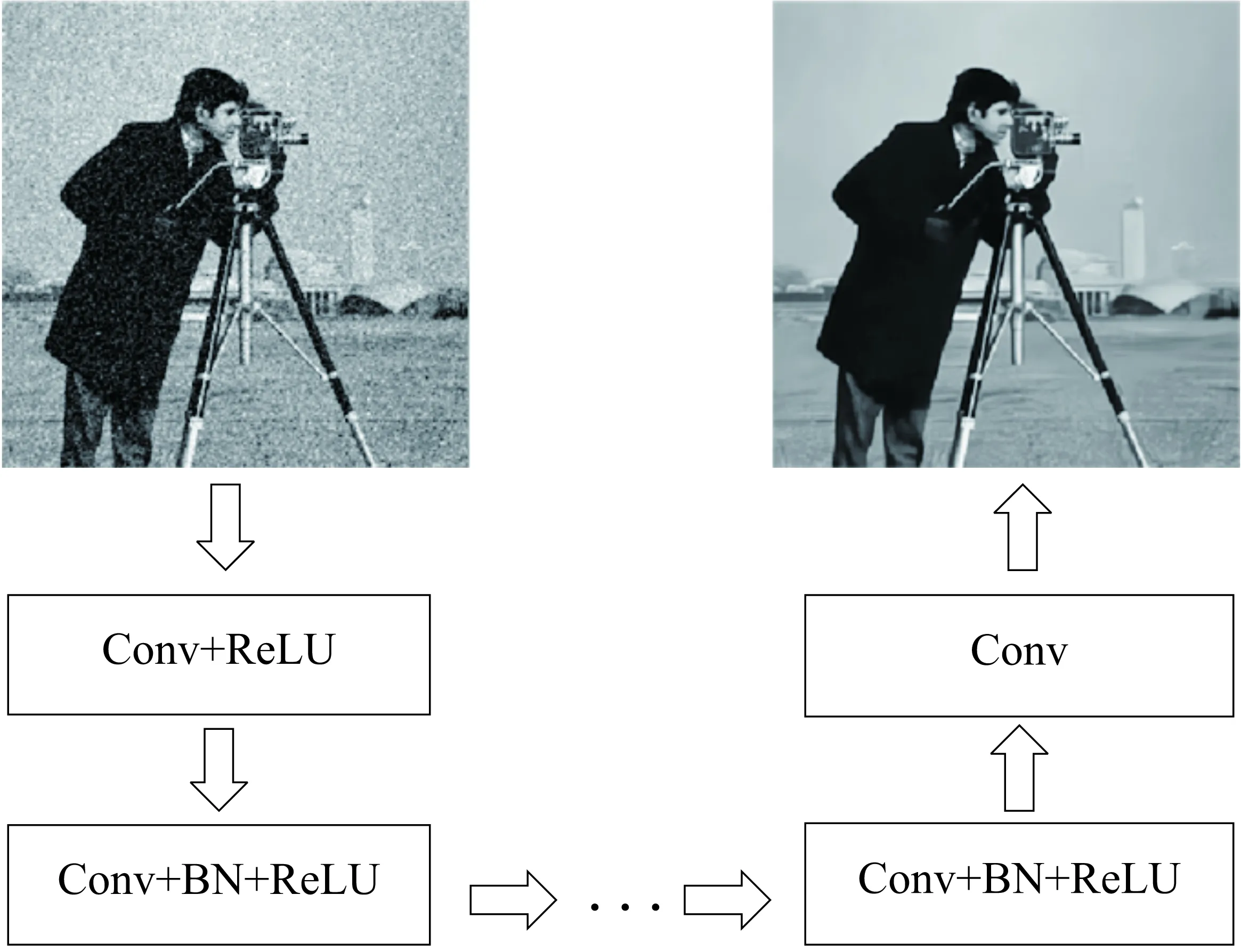
图1 DnCNN结构

DnCNN创造性地使用残差学习与批量归一化训练网络，使得网络较深时仍然有较快的收敛速度。在传统CNN中通常使用SGD(随机梯度下降法)训练，但是受内部协变量偏移的影响，训练速度会变慢。BN在激活函数进行非线性处理之前加入归一化处理，避免层输入逐渐偏移导致激活函数的取值接近上下限，从而发生反向传播时梯度消失的情况[17]。CNN的训练常使用mini-batch，BN通过计算mini-batch的均值和方差再将其归一化。对于一个d维输入x={x1,x2,…,xd}，将每一项归一化：

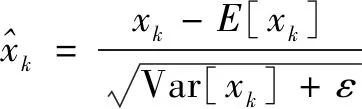
(13)

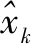
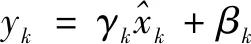
(14)

最终将yk作为结果传播到网络的其他层。而残差学习又解决了深层网络引起的收敛困难以及性能退化的问题[18]，二者相辅相成，使得DnCNN具有良好的去噪效果。

但是DnCNN仍存在一些缺陷，对不同噪声类型和等级自适应性差。在prDeep算法中，为平衡DnCNN在不同噪声水平的恢复效果，不得不使用10个对应不同噪声等级的DnCNN网络参数，在迭代过程中需遍历10个网络以获得最佳重建效果。该缺陷限制了迭代速度和恢复效果。

FFDNet在DnCNN的基础上进行改进，它不仅继承了DnCNN的以上特点，还解决了DnCNN对噪声要求苛刻的问题。DnCNN可以有效地去除均匀高斯噪声，且对一定噪声等级范围的噪声都有抑制作用。但是实际的噪声通常信号依赖、与各颜色信道相关且不均匀，甚至随空间位置变化。FFDNet额外添加了噪声估计图作为输入，结构如图2所示。添加的噪声估计图改进了DnCNN主要针对高斯噪声去噪的问题，使FFDNet可以处理更加真实的噪声。由于DnCNN针对不同噪声等级只能训练多个不同的网络，在恢复过程中需要提前确定图像的噪声等级，或者在不知道输入图像的噪声等级的前提下需要把图像代入众多网络中进行对比，而FFDnet对于不同等级的噪声只需要训练一个网络。除此之外，FFDNet将输入图像下采样，再将输出的图像上采样，这样做的好处是在不影响结果精度的情况下增加感受野，一个15层和3×3卷积的FFDNet网络拥有62×62的感受野，相比之下一个普通的15层CNN网络只有31×31的感受野，而大部分先进去噪方法的感受野一半都在35×35到61×61之间。同时，FFDNet的卷积层数为15层，与17或20层的DnCNN相比减少了网络参数，使得FFDNet更有效率。

图2 FFDNet结构

综合上述优点，该文创新性地将FFDNet与RED相结合，在prDeep算法的基础上改进去噪器，不再使用多个DnCNN网络(prDeep中使用了10个不同参数的DnCNN网络应对各种噪声等级)，而使用一个FFDNet网络实现图像相位恢复。

3 实 验

为了测试文中方法与prDeep以及基于其他去噪器先验方法的相位恢复效果，选取BSD(Berkeley segmentation dataset)中部分图片数据进行对比实验。硬件环境选用Matlab2019b，CPU为Intel Core i7-8750H，8 GB内存，Windows 10系统的笔记本。该文用5组测试图像，分别为barbara(512×512)、cameraman(256×256)、boat(512×512)、peppers(512×512)、Pollen(512×512)，测试图像如图3所示。

图3 测试图像

由于在众多的相位恢复的应用中，散粒噪声是噪声的主要来源[19]，因此本次实验噪声使用泊松噪声来模拟。实验的输入信号分别采用编码衍射[20](coded diffraction)和傅里叶变换，从而获得输入信号的幅值，模拟以图像为信号的相位恢复。之后对幅值信号分别加入不同强度的泊松噪声，并分别使用不同的恢复算法恢复出完整图像。本实验的测试的算法为HIO、BM3D-prGAMP、RED-BM3D、prDeep以及文中算法。实验的部分恢复图像如图4所示，它们分别为128×128的原始图像通过编码衍射获取的幅值信号，并加入噪声强度α=27的泊松噪声后各个算法的恢复效果。

图4 各算法恢复效果对比

为评价算法的整体性能，使用恢复图像的PSNR以及算法的迭代速度作为评价标准。峰值信噪比PSNR主要通过输入真实图像和恢复后的图像，基于二者的误差对恢复的图像效果进行评价，PSNR值越大，代表图像越不失真。

对cameraman图像在不同噪声强度下不同恢复算法的对比如表1所示。每个算法进行4×200次迭代，PSNR取最优效果，时间为4次的平均值，α表示cameraman图像的噪声强度。所有算法都处于相同的硬件环境下。

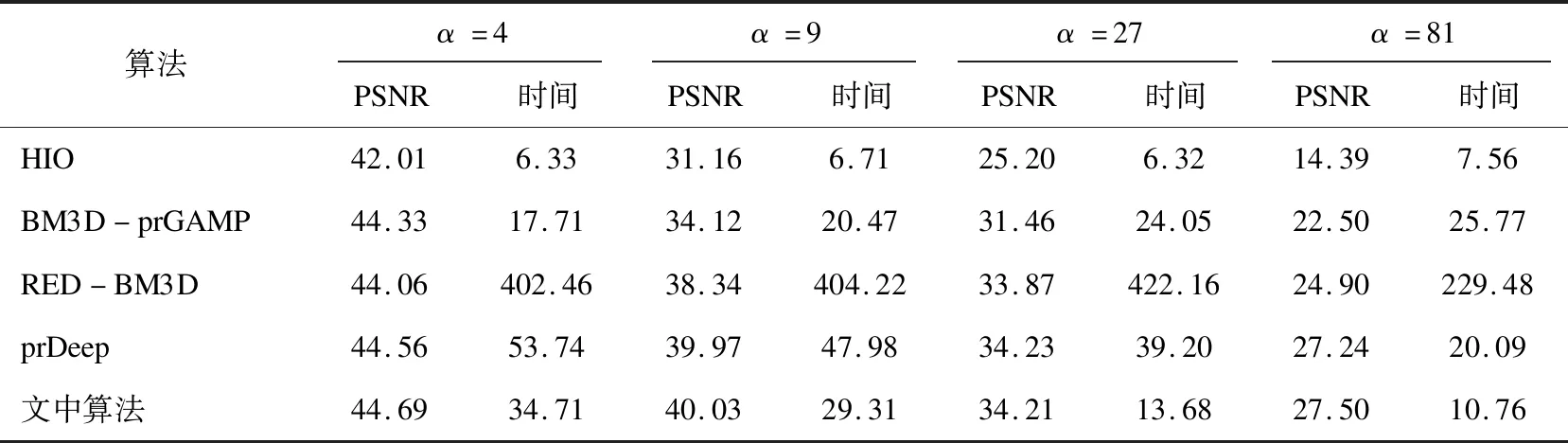
表1 相位恢复算法对比 s

所有测试图像在各个算法中的恢复效果如表2所示。每个算法每张图片进行4×200次迭代，PSNR和时间分别取最优值和平均值，所有测试图像的噪声强度统一为α=27，所有算法使用相同的硬件环境。

表2 不同测试图像的算法对比 s

对比表1和表2可以发现，RED-BM3D、prDeep和文中算法都是使用去噪正则化模型和各自的去噪器结合的算法，它们相较于传统的HIO算法和BM3D-prGAMP算法在峰值信噪比(PSNR)上恢复效果更好。文中算法使用的去噪器为FFDNet，相较于RED-BM3D的去噪器BM3D和prDeep的去噪器DnCNN具有更优的峰值信噪比和更短的迭代时间，说明先进的卷积神经网络去噪器在表征图像特征和先验上的优势。文中算法对比prDeep，在保证图像基本优于prDeep的同时，在迭代速度上有明显的优势，说明FFDNet很好地解决了DnCNN使用多套网络参数应对不同噪声等级从而限制prDeep算法迭代速度的问题。综上所述，文中算法在处理各噪声等级下的相位恢复问题都略优于以上算法。

正则化模型与去噪器先验的结合在现阶段具有很好的重建效果和对噪声的自适应性，且关于去噪器先验在相位恢复中的应用肯定还远不止这些。更多更先进的去噪器例如CBNet、RIDNet等作为先验知识，在处理相位恢复等图像反问题上可能获得更好的恢复效果。

4 结束语

相位恢复问题是仅获取幅值信号的情况下恢复出原信号的相位信息从而恢复出完整的输入信号。现阶段相位恢复算法仍存在对图像特征和先验知识提取不足导致重建效果不充分，或者对复杂噪声自适应性较差限制迭代效率等问题。文中算法在RED与去噪器先验的框架下，利用FFDNet网络的特征表征能力和复杂噪声的自适应性尝试解决这些问题。相比prDeep等算法，迭代更为简单。仿真实验结果表明，该算法在信噪比和效率上都有所提升。在后续研究中，可以尝试引进新的去噪器先验。