9 400 TEU集装箱船实尺度自航性能数值模拟

李兆辉 胡 帆 吴 琼,2 冯 毅,2 孙 群,2

（1. 中国船舶及海洋工程设计研究院 上海 200011； 2. 上海市船舶工程重点实验室 上海 200011）

0 引 言

目前，船舶领域的CFD计算主要集中在模型尺度。由于存在尺度效应，计算结果需要通过经验统计公式换算到实船，这些公式并不具有普适性，而且难以获得实船雷诺数下的流场，对探索新的提升船舶能效的水动力解决方案形成了制约。而直接开展实尺度CFD计算无疑是一个很好的技术途径，但所采用的实尺度CFD计算方法必须经过仔细和独立的验证，才能在业内获得普遍接受和认可。

国外：2006年，HANNINEN等分析了EFFORT项目的算例，验证了RANS 求解器用于实尺度数值模拟的可行性；2009年，BHUSHAN等基于URANS 求解器，证明了在考虑壁面粗糙度和压力梯度影响下，两点多层壁面函数模型尺度与实尺度数值模拟中的通用性；2011年，CASTRO等采用重叠网格研究了实尺度下螺旋桨和船体的相互作用，并分析了船模尺度和实尺度对船的边界层和螺旋桨推进性能的影响。

国内：2015年，陈天福等采用结构化网格和非结构化网格相结合的计算方法，进行了实尺度导管螺旋桨的敞水性能数值模拟；2016年，尹崇宏等应用改进的DES 模型（IDDES），采用CFD 方法同时对模型尺度和实尺度的32万t VLCC 进行阻力预报，并分别与RANS 的计算结果和试验结果进行比较分析；2016年，李亮等采用RANS方法和VOF模型，开展了考虑自由液面的实船自航性能的数值模拟，分析发现自航点转速和伴流分数尺度效应明显；2018年，陈骞等进行了实尺度阻力模拟，并与水池试验结果的实尺度换算数值进行对比，指出实尺度下伴流更加均匀。

本文采用体积力和滑移网格这2种螺旋桨模拟方式对9 400 TEU集装箱船进行实尺度自航性能数值模拟，分别考察湍流模型、网格划分、最大非线性迭代次数、时间步长、激励盘参数及动区域大小等因素对计算结果的影响，并与模型试验换算及实船试航结果对比，分析2种螺旋桨模拟方式的优劣并验证实尺度自航性能数值模拟的可靠性。

1 数学模型

本文使用FINE/Marine商用软件，它是NUMECA公司推出的船舶与海洋工程专业CFD软件包包括网格生成器HEXPRESS、黏流求解器ISISCFD和后处理器CFView。FINE/Marine软件基于RANS方法求解船体周围流场，使用流体体积函数（volume of fluid，VOF）方法捕捉自由液面，采用动网格技术处理船舶姿态变化。

1.1 控制方程

FINE/Marine的求解器ISIS-CFD流动控制方程为不可压缩非定常雷诺平均N-S方程（RANS），采用有限体积法对输运方程进行空间离散。在等温条件下，不可压缩黏性流体的质量和动量守恒方程如下：

1.2 湍流模型

在雷诺平均N-S方程中，由于雷诺应力是未知的，因此方程的封闭需要定义湍流雷诺应力。根据对雷诺应力的模化方式不同，湍流模型分为涡黏模型和雷诺应力模型。涡黏模型基于BOUSSINESQ涡黏假设，引入湍流涡黏系数，建立雷诺应力与平均应变率的关系；雷诺应力模型则直接利用雷诺应力输运方程，对方程中相关项进行模化使方程封闭。由于RANS方法采用时间平均忽略了湍流脉动，湍流模型也不具备普适性；而大涡模拟（large eddy simulation，LES）对大尺度涡结构直接计算，对小尺度涡构造亚格子应力模型进行模化，从而获得流动的动态特性。但是，LES对网格尺寸的要求限制了工程应用，1997年，SPALART提出了一种混合RANS/LES的分离涡模型（detached eddy simulation，DES）。

本文分别使用涡黏模型、雷诺应力模型和分离涡模型这三类湍流模型中的（SST-Menter）模型、EASM模型和DES-SST模型。

1.3 VOF方法

ISIS-CFD求解器采用VOF方法捕捉自由液面，VOF方法把空气和水作为两相流体进行计算，多相流的体积分数守恒方程如下：

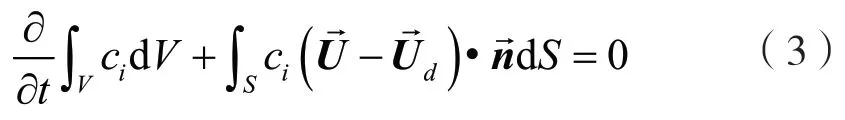
式中：c是第相体积分数。当空间中全部是第相流体时，c=1；而没有第相流体时，c=0。显然体积分数介于0～1时，表示是多相混合流体。由于船舶CFD计算中通常只包含空气和水两相，因此将c=0.5处定义为交界面。

多相混合流体的物性参数（黏性和密度）是各组成相的物性参数（黏性μ和密度ρ），由本构关系得到：

1.4 体积力方法

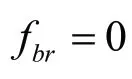
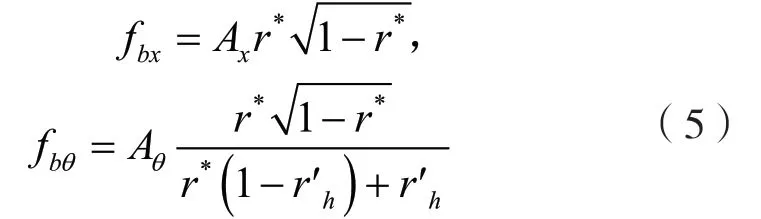
式中各参数表达式为：

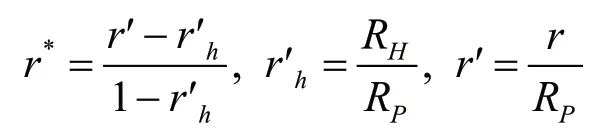
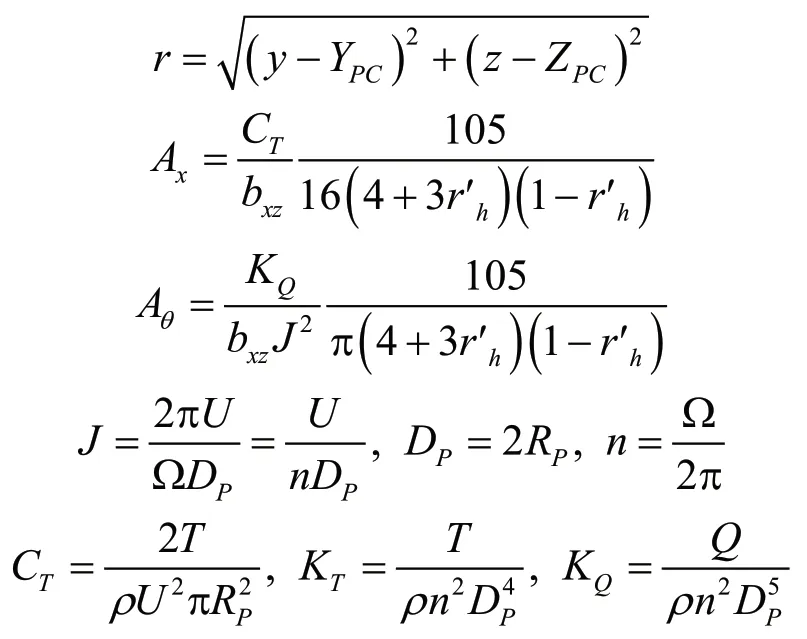
式中：K和K分别是推力系数和转矩系数；是进速系数；是转速，r/s；Ω是旋转速度，rad/s；R是螺旋桨半径，m；R是桨毂半径，m；是参考速度，m/s；b是投影到-平面的平均弦长，m（或激励盘厚度）；Y和Z是螺旋桨中心坐标。

2 计算模型

2.1 计算对象及工况

以9 400 TEU集装箱船为计算对象，船体主尺度和螺旋桨几何参数分别如表1和表2所示。

表1 船体主尺度

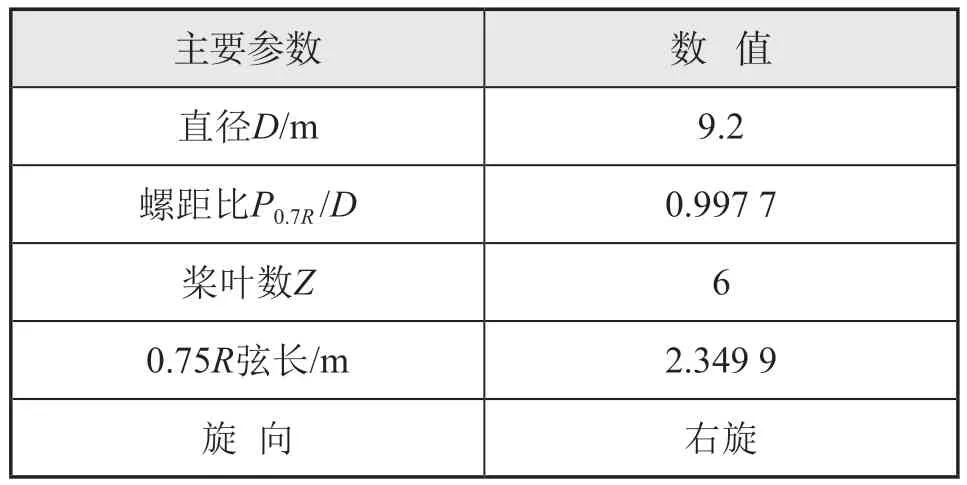
表2 螺旋桨几何参数

该螺旋桨是与设计桨敞水性征相近的备用桨，本文数值计算和模型试验采用的是备用桨，而实船试航采用的是设计桨。计算时除船体外，包含的附体有艏侧推孔及舵（含假舵及舵球）。该集装箱船及其附体的几何外形如图1所示，笛卡尔坐标系下，以尾垂线和基平面交点为原点。轴沿船长方向，正向指向船首；轴沿船宽方向，正向指向船的左舷（从后往前看）；轴沿船深方向，正向垂直向上。

图1 几何模型及坐标系

对几何模型进行实船尺度的数值计算，计算工况如表3所示，雷诺数=2.693 6×10，弗劳德数=0.215。

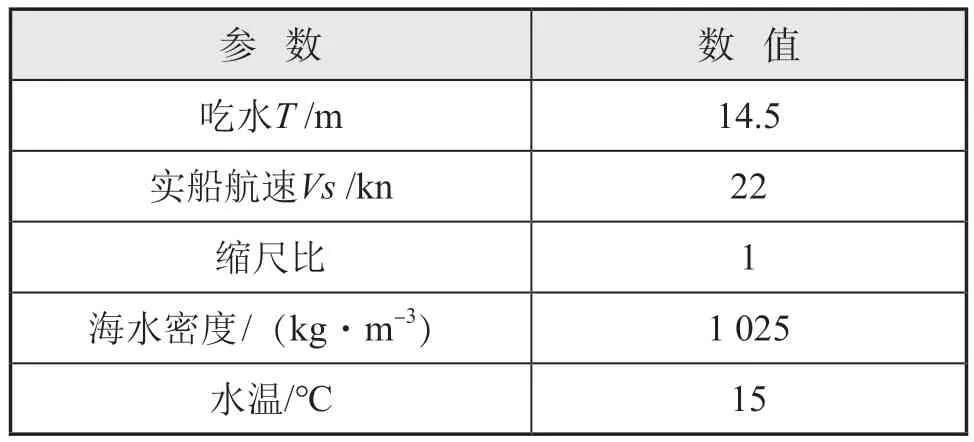
表3 计算工况

2.2 计算域及边界条件

由于螺旋桨的转动带动周围流体产生旋转，导致船体周围流动不对称，因此实尺度自航性能计算选取全船进行计算。计算域如图2所示。

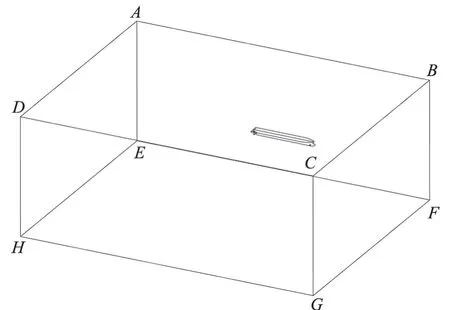
图2 计算域

计算域各边界面距坐标原点的距离如表4所示，L为垂线间长。计算域的长度为5L，宽度为4L，高度为2L。

计算域边界条件设定见表4。船体表面除甲板外为固壁非滑移边界，使用标准壁面函数，甲板为滑移边界。

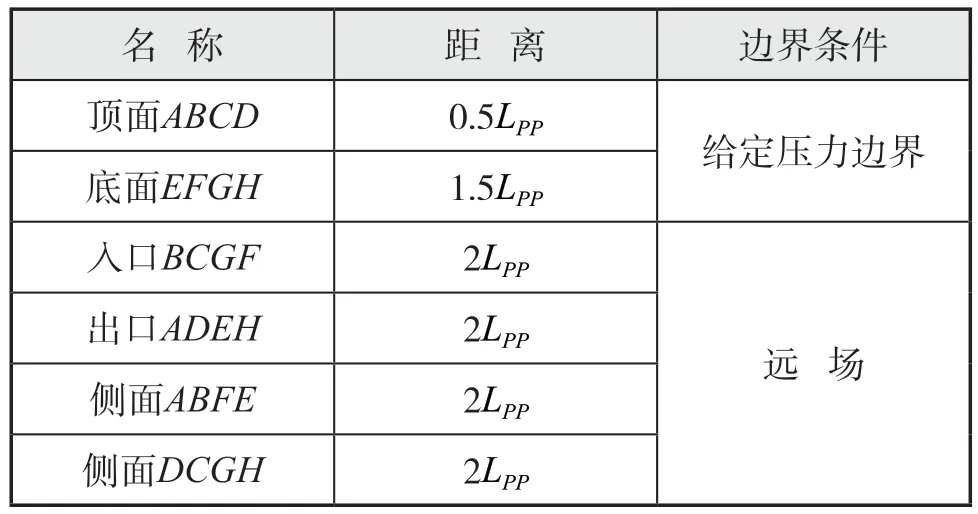
表4 计算域大小与边界条件

2.3 网格划分

采用非结构化六面体网格生成工具HEXPRESS进行网格划分。图3为计算域全局网格、船体表面网格及边界层网格分布。

图3 计算域、船体表面及边界层网格

实尺度下雷诺数较大，边界层内湍流剧烈，与模型尺度相比需要布置更多的网格层数。采用壁面函数处理近壁面一般要求第1层网格的无量纲化壁面距离满足30＜＜200，但是在实尺度下满足该要求将导致网格数激增。2020年，苏玉民等分析了国内外实尺度船舶快速性数值计算的，建议采用的范围为30～500。第1层边界层网格的可以按式（6）估算：

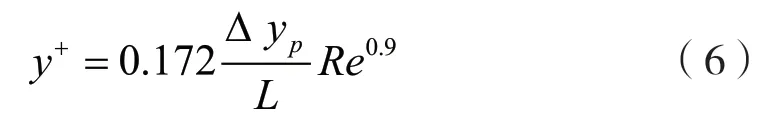
式中：为特征长度，m，一般取=L；Δy为第1层边界层网格厚度，m。

2.4 激励盘设置

采用激励盘即体积力的方法进行实船尺度自航性能数值计算，施加的体积力由实桨的敞水性征值（如图4所示）确定，本文中实桨的敞水性征值由敞水试验结果利用1978年ITTC推荐的修正公式换算得到。对于试验数据点之间的敞水性征值，ISIS-CFD求解器会自动利用插值获取。对于实船尺度数值计算，不需要考虑摩擦阻力修正。激励盘设置在螺旋桨中心点，激励盘厚度参考螺旋桨桨叶侧投影轮廓确定，内半径为桨毂半径，外半径为螺旋桨半径。

图4 桨模经ITTC修正到实桨的敞水性征曲线

FINE/Marine对于采用激励盘来确定自航点有2种计算方式：一种是给定航速求解螺旋桨需要的转速，另一种是给定螺旋桨的转速求解可以达到的航速。后者航速的迭代需要不断模拟船体加速的过程，因此计算相对耗时，而前者转速的迭代只需要对敞水数据进行插值。本文选取第1种计算方式，通过不断改变转速直至船体阻力与激励盘推力平衡来确定实船自航点。最终设置的激励盘如图5所示，与螺旋桨旋转方向保持一致即为右旋。

图5 激励盘示意图

2.5 滑移网格设置

采用滑移网格进行自航性能数值计算时，需在螺旋桨周围设置动区域，动区域设置为圆柱体，如图6所示。动区域需包括整个螺旋桨几何，其直径厚度不宜过小，以避免动区域外边界到螺旋桨距离过小导致其附近网格质量较差的问题。动区域与螺旋桨一同转动，动区域外边界与静区域内边界产生相对旋转，为实现计算过程中静区域与动区域在交界面进行数据交换，将静区域与动区域交界面设置为完全非匹配边界条件（full non-matching boundary）。螺旋桨及尾轴表面设置为固壁非滑移边界，使用标准壁面函数。

螺旋桨网格划分时，对桨叶导边、随边和叶根处进行加密，如图6所示。

图6 螺旋桨表面网格及动区域

采用真实桨的自航数值模拟确定实船自航点，通常是在给定航速后计算多个螺旋桨转速，根据船体阻力和螺旋桨推力随螺旋桨转速变化曲线确定2个曲线交点即为该航速的自航点。该方法由于需要计算多个转速，相对耗时并且存在插值误差。FINE/Marine开发了一种动态控制器，在计算过程中自动调整转速，使作用在船体上的合力为0，从而在一次计算中确定自航点，但仍然比固定航速和转速时耗时更多。

因此，本文在开展基于滑移网格的实尺度自航性能数值计算方法研究时，首先固定航速和转速，以收到功率P为指标评判计算精度；然后根据数值计算方法研究结果，选取合适网格划分方案和数值参数，开启控制器，在给定航速的情况下预报实船自航点；最后，与体积力方法预报的实船自航点进行分析对比。

3 基于体积力的实尺度自航性能数值计算方法研究

3.1 网格依赖性研究

针对边界层网格的不同划分方案进行计算，分析边界层网格划分对基于体积力自航性能计算结果的影响。

选取第1层边界层网格厚度分别为0.000 02L、0.000 01L和0.000 005L，根据公式（6），其计算前预估值分别为1 058、528和264。相应边界层网格计算后得到的船体表面值实际分布如图7所示。

图7 船体表面y+分布

船体湿表面（水下部分）平均值依次为714、359和180，表明采用公式（6）估算的值偏大。船体表面高区集中在舵迎流面，船身大部分区域在相应平均值左右。

如表5所示，第1层边界层网格厚度0.000 02L时预报的螺旋桨转速偏差较大，而第1层边界层网格厚度为0.000 01L和0.000 005L时，两者计算精度相近。因此，根据公式（6）在约为500计算得到的第1层边界层网格厚度用于实尺度数值计算时，可达到较高计算精度。综合计算时间和精度，其他研究中，将船体表面第1层边界层网格厚度设置为0.000 01L。

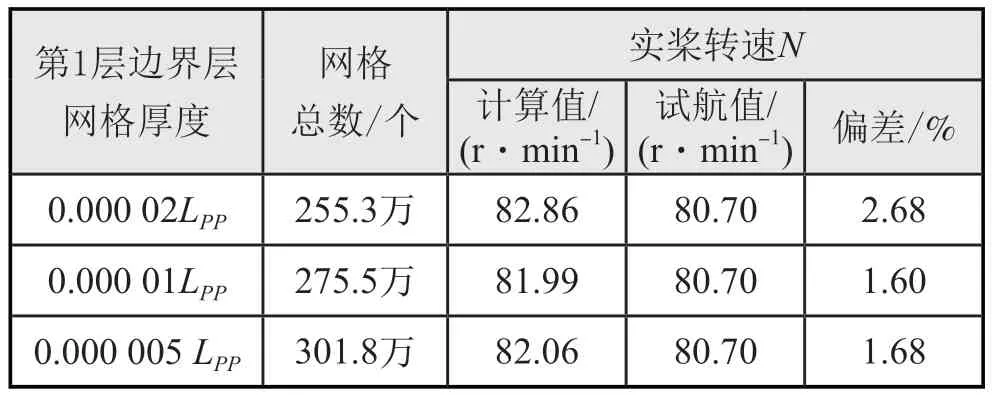
表5 不同边界层网格方案计算结果

3.2 湍流模型依赖性研究

选取涡黏模型-（SST-Menter）、雷诺应力模型EASM和分离涡模型DES-SST，分析湍流模型对自航性能计算结果的影响。

如表6所示，-（SST-Menter）模型和EASM模型的螺旋桨转速预报精度相差不大，DES-SST模型螺旋桨转速预报精度更高，偏差为0.52%。每次迭代所消耗计算资源从小到大依次为-（SSTMenter）模型、EASM、DES-SST模型，在相同设置下，-（SST-Menter）模型计算耗时最短。综合计算时间和精度，在其他研究中，湍流模型设置为-（SST-Menter）模型。

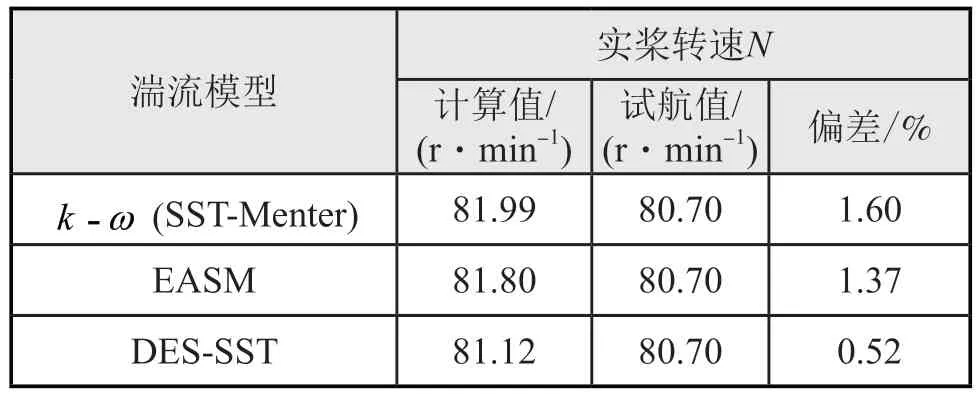
表6 不同湍流模型计算结果

3.3 激励盘几何参数影响研究

激励盘几何参数设置包括中心点坐标、厚度、内半径和外半径。激励盘中心点坐标为螺旋桨中心点坐标，外半径为螺旋桨半径，这两者取值是确定的；激励盘内半径为桨毂半径，而桨毂半径通常沿桨轴方向是变化的；激励盘厚度需要参考螺旋桨桨叶形状，而各种类型螺旋桨水动力性能各异，其厚度值选取难以统一。因此，本文专门考察激励盘内半径和厚度的取值对自航性能计算结果的影响。

桨毂半径沿桨轴方向由0.800 m变化到0.850 m。另外，如果桨毂存在时，需保证激励盘不与物面相交，因此要增加考虑激励盘内半径大于桨毂最大半径的情形，于是选取3个内半径：0.80 m、0.85 m和0.90 m。

如表7所示，在桨毂半径变化范围内的内半径取值对计算结果影响很小，内半径越大预报转速越高。内半径为0.80 m时，螺旋桨转速预报偏差最小。由于本文中用于体积力自航计算的船体几何中不包含桨毂，内半径按桨毂最小半径取值时不存在激励盘与桨毂相交的情况，所以在其他研究中，将激励盘内半径设置为该值。

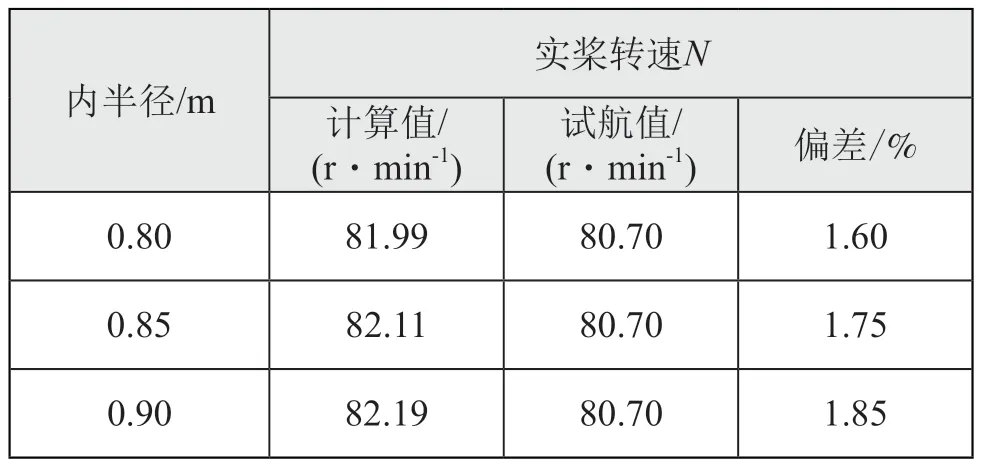
表7 不同激励盘内半径计算结果

FINE/Marine推荐的激励盘厚度为0.1，实际上本文螺旋桨桨叶侧投影轮廓厚度约为0.15，于是选取3个厚度：0.92 m(0.1)、1.38 m(0.15)和1.84 m(0.2)。如表8所示，激励盘厚度对计算结果影响较大，激励盘厚度偏大或偏小均导致螺旋桨转速预报偏差增大，而根据螺旋桨桨叶实际厚度确定的激励盘厚度计算精度最高，所以在其他研究中，将激励盘厚度设置为1.38 m(0.15)。

表8 不同激励盘厚度计算结果

3.4 数值计算控制参数影响研究

针对不同的时间步长和最大非线性迭代次数进行计算，分析这些数值计算控制参数对自航性能计算结果的影响。

根据0.01L /、0.005L /和0.002 5L /选取3个时间步长：0.25 s、0.125 s和0.062 5 s。如表9所示，在（0.002 5～0.01）L /范围内时间步长对计算结果影响不大，在其他研究中，将时间步长设置为0.125 s（0.005L /）。

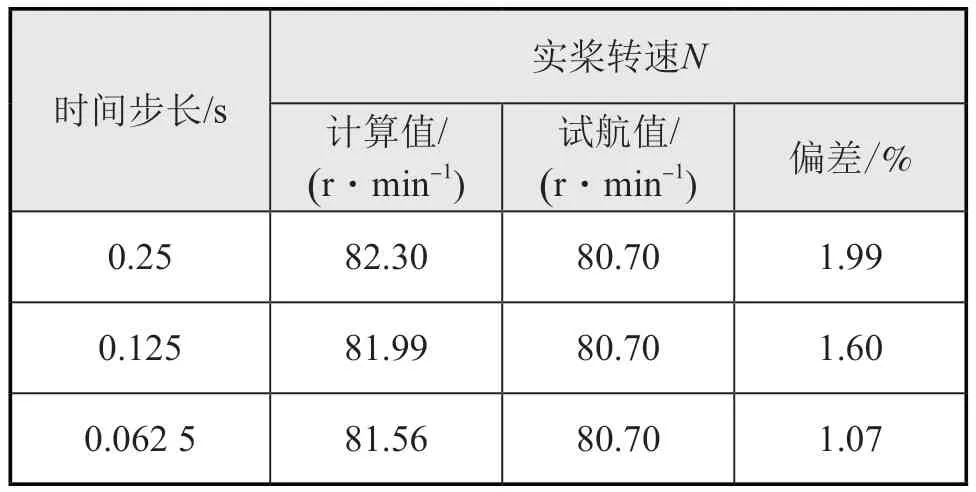
表9 不同时间步长计算结果

最大非线性迭代次数指每个时间步长内在求解非线性控制方程过程中所设置的最大迭代次数。选取3个最大非线性迭代次数：5次、10次和15次。如下页表10所示，最大非线性迭代次数对计算结果几乎无影响，而计算时间与迭代次数正相关。综合计算时间和精度，在其他研究中，最大非线性迭代次数设置为5次。

表10 不同最大非线性迭代步数计算结果

4 基于滑移网格的实尺度自航性能数 值计算方法研究

4.1 网格依赖性研究

采用滑移网格模拟真实桨转动时，由于螺旋桨相对船体旋转，其螺旋桨表面流动与船体表面流动存在较大差异。因此，专门针对螺旋桨表面边界层网格的不同划分方案进行计算，分析螺旋桨表面边界层网格划分对基于滑移网格自航性能计算结果的影响。船体表面第1层边界层网格厚度设置为0.000 01L。

计算过程中，除航速固定为22 kn外，为节省计算时间，未启用转速控制器，而直接将螺旋桨转速设置为与实船试航结果相同，即80.7 r/min。

螺旋桨表面第1层边界层网格厚度依次设置为0.000 02L、0.000 01L和0.000 005L，相应边界层网格计算后得到的螺旋桨表面值实际分布如图8所示，螺旋桨表面平均值依次为1 768、888和454。

图8 螺旋桨表面y+分布

螺旋桨表面高区位于桨叶导边靠近叶梢侧，低区位于桨毂表面靠近舵球侧，桨叶表面沿径向由叶根到叶梢逐渐增加。

数值计算结果与实船试航结果的对比如表11所示，螺旋桨收到功率均用实船试航结果进行了无量纲化。

表11 不同螺旋桨边界层网格方案计算结果

对比发现不同螺旋桨边界层网格方案螺旋桨收到功率偏差预报变化幅度达到6.99%，表明螺旋桨边界层网格对自航计算精度影响较大。螺旋桨第1层边界层网格厚度为0.000 01L时螺旋桨收到功率预报精度最高，几乎与实船试航结果完全吻合。综合计算时间和精度，其他研究中，将螺旋桨表面第1层边界层网格厚度设置为0.000 01L。

4.2 湍流模型依赖性研究

选取不同的3种湍流模型，分析湍流模型对自航性能计算结果的影响。如表12所示，-（SSTMenter）模型螺旋桨收到功率预报精度最高，在其他研究中，湍流模型设置为-（SST-Menter）模型。

表12 不同湍流模型计算结果

4.3 动区域几何参数影响研究

采用滑移网格进行自航计算时，需要在螺旋桨周围建立动区域。动区域除了包围螺旋桨之外，要避免船体相交，如果动区域半径过小会使螺旋桨叶梢距离动区域圆柱面过近，还会使船尾表面距离动区域圆柱面过近，这2种情况均会限制动区域附近物面网格尺寸，进而影响网格质量，由于船尾布置后者相对前者更少出现。因此，本文专门考察动区域半径的取值对自航性能计算结果的影响。

根据螺旋桨半径与船尾几何形状，选取3个动区域半径：4.8 m、5.0 m和5.2 m。如表13所示，动区域半径会影响其周围网格划分，对计算结果影响较大，动区域半径为4.8 m螺旋桨收到功率预报偏差最大，另外两者偏差相近，所以动区域半径选取时不宜过小。动区域半径为5.0 m时，螺旋桨转速预报偏差最小，在其他研究中，将动区域半径设置为该值。

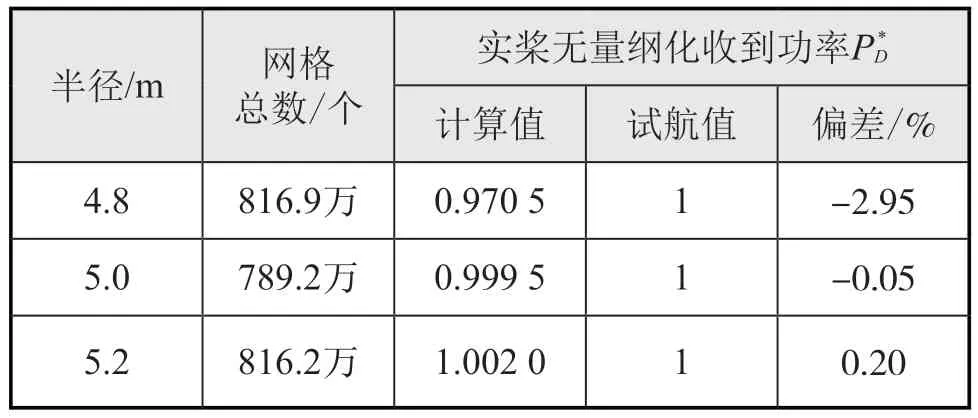
表13 不同动区域半径计算结果

4.4 数值计算控制参数影响研究

同样针对不同的时间步长和最大非线性迭代次数进行计算，分析这些数值计算控制参数对自航性能计算结果的影响。

采用滑移网格进行自航计算时，为了加快收敛，先采用大的时间步长获得初解，然后转为小的时间步长获得精确解。大的时间步长参考L /，此处与体积力方法一致取为0.005L /，即0.125 s；小的时间步长参考螺旋桨旋转周期1/，由于螺旋桨转速为80.7 r/min时，转过1°所需时间约为0.002 s，于是选取3个时间步长：0.004 s、0.002 s和0.001 s。如表14所示，在螺旋桨转过0.5°～2°所需时间范围内，时间步长对计算结果影响很小，在其他研究中，将时间步长设置为0.002 s。

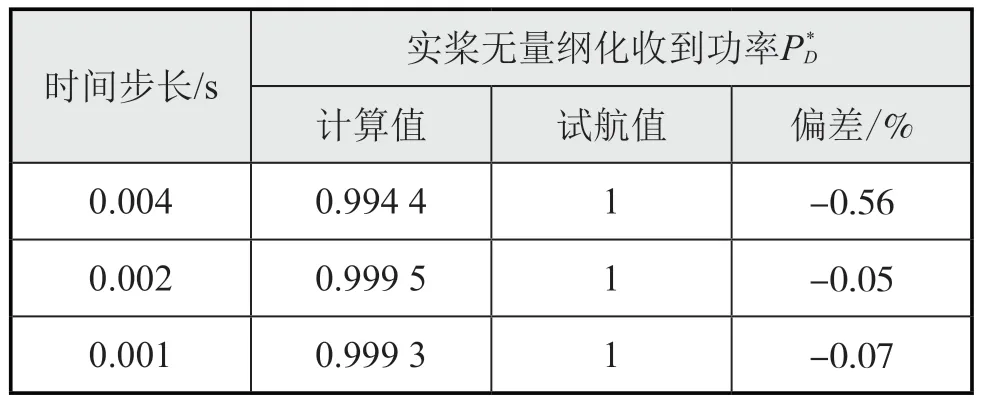
表14 不同时间步长计算结果

同样选取3个最大非线性迭代次数：5次、10次和15次。如表15所示，最大非线性迭代次数较小时，螺旋桨收到功率预报偏差较大，另外两者偏差相近。这是由于真桨旋转使船尾流场更加复杂，导致收敛变慢，所以有必要增加最大非线性迭代次数。综合计算时间和精度，在其他研究中，最大非线性迭代次数设置为10次。

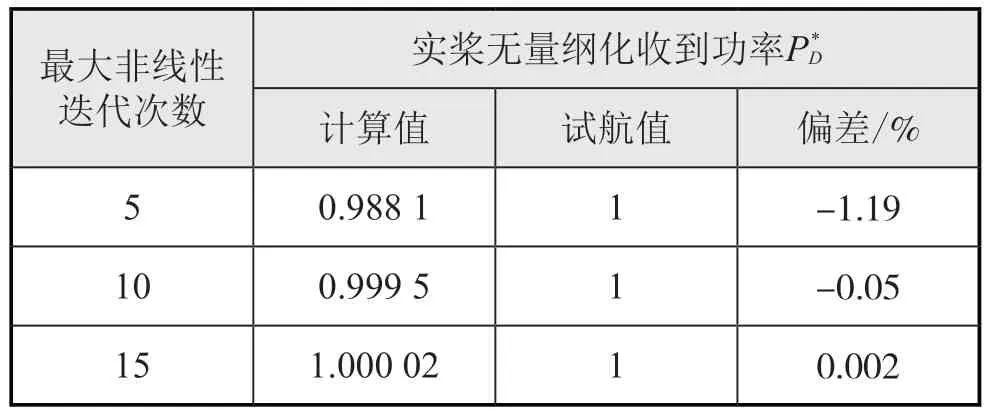
表15 不同最大非线性迭代步数计算结果

5 实船自航性能预报结果分析

为了对比体积力方法和滑移网格方法的实尺度自航性能数值计算结果，针对基于滑移网格的实尺度自航性能数值计算，在给定航速22 kn下，开启转速控制器，根据船体阻力与螺旋桨推力平衡求解实船自航点。

2种方法所预报实船自航点螺旋桨转速、收到功率如表16所示。船模自航试验结果根据1978年ITTC方法换算到实船。与实船试航结果相比，2种方法计算得到的螺旋桨转速、收到功率与试验换算结果偏差更小，其中实桨转速偏差均在3%以内，实桨收到功率偏差均在7%以内。

表16 2种方法螺旋桨转速与收到功率的计算结果

由于计算和试验采用的是与设计桨敞水性征相似的备用桨，而实船试航采用的是设计桨。船舶自航时，螺旋桨在船处于非均匀来流条件下工作，设计桨与备用桨虽然在均匀来流中的敞水性能相近，但是在非均匀来流中它们性能可能存在差异，从而导致计算结果与实船试航结果的偏差比其与试验换算结果的偏差大。体积力方法得到的螺旋桨转速、收到功率相比于滑移网格方法更接近试验换算结果和实船试航结果，表明实尺度下采用体积力模型替代真实螺旋桨进行实船性能预估仍能具有较高精度。

结合图4的实桨敞水性征曲线与实尺度阻力性能数值计算结果，2种方法根据各自实尺度自航性能数值计算结果，采用等推力法求解的自航推进因子如表17所示。表中：是根据等推力法从实桨敞水性征曲线插值所得进速系数、K是推力系数、K是转矩系数、t是推力减额、w是伴流分数、η是推进效率、η是船身效率、η是相对旋转效率、是敞水效率。

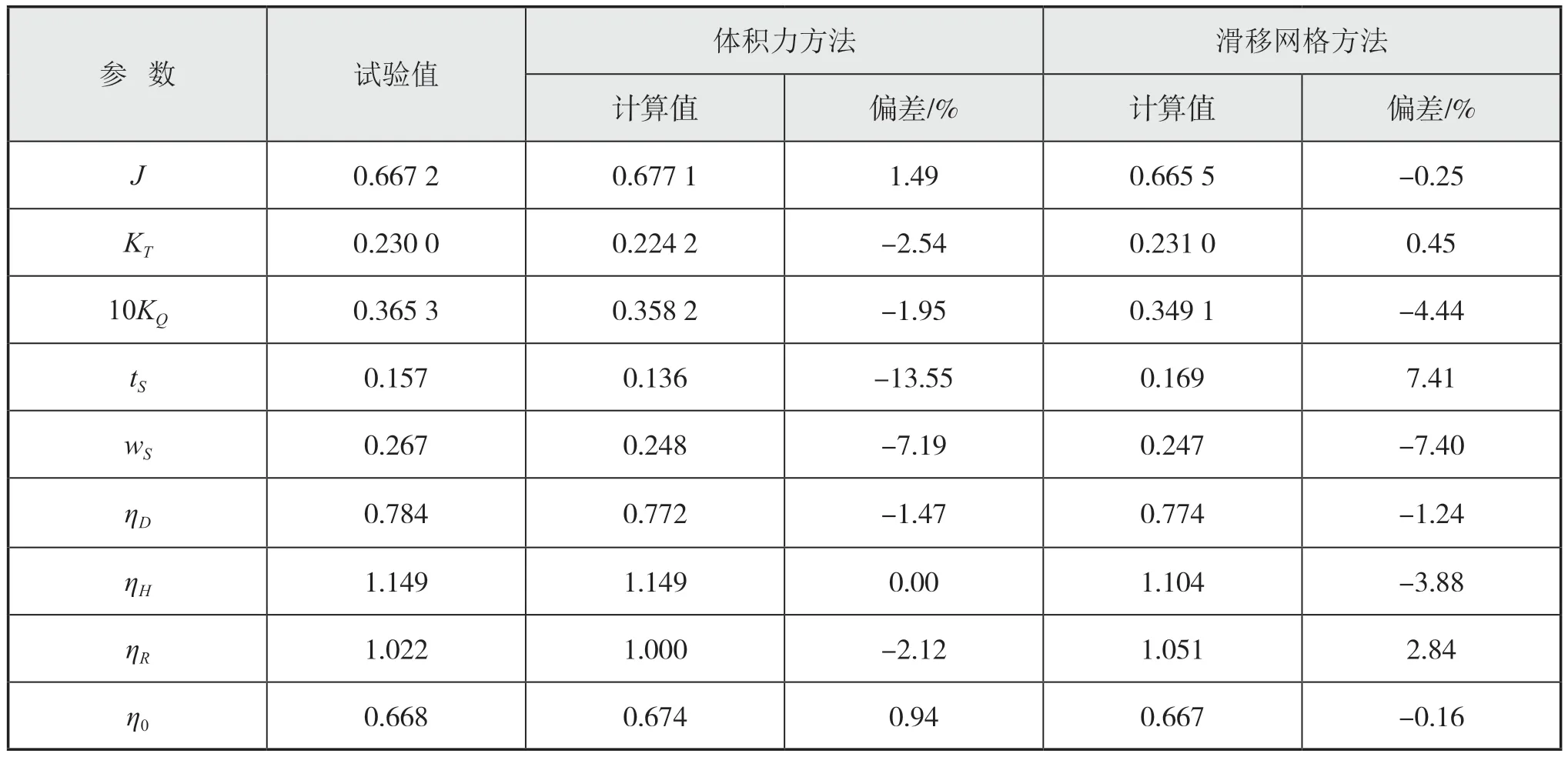
表17 2种方法推进因子的计算结果

除推力减额和伴流分数外，2种方法计算得到的其余各项推进因子与试验换算偏差值均在5%以内，体积力方法过于低估了螺旋桨推力，而滑移网格方法过于低估了螺旋桨转矩，两者计算推进效率相近。体积力方法不能得到相对旋转效率，因为无法确定螺旋桨在船后时的转矩，因此体积力方法的相对旋转效率η=1。

2种方法计算得到的尾流场涡结构如下页图9所示，取速度梯度二阶不变量=5的等值面。体积力方法捕捉到了毂涡，在桨盘面处的涡环表明体积力模拟出了螺旋桨的螺旋性。滑移网格方法不仅捕捉到了毂涡，还捕捉到了桨叶叶梢处的梢涡。

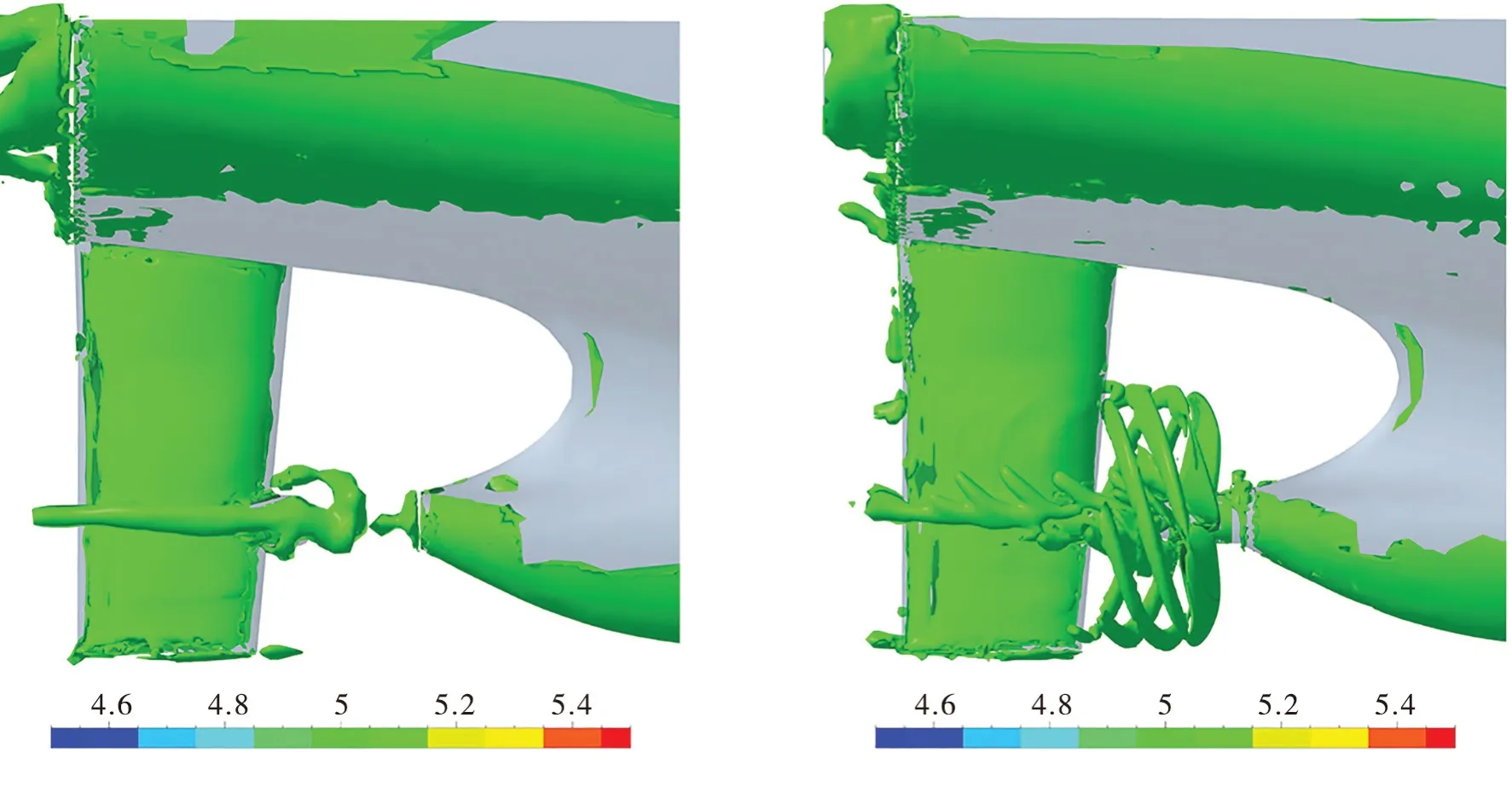
图9 体积力方法（左）与滑移网格方法（右）Q=5等值面的涡结构

为了进一步比较体积力与真实螺旋桨对尾流场的影响，在桨盘面前后0.15处选取截面（如图10所示），截面形状为与螺旋桨同轴、内直径为0.30、外直径为1.00的圆盘。

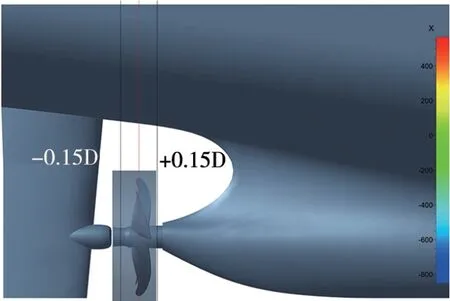
图10 尾流场截面位置

2种方法计算得到的桨前0.15处截面无量纲化轴向、切向和径向速度场如下页图11所示。从船尾向前看，轴向速度V以指向船尾为正，切向速度V以顺时针方向为正，径向速度V以向外为正。体积力方法得到的轴向、切向和径向速度场基本呈对称分布，未体现切向体积力对桨前近桨盘面处水流的作用。滑移网格方法模拟真实螺旋桨的旋转使桨前近桨盘面处水流产生了扭转，导致桨前轴向、切向和径向速度场非对称分布。滑移网格方法桨前径向速度场分布结构与体积力方法类似。

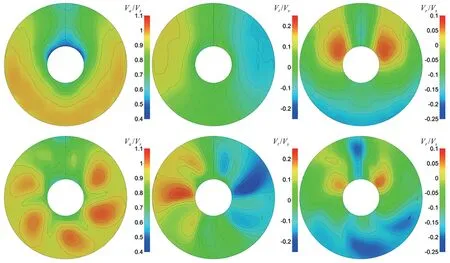
图11 体积力方法（上）与滑移网格方法（下）桨前0.15D处截面无量纲化轴向、切向和径向速度分布

2种方法计算得到的桨后0.15处截面无量纲化轴向、切向和径向速度场如下页图12所示。体积力方法得到的桨后轴向、切向和径向速度场不再呈对称分布，在切向体积力作用下速度场分布呈现出一定偏转。滑移网格方法得到的桨后轴向、切向和径向速度场在螺旋桨旋转作用下也呈非对称分布。两者桨后轴向速度分布结构类似，盘面内径和外径附近轴向速度小，内径与外径之间轴向速度较大，但是体积力方法桨后轴向速度沿周向分布不均匀，而滑移网格方法桨后轴向速度沿周向均匀分布。两者桨后切向速度分布结构也比较相似，盘面左上侧切向速度较大，且两者切向速度较大区域的形状相差不大，而盘面右下侧切向速度由内到外逐渐减小，到外径附近切向速度与螺旋桨旋转方向相反。两者桨后径向速度分布相差较大，主要是因为体积力方法只考虑了轴向力和切向力而未考虑径向力。

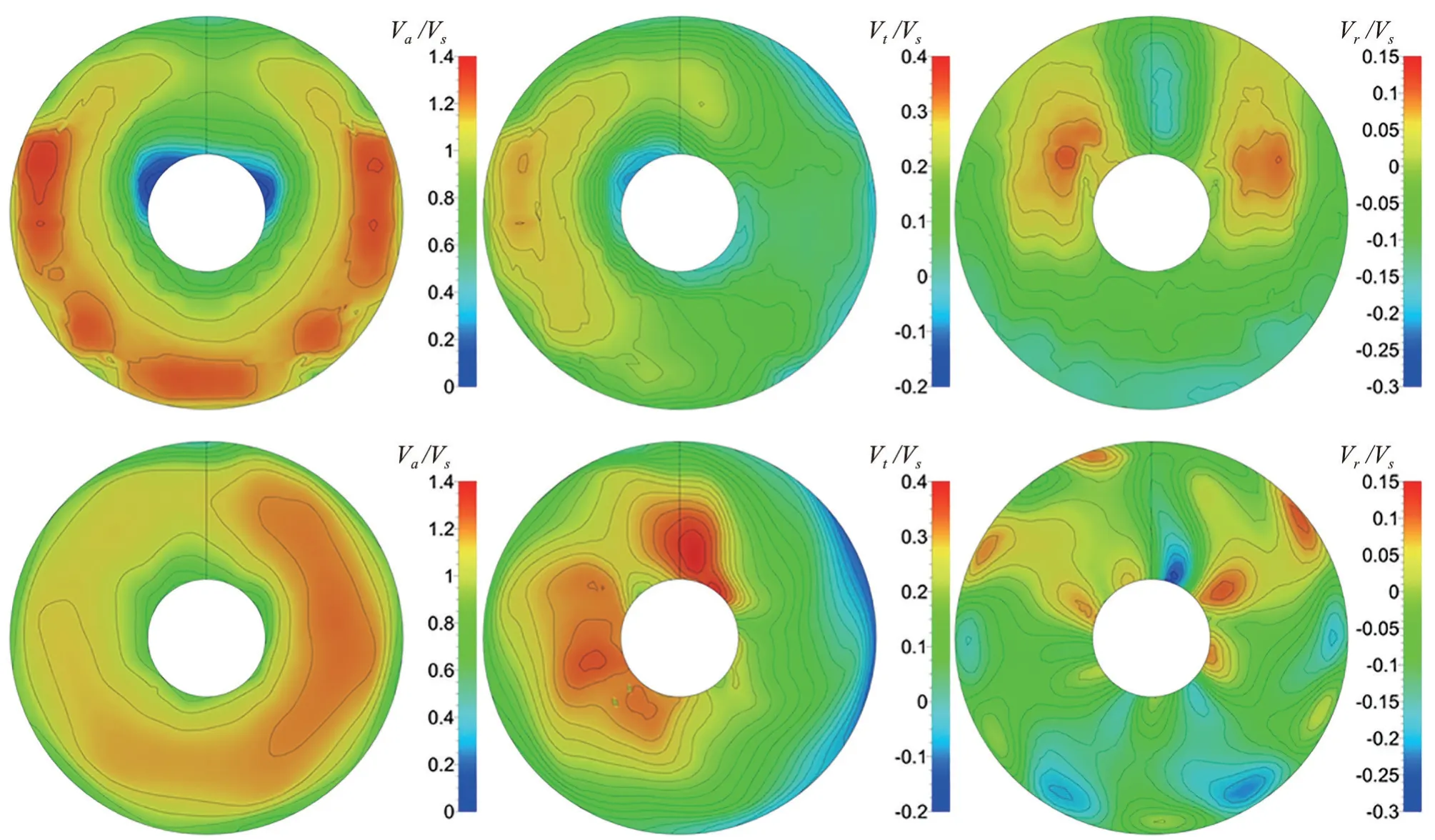
图12 体积力方法（上）与滑移网格方法（下）桨后0.15D处截面无量纲化轴向、切向和径向速度分布

2种方法计算得到的桨前和桨后0.15处截面无量纲化横向(切向、径向)速度矢量分布分别如图13和图14所示。两者桨前横向速度矢量分布差异明显，体积力方法桨前横向速度矢量分布几乎对称，而滑移网格方法的横向速度矢量周向分布不均匀，在桨叶附近横向速度较大，且其盘面上方两侧的小涡比前者更靠近桨毂。两者桨后横向速度矢量分布结构较为相似，由于自航点转速差异，两者横向速度大小存在差异，此外，滑移网格方法的径向流动更为明显。

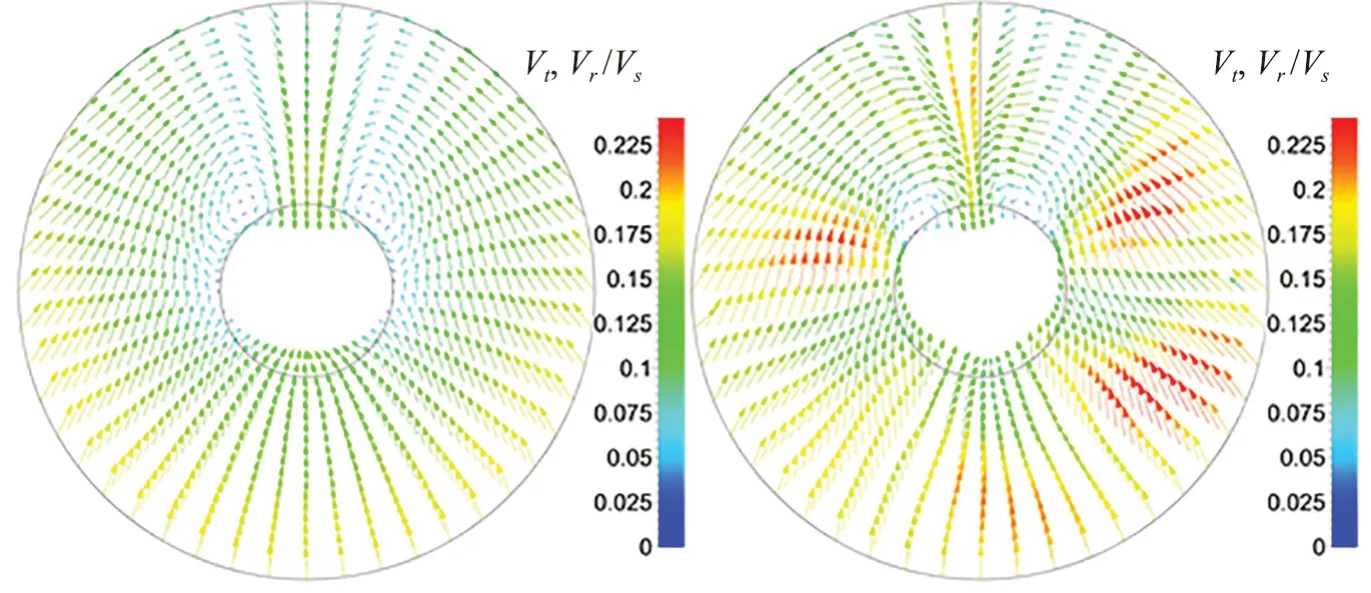
图13 体积力方法（左）与滑移网格方法（右）桨前0.15D处截面无量纲化切向、径向速度矢量分布

图14 体积力方法（左）与滑移网格方法（右）桨后0.15D处截面无量纲化切向、径向速度矢量分布

本文采用体积力方法和滑移网格方法对9 400 TEU集装箱船进行实尺度自航性能数值模拟。通过数值计算方法研究发现，网格划分对计算精度有较大影响，其中船身表面实际平均值在300左右、螺旋桨表面实际平均值在500左右时，计算精度较高；采用激励盘方法时，激励盘厚度选取对计算精度影响较大，建议参考螺旋桨桨叶侧投影轮廓厚度确定；采用滑移网格方法时，动区域大小选取对计算精度影响较大，需避免动区域距离桨叶过近。

6 结 语

体积力方法和滑移网格方法的实船自航性能预报结果与模型试验换算及实船试航结果吻合较好，表明2种方法用于实尺度数值计算预估实船性能时具有较高的可靠性。相对于滑移网格方法，体积力方法由于网格数量更少计算效率更高，但是无法得到螺旋桨相对旋转效率并且额外需要螺旋桨敞水数据。两者对螺旋桨模拟方式不同造成尾流场的差异，对于桨前流动，两者主要差异在于轴向和切向流动，体积力方法未能体现螺旋桨旋转效应；而对于桨后流动，两者主要差异在于径向流动，体积力方法未考虑径向力的作用。

本文进行实尺度自航性能数值模拟时，未考虑船体表面粗糙度和空气阻力的影响，后续需进一步研究。