解答平面向量最值问题的常用策略
2022-10-23陈立云
高中数理化 2022年17期
陈立云
(福建省莆田市莆田第十一中学)
作为连接高中数学代数与几何图形的枢纽,平面向量发挥着重要的作用.它是高考数学考查频率较高的内容,其中平面向量的最值问题尤为常见,短小精悍的问题往往蕴含着“数”与“形”的深层意义,解答策略和思路灵活多变,因此需要学生熟练掌握求解平面向量最值问题的常用策略.本文结合具体例题,分析不同的解题策略的应用思路与解题步骤.
1 借助坐标运算求解
借助坐标运算求解平面向量最值问题的关键在于建立平面直角坐标系,利用坐标运算建立函数解析式,再根据函数定义域求对应的最值.运用坐标运算策略解题时,要先建立合适的平面直角坐标系,对未知动点进行假设,再结合问题所给条件,将所求的向量运用坐标表示,并进行运算得到相关函数解析式,最后在函数定义域内,求出函数对应的最值.


图1

解 建立如图2 所示的平面直角坐标系,则B(2,0),C(2,1),D(0,1).设Q(x,1),P(2,y)(0≤x≤2,0≤y≤1).

图2


图3

解 如图4所示,以点A为原点,边AB所在直线为x轴,边AD所在直线为y轴建立平面直角坐标系,设点
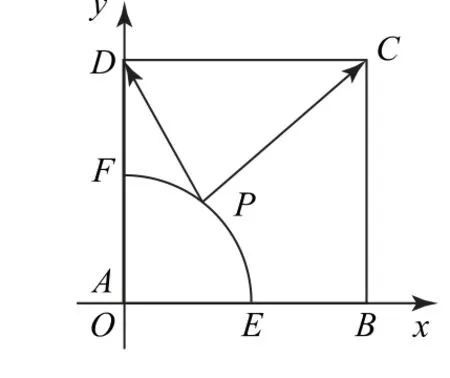
图4

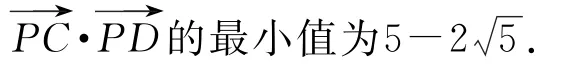
2 构造几何图形求解
构造几何图形策略解答平面向量最值问题,主要是根据问题中的已知条件构造三角形、圆等几何图形,赋予问题具体的几何意义,运用几何性质和定义解答.构造几何图形求解这一类问题,常见的解题步骤为分析题意,根据所给条件构造对应的几何图形,使问题具有具体的几何意义,再探索最值对应的几何图形情况,运用几何性质或定理求出最值.


图5

图6



图7
平面向量最值问题灵活多变,根据内容形式的不同可以采取不同的解题策略.坐标运算、构造几何图形等都是解答平面向量最值问题较为常见的解题策略,也都是学生需要熟练掌握的策略.合理运用这些策略,能使较为复杂抽象的问题简单化、直观化,从而提高解题效率.
