求解平面向量问题的常用方法

王 龙

(陕西省渭南市瑞泉中学)

平面向量是联系高中数学几何知识与代数知识独特且关键的桥梁,因此平面向量问题是高考数学必不可少的考题.解答平面向量问题有很多种方法,其中投影法、基底法、坐标法最为常用,是学生必须掌握的解题方法.通过具体例题,分别介绍这三种方法对应的解题思路与具体应用过程,以期加深读者对于这些方法的理解,并能熟练运用这些方法高效、正确地求解问题.

1 投影法

投影法是求解平面向量问题的常用方法,主要是根据数量积公式a·b＝|a|·|b|cosθ(其中θ＝〈a,b〉)对模长和角度进行分析,进而对问题做出解答.运用该方法解答平面向量问题的一般思路为:结合已知平面几何关系,找到与问题所求有关的向量和对应投影向量,再凭借向量数量积公式的几何定义,对未知的模长或角度进行推理分析,通过运算得到最终答案.

图1

2 基底法

基底法具体是指选择一组已知向量作为基底向量,根据所给条件将问题所求等价转化为只含基底向量的表达式,进而通过运算求出问题所求的对应值大小.运用基底法求解这一类问题时,一般解题思路为:根据问题所给条件,选择一组向量作为基底向量,运用平面向量矢量法则,将问题所求转化为用基底向量表示的解析式,代入基底向量具体值,即可得到问题的最终答案.

图2

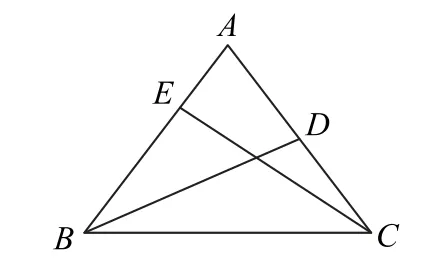
图3

3 坐标法

作为解答平面向量问题的常用方法,坐标法的运用十分广泛,具体是指通过几何关系建立平面直角坐标系将所求问题的向量坐标化,利用坐标运算对问题做出解答.该方法在解题中的一般思路为根据已知条件建立平面直角坐标系,求出已知点的坐标,对未知点进行假设,通过平面向量的坐标运算,对问题做出分析与解答.

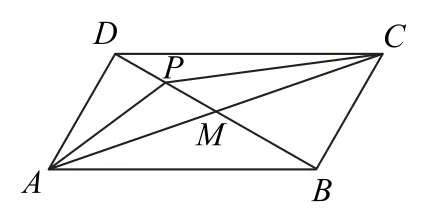
图4

图5

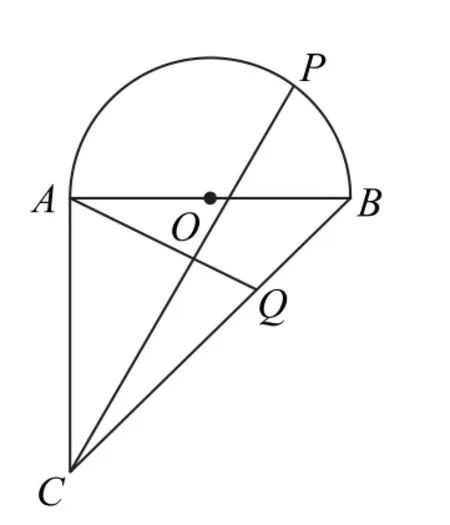
图6

图7

上述三种不同的解题方法都是解答平面向量问题常见的方法,投影法在于灵活运用数量积公式进行投影的转化,基底法的运用关键在于选择合适的基底向量,坐标法则通过向量的坐标运算进行求解.每一种方法都有与之对应的解题思路,在运用这些方法时,应多思考、多实践、多总结.只有结合自己的理解使其成为属于自己的解题方法,才能使这类平面向量问题迎刃而解.