基于主成分与回归分析的弹药消耗预计方法*

史宪铭，李 康，刘月河，姜广胜，杜 凯

（陆军工程大学石家庄校区，石家庄 050003）

0 引言

弹药是战斗力的物质基础，打仗没有弹药毫无办法。国内相关学者在弹药消耗预测方面做了大量研究，对有效保障弹药需求具有十分重要的意义。随着科技的发展，武器的作战性能和目标的防护性能也得到了一定发展，导致作战过程中弹药消耗影响因素也发生变化，对弹药保障工作带来了严峻挑战。

目前，在分析弹药消耗影响因素研究中，龚传信等构建了面向目标的弹药消耗的影响因素体系，运用DEMATEL 方法定量分析了面向目标的弹药消耗影响因素，其充分利用了专家的经验知识，找出了影响面目标的弹药需求关键因素。李建华等基于模糊逻辑理论建立了弹药消耗预计模型，定量分析了弹药消耗影响因素，其通过建立弹药消耗影响因素的隶属度函数，综合了弹药消耗诸多因素。赵志宁等提出一种基于可拓优度的联合火力打击陆军弹药消耗预测方案评估模型，通过建立因素重要程度模糊评判矩阵，深入分析了联合火力打击陆军弹药消耗影响因素。

上述弹药消耗预测方法多利用专家打分、模糊评判等方法分析弹药消耗影响因素，对影响因素的研究具有一定的主观性和不准确性。主成分分析是一种多元统计分析方法，可以消除弹药消耗影响因素彼此的相关影响，减少评价指标选择的工作量。回归分析可以准确地计量各个弹药消耗影响因素之间的相关程度与回归拟合程度的高低，提高预测方程式的效果。因此，本文采用主成分分析法确定某装甲武器弹药消耗影响因素主成分，并对其进行了回归分析，预测弹药消耗量。

1 基于主成分的弹药消耗影响因素分析

1.1 主成分分析基本模型

假定有n 个样本，每个样本有p 个指标变量，数据矩阵可以表示为：

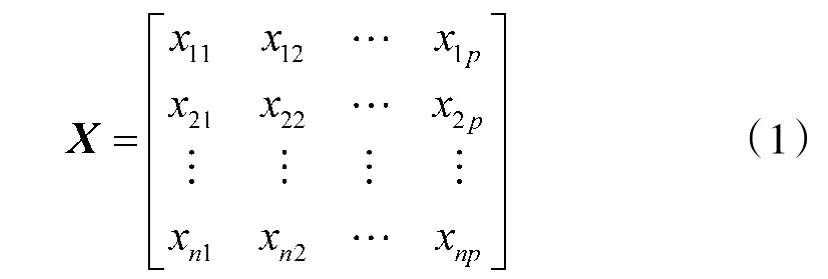
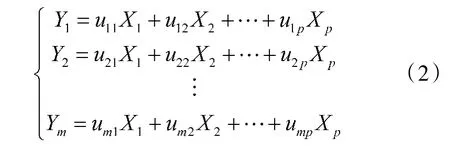
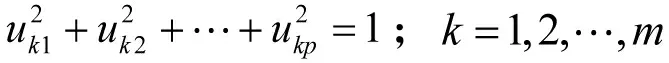
由于对任意变量可作上述线性变换，得到的综合变量Y 的统计特性也各不相同，为达到最好效果，系数u有如下约束：

1.2 主成分分析计算步骤

1）计算相关系数矩阵

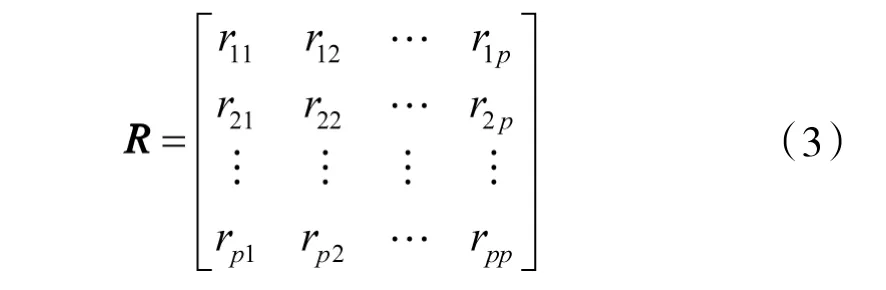
式中，r为原变量x和x之间的相关系数，计算公式为：

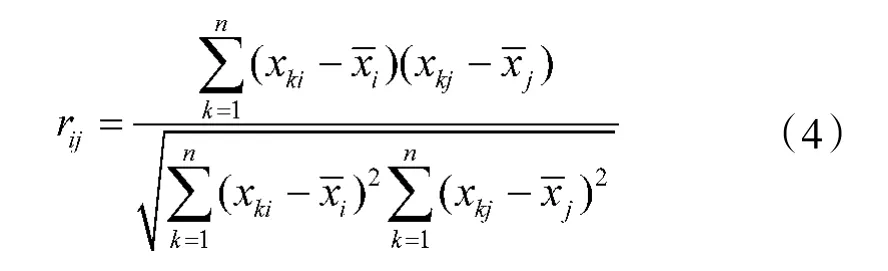
2）计算特征值

特征方程为：

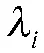
3）计算主成分贡献率与累计贡献率

主成分Y的贡献率z为：

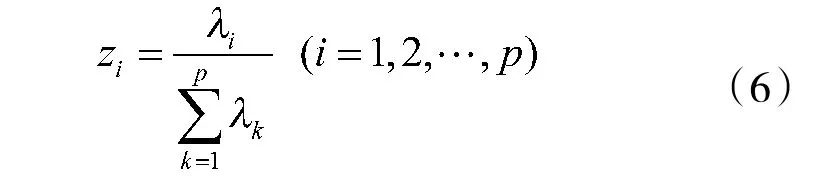
累计贡献率为：

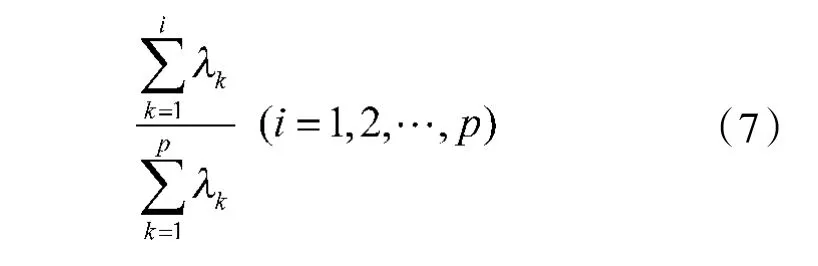
4）计算主成分载荷

主成分载荷计算公式为：

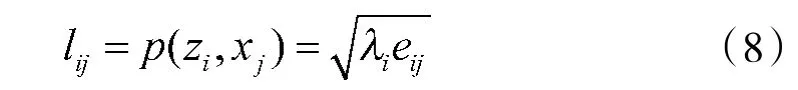
得到各主成分载荷后可进一步计算各主成分的得分。

1.3 基于主成分的弹药消耗影响因素分析

由于弹药消耗受到多重因素的影响，预计弹药消耗是一个复杂的工作，需要先对弹药消耗影响因素进行分析。从宏观角度讲，作战样式、作战规模、作战强度等都对弹药消耗产生影响。本文立足弹药-目标匹配的角度，以确定的某装甲武器为研究对象，面向点目标，不涉及宏观角度下的弹药消耗影响因素，即在弹药、目标以及毁伤程度确定的情况下考虑相关因素。随着科技的进步，武器平台的移动速度和目标的防护程度越来越影响弹药的消耗，因此，本文选取武器与目标的距离、武器平台的移动速度、目标的移动速度、目标规模、目标的防护程度和环境影响系数6 种弹药消耗影响因素。

基于主成分的弹药消耗影响因素如图1 所示，分析步骤具体如下：

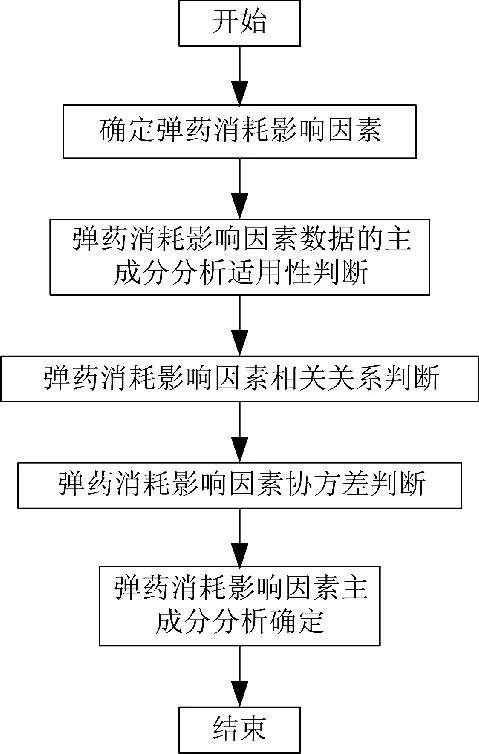
图1 基于主成分的弹药消耗影响因素分析步骤

1）选取相应的弹药消耗影响因素，计算KMO（kaiser-meyer-olkin，表示检验统计量）等指标，比较变量之间的相关性，判断数据是否适合主成分分析。

2）计算相关系数矩阵，分析弹药消耗影响因素之间的相关关系。

3）计算协方差矩阵，分析各弹药消耗影响因素协方差。

4）通过前面的分析确定弹药消耗影响因素的主成分。

2 弹药消耗量回归分析方法

对弹药消耗影响因素进行主成分分析后，得到了降维后的变量，消除了弹药消耗各影响因素之间的相关关系，利用少数影响因素代替多个影响因素，同时又基本涵盖原始弹药消耗影响因素的作用。在实际弹药消耗预计中，根据已有的数据，难以用一个精确的函数将变量联系在一起，进而用回归模型对弹药消耗量进行回归分析。

2.1 弹药消耗量多元线性回归分析

所谓回归分析方法，即利用统计方法建立因变量和自变量的关系，根据提供的自变量，研究因变量的变化，可以用于预计分析。线性回归分为一元线性回归和多元线性回归，以自变量的数量区分。本文中弹药消耗影响因素有多种，故选取多元线性回归。

视弹药消耗量为因变量y，各弹药消耗影响因素为自变量x，其中（i=1，2，…，n），可建立多元线性回归方程：

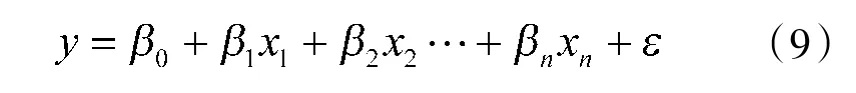
其中，β 为回归系数；ε 为误差。求出回归方程后，需要对方程进行显著性检验，观察弹药消耗量与影响因素是否符合多元线性模型。

通过最小二乘法可以获得多元线性回归方程的参数，即采用最小误差平方和，公式如下：

式（10）即求一组β 使得Q（β）达到最小值，采用普通最小二乘法：

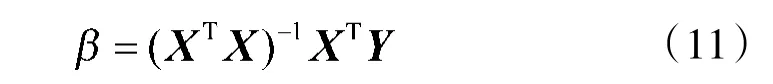
式中，X 为自变量矩阵；Y 为因变量矩阵。

2.2 弹药消耗量多元非线性回归分析

非线性关系，包括3 类，1）可以通过变量替换转化为线性关系；2）自变量和因变量之间关系函数式不确定；3）自变量和因变量之间关系函数式可以确定，但参数未知，且不可转化为线性关系。

一般多元非线性回归模型公式为：

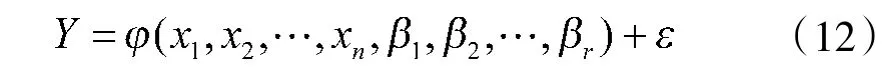
给定一组弹药消耗预计的弹药消耗量与各影响因素的观测值后，式（12）可改写为：

其中，β 为回归系数；x为弹药消耗影响因素，根据弹药消耗影响因素的个数可以确定非线性函数的维数；ε为随机误差项，接受独立同分布假定条件，即：

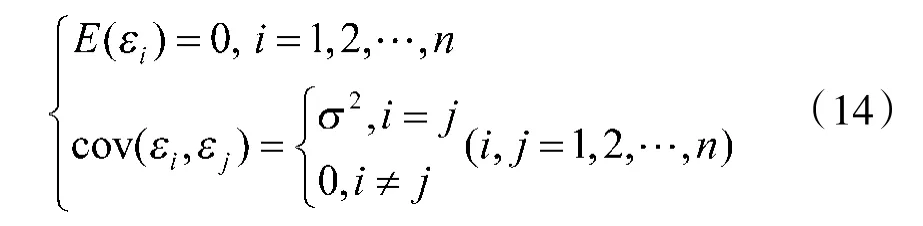
对于非线性回归模型，仍使用最小二乘法估计参数，即：

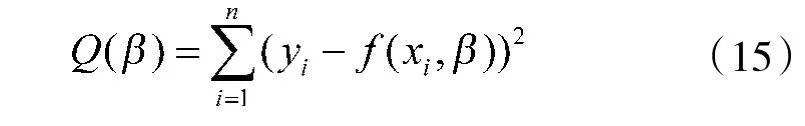
3 示例分析

本文以某装甲武器为例，研究对点目标的弹药需求预计。根据1.3 节中弹药消耗影响因素分析，选取武器与目标的距离、武器平台的移动速度、目标的移动速度、目标规模、目标的防护程度和环境影响系数进行主成分分析，分别对应x，x，x，x，x，x6 个变量。弹药消耗影响因素数据归一化处理后如表1 所示。

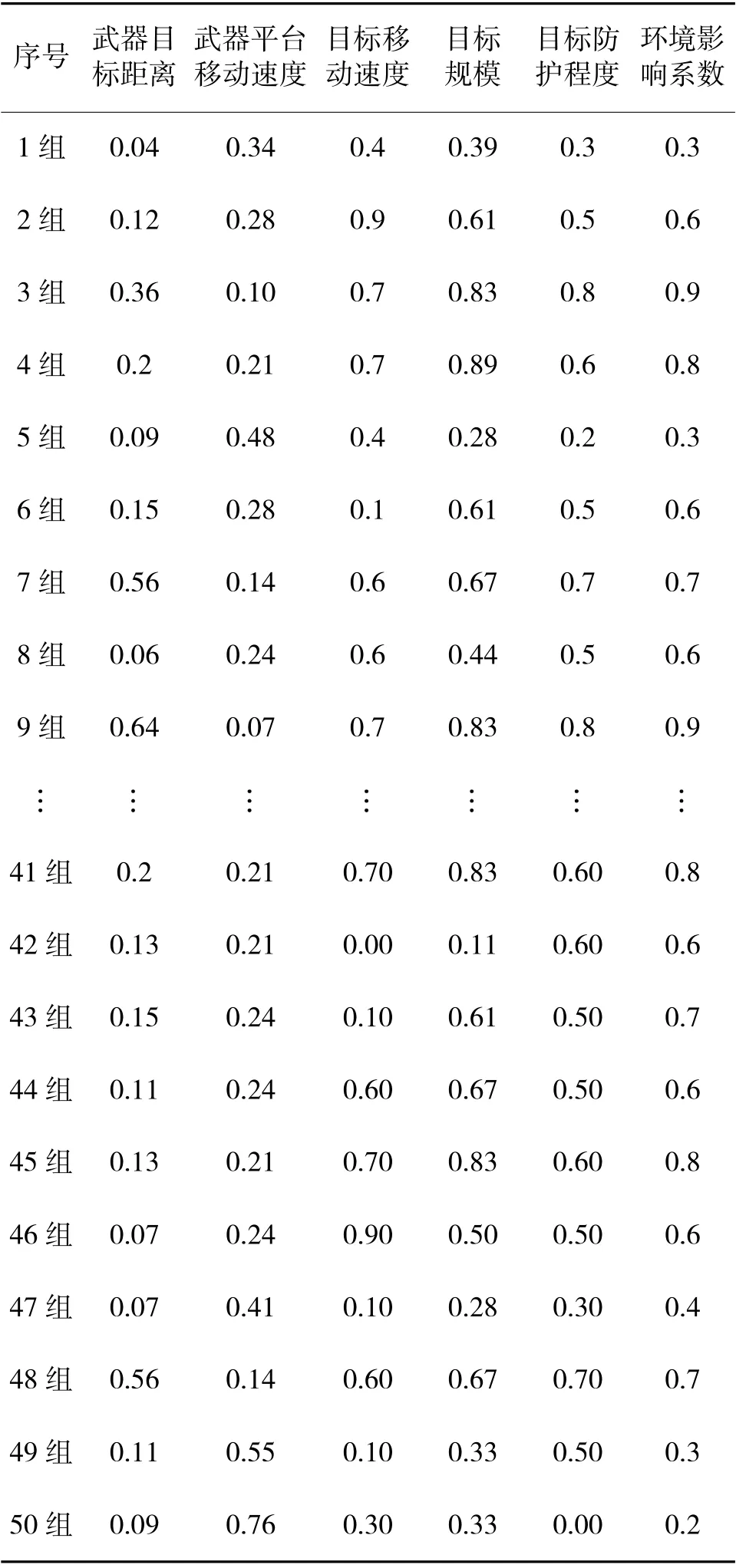
表1 弹药消耗影响因素数据

对选取的6 个弹药消耗影响因素指标首先进行KMO 检验，判断其是否适合主成分分析，KMO 值计算结果如表2 所示。一般来说，KMO 值在0.8 以上适合做主成分分析，在实证分析中能达到0.6 以上，就认为可以进行主成分分析。据表2 中数据可以看出弹药消耗影响因素可以进行主成分分析。主成分分析结果如下页表3 所示，第2 列代表特征值。具有95%置信度渐进置信区间的碎石图如图2所示。分析表中数据可以看出前两个主成分累计贡献率达到84%，且根据特征值大于1 的主成分选定条件，选择前两个主成分可以很好解释原始变量。图3 是主成分分析后的得分图，描述了各组数据得分散点图，图4 为主成分分析所得载荷图，可以直观看出各弹药消耗影响因素对主成分影响的大小。

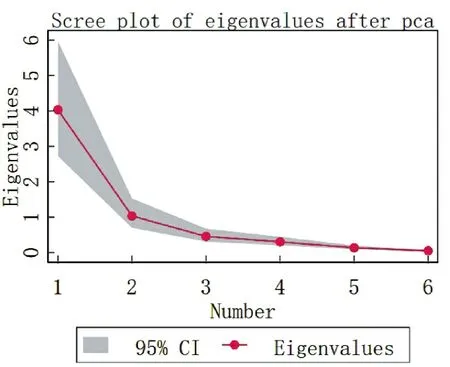
图2 特征值95%置信区间碎石图

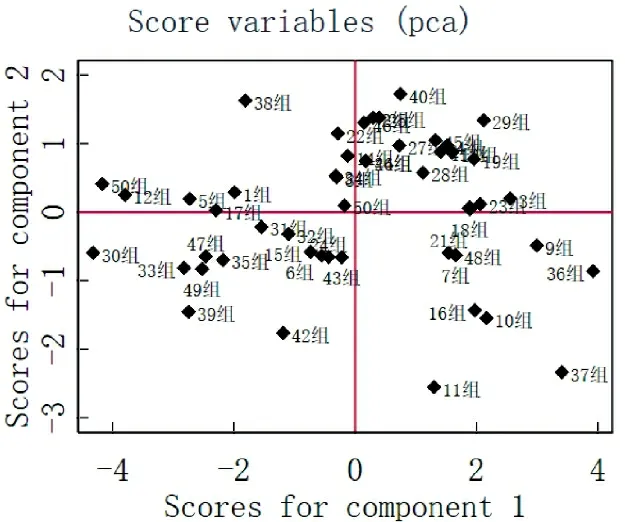
图3 主成分分析的得分图

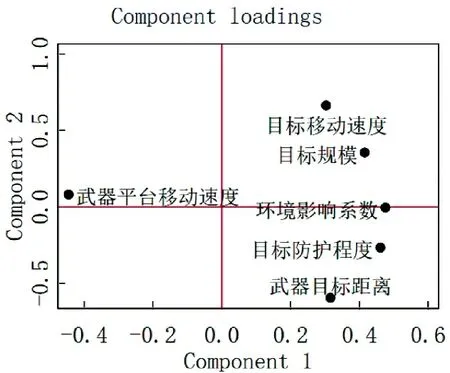
图4 主成分分析因子载荷图

表2 弹药消耗影响因素KMO 值

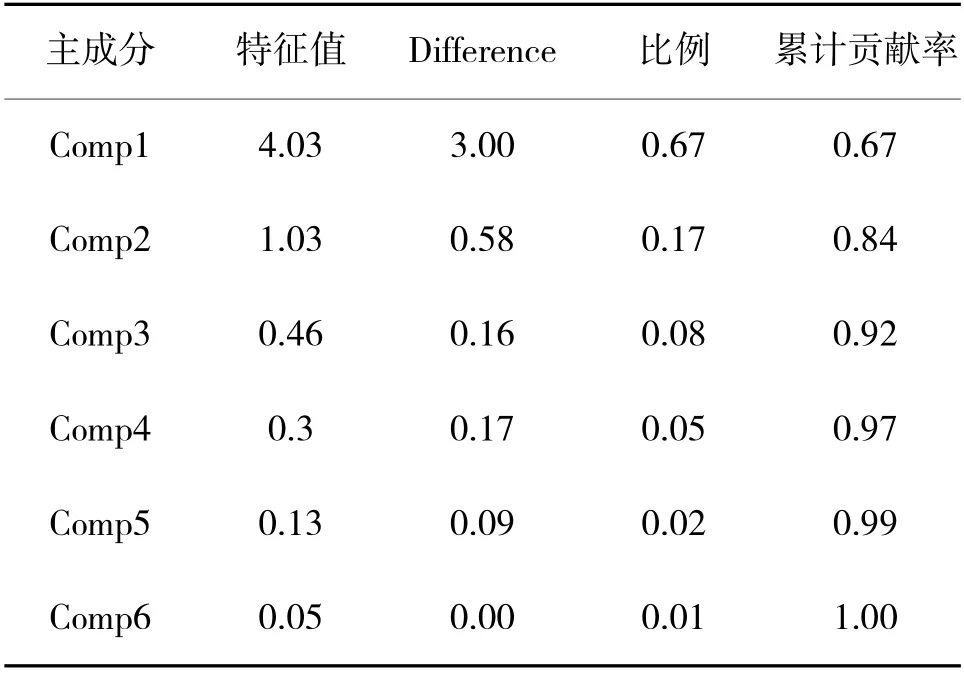
表3 弹药消耗影响因素主成分分析结果

通过对载荷矩阵进行旋转，得到主成分对应的特征向量如表4 所示。

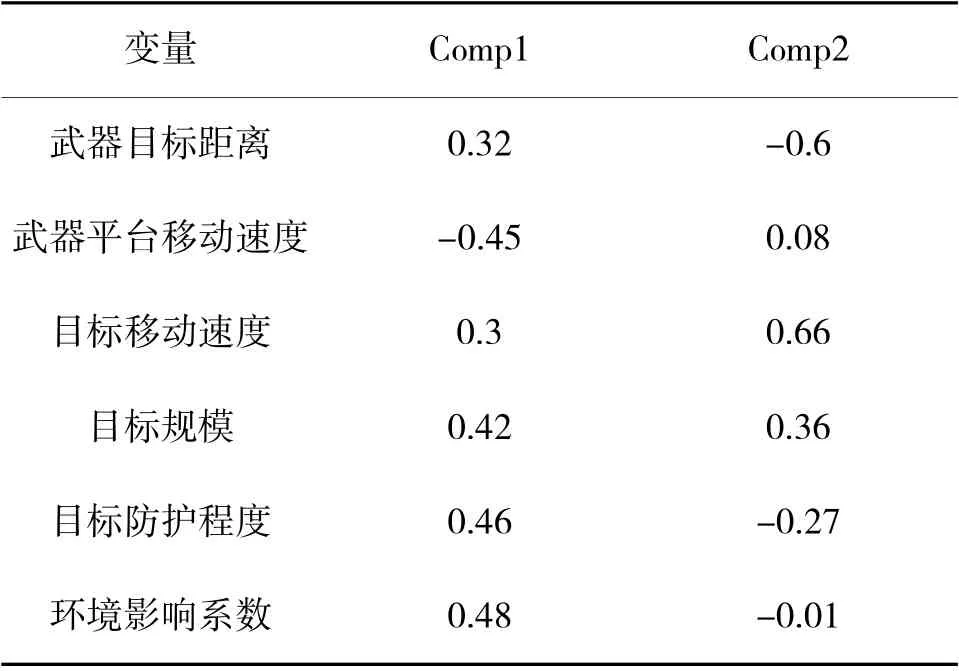
表4 第一、二主成分特征向量

则两个主成分的表达式为：

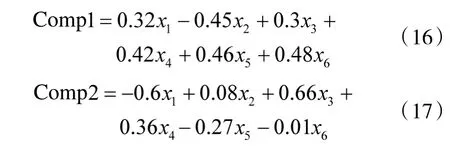
以主成分Comp1、Comp2 为自变量，弹药消耗y量为因变量，进行多元线性回归分析后结果如表5所示，表明解释变量均显著，可得线性回归方程为：

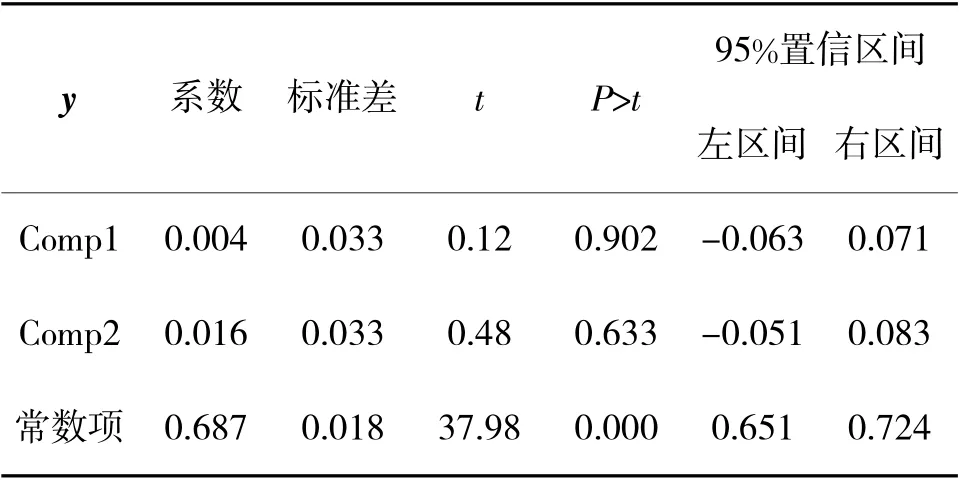
表5 线性回归结果

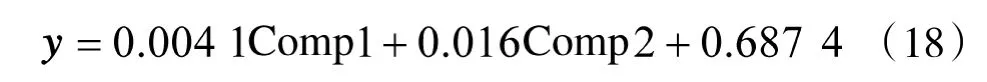
以主成分Comp1、Comp2 为自变量，弹药消耗量y（表示弹药消耗基数）为因变量，进行多元非线性回归分析后结果如表6 所示，z，z，z，z，z分别表示Comp1，Comp2，Comp1，Comp2，Comp1Comp2，可以看出解释变量均显著，可得非线性回归方程为：

表6 非线性回归结果

选取3 组数据检验线性回归和非线性回归方程预测弹药消耗量的效果，结果如下页表7 所示。由表5～表7 可以看出，对弹药消耗影响因素进行主成分分析后，以得到的主成分作为自变量进行回归分析，其中非线性回归方程的估计标准差和误差更低，可以用来预测弹药消耗。

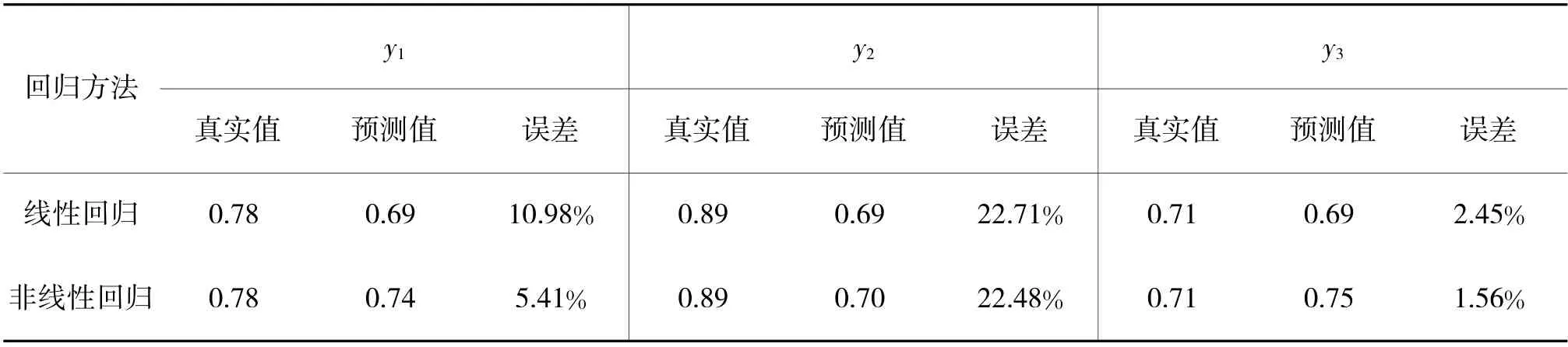
表7 回归预测结果对比

4 结论

论文采用主成分分析方法分析弹药消耗影响因素，以获取的主成分作为自变量，分别用线性回归模型和非线性回归模型，预测了不同影响因素条件下的弹药消耗量，结果表明非线性模型更适于弹药消耗预测。战场情况复杂多变，影响弹药消耗的因素众多，影响因素的选取和弹药消耗数据的收集是下一步研究的难点。