互耦误差下环形共形阵列多参数联合估计*
2022-10-23侯文林谢吉鹏
胡 月,高 猛,侯文林,谢吉鹏
(空军通信士官学校,辽宁 大连 116600)
0 引言
共形阵列天线是将天线阵元附着在共形载体表面,阵列形状随着载体表面的变化而变化的天线阵列,能够充分利用载体表面,不影响飞行器动力性能,相比常规天线具有无法比拟的优势。利用战机上的共形阵列天线对信源来波方向的无源探测具有隐蔽性强的特点,可极大地提升战机的生存能力,使用的算法主要为高分空间谱估计算法,这些算法实现的前提是阵列流型精确已知。但在实际应用中,阵元接收信号的同时也在向外辐射干扰,这就是互耦效应。受共形载体的散射效应等因素的影响,共形阵列中的互耦效应更为严重。互耦效应导致阵列流型出现偏差,信源方位估计偏差增大、甚至失效。受共形载体曲率的影响,各阵元单元方向图函数各不相同,进行DOA 估计需要同时考虑信源方位、极化参数和互耦系数3 种参数,经典阵列中的互耦误差校正算法无法直接移植到共形阵列中。文献[8]提出了共形阵列互耦误差校正的辅助阵元法,只需3 个精确校正的辅助阵元,即可实现互耦、通道幅相等多种误差的校正,且适用于多种共形载体,但要求辅助阵元精确已知。实际应用中,精确校正的辅助阵元往往难以构造。文献[9]提出了圆台共形阵列互耦误差校正算法,但未涉及信源极化参数对校正算法的影响,未考虑共形阵列的遮蔽效应,且在参数迭代求解中易得到局部最优解,而不是全局最优解。目前国内在球面共形阵列误差校正方面的研究还较少。故探讨无需辅助阵元、多参数相互耦合情况下的球面共形阵列互耦误差校正算法具有重要意义。
本文针对球面环形共形阵列互耦误差校正问题展开,建立了球面环形共形阵列互耦误差模型;利用天线单元方向图正交分量的差异、互耦矩阵的特点,实现了信源方位、极化和互耦系数的分离;在此基础上利用“秩损理论”,通过二维参数搜索得到信源方位的估计值,进而估计出信源极化参数和互耦系数,无需参数配对;最后分析讨论了算法参数估计的统计一致性与有效性,推导了参数估计的极限性能。
1 球面环形共形阵列天线互耦误差模型
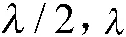
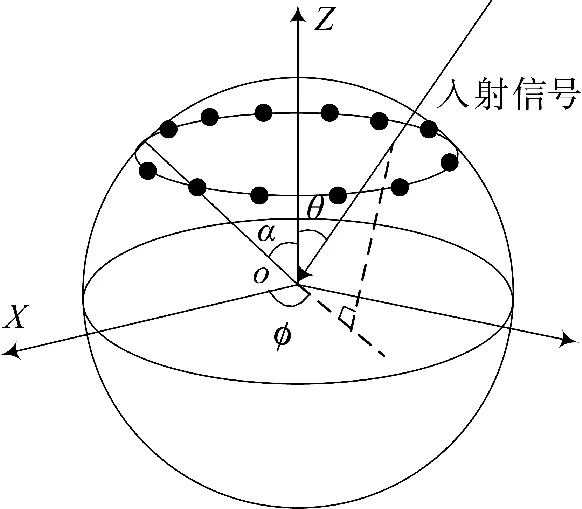
图1 球面环形共形阵列天线

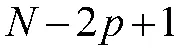

式中,为理想的导向矢量,其表达式为:
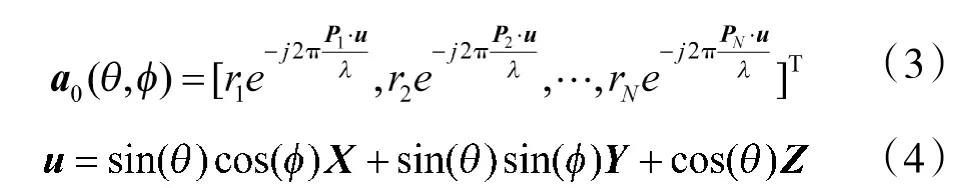
其中,j 为虚数单位;P为在全局坐标系中第i 个阵元的位置矢量;u 为入射信号的方向矢量;r为单位强度入射信号在第i 个阵元上的响应,可表示为:
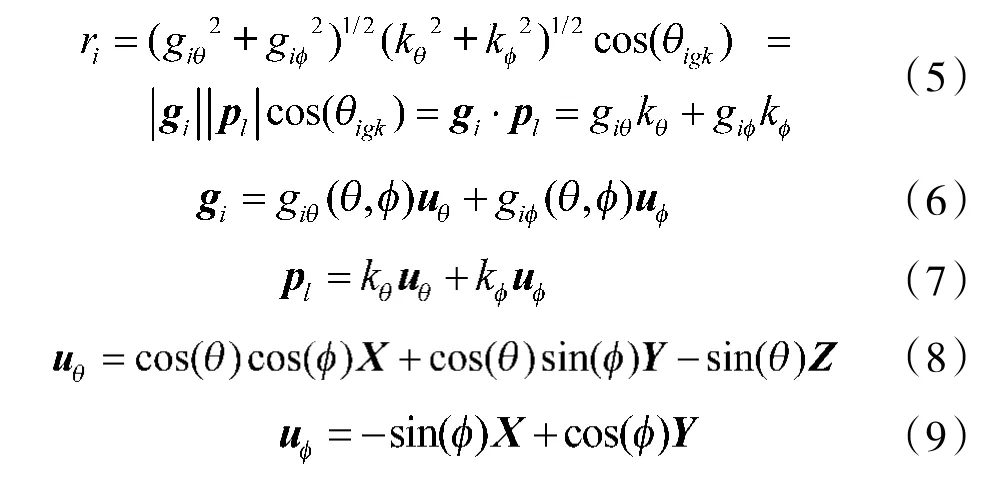
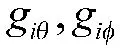
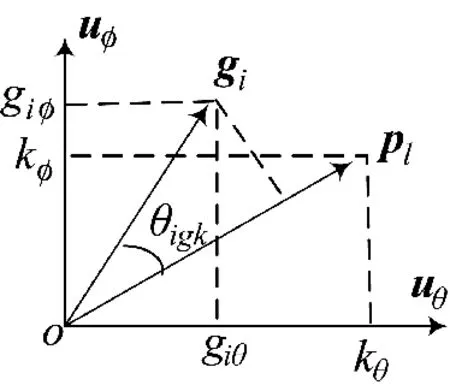
图2 阵元在全局坐标系中对入射信号的响应
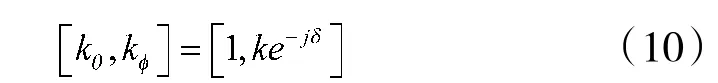
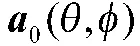
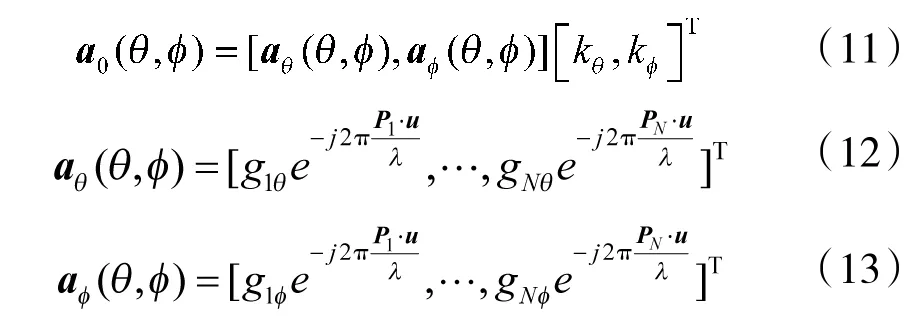
各阵元单元方向图函数g是由局部坐标系中参数表示的,但在应用中需要将局部坐标系中的参数转换为全局坐标系中的参数,以便各方向图函数统一计算,所以共形天线建模时必须完成参数从局部坐标系到全局坐标系的旋转变换。
假设空间有处有M 个同频窄带独立信源,阵列接收快拍数据可表示为:
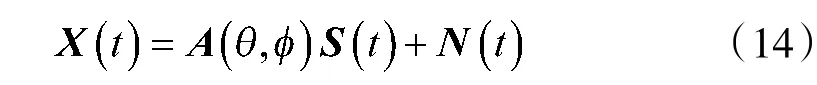
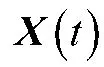
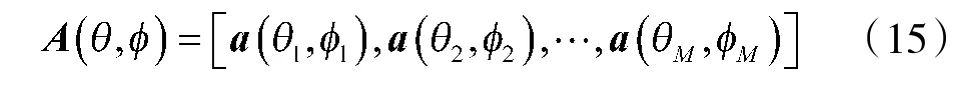
2 互耦误差条件下的多参数联合估计算法
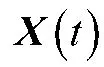
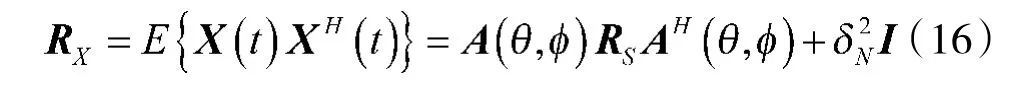
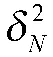
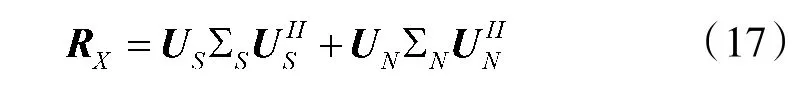
其中,U为M 个大特征值对应的特征矢量构成的矩阵,是信号子空间的基;U为(N-M)个小特征值对应的特征矢量构成的矩阵,是噪声子空间的基。由子空间原理有:
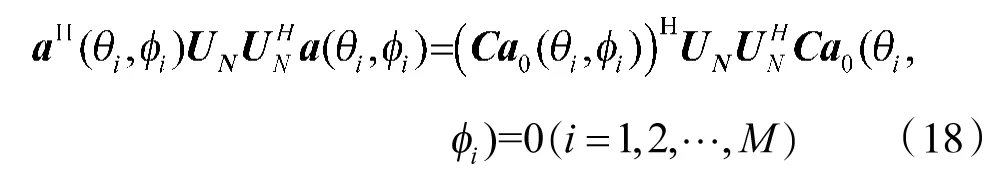
将式(10)、式(11)代入式(18)可得:
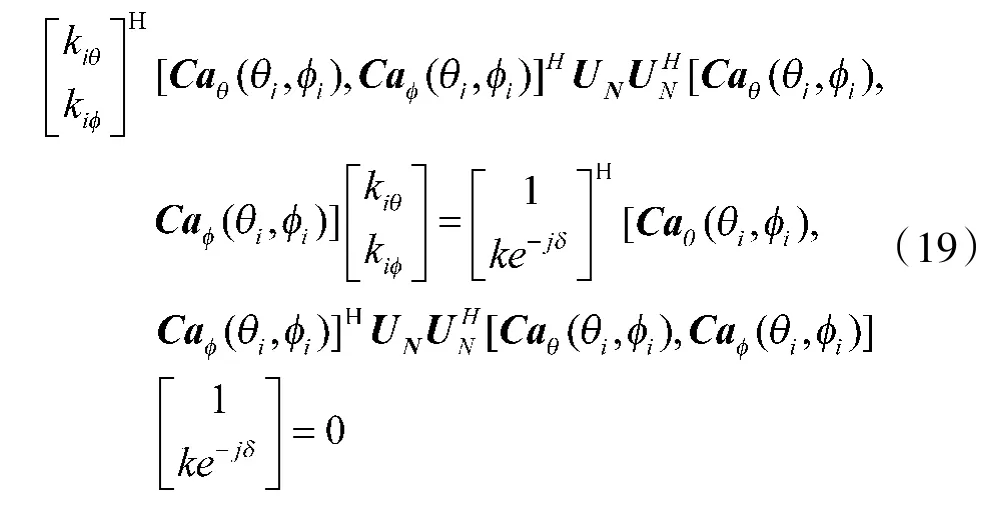
互耦矩阵C 为条带对称toeplitz 矩阵,故有:

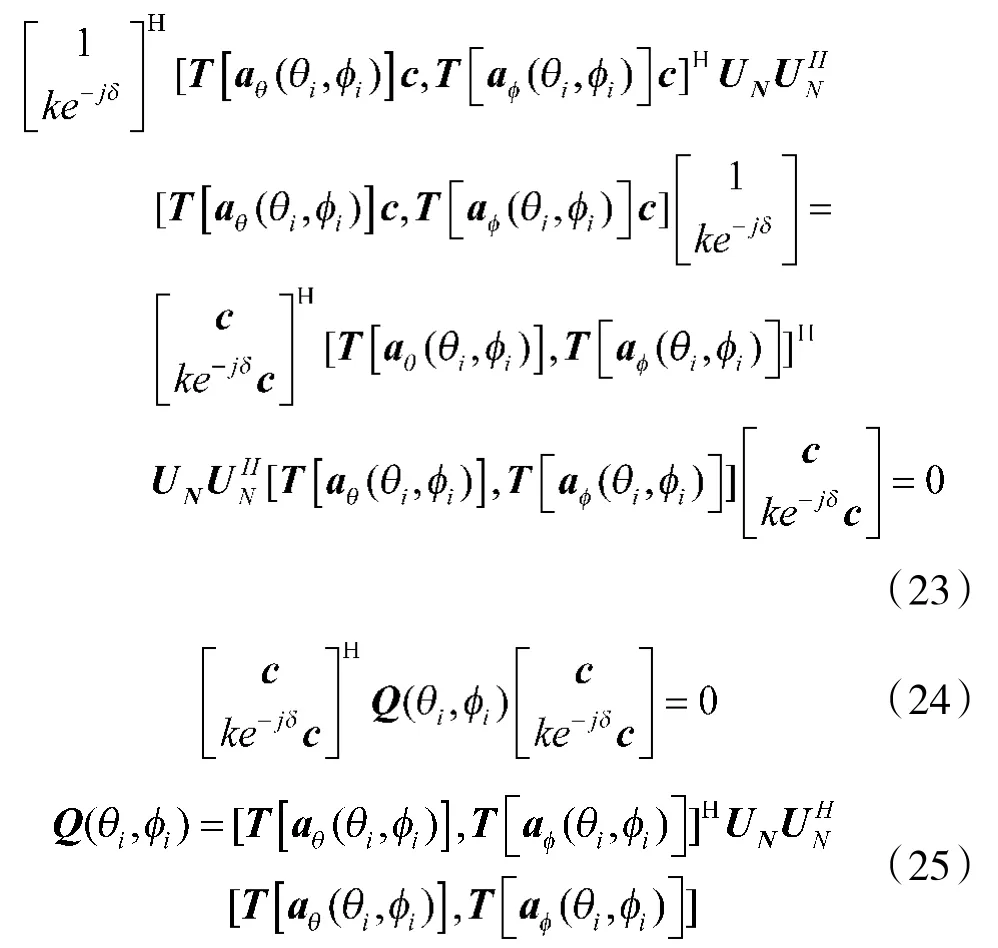
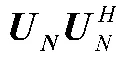
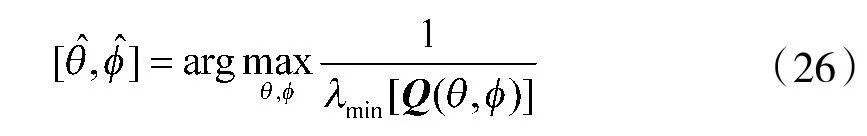
或:
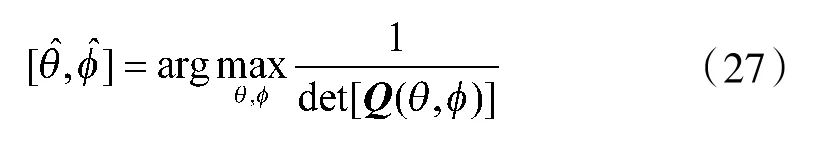
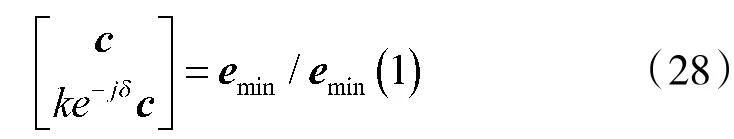
所以:
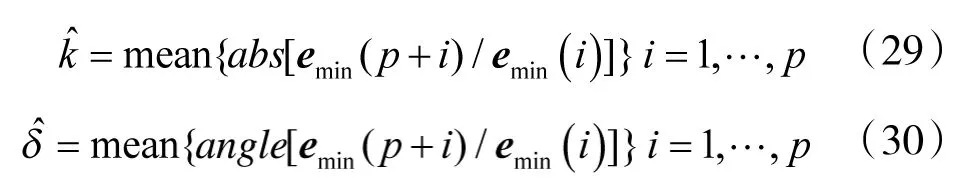

综上所述,本文算法流程如下:
1)由式(14)和式(16)得到阵列接收的快拍数据X(t)的协方差矩阵R,对其特征分解得到噪声子空间U;
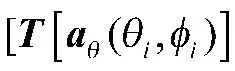
3)对式(26)或式(27)进行谱峰搜索,找出极大值点对应的角度即为信源方位;
4)由式(28)~式(30)得到互耦系数和极化参数的估计值。
3 算法性能分析
3.1 参数估计统计一致性的证明
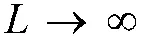
当阵列快拍数

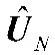


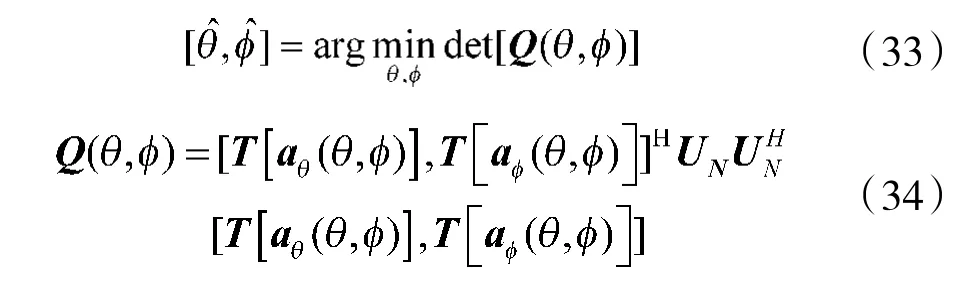
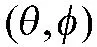
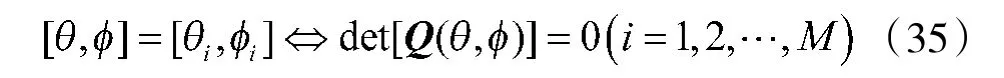
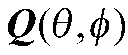
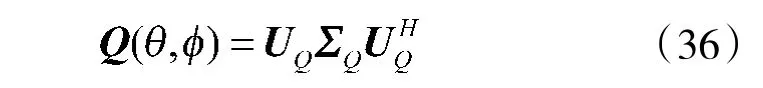
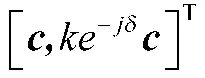
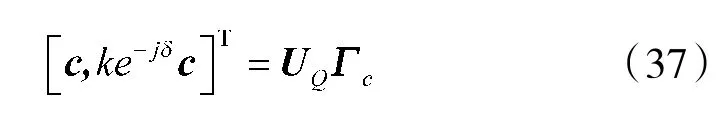
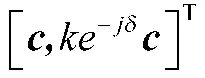
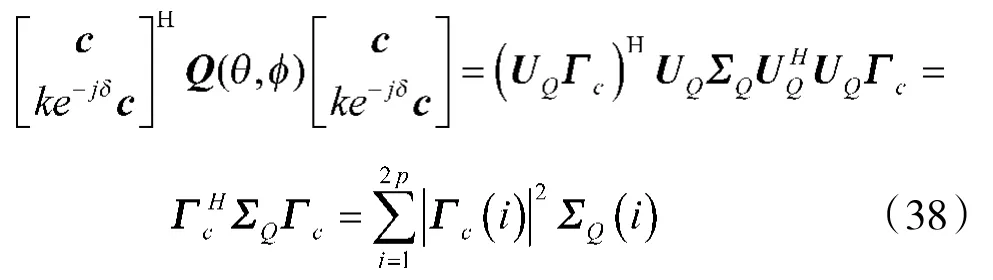

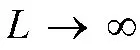
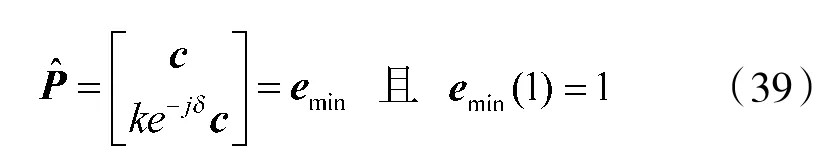
要证明互耦系数和信源极化参数估计的统计一致性,只需证明:
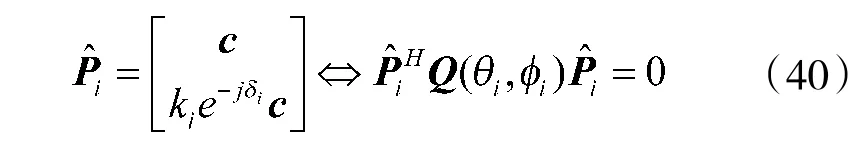
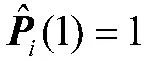
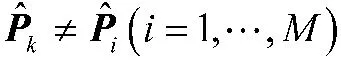
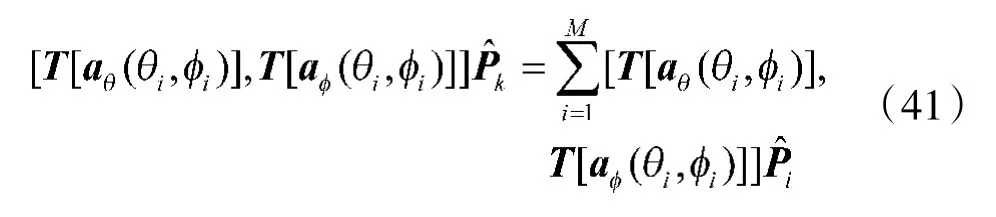
式(41)与存在互耦误差的阵列导向矢量满足无秩M-1 模糊时相矛盾,故假设错误,从而证明了互耦系数和信源极化参数估计的统计一致性。
3.2 参数估计的CRB
参数估计的CRB(cramer-rao bound)给出了参数无偏估计方差的下界。下面将计算信源方位、极化和互耦系数联合估计的CRB 表达式。
为了简化推导过程,将噪声方差归一化为1,设信源的相关矩阵R已知。阵列接收快拍数据协方差矩阵R中包含4M+2p-2 个未知实参数,即2M 个信源方位参数、2M 个信源极化参数和2p-2 个互耦系数,可表示为:
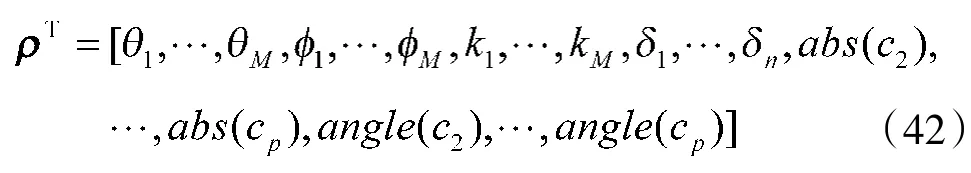
信源方位、极化和互耦系数联合估计的CRB 可表示为:

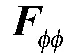
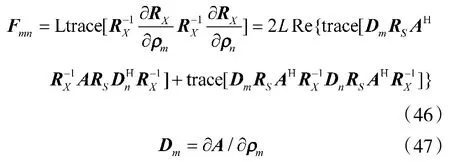
式中,trace(·)表示取矩阵(·)的迹;矩阵A 的表达式如式(15)所示。
本文算法需要进行二维搜索,每一个搜索点需计算式(25),其计算量为2p(N-M)(N+p)次复乘法,还需计算式(26)的行列式,其计算量为p(p-1),故本文算法的计算量为n(2p(N-M)(N+p)+p(p-1)),n 为每一维搜索总点数。
4 仿真分析
以下对本文算法进行MATLAB 仿真验证。若信源方位估计值与真实小于1°,则认为仿真有效。成功概率的定义为:仿真有效次数与仿真总次数的比值。估计偏差定义为:有效仿真中,信源估计值与真值之差的绝对值。估计标准差定义为:有效仿真中,信源估计值与真值之差的均方值开方。
4.1 仿真条件
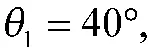
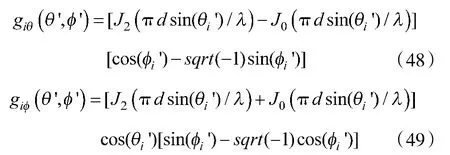
当θ'>π/2 时:

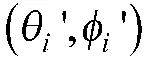
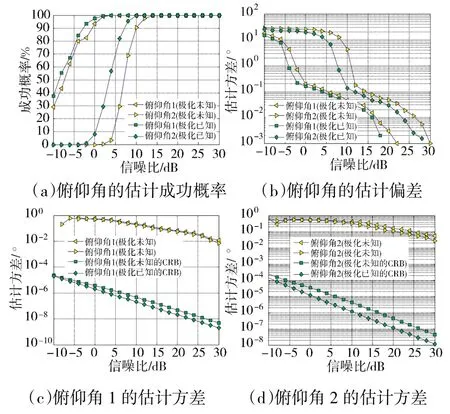
图3 俯仰角的估计效果曲线
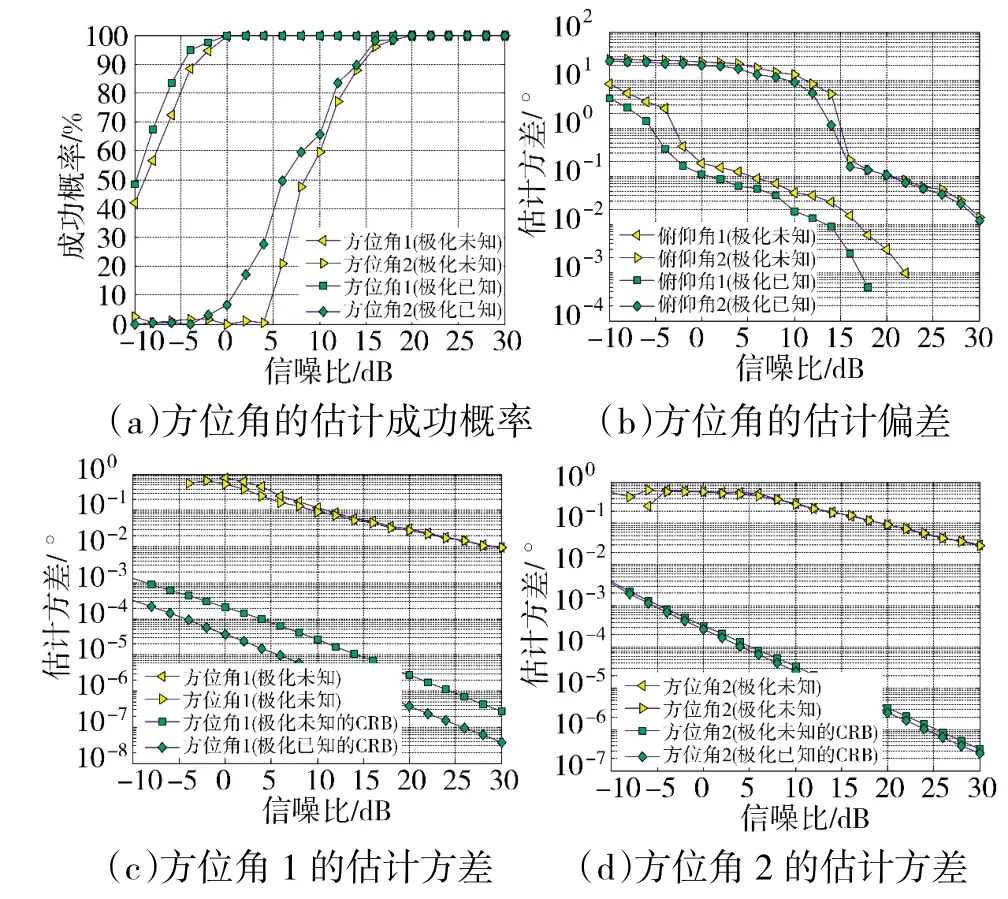
图4 方位角的估计效果曲线
由图3 和图4 可知,在低信噪比条件下,文中所提互耦误差校正算法在信源方位估计方面性能略差于极化参数已知时的互耦校正算法;在高信噪比情况下,两者对信源方位的估计成功概率均为100%。表1 中给出了极化参数和互耦系数的估计均值与方差,当信噪比较低时,本文算法估计性能不如极化已知时的估计算法;当信噪比增大时,本文算法估计性能变好,当信噪比大于16 dB 时,估计性能与极化已知时的估计性能相差无几,从而证明了本文算法能够实现信源方位、互耦系数和极化参数的联合估计。
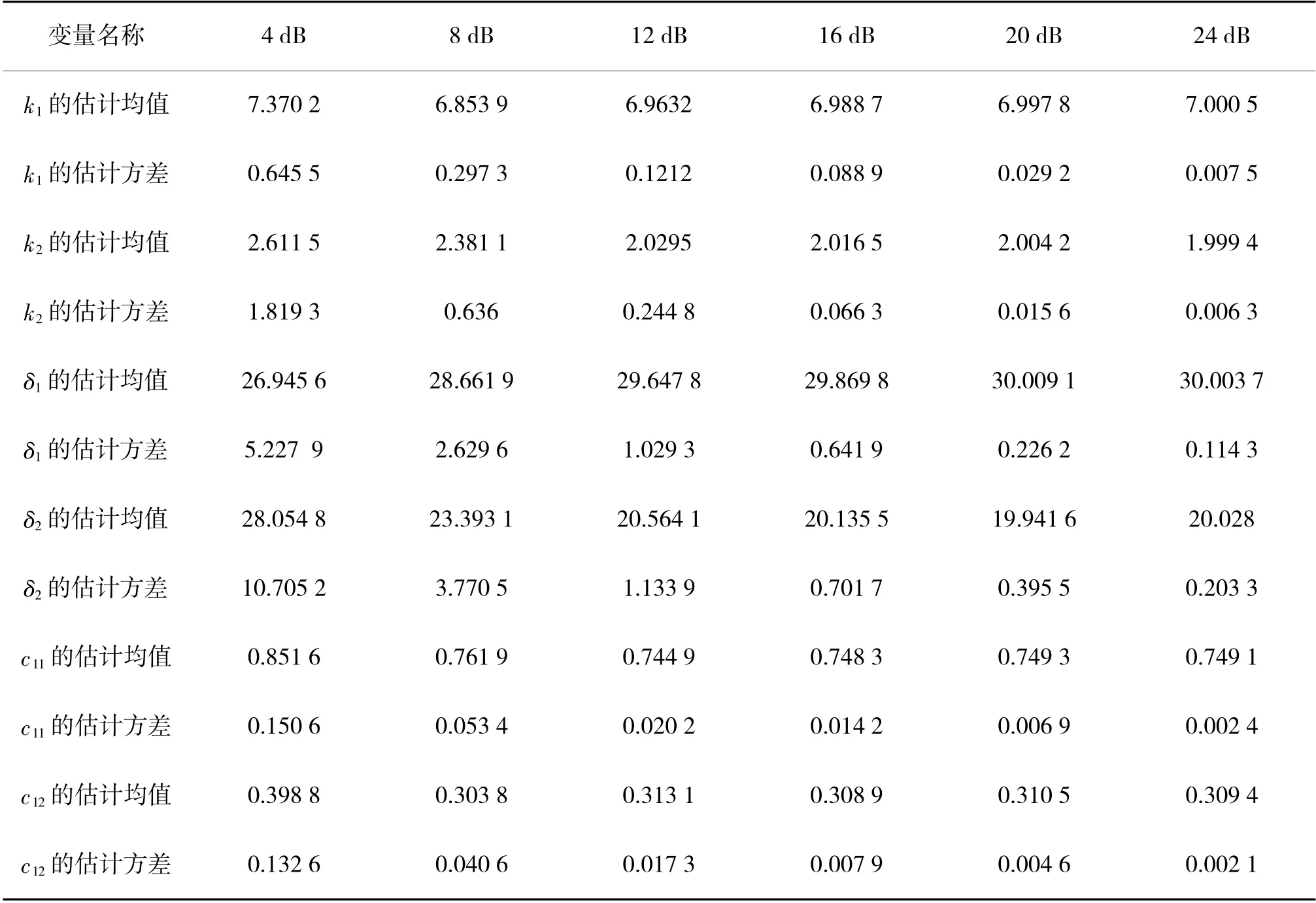
表1 互耦和极化参数的估计(真值为k1=7,δ1=30°,k2=2,δ2=20°,c11=0.749 2,c12=0.309 8)
5 结论
在球面环形共形阵列中,受载体曲率变化的影响,各阵元单元方向图函数不同,致使信源方位、极化和互耦系数同时存在,无法分离,是实现互耦校正算法的难点。本文给出了一种自校正算法,可实现信源方位、极化和互耦系数的联合估计。该算法可实现盲极化条件下的互耦误差校正,且无需参数配对,本文详细推导了算法的理论与一致性。最后MATLAB 仿真,证明本文算法可以很好解决球面环形共形阵列互耦误差校正的难题。
