导弹的直接参数化姿态控制器设计*
2022-10-23薛梦琪刘珊中邱耀龙秦陆明
薛梦琪,刘珊中,邱耀龙,秦陆明
(河南科技大学信息工程学院,河南 洛阳 471023)
0 引言
在现代战场中,随着弹道导弹武器性能不断提高,对反导拦截导弹的拦截精度、响应速度等性能的要求也越来越高。当拦截导弹进入末制导段时,为了搜寻目标,导弹姿态经常需要做快速的角度调整,以实现跟踪并拦截目标。为提高拦截导弹命中目标的成功率,设计高精度、快响应的姿态控制器尤为重要。
当前,很多学者都对拦截导弹的姿态控制问题进行了研究,并提出了很多方法,例如,神经网络控制方法、反馈线性化方法、干扰观测以及鲁棒自适应方法等,将这些方法应用到导弹姿态控制问题中,都能有效提高系统鲁棒性以及跟踪的精度和速度。文献[5]提出了伪线性系统的直接参数化控制方法,针对非线性系统,无需进行解耦线性化处理,直接将其转化为特征值任意配置的线性定常系统进行控制器设计,保留了系统的原有结构,使模型更贴合实际,具有理论指导意义,且闭环特性良好,实用性广泛。而滑模控制的算法简单,响应快,不依赖被控对象精确的数学模型,适用于对导弹复杂非线性系统的跟踪控制设计,具有良好的系统控制性能。
1 三通道耦合姿态数学模型的建立
拦截导弹大多为轴对称体,在飞行过程中具有变质量、变外形、弹性或塑性形变等特点,弹体运动方程十分复杂。在建立拦截弹姿态数学方程时做如下假设:1)将弹体视为常质量刚体;2)略去一些次要的影响因素,例如,地球自转、大气环境、重力等。基于欧拉姿态角建立拦截导弹姿态数学方程,具体描述如下:
根据动量矩定理,建立弹体绕质心运动的动力学方程:

根据姿态角与旋转角速度之间的关系,建立弹体绕质心运动的运动学方程:

为确定导弹空间姿态,建立弹体相对于地面坐标系的姿态运动方程:
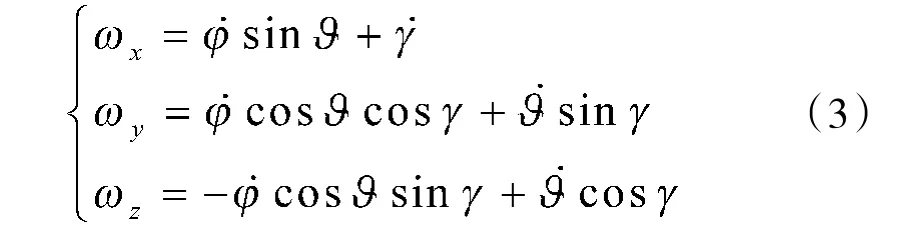
将上述方程式(1)、式(2)联立,并分解为3 个子系统:俯仰、偏航、滚转,可得到二阶方程式(4),再将式(1)代入式(4),联立式(3)消去参数ω、ω、ω及其微分项,通过推倒计算得到仅存在3 个角变量的方程组,即拦截导弹姿态数学模型式(5):


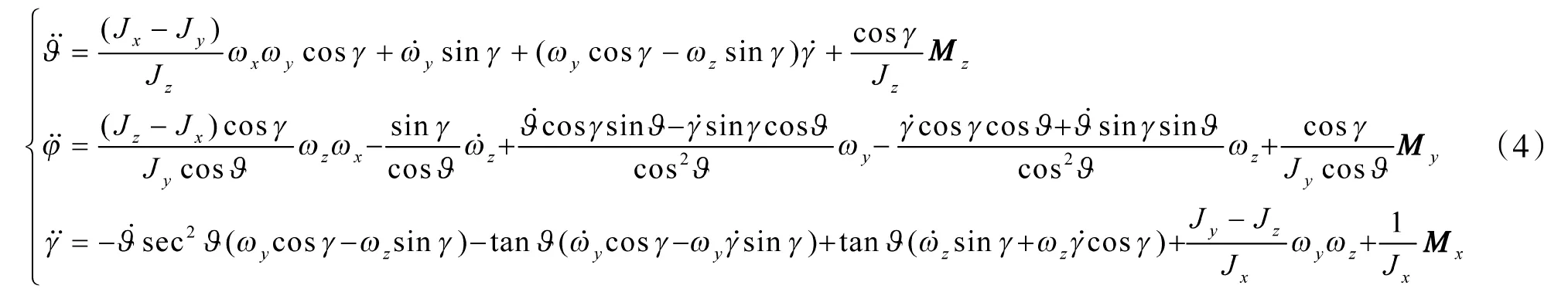
2 直接参数化稳定控制器设计
2.1 直接参数化方法
对于二阶非线性系统模型式(8):
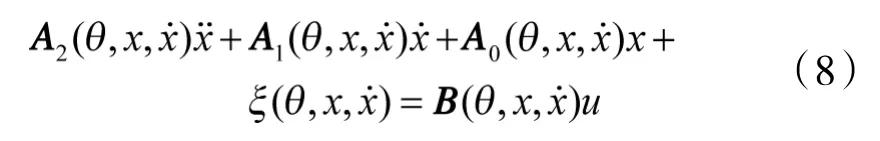
若满足文献[5]的3 个假设条件,可对该系统模型设计控制器,使得到相应的闭环系统式(9)转化为有期望特征值的线性定常系统。

式中,



定义:




2.2 直接参数化稳定控制器设计
Step 1:对于拦截导弹姿态数学模型式(5)满足3 个假设条件:
1)姿态模型中不存在θ(t);

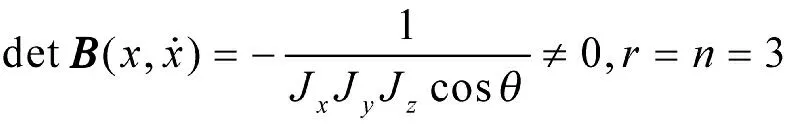




Step 3:选取极点配置矩阵:

选取自由参数矩阵初始值:


根据闭环系统特征值灵敏度优化指标式(11),采用MATLAB 工具箱fmincon 优化函数,固定F 不变,对Z 进行优化。



根据引理可知:


得到反馈控制器:
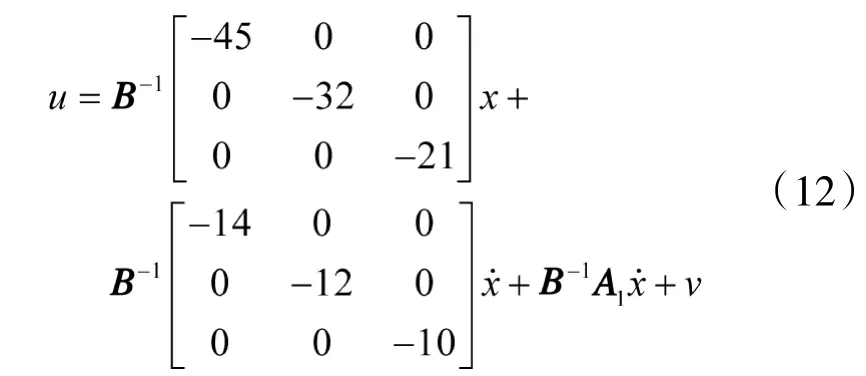


显然,镇定后的矩阵与理论矩阵一致,在该控制器作用下闭环系统稳定。
2.3 仿真分析
智能控制实验室(ICLS)主要用于精确制导武器系统的半实物仿真试验,为导弹飞行试验成功奠定基础,其仿真系统的实物主要是三轴转台和机柜,三轴转台具有三轴速率和三轴位置功能,用于模拟导弹在飞行过程中的姿态变化,机柜用于支持各仿真子系统软件的运行。智能控制实验室平台仿真模型弹体参数如下:发射初始质量:m=225 kg;弹体 直 径:d=0.299 m;转 动 惯 量:J=3.45 kg·m,J=J=60.85 kg·m。


图1 姿态角响应曲线
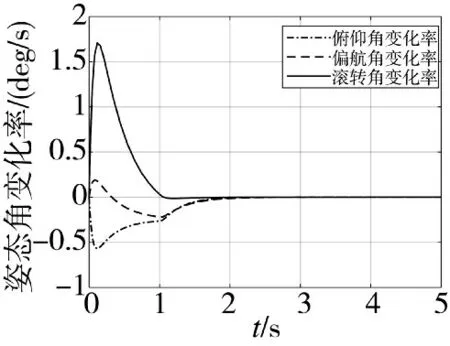
图2 姿态角变化率响应曲线
由图1、图2 可知,基于直接参数化方法设计的控制器可使系统模型在3 s 内迅速镇定,且状态变量都渐近稳定到零,满足设计要求。
3 滑模跟踪控制器设计
3.1 控制器设计

设计滑模切换函数为:


采用指数趋近律:



3.2 稳定性分析


根据Lyapunov 渐近稳定定理可知系统最终将到达并保持在滑动模态上,系统在Lyapunov 意义下渐近稳定。
4 仿真分析
根据上述设计的控制器,搭建SIMULINK 闭环仿真模型,检验在外加干扰情况下所设计控制器的指令跟踪效果,并与PD 跟踪控制做仿真对比,验证了滑模跟踪控制的先进性。拦截导弹的姿态跟踪要求满足最大滚转指令为90°,指令跟踪误差小于2%,调节时间小于0.6 s,超调量小于20%。

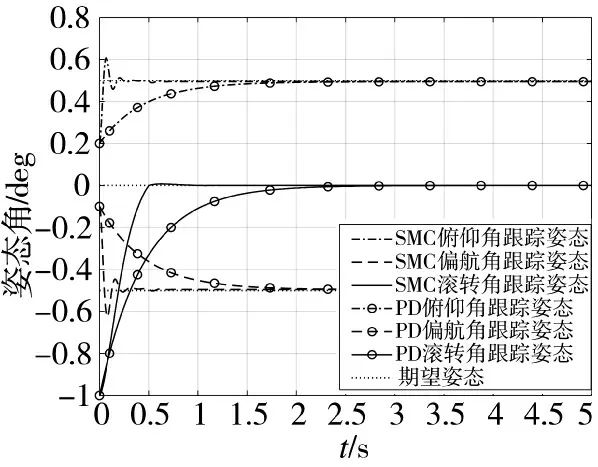
图3 定值信号时姿态角跟踪曲线

图4 定值信号时姿态角跟踪误差曲线

图5 时变信号时姿态角跟踪曲线
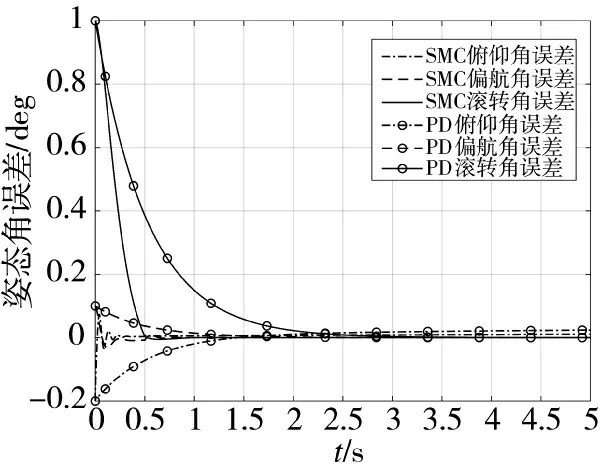
图6 时变信号时姿态角跟踪误差曲线
2)给定指令信号:
由图3~图6 可知,当给定两种指令信号时,PD跟踪控制跟踪速度较慢,存在较大跟踪误差;而滑模跟踪控制可以使俯仰角、偏航角、滚转角在0.6 s内从初始状态渐近跟踪到期望指令信号,且都保持期望姿态角稳定不变,跟踪误差小于2%,超调量小于20%,满足姿态控制要求。
5 结论
直接参数化控制器设计形式简单,能将高度的非线性姿态控制系统转化为有期望特征值的线性定常系统。因此,本文针对拦截导弹末制导段弹体飞行姿态控制问题,以耦合状态下拦截导弹三通道非线性数学模型为对象,无需对其进行解耦线性化处理,采用直接参数化方法设计稳定控制器,仿真结果表明,在存在扰动的情况下,直接参数化稳定控制器可以使系统在3 s 内迅速镇定且具有良好的鲁棒性,验证了控制器的有效性;其次,设计滑模姿态跟踪控制器与直接参数化稳定控制器结合,搭建SIMULINK 仿真模型,并与PD 跟踪控制对比;仿真结果显示,在存在扰动的情况下,给定两种指令输入信号,本文所设计的滑模跟踪姿态控制器可以使模型输出快速有效地跟踪指令输入信号,且跟踪误差小于2%,超调量小于20%,满足拦截导弹姿态控制器的设计要求。
