基于核心素养的教学设计维度思考——以《诱导公式》教学设计为例

陈艳华 康博宇

(1牡丹江市教育教学研究院， 黑龙江 牡丹江 157000 2海拉尔伊敏小学， 内蒙古 呼伦贝尔 021000)

课堂教学是培养人才的主要途径，学生的学习效果与教师教学方法息息相关，从前提倡的素质教育和现在倡导的核心素养培养都是以提高学生提出问题解决问题能力提升为目的，培养学生的创新能力成为创新型人才，这是教育永恒不变的主题，是每个阶段教育的共同目标，教师在课堂教学设计时要把握这个目标，围绕培养学生核心素养进行多角度思考，把教学内容“包装设计”，用灵活多样的教学方法调动学生学习主动性，促进学生探究，循序渐进挖掘知识内涵，理解知识的本质特征，调动学生研究知识的内动力，达到培养学生学习能力、研究能力、创新能力的目标。

教师的教学设计维度体现在学生主体的发展过程。每节课的教学维度根据什么来设计？应该围绕学生主体，学生主体的发展过程和发展目标以及目标的达成是教师教学维度设计思考的难点。笔者基于学生主体在课堂中的表现，结合人教A版教材必修第一册第五章第三节《诱导公式》的教学设计为例，谈谈教学设计维度的思考。

一、从调动学生主体的兴趣、探究动机和态度维度思考

学生对知识产生探究的兴趣是探究行为发生的动机，教师在教学设计时要思考用什么样的方式促使学生产生兴趣，根据学生年龄的特点，好奇的心理，用具有指向性的问题激发学生产生兴趣，这是一切教学行为有效的前提。学生对问题有浓厚的兴趣，就会产生探究的动机，教师给学生探究的时间和空间，学生态度积极，思考用何种方式、何种手段实现探究目的，其中包括独立思考、小组联手合作、各组彼此争论，寻求教师指导等，这些思维的碰撞会出现创新的火花。

《诱导公式》这节课是学习了三角函数的概念之后，根据定义获得相关公式，是定义的灵活应用，是培养学生数学抽象思维，数学逻辑核心素养的介质，教师进行设计时通过情境的创设提出问题：

1.用实物教具——钟表，用学生身边的实物调动学生主体兴趣。

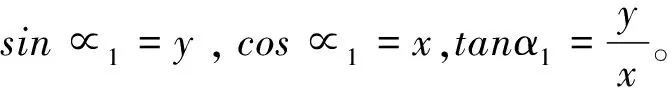
2.学生从兴趣出发产生探究问题动机。教师抛出第二个问题：P1(x,y)关于y轴、原点O、x轴的对称点分别为P2,P3,P4,它们的坐标分别是什么？第三个问题：分别以OP2,OP3,OP4为终边的角∝2，∝3，∝4的正弦值、余弦值、正切值与∝1的正弦值、余弦值和正切值有什么关系？原理是什么？能得到什么结论？学生看到问题后产生强烈探究欲望，教师适时给8分钟的时间(根据学生探究情况可以增加时间)请学生探究问题的真相。

此处对教材呈现的顺序和表现形式进行改编，教材先从关于原点的对称开始，以问题链搭建思维的脚手架，使学生从兴趣出发产生探究的动机，推理知识的发生发展过程，找到数学的概念规律。教育是长期行为，教师根据学生主体特点，使用恰当教学手段，调动学生学习兴趣和探究动机，进一步实施教学过程，培养学生探究知识发生发展过程获得真知的行动力。

二、从学生主体的思考力、判断力、表达力培养与提升的维度思考

学生的思考力是对教师设计的相关问题思考能力，与教师设计问题的难度和梯度有关，若教师设计的问题过于简单，学生不用过多思考即随口答出，这样的问题就是无效问题；若教师设计的问题过难，学生长时间思考也无法解决，课堂教学无法顺利实施，也是无效问题。教师的问题设计要科学合理，符合学生知识结构和思维特点，学生经过思考或者合作探究能够做出合理判断或者形成合理争论点，大部分学生能够合理表达判断结论和争论观点，通过这样一个个有效问题，难度梯度逐渐上升，形成问题链，逐渐呈现知识的发生发展过程并顺利抽象出相关概念，有效培养学生思考力、判断力、表达力的提升，形成良性循环。

前面三个问题学生用了8分钟左右时间探究，或独立思考，或小组谈论，或多方求助等，做出相关判断，教师请学生到前面表达自己的观点。(为了表达充分，给学生12分钟左右时间表达并且总结，如果时间不够可以增加调整，重复表达可以增强学生的记忆)

学生1：我首先回答对称点的坐标，P1(x,y)关于y轴的对称点落在第二象限设为P2(-x,y)，关于原点的对称点落在第三象限设为P3(-x,-y)，关于x轴的对称点落在第四象限设为P4(x,-y)。

回答非常全面精准，得到全体学生认同，并赢得掌声。学生心里得到满足，促使今后积极参与思考，参与表达。

学生2：根据任意角三角函数的定义可以得到sin∝2=y=sin∝1，又因为∝2=π-α1，可得sin(π-α1)=sin∝1，同理可得cos(π-α1)=-cosα1，tan(π-α1)=-tanα1。

此处学生会有质疑，争论由此展开，教师要给学生争论的机会。

学生3：为什么∝2=π-α1？落在第二象限的角一定这样表达吗？

学生2思考补充回答：这只是一种表达形式，也可以表达为∝2=3π-α1，或者再加上2kπ，等等。经过这样的争论，学生们能进一步理解任意角概念和终边相同的角三角函数值相等。

学生4：与前面同理α3可以表达成π+α1再加上2kπ都可以，我们就用π+α1代表，sinα3=-y=-sinα1，即sin(π+α1)=-sinα1同理可得cos(π+α1)=-cosα1，tan(π+α1)=-tanα1。

学生5：与前面同理，我就不赘述了，∝4可以用∝4=2π-α1或者∝4=-α1表达，所以可以得到sin(2π-α1)=-sinα1，cos(2π-α1)=cosα1，tan(2π-α1)=-tanα1，

sin(-α1)=-sinα1，cos(-α1)=cosα1，tan(-α1)=-tanα1

此处学生得到与教材不同的表达，虽然与前面争论角的表达方式异曲同工，但学生思考很全面，对今后公式的应用灵活便利，教师要予以肯定，并提出表扬。

教师：同学们通过合作探究根据任意角三角函数的定义推导出四个象限角三角函数值与锐角三角函数值的关系转化，我们把这组公式叫做诱导公式。诱导公式不仅可以求任意角三角函数值，同时体现了三角函数的对称性，对称性是数学中很重要的性质，在解决三角函数各种问题中依然有重要作用。同学们根据前面思考问题的方法，结合对称性，还有没有一些创新性的思考呢？此处鼓励学生不局限于教师提出的对称，能够主动思考点P1关于直线y=x对称点P5以OP5为终边的角β与角α1有什么关系？角β三角函数值与角α1三角函数值有什么关系？如果学生不经过教师的提示就能够提出这个创新的问题，说明学生思考力得到了升华，这是最难能可贵的！如果学生不能提出这个问题，教师进一步提示学生从多角度对称方向研究思考问题，留给学生课后思考提出问题或者探究解决，有的学生会继续讨论探究，有的学生可借助预习在教材中找到问题及结论，教师不限制学生获得途径，留待下节课解决的任务，给学生留有悬念，吊起“胃口”，学生会欲罢不能，着急的学生可能马上找时间探究真知！教师教学设计重点是以本节课的教学内容为基点，培养学生主体数学思维发展，引导学生思维碰撞产生思维生长点，积极表达、争论，提出创新的问题，培养学生提出问题解决问题的能力。

三、从知识与技能的发展到理解与升华转化的维度思考

学生主体活动完成公式推导总结提升环节后，公式的灵活应用技能要设计相关例题和习题，除了对教材中的例题习题进行选择和改编，还要选具有促进学生思维创新发展的题目。这个过程教师设计一部分题目，学生根据教师给出的题目进行变式，再思考解决，形成利用公式解决问题的技能。

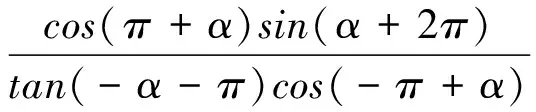
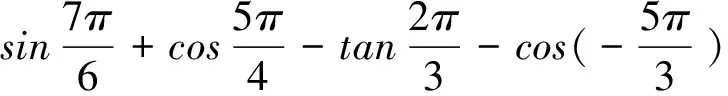
教材例题需要根据学生的情况进行改编使用。本课针对基础好能力比较强的学生，对于特殊角的三角函数值掌握比较熟练，所以把角度表示用弧度制表达，并且把分子分母几个三角函数值化简在综合一起，为后续探究三角函数图像和性质埋下伏笔，训练几个公式的综合应用，达到熟练几个公式的应用技能，也为学生变式问题提供依据。

学生通过独立演算解决完这两个问题后，教师鼓励学生进行变式设计，培养学生提出问题全面性，领会命题意图，多角度培养学生知识转化为技能的方法。学生可能出现多种设计结果，教师给学生机会表达，调动学生主体参与提出问题，设计问题，解决问题，学生在设计变式过程中，思考着公式主体结构的变化，思考着知识涵盖面的广度，思考着解决问题学生心理的变化等等，当老师选择自己题目时，不仅设计的学生有成就感，参与解决问题的所有学生也有积极性。

例1变式：化简下列各式：

(3)sin(π+α)tan(-α)+cos(2π-α)

例2变式：求下列各式的值：

此处都是学生主体活动，由学生命题，学生组织解答，并给予回答学生适当的评价，教师认真聆听，仔细观察学生活动，适当给出指导和评价，学生所编撰题目，已经涵盖各个象限角和三角函数值的几种形式，同时注意范围的扩展，学生主体得到充分肯定，思维拓展深度和广度目标得以实现，无需大量习题，学生变式出题目并组织解决，就能全方位思考知识的应用，学生把知识转化为技能的同时，理解设计问题的意图，通过设计问题能更加深入理解并升华，把知识与技能升华到思维形成数学思想方法和数学核心素养，达到教学设计维度目标。

四、从多方探究到总结升华设计维度思考

课堂教学最后五分钟的总结非常重要，教师应精心设计并做好思维框图，引导学生主体从三个方面总结，一是总结探究知识的发生发展过程，二是总结数学思想方法，三是总结核心素养收获。促使学生回顾思维活动的整个过程，捋顺学生思维，安抚学生思维的兴奋点，形成知识体系并升华为数学思想和核心素养，通过框图的形式迅速纳入学生思维系统，使知识得到归纳升华。最后把前面思考问题：点P1关于直线y=x对称点P5以OP5为终边的角β与角α1有什么关系？角β三角函数值与角α1三角函数值有什么关系？重新提出布置给学生作业，学生课下探究更加充分，为下节课做好探究知识真相铺垫。

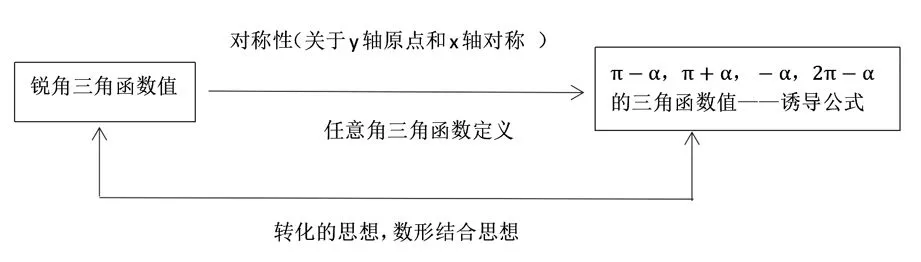
教学相长永无止境，教师根据学生主体情况从四个维度进行教学设计，从创设情境开始引导学生曲径通幽走向柳暗花明，学生从探究活动感悟知识发生发展过程并抽象出理论概念，到提出创新型问题，进一步挖掘概念内涵深入理解灵活应用，开发学生思考力、判断力、理解力、表达力，培养创新能力，在掌握基本知识基本技能的同时，拓展思维广度形成知识体系，达到培养创新型人才的终极目标。