FLNG低温软管内衬波纹管多目标优化设计1)

曹慧鑫 英玺蓬 耿东岭 阎 军

(大连理工大学工程力学系，工业装备结构分析国家重点实验室，辽宁大连 116024)

海上浮式液化天然气（floating liquefied natural gas, FLNG）生产储卸装置系统集天然气的开采、液化、储存和装卸等功能为一体，是一种新型的液化天然气生产系统。与传统的海上天然气开采方式相比，FLNG系统具有节约成本空间、可重复利用、安全性高等诸多优点[1-3]，是我国海洋能源开发领域中“碳达峰”的重大攻关装备。典型的FLNG系统如图1 所示[4]。低温柔性管道是FLNG系统中输送液化天然气的核心装备之一，图2为典型的波纹管型低温柔性管道结构示意图[5]。U型波纹管是位于其中最内层的内衬结构，在进行液化天然气装卸作业过程中直接与液化天然气接触，且需要在海洋波浪载荷及浮体运动下，使其能够承受环境载荷、工作载荷以及随机载荷，保证管道结构的安全性[6]。这使得对U型波纹管进行力学性能分析并进一步开展优化设计具有重要的学术研究和工程应用价值。

图1 浮式液化天然气生产储卸装置[4]Fig.1 FLNG production, storage and unloading device [4]

图2 波纹管型FLNG低温柔性管道[5]Fig.2 The FLNG cryogenic flexible hoses with bellows[5]

目前，国内外学者在波纹管型FLNG低温柔性管道结构性能的分析中已经进行了有益的研究，主要包括基本力学性能、温度介质影响、优化设计及疲劳等方面。周耀兵等[7]研究了316L金属波纹管在海水环境中短时间内出现腐蚀穿孔现象，针对其材料成分、电化学性质和工作环境等方面进行检验和分析，得出了金属波纹管短时间内点蚀穿孔的原因，并提出延长金属波纹管使用寿命的方法。杨亮等[8]基于U 型金属波纹管关键结构参数（波高、波距和壁厚等）完成了管道结构刚度性能的敏感性研究，并总结出拉/弯工况下的最大应力出现位置。熊飞宇[9]同样基于上述结构参数进行了U型波纹管扭转线性屈曲分析，并在此基础上进行了U型波纹管在扭转载荷下非线性屈曲分析。Buitrago等[10]总结了波纹管在环境温度和低温下的结构性能测试的实验方法和结果，进行了波纹管在低温下的拉伸、压缩、弯曲、扭转和内部压力等工况的性能测试。Hao等[11]研究了波形结构参数对金属波纹管失效机理的影响，通过对U型波纹管的反复弯曲过程进行了数值模拟，并提出了一种新型波形结构波纹管，得出设计不等参数的波形结构可以提高金属波纹管的疲劳寿命和抗弯曲断裂性能的结论。

上述研究中大多以波纹管的波高和波距作为结构设计参数研究其对管道力学性能的影响规律。然而由于U型波纹管结构的特性，其波高和波距互相耦合（请见后续第1节详细解释），以波高和波距作为U型波纹管结构设计参数进行灵敏度分析会产生耦合计算的困难。本文针对上述问题，首先对U型波纹管结构进行形状参数分析，得到决定U型波纹管形状互相独立的截面结构参数-波径和环板长度。其次将其作为U型波纹管的结构设计参数，分析了上述设计参数对U型波纹管拉伸刚度、弯曲刚度的灵敏度。基于径向基 (radial basis function, RBF) 神经网络建立了波纹管形状参数与拉、弯性能之间的代理模型，最后基于遗传算法进行U型波纹管结构拉伸刚度最大化、弯曲刚度最小化的多目标优化设计，求解得到了一系列非支配解组成的Pareto最优前沿解集，所得Pareto最优解集可根据具体工程应用的需求确定U型波纹管结构最优的波径和环板长度。

1 U型波纹管结构设计参数与有限元模型

如前文所述，传统研究一般以波高H，波距P作为结构设计参数进行U型波纹管结构分析与优化设计，典型的U型波纹管结构及传统结构设计参数下的截面结构如图3(a)与图3(b)所示。由图中可知，U型波纹管单波结构截面是由波峰和波谷处两个相同的半圆和连接两个半圆的长直板组成。波峰和波谷处两个相同半圆的半径为波径R，连接两个相同半圆的长直板长度为环板长度L。则U型波纹管结构截面的波高和波距几何关系可写为

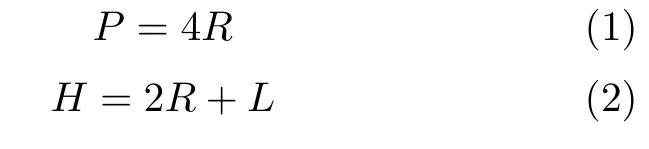
图3 U型波纹管几何模型及波纹结构放大图Fig.3 Geometric model of U-shaped bellows and details of cross-section

从式（1）和式（2）可观察到，当波距P增大时，R随之增大，进而导致波高H也将增大。若以U型波纹管结构的波高、波距作为结构设计参数研究灵敏度影响规律时，两个结构设计参数将互相影响、互相耦合，导致结构的灵敏度分析或优化设计过程产生收敛性困难，甚至发散而得不到优化解。为解决上述问题，本文基于上述对U型波纹管结构参数进行分析，以如图3(c)所示的U型波纹管截面中的波径R和环板长度L作为结构设计参数，二者相互独立，可直接决定U型波纹管的结构形式和尺寸。在进行U型波纹管结构的灵敏度分析和优化设计时，将避免可能的收敛性困难。

本文所研究的U型波纹管采用316L不锈钢材料，弹性模量为200 GPa。U型波纹管的厚度尺寸与整体轴向长度之比远小于1/10，属于典型的薄壳结构。为提高计算效率，采用四节点壳单元建立其数值模型，如图4所示，其单元数量和节点数量分别为17 487和69 948。U型波纹管数值模型的结构参数：波径R= 4.75 mm，环板长度L= 6.5 mm，壁厚t= 0.6 mm，管道内径D= 203.2 mm，波数n= 30，管道模型长度l=570 mm。

图4 U型波纹管数值模型Fig.4 Numerical model of U-shaped bellows

2 U型波纹管结构刚度性能对设计参数的灵敏度分析

2.1 U型波纹管结构拉伸刚度对设计参数的灵敏度分析

为探究U型波纹管的拉伸刚度特征及结构设计参数对拉伸刚度的灵敏度响应，在U型波纹管结构的一端施加固定约束，另一端施加轴向拉伸载荷模拟管道的拉伸行为，计算得到的U型波纹管在拉伸工况下的应力与位移结果如图5所示。从应力云图中可以得出最大Mises应力出现在波峰和波谷位置，其次为环板与半圆连接处，而环板处应力最小。因此U型波纹管承受拉伸载荷时应着重关注波峰和波谷处应力值，即波峰和波谷处最易发生破坏。

图5 拉伸载荷下U型波纹管数值模拟结果Fig.5 Numerical simulation results of U-shaped bellows under tensile load

考虑到FLNG实际工程应用要求，按照工程经验U型波纹管环板长度L和波径R的值一般在一特定范围内，即 ( 0.5≤(2R+L)/(4R)≤1.5)[12]。为研究U型波纹管的结构设计参数波径R和环板长度L对U型波纹管拉伸刚度的灵敏度影响，先控制L及其他所有结构参数不变，分别取R为4.5 mm，4.75 mm，5 mm，5.25 mm，5.5 mm，5.75 mm，6 mm，6.25 mm，6.5 mm，6.75 mm等10个参数变量进行拉伸性能分析。同理，再控制R及其他所有结构参数不变，分别取L为4.5 mm，5 mm，5.5 mm，6 mm，6.5 mm，7 mm，7.5 mm，8 mm等8个参数变量进行分析。通过数值模拟提取端部轴向反力F与轴向位移Δl（拉伸刚度EA=Fl/Δl，l为波纹管长度）[13]，由此可得到波径R和环板长度L对U型波纹管结构拉伸刚度的影响曲线，如图6所示。从图6中可发现，当L不变时，U型波纹管的拉伸刚度随R的增大而减小，这是由于增大R将会导致U型波纹管局部截面的径向长度增加，波纹管中每个单波的伸长量随之增加，进而使得U型波纹管受拉伸载荷的伸缩位移增加。从而使得U型波纹管的拉伸刚度减小，波纹管具有更好的拉伸柔顺性。同理，当R不变时，增大L也导致U型波纹管受拉伸载荷时伸缩位移以及单波伸长量增加，使得U型波纹管的拉伸刚度减小，波纹管也具有更好的拉伸柔顺性。

图6 拉伸刚度EA随结构设计参数变化曲线Fig.6 Variation curve of tensile stiffness EA with the increase of basic structure parameters

2.2 U型波纹管结构参数对弯曲刚度的灵敏度分析

为探究U型波纹管的弯曲刚度特征及结构设计参数对弯曲刚度的灵敏度响应，在U型波纹管结构的一端施加固定约束，另一端施加径向转角位移模拟U型波纹管的弯曲行为，得到的U型波纹管在弯曲载荷下的应力与位移结果如图7所示。从应力云图中可以得出最大Mises应力出现在弯曲转角平面内上下表面的波谷处，其次为该平面上下表面的波峰处，环板处应力很小，且应力分布从上下两侧向中间递减，最终在管道中间位置形成应力较小的中性轴。

本节对U型波纹管的弯曲性能进行设计参数（环板长度L和波径R）的灵敏度分析，通过数值模拟提取端部轴向反力F与径向转角θ（弯曲刚度EI=Fl2/(2θ) ，l为波纹管长度）[13]，得到了其弯曲刚度随波径R以及环板长度L变化的曲线，如图8所示。从图8(a)中可发现，U型波纹管的弯曲刚度随环板长度L的增大而减小。这是由于L的增大会导致波纹管受弯曲载荷时的弯曲柔顺性增加，使得弯曲刚度降低。从图8(b)中可发现，弯曲刚度随着R的增大呈现先减小而后增大的趋势。这是由于增大R会使得波纹管单波结构径向长度和轴向长度同时增加，增加波纹管单波的轴向长度（波纹管总长一定时，相当于波数减少）会导致U型波纹管结构弯曲刚度升高，增加波纹管单波的径向长度（相当于波纹起伏更剧烈）会导致U型波纹管结构刚度降低。随着R的增大，其对轴向长度的影响先小于径向，进而导致弯曲刚度减小。随着R增大到临界值（本例中为6.0 mm处）后，其对轴向长度的影响大于径向，因此导致弯曲刚度又再次增大。

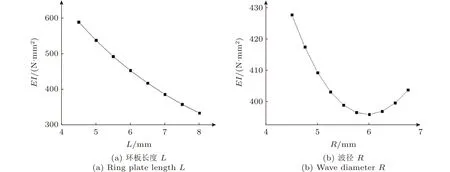
图8 弯曲刚度EI随结构设计参数变化曲线Fig.8 Variation curve of bending stiffness E I with the increase of basic structure parameters

3 基于径向基函数神经网络的代理模型

RBF 神经网络是一种基于径向基函数作为激活函数的神经网络，包含输入层、隐含层、输出层等结构层，其拓扑结构如图9所示[14-15]。其原理是以径向基函数作为隐含层的核函数，将输入信息从低维度映射到高维度，进而能以足够的精度逼近大部分非线性函数，并具有优化函数逼近能力的能力。因此RBF神经网络具有训练数据速度快，以及良好的泛化能力等优点[16]。

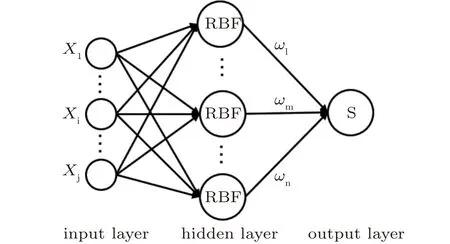
图9 RBF神经网络的拓扑结构图[14-15]Fig.9 Topological structure diagram of RBF neural network[14-15]

3.1 基于RBF神经网络构建代理模型

为保证代理模型准确性并考虑预测效率，选用全析因实验设计方法，结合第2节中的U型波纹管形状参数灵敏度分析，将波径R和环板长度L分别分解为8个和10个水平，共获得8×10组R和L的数据样本，并进行数值计算可得到对应的80组不同U型波纹管结构的拉伸刚度和弯曲刚度。由此，共获得80组数据，每组数据中包含四个参数值，分别为波径R，环板长度L，以及对应该组结构下U型波纹管的拉伸刚度和弯曲刚度。以上述数据集作为构建RBF神经网络代理模型的样本集。本节研究中将样本空间分为两个子集，每个子集包含40组样本，选取第一组子集构建神经网络代理模型，另一组子集用于评估RBF神经网络代理模型的准确性。在RBF神经网络结构中，U型波纹管的波径R和环板长度L作为输入条件，其拉伸刚度和弯曲刚度作为输出信息，通过上述样本训练得出的RBF神经网络代理模型如图10所示。

图10 拉伸刚度与弯曲刚度RBF代理模型三维图Fig.10 Three-dimensional diagram of RBF surrogate model of tensile stiffness and bending stiffness

3.2 代理模型精度验证

通过特定函数选取了80组数据中的40个作为样本点构建RBF神经网络后，利用剩余的40个样本点作为代理模型验证集进行代理模型的精度验证。将40组U型波纹管拉伸刚度及弯曲刚度的数值模拟结果与RBF神经网络代理模型预测结果进行线性拟合，拟合曲线如图11所示，拟合误差分析结果如表1所示。在代理模型误差计算中方差指标R2以及Adjust-R2越接近1代表模型预测越精确[14]，由拟合曲线以及表1中结果可知，U型波纹管的拉伸刚度、弯曲刚度代理模型预测结果与数值模拟结果十分吻合，验证了RBF神经网络代理模型的准确性。

表1 RBF代理模型误差计算Table 1 Calculation Accuracy of RBF Surrogate Model

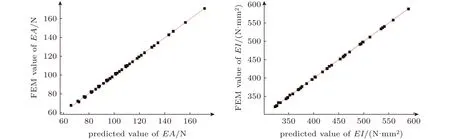
图11 拉伸刚度、弯曲刚度线性回归拟合曲线Fig.11 Linear regression fitting curve of tensile stiffness and bending stiffness

4 多目标优化设计

4.1 U型波纹管优化设计的数学模型

FLNG低温柔性管道主要应用于深远海的天然气开发，环境载荷工况较为恶劣，往往需要柔性管道同时具有较强的轴向抗拉伸性能和较好的横向弯曲柔顺性。因此本节中以内衬U型波纹管拉伸刚度EA最大化和弯曲刚度EI最小化为优化目标，为更直观得到Pareto最优前沿，此处将拉伸刚度EA最大化处理为负拉伸刚度（-EA）最小化。以U型波纹管结构的结构设计参数波径R和环板长度L作为设计变量，并且根据规范要求和实际工艺需要，将设计参数取值限制在固定范围，得到的多目标优化数学模型如式（3）所示。优化设计流程如图12所示。

图12 U型波纹管结构多目标优化设计流程图Fig.12 Flow chart of multi-objective optimization design of U-shaped bellows structure

4.2 优化实例及结果分析

遗传算法是一种受生物进化机制启发的基于全局种群的搜索算法，不易受外界干扰影响，鲁棒性高[17-18]。首先，将种群特征进行编译，并且计算种群初始适应度，接着对初始种群进行选择、交叉、变异操作，生成下一代种群，当遗传代数n达到种群最大代数时，结束寻优过程[17-18]。 遗传算法具有高度并行性、随机性和自适应能力等特点，适用于处理复杂的非线性问题，尤其适用于没有显式表达式的多目标优化问题[19-20]。

通过遗传算法求解上述多目标优化问题所得的Pareto最优前沿解集如图13所示。由图13可知，在Pareto优化解集中，A点表示拉伸刚度最大的单目标优化时U型波纹管的设计，此时抵抗轴向变形的能力最强，但同时弯曲刚度较大，弯曲柔顺性较差；C点表示弯曲刚度最小的单优化目标时U型波纹管的设计，此时弯曲刚度最小，弯曲柔顺性较好，但同时抵抗轴向变形的能力较弱；B点则表示兼顾拉伸刚度与弯曲刚度两个目标时（坐标原点到Pareto前沿距离最短的设计点），U型波纹管结构的多目标优化设计。三个点分别代表的低温柔性管道内衬波纹管层的结构设计方案如表2所示。

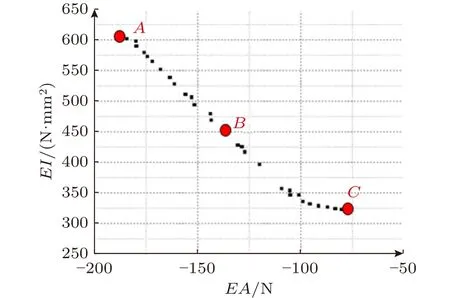
图13 多目标优化的Pareto解集Fig.13 Pareto solution set of multi-objective optimization

从表2中的数据可以看出，虽然A点的拉伸刚度最大（188.2 N），但其对应的弯曲刚度也最大，达到603.8 N·mm2；而虽然C点的弯曲刚度最小，仅为322.7 N·mm2（为A点的一半左右），但其拉伸刚度远远小于A点对应的拉伸刚度（仅为A点拉伸刚度的41%）；而B点较好的同时兼顾了拉伸刚度与弯曲刚度的设计要求，可以更好的满足FLNG低温柔性管道内衬U型波纹管结构的使用要求。

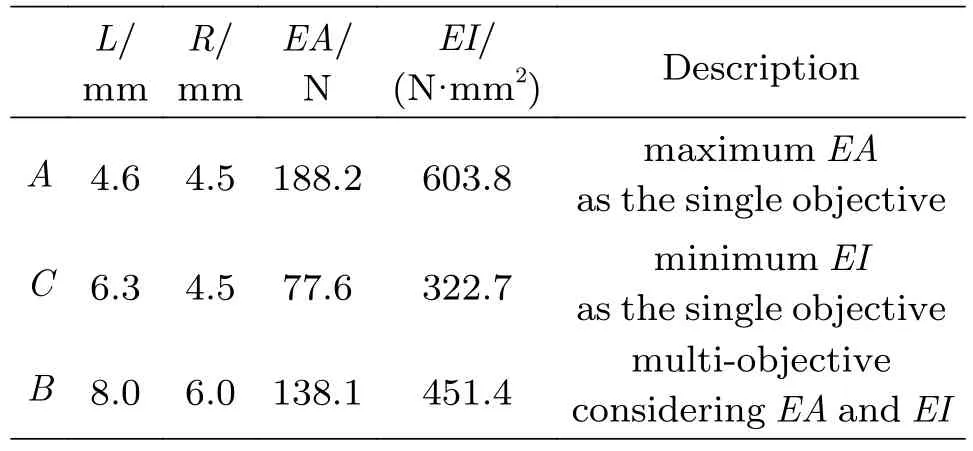
表2 U型波纹管代表性优化设计方案Table 2 Typical optimization designs of U-shaped bellows

5 结论

本文以FLNG低温柔性管道内衬U型波纹管为研究对象，区别于U型波纹管结构设计中传统选择波高、波距参数的设计方法，本文选取波径R和环板长度L作为独立结构设计参数，研究了波纹管的拉伸刚度和弯曲刚度对其波径R和环板长度L的灵敏度规律。解决了在传统的U型波纹管灵敏度分析中，波高会随波距的改变而改变的耦合计算问题。基于RBF神经网络构建了波径R和环板长度L对U型波纹管的拉伸刚度和弯曲刚度的预测代理模型，并验证了其准确性。结合FLNG低温柔性管道的应用背景，采用遗传算法对U型波纹管结构开展了多目标优化设计，获得以拉伸刚度最大和弯曲刚度最小为优化目标时的Pareto最优解集，并得到了满足不同工程需求的三种代表性优化设计方案，为U型波纹管在实际工程应用中提供了有益的设计参考。

目前本文主要讨论了U型波纹管结构的拉伸性能和弯曲性能，因其作为FLNG低温柔性管道的内衬结构层，未来还需对拉伸、弯曲、扭转、内压等多种组合载荷的影响给予充分考虑，并研究超低温环境对U型波纹管结构力学性能的影响规律。