关井状态下油气混输立管的自然频率分析1)

王 振 韩佳琦 李媛媛 王 芳 张德胜 张振楠

*(大连理工大学数学科学学院，辽宁大连 116081)

†(上海海洋大学工程学院，上海 201306)

**(江苏大学流体机械工程技术研究中心，江苏镇江 212013)

††(中国石油大学（华东）储运与建筑工程学院，山东青岛 266580)

近年来，随着深海油气田开发的发展，油气混输海洋立管逐渐受到更多的关注[1]。中国近海蕴藏着丰富的油气资源，但中国近海，尤其是南海和东海区域夏季台风频发，出于安全考虑，海上油气平台和立管系统在遭遇台风等恶劣海况时，选择油气田关井操作是应对策略之一。油气混输立管在台风等恶劣海况下的动力响应关系到平台安全性。油气混输立管的动力响应和安全预报的准确分析对平台的决策十分重要。当深海立管自身的自然频率与由立管所受外力作用的频率相近时，立管的振幅会明显增大，发生复杂的耦合共振现象，导致立管的疲劳损伤甚至失效[2]，从而造成巨大的经济损失和严重的环境污染。

海洋立管振动特性的研究对于了解其动力学行为安全性非常重要，确定立管的自然频率和振型对分析其动力学行为非常关键。Païdoussis等[3]利用物理实验模型和数学模型研究了考虑内部流体流速影响输油柔性管道的动力特性和稳定性问题，进一步确定了内部流体对立管振动特性的影响。由于油气分离以及考虑重力作用，控制方程变成变系数的微分方程，很难解析求解。国内外很多学者对这方面的内容展开了研究，比如Dareing等[4]采用幂级数方法、Kim[5]采用WKB(Wentzel-Kramers-Brillouin)方法、Soltanahmadi[6]基于傅里叶分析方法、Zhang等[7]利用有限元法、Cheng等[8]采用动态刚度法与WKB理论相结合等等一些数值方法来计算立管的振动自然频率和振型。Chen等[9]采用微分变换方法给出8种边界条件下的自然频率和振型，Huang等[10]采用伽辽金法研究了不同边界条件下输流管道流固耦合的自然频率，Xu等[11]利用同伦摄动法系统地导出了具有固支边界条件的流体输送管道的自然频率，Ni等[12]推广了一种新的半解析法-微分变换法，用于分析具有不同边界条件的输流管道的自由振动问题，Chen等[13]用变分迭代法计算了不同边界条件下海洋立管的自然频率和振型，Li等[14]发展了一种新的变分迭代法计算了不同边界条件下的输流管道的自然频率。与单相流情况不同，由于气液相边界处的复杂运动或者相互作用，以及材料性质，如密度、表面张力、黏度等的差异，两相流诱发振动的机制可能会有很大不同。Liang等[15]利用微分求积法分析了不同边界条件下流体输送管道的动态特性。Miwa等[16]在广泛而全面的文献综述基础上，对管道系统两相流诱发振动研究的最新进展进行了全面的回顾和介绍。而后，An等[17]采用广义积分变换技术对输送气液两相流管道的动力学行为进行了分析和数值研究，为管道的自然频率和横向位移提供了高精度的数值解。马晓旭等[18]利用有限元软件ADINA对水平管内气液两相流诱导的振动进行了数值模拟研究，发现含气率的变化对管道振动的固有频率和振型具有明显的影响。Enrique等[19]从理论上研究了两端固定且竖直的输送气液两相流管道的动力学行为，特别是通过伽辽金法研究了流动参数对自然频率的影响。田晓洁等[20]运用ANSYS软件对气液两相流立管振动进行了模态分析，研究了流体边界条件对立管自然频率和振型的影响。

油气混输立管在关井状态下，管道内留存的油气由于重力作用将自然沉降，密度较大的液态介质将沉降到管道的底部，而密度较小的气相更容易聚集在管道的上部，从而导致管道内流体的密度分布和张力分布不均匀，这和管道内流体相对均匀混合的工作状态差异较大，导致管道的振动频率和振动特征发生改变，进而改变动力学行为。台风影响期间，海况环境更加恶劣，对油气混输立管的载荷也更危险，对系统的安全性考验更强，上述振动特性的改变对立管安全影响很大，有必要针对关井状态下的油气混输管道的振动特征单独分析。

本文针对关井状态下的油气混输立管横向振动，首先建立关井状态下油气混输立管横向振动的索模型，给出了能够描绘张力沿索变化的变系数微分方程。然后采用变量分离法，结合边界条件和连接点处位移和斜率变化连续性条件，给出变系数微分方程解的Bessel函数表达式和关井状态下油气混输立管振动的自然频率和模态函数。最后分析关井状态下油气混输立管内体积分数，流体密度和张力变化对立管振动自然频率和模态的影响。对关井状态油气混输立管的安全性评估具有参考意义。

1 数学模型

1.1 控制方程

油气混输立管在分层状态下和混合均匀状态下的结构简图如图1所示，记柔性立管整长为L2，立管顶端平台的顶张力为T，以平台位置为坐标原点，x轴方向为立管垂直向上的方向，y方向为水平方向，也是立管振动位移y(x,t) 的方向。假设立管内部的油气在关井状态下分为两段，连接平台的长度为L1的上段立管内为气态物质，连接水下生产系统的长度为L2-L1的下段管内为液态物质。本文中用到的立管振动物理量及其对应的符号表示见表1。

表1 立管参数符号Table 1 The parameters and symbols of a riser

由于本文考虑长细比较大的柔性管道，所以忽略立管弯曲刚度的作用，采用索模型建立立管的振动控制方程。上段含气段立管单位长度所受的浮力单位长度立管质量单位质量垂向所受合力基于立管微元的受力分析，按照标准的小振幅弦振动方程推导方法，得到立管在x∈[-L1,0] 上的控制方程y1(x,t) 满足

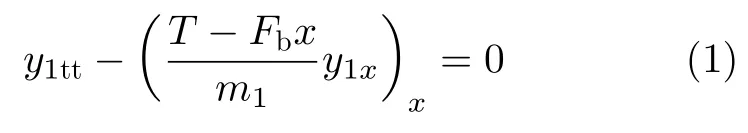
下段含液段立管单位长度所受的重力Fg=单位长度立管质量m2=π

1.2 边界条件

在实际海洋环境中，柔性立管的边界条件经常被理想化成特殊情况。本文假定连接立管的上端海上平台为固定平台，连接立管下端的生产系统也固定不动，在这种理想状态下的边界条件为

同时假设两段立管连接处位移相等，且位移沿立管方向切线斜率相等，则有连续性条件

2 模型解析求解

本节给出由式(1)～式(4)组成系统的求解。

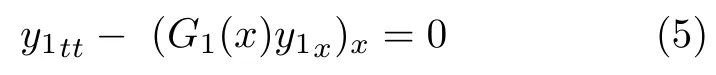
利用变量分离法，令

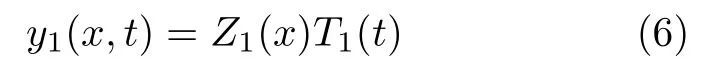
将式（6）代入式（5）得到时间部分满足的方程为

空间部分满足的方程为

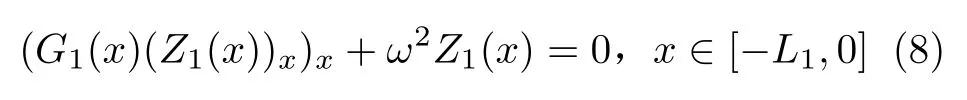
由于方程（8）是变系数方程，故引入变量η，令则空间部分方程可以转化为

这个横向振动方程的空间部分化为零阶Bessel方程，对于方程（10）的解可以用Bessel函数表示

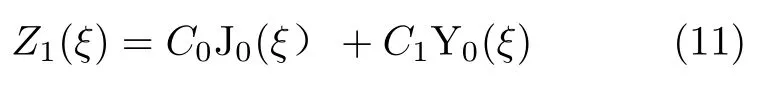
并通过变量变换，方程（8）的解可以表示为

其中C0，C1为任意常数。

与解上段含气段立管振动方程类似，同样利用变量分离法，令

上段含气段立管与下段含液段立管的时间部分是相同的，即T1(t)=T2(t) ，则Z2(x) 满足

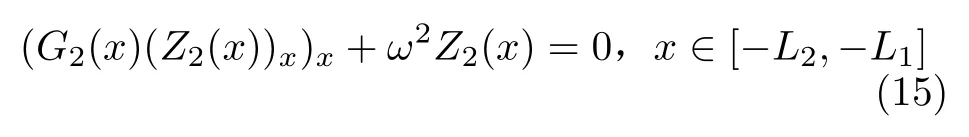
得到下段含液段立管振动方程的模态函数

其中C2和C3为任意常数。

边界条件（3）和连续性条件（4）由变量分离形式（6）和式（14）转化为

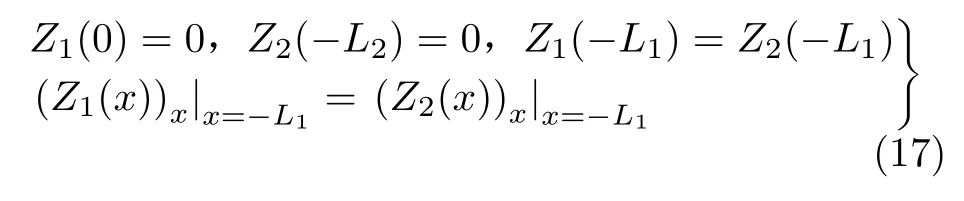
将方程通解形式（12）和式（16）代入到式（17）中得到

欲使方程（18）存在非零解，需满足系数行 列式为0，即

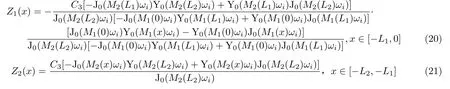
其中C3为任意常数。

为便于模态分析，本文采用如下的模态归一化方法[21]

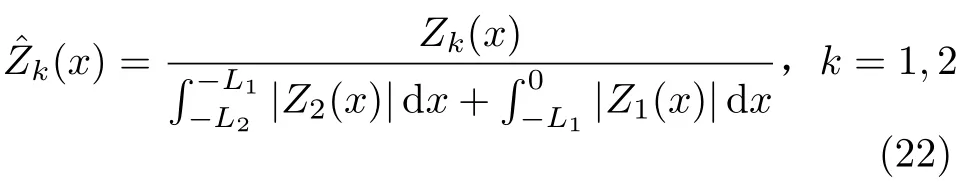
3 自然频率的影响因素分析

3.1 数值算例

本节通过具体算例分析油气混输立管在关井状态下的自然频率和模态函数[22]。柔性立管外径D=355.6mm ， 内 径d=335.6mm ， 密 度ρ1=7850kg/m3，立管上段充满密度为ρ2=1kg/m3的气体，下段充满密度为 9 00kg/m3的原油，海上平台提供的顶张力T=3700N ，重力常数g=9.8N/kg，海上平台到水下生产系统总长度L2=1500m。经计算可知上段含气段立管单位长度质量m1=85.32kg ，单位长度立管所受浮力Fb=137.1477N，下段含油段立管单位长度质量m2=164.84kg ，单位长度立管所受重力Fg=642.1483N。

为了对比分析关井状态下、工作状态下以及均匀张力时立管的振动特征和动力学行为，本文将这三种状态定义为三种工况。

工况1：关井状态，即油气在重力作用下分离直至静置分层。此时气态物质分布在立管的上半段，液态物质分布在立管的下半段。在本文算例中假定上段气态物质为天然气，下段液态物质为原油。在关井状态下假设上段含气段立管长度L1=750m ，则下段含油段立管长度也为 7 50m ，其余物理量按照算例中的参数选取。

工况2：工作状态，即柔性立管内天然气与原油混合均匀。为了便于与关井状态对比分析，与L1=750m 对应，假设工作状态时为立管中原油、天然气体积分数各一半混合均匀。通过本文算例中具体参数，算得工作状态时柔性立管的单位长度质量m=125.08kg ，单位长度立管所受重力Fg=252.5020N 。

工况3：张力分布均匀状态，为了便于与关井状态、工作状态对比分析，本文是在油气分离静置分层后即L1=750m 时，通过上段含气段立管张力积分与下段含油段立管张力积分求和取得总张力，再平均分布到立管总长取得平均张力，即平均张力公式为

通过本文算例中具体参数，算得的平均张力G=1376.727261N。张力分布均匀状态下柔性立管方程为：ytt-(Gyx)x=0 ，边界条件为：y(0,t)=0,y(-L2,t)=0。

表2给出了工况1到工况3的前6阶自然频率。通过对比三种状态下自然频率发现：关井状态下立管的最低阶自然频率大于工作状态下油气混合均匀时立管的最低阶自然频率，最低阶自然频率相差为6.637%，关井状态其余各阶自然频率均大于工作状态时立管的自然频率；第2阶到第6阶的自然频率相差小于10%。与张力均匀分布相比，关井状态下立管的自然频率总体变大；随着自然频率的阶数升高，工况3与工况1的自然频率之差逐渐减小，从第1阶自然频率相差90.65%到第6阶自然频率相差38.196%，说明两种工况相差较大。关井状态下立管的振动分析更加符合台风期的实际情况，因此有必要对台风期的关井状态进行单独考虑。

表2 三种工况下的前6阶自然频率Table 2 First six natural frequencies under three working conditions

L1=750m前6阶自然频率下归一化模态函数如图2，油气混合均匀时前6 阶自然频率下归一化模态函数如图3，从图2和图3中发现，油气混合均匀时与关井状态下静置分层后立管在各阶模态函数变化规律一致：上段含气段立管振动幅值明显高于下段含油段立管振动幅值；随着模态的增加，最大幅值所对应的腹点越靠近平台，幅值为零所对应的节点也越靠近平台。

图2 L 1=750m 时前6阶自然频率下归一化模态函数Fig.2 Normalized mode functions at the first six natural frequencies when L1=750m

图3 油气混合均匀时前6 阶自然频率下归一化模态函数Fig.3 Normalized mode functions at the first six natural frequencies when the oil and gas mix evenly

图4给出了三种工况即关井状态、工作状态、张力均匀状态下在各阶自然频率下的归一化模态函数，从图中可以看出：与张力分布均匀时相比，关井状态时由于张力不均匀，模态函数形状发生了改变，含气段立管和含油段立管振动幅度不相同，模态函数最大幅值的腹点、幅值为零的节点都更靠近平台；与关井状态相比，油气井工作状态时最大幅值的腹点和幅值为零的节点会比关井状态更靠近平台。

图4 柔性立管的三种工况下在前6阶自然频率下的振型Fig.4 Vibration shapes of flexible risers at the first six natural frequencies under three working conditions

3.2 油气体积分数、液体密度、顶张力对立管模态的影响

在关井状态下，立管内的气态物质与液态物质会出现分层现象，密度较小的气态物质会上升，而密度较大的液态物质则会下沉，当管内的油气体积分数不同，或者管内输送不同密度的液态物质时，这些变化会对立管的自然频率和模态函数产生影响。考虑到立管处于深海环境中，其自然频率和模态函数也会受到平台顶张力的影响。

本文用上段立管长度L1取值的大小来描述在关井状态下上层气体所占体积分数的多少，从而来分析对自然频率及模态函数的影响。通过改变L1的值，来分析对应的各阶自然频率变化规律，如图5，给出了前6阶自然频率随L1的变化图像，从图5中可以看出当L1逐渐增大时，各阶自然频率均逐渐减小，同时发现L1的变化对高阶自然频率影响要大于对低阶自然频率的影响。

图5 L1 对自然频率的影响Fig.5 Effect of L 1 on natural frequencies

本文考虑上段含气段立管长度为100 m，250 m，500 m，750 m，1000 m，1250 m这6个立管状态，并分别计算了每个立管状态的前6阶模态函数，对模态函数归一化处理后，比较了每个模态下随上段含气段立管长度增加的变化，图6给出了在前6阶模态下随L1变化的归一化模态函数，通过对比分析可知如下。

（1）在每个模态下，以图6(b)为例，当L1=100m时，上段含气段立管的振动幅度在0.0015～0.002之间，下段含油段立管的振动幅度在 0.0005～0.001 之间，明显小于含气段立管的振动幅度；当L1=250m 时，上段含气段立管的振动幅度在 0.002～0.0025 之间，下段含油段立管的振动幅度在 0.0005～0.001 之间；当L1=1250m时，上段含气段立管的振动幅度在0.001～0.0015之间，下段含油段立管的振动幅度在0.0005～0.001之间。由此可见，随着L1的变化，上段含气段立管的振动幅度均大于下段含油段立管的振动幅度，分析图6其他各阶自然频率的模态函数图像，结论一致。

（2）取含气段立管长度为 2 50m ，观察图6(a)～图6(f)中L1=250m 对应的各阶归一化模态函数，在第1阶自然频率下，最大腹点的位置大约在 2 30～250m 之间；在第2阶自然频率下，最大腹点的位置大约在 1 00～120m 之间；在第3阶自然频率下，最大腹点的位置大约在70～90m之间；在第4阶自然频率下，最大腹点的位置大约在 5 0～70m 之间；在第5阶自然频率下，最大腹点的位置大约在 4 0～50m 之间；在第6阶自然频率下，最大腹点的位置大约在30～40m之间。由此可见：当含气段立管长度固定时，随着自然频率阶数的增加，立管各阶模态函数的最大腹点越来越靠近平台；振动幅度最大的立管位置也会随着自然频率阶数的增加而靠近平台。

（3）在各阶自然频率下，以图6(a)为例，L1=100m 时，最大腹点大约在 1 0 0～200m 之间，L1=250m 时，最大腹点大约在 2 3 0～2 5 0m 之间；L1=500m时，最大腹点大约在 2 50～270m 之间；L1=750m 时，最大腹点大约在270～290m之间；L1=1000m 时，最大腹点大约在290～310m 之间；L1=1250m 时，最大腹点大约在310～330m 之间。由此可见：随着L1的逐渐增大，即管内气体逐渐增加时，最大腹点逐渐向左侧即深水方向移动，分析图6其他各阶自然频率的模态函数图像，结论一致。

柔性立管内液体密度的变化也会对立管的自然频率产生影响。关井状态下，立管静置分层，上段为气态物质，下段为液态物质。在考虑液体密度变化对立管自然频率影响的过程中，本文假定立管上段气态物质的密度保持不变，其余各物理量参数均不变，只改变下段液态物质的密度，如图7，随着管内液体密度减小，立管各阶自然频率逐渐减小，但总体变化较为平稳。

平台处的顶张力的改变也会影响立管的自然频率。考虑关井状态下，上段含气段立管和下段含液段立管的长度和密度均保持不变，即上段立管长度为 7 50m ，管内仍为天然气，下端立管长度为 7 50m ，管内为原油，其余各物理量参数不变，仅改变平台处的顶张力大小，如图8所示。随着海上平台顶张力的增加，立管各阶自然频率逐渐增加，但总体变化也较为平缓。同时，结合图7和图8可见：顶张力和密度的变化对高阶自然频率影响比对低阶自然频率影响较明显。

图7 密度对自然频率影响Fig.7 Effect of density on natural frequencies

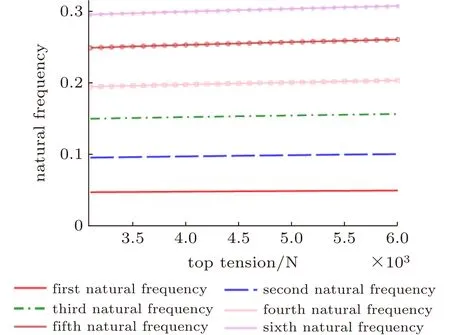
图8 顶张力对自然频率影响Fig.8 Effect of top tension on natural frequencies

4 结论

本文分析了海上油气混输系统在关井状态下，油气分层导致立管内张力和液体密度分布不均匀问题，建立了分段立管横向振动的数学模型，求解出自然频率和模态函数表达式，分析了油气占比、液体密度、顶张力对立管振动特征的影响，并与油气混合均匀、张力均匀时做对比分析，得到结论如下。

（1）基于分离变量方法，给出了关井状态下立管横向振动的自然频率和模态函数的表达式，和工作状态以及张力均匀假设下的立管振动自然频率对比发现，三种工况的自然频率相差较大，有必要单独分析关井状态工况。 通过关井状态与工作状态立管的自然频率、模态函数作对比分析发现，相比油气井工作状态，关井状态下除最低阶自然频率变大外，其余各阶自然频率均小于工作状态时自然频率。

（2）通过关井状态与张力均匀分布时立管的自然频率、模态函数作对比分析发现：相比张力均匀，关井状态下静置分层后立管的自然频率大，且低阶频率对张力改变更加敏感；关井状态下最大幅值的腹点和幅值为零的节点向平台方向移动。

（3）随着柔性立管含气段长度逐渐增大，立管的自然频率逐渐减小；下段管中液态物质密度越大，立管的自然频率越大；平台顶张力越大，立管自然频率越大。对于各阶模态函数，上段含气段管的振动幅度大于下段油管的振动幅度，且随着上段含气段管长度逐渐增加，最大腹点会向深水方向移动。