表面微织构对气体动压轴承承载性能的影响
2022-10-21丁浩高强冯伟刘保国李行雨
丁浩,高强,冯伟,刘保国,李行雨
(1.河南工业大学 机电工程学院,郑州 450001; 2.河南省超硬磨料磨削装备重点实验室,郑州 450001)
气体动压轴承使用气体作为润滑剂,具有结构简单,转速高,摩擦小,无污染等优点,在航空航天、纺织机械、高速离心分离机、低温运转制冷机等方面有着极为广阔的应用前景[1-5]。随表面光刻技术的发展,微织构表面对于机械产品性能提升的研究开始受到关注。气体动压轴承承载能力弱, 可以考虑在气体动压轴承表面加工微织构,微织构会影响气膜流动,进而改变气体动压轴承的承载性能,合适的微织构形状和深度有利于提高气体动压轴承的承载性能。
气体动压轴承的研究多采用经典的雷诺方程或Navier-Stokes方程计算气体润滑模型,当气膜厚度小于气体分子的平均自由程时,上述方法不再适用[6],需考虑气体稀薄效应的修正模型;而大部分气体动力学方程均基于宏观连续性假设进行计算,对于微小间隙的气体流动仍缺乏合适的解算方程:故微织构气体动压轴承的承载性能研究缺乏有效的理论支持,尤其是高流速、小间隙的情况。在非均衡的统计结构中,基于微观分子动力学的Lattice Boltzmann Method(LBM)可以从中观或者介观比例建立流体行为模型,Lattice Boltzmann方程已经被广泛应用于多孔介质流,页岩气微观流动,微间隙旋转流动,方腔流动,库埃特流动等领域的计算,在微观流动计算领域具有一定的可行性基础[7-27]。
本文基于LBM建立了气体动压轴承计算流体动力学模型,并分析了微织构形状和深度对气体动压轴承承载性能的影响。
1 基于LBM的气体动压轴承计算流体动力学模型
1.1 LBM模型
LBM源于格子气自动机方法,一个完整的模型通常包括离散速度模型、平衡态分布函数、分布函数演化方程,模型构建的关键点在于选取合适的平衡态分布函数,而平衡态分布函数的具体形式又和离散模型的构建有联系,离散速度的对称性决定了Lattice Boltzmann模型能否还原到所要求解的宏观方程。
LBM的D2Q9离散化速度模型如图1所示,D为模型维度,Q为离散速度数量,D2Q9模型表示格子在2维平面中具有9个离散速度。速度配置为[4]
(1)
c=δx/δt,
式中:eα为离散速度;α为方向角度;δx为网格步长;δt为时间步长。

图1 D2Q9模型
平衡态分布函数为
(2)
为还原宏观方程,将平衡态分布函数适应如下方程
(3)
(4)
(5)
化简后模型的宏观密度、速度、宏观压力状态方程定义为
ρ=∑αfα,
(6)
(7)
(8)
式中:ρ为密度;ωa为权系数;u为移动速度;Cs为格子声速;P为压力。
一般的一维流动方向(ci,cj)上的格点和壁面情况如图2所示,该图展现了一维流动的格点碰撞原理,图中:xf1,xf2,xf0为流体区域的格点,xw,xδ为固体区域的格点,ci,cj为碰撞方向,q为格点数,Δx为单个格点长度。此时
(9)

图2 曲面边界格点分布示意图
曲面边界的反弹格式有格点反弹式(对于物理边界用最近的格点近似去代替,并将标准的反弹格式直接用于这些边界格点进行计算)和格线反弹式(将该格式与边界相交格子线的中点作为边界格子点,并在这些点位上应用half-way反弹格式)2种处理方法,格线反弹式中无论q取多少,格线的反弹格式都将以(xf0+xδ)/2作为边界条件格点,反弹格式如图3所示。

图3 曲面边界的反弹格式
1.2 气体动压轴承计算流体动力学
气体动压轴承的承载力通过动压效应产生,在稳定状态下气体动压轴承的模型类似于箔片气体动压轴承,此时箔片和轴径中间充斥着稀薄的气膜,箔片被撑开的形状是固定的。由此,建立气体动压轴承简化计算流体动力学(Computational Fluid Dynamics,CFD)模型如图4所示,图中:O1为旋转轴中心,O2为轴承中心,R1为旋转轴半径,R2为瓦块半径,e为偏心距,θ为偏心角,ω为转速,Cr为气膜厚度。轴和瓦块所受的力大小相等,方向相反。通过瓦块壁面沿y轴正方向的总压力来衡量轴承承载能力。

图4 气体动压轴承简化模型示意图
气体动压轴承的网格分布如图5所示,边界格点既可以在固体区域,也可以在流体区域。流体区域的格点被称为流体格点,固体壁面等区域的格点被称为固壁格点。
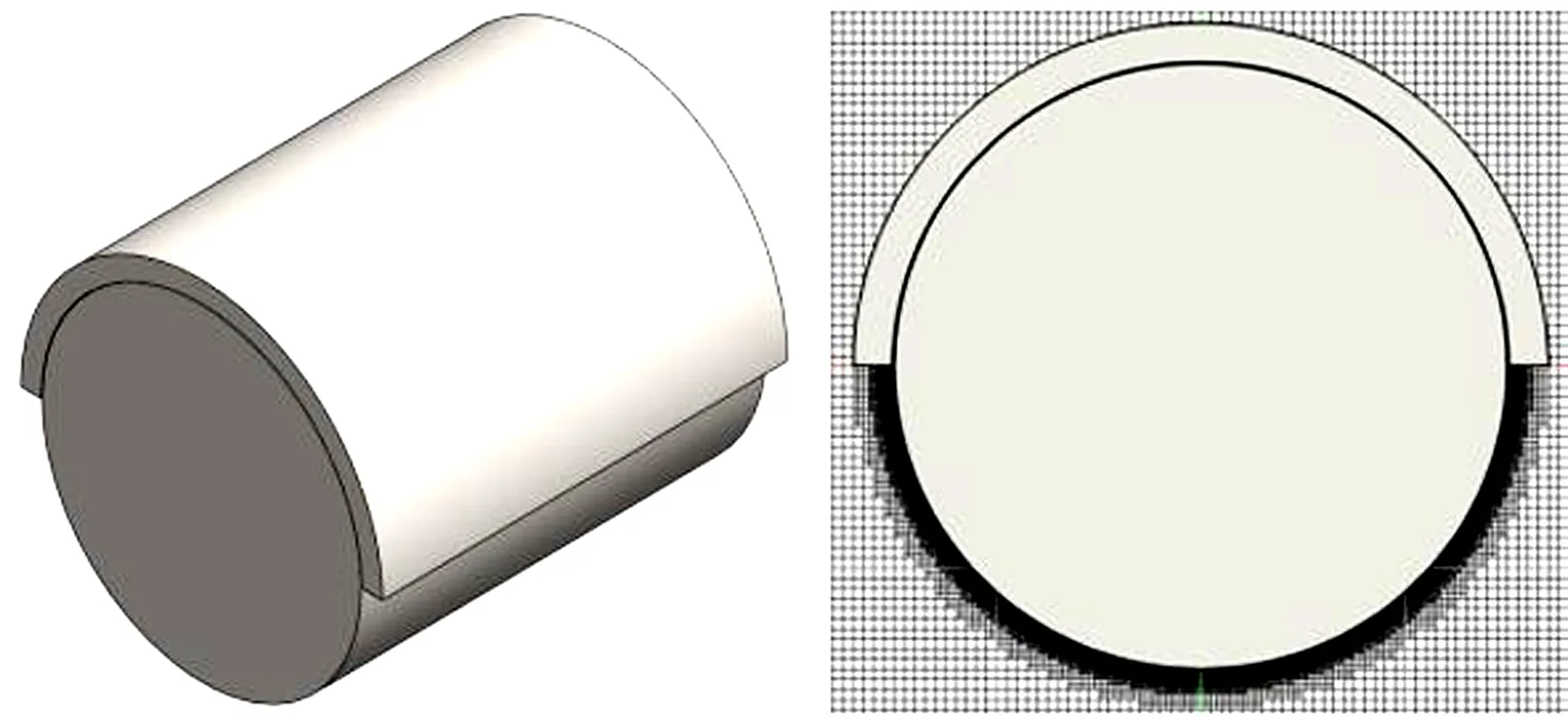
(a) 轴承模型
格点反弹式和格线反弹式均采用折线近似物理边界,当这些边界上的格子足够小时,相当于无穷接近曲边边界。实际计算时格子不能过小,否则会导致边界网格计算量过大而无法计算。
物理边界格子的加密过程如图6所示,红线为旋转轴边界,黑线为瓦块边界,对于格子覆盖不到的曲边边界,邻近的格子会自动插值求解。
2 模型验证
以光滑表面气体动压轴承为例验证,主要结构参数为:轴承直径31 mm,轴承长度38.1 mm,平均气膜厚度70 μm,偏心率0.202。偏心率固定时承载力、气膜流速、气膜压力随转速的变化分别如图7—图9所示。

图7 光滑表面气体动压轴承承载力随转速的变化曲线

(a) 12 000 r/min (b) 16 000 r/min (c) 20 000 r/min (d) 24 000 r/min (e) 28 000 r/min
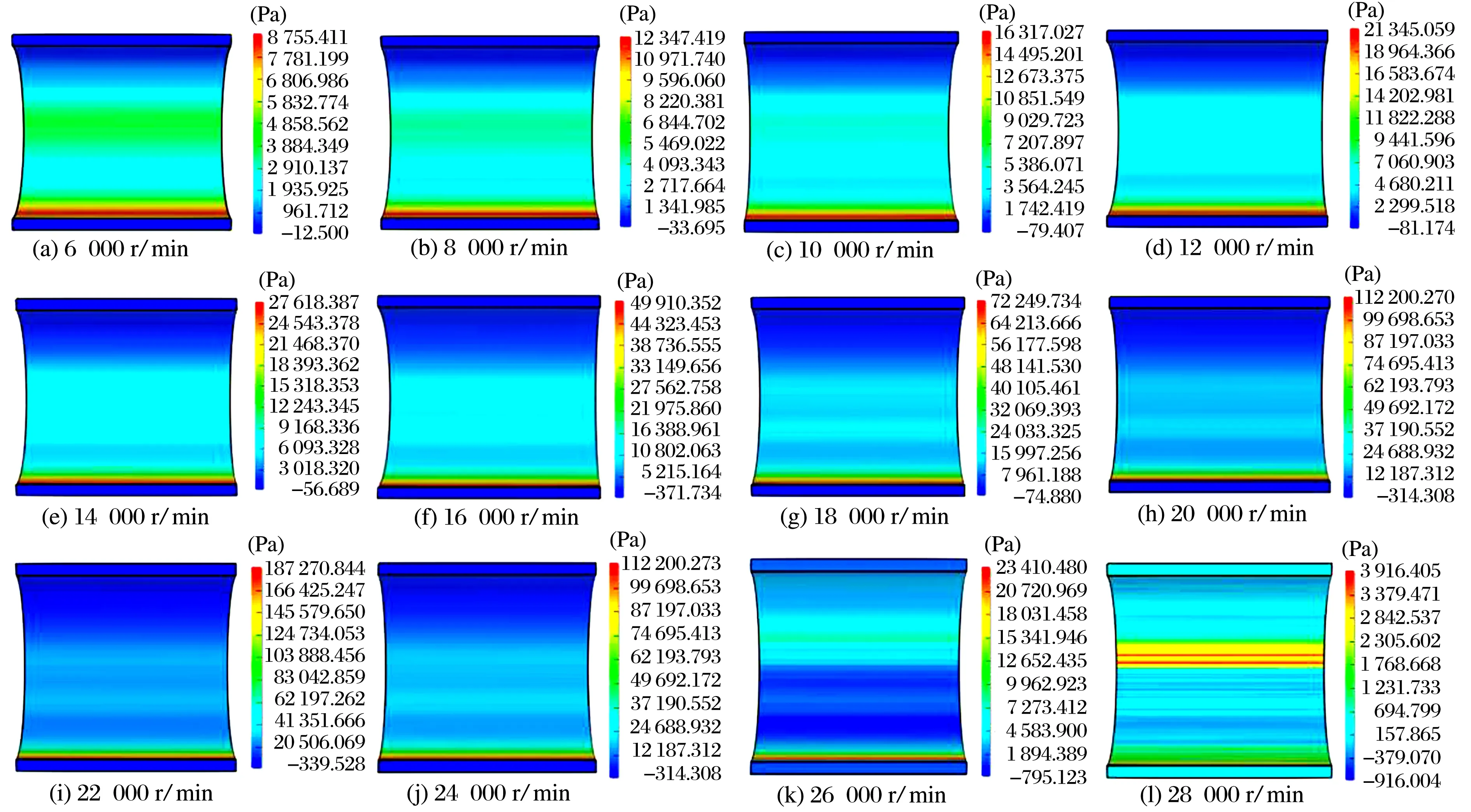
图9 光滑表面气体动压轴承气膜压力随转速的变化
由图7—图9可知:随转速增大,承载力先增大后减小,临界转速为24 000 r/min。这是由于当转速低于临界转速时,气膜速度差异较小(图8a—图8d),随转速增大,气膜压力增大(图9a—图9i),承载力增大。当转速高于临界转速时,接近瓦块壁面的一层气流碰撞瓦块后会反弹回来碰撞在转轴表面附近的气膜上,产生较大的乱流(图8e),导致稳定部分的气膜被冲散而变的不稳定,气膜压力骤降且分布不均匀(图9l),承载力减小。
在稳定状态时,箔片气体动压轴承箔片内部形成稳定气膜产生的承载力和光滑表面气体动压轴承的承载原理相同,在此与文献[15]中三代箔片气体动压轴承承载力对比以验证模型的正确性(图10),本文模型的气体动压轴承承载力仿真值与第三代箔片气体动压轴承的承载力试验值拟合曲线斜率接近。但本文模型的偏心率为0.2,适用的转速范围较低,随转速增大和偏心率变化承载力会提高,仿真结果会更贴近箔片气体动压轴承。

图10 气体动压轴承承载力仿真值与试验值对比
基于XFlow计算转速为24 000 r/min时本文模型气体动压轴承承载力随偏心率的变化规律,并与文献[3]中基于MATLAB和CFX转速为30 000 r/min时的计算结果对比,承载力随偏心率变化规律相似,进一步说明了本文模型的可行性。

图11 转速为24 000 r/min时承载力随偏心率的变化曲线
3 微织构形状和深度对气体动压轴承承载性能的影响
以第2节的气体动压轴承为例分析,偏心率为0.13。
3.1 微织构形状
微织构轴承瓦块模型如图12所示,微织构形状分别为三角形、正方形、半圆形,如图13所示,数量为17。

图12 微织构轴承瓦块模型

(a)三角形 (b)正方形 (c)半圆形
当微织构深度分别为25,50,75,100 μm时,不同微织构形状的气体动压轴承承载力随转速的变化曲线如图14所示:1)当微织构深度为25 μm时,转速为20 000 r/min附近三角形微织构轴承承载力比无微织构轴承提高约20%;2)当微织构深度为75 μm时,转速为20 000 r/min附近半圆形微织构轴承承载力比无织构轴承提高约20%,三角形、半圆形微织构轴承比无微织构轴承承载力提升约4%;3)当微织构深度为50,100 μm时,三角形、正方形、半圆形微织构轴承与无微织构轴承承载力相差不大;4)正方形微织构轴承因棱角气流碰撞而不能形成稳定的回流来改善气膜刚度,承载性能没有明显改善。

(a) 25 μm
3.2 微织构深度
微织构深度对三角形、正方形、半圆形微织构气体动压轴承承载力的影响如图15所示:当达到稳定转速20 000~24 000 r/min时,三角形微织构轴承在76 μm处承载力达到峰值474 N,正方形微织构轴承在77 μm处承载力达到峰值476 N,半圆形微织构轴承在80μm处承载力达到峰值464 N。结合3.1节分析结果可知三角形微织构气体动压轴承承载能力较好,微织构深度取76 μm左右。
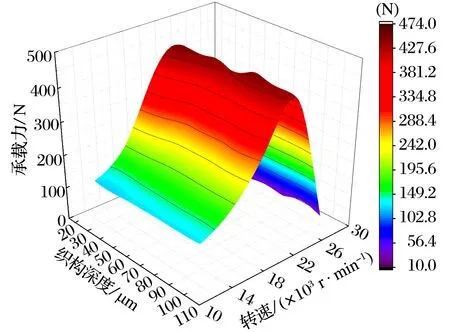
(a)三角形微织构
4 结束语
基于微观分子动力学的LBM建立气体动压轴承计算流体动力学模型,采用XFlow软件计算其承载力,并分析了微织构形状和深度对气体动压轴承承载力的影响,分析结果可以为该类轴承的设计提供参考。但本文的结果未进行试验验证,后续有待进一步研究。
