基于壳单元模型的箔片气体动压轴承静、动态特性分析

曹远龙，刘亚春，伍奕桦

(1.南华大学 a.机械工程学院；b.数理学院，湖南 衡阳 421001；2.湖南农业大学 机电工程学院，长沙 410125)

1 概述

箔片气体动压轴承依靠动压气体润滑和箔片结构的变形特性，消除了滑动轴承中的油润滑系统，获得了无油润滑、低耗能、高效率输出等优点，被广泛应用于微型燃气轮机[1]、无油涡轮增压器[2]、燃料电池空压机[3-4]、空气制冷机[5-6]等高性能机械设备中。箔片气体动压轴承由顶箔、波箔和轴承套组成，如图1所示，由于重力作用，转子偏离轴承中心，与顶箔组成收敛域和扩散域，低黏度气体被转子带入收敛域，气体转速降低产生高压气膜支承转子。波箔与顶箔和轴承套相互摩擦而具有一定的弹性刚度和阻尼，可容纳转子的大偏心振动[7-8]。

图1 箔片气体动压轴承结构示意图

然而，箔片结构变形与气膜压力的非线性关系导致预测箔片气体动压轴承的性能非常困难[9]。相关学者对如何建立有效的箔片结构模型预测轴承性能做了一定研究：文献[10]利用轴向刚度相同的刚度系数代替波箔和顶箔，忽略箔片凹陷和摩擦引起的非线性作用，建立并联刚度系数模型，耦合雷诺方程，分析了结构参数(波箔的节距、厚度、间隙等)和运动参数(转速等)对轴承动态特性系数的影响；文献[11]用若干垂直弹簧和水平弹簧等效箔片的径向刚度和周向刚度，提出了一种预测箔片气体动压轴承动态特性系数的有限元方法，分析了频率、轨道尺寸和摩擦因数的影响；文献[12]用箔片结构参数的刚度经验公式组成空间刚度矩阵，基于计算流体动力学软件求解纳维叶-斯托克斯方程，分析了箔片结构参数与轴承承载力的关系，流体膜厚度、顶箔挠度、流体压力与承载角的关系，以及负载能力与波箔和顶箔刚度的关系；文献[13]分析了顶箔的一维和二维有限元模型对箔片气体动压轴承性能的影响，顶箔二维模型中面处的最小气膜厚度预测较大，轴承两端的最小气膜厚度预测较小，顶箔一维模型能体现顶箔变形引起的周向气膜波浪形轮廓，最小气膜厚度与试验结果吻合较好，与仅考虑波箔模型相比，顶箔一维和二维模型均低估了轴承直接刚度系数和直接阻尼系数；文献[14-16]建立考虑箔片与顶箔、轴承套之间局部摩擦力的铁木辛柯梁模型，基于该模型分析发现静载荷、载荷角、滑动摩擦因数和扰动幅值对轴承刚度和阻尼系数的影响表现为非线性和各向异性，其值受接触面间滑动摩擦因数和载荷角的影响较大，给出了实现库仑阻尼和最优结构刚度的方法；文献[17-18]利用8个弹簧模拟2个节点和3个自由度的箔片变形和摩擦效应，利用能量法和卡氏定理获得每个弹簧的刚度系数，利用计算结构的动态滞回曲线验证箔片的刚度和阻尼特性；文献[19]采用2个刚性杆和1个水平弹簧等效箔片结构，提出箔片的支承刚度和结构间接触变形的Link-spring模型，分析了箔片摩擦参数、气膜间隙对轴承承载力的影响，结果表明存在最佳气膜间隙使轴承承载力最大；文献[20]基于能量法建立考虑箔片间摩擦作用、箔片平面段侧向偏转及其与轴承套分离情况的新模型，结果表明箔片平面段的横向变形会影响箔片整体变形，进而影响轴承承载力；文献[21]采用LuGre动态摩擦模型捕捉欧拉梁单元黏滑状态，分析摩擦因数和扰动量对转子系统线性和非线性稳定性的影响，结果表明摩擦因数和扰动量直接影响箔片结构的黏滑状态，转子系统非线性稳定的最优摩擦因数要高于线性稳定的最优摩擦因数。

上述箔片气体动压轴承理论模型大多假设箔片支承刚度沿轴向均匀分布，但相对集中的压力分布会使结构产生变形，进而影响箔片支承刚度。此外，箔片支承刚度轴向均匀假设不适用于其他类型的箔片气体动压轴承，如推力轴承。鉴于此，采用壳单元模拟箔片结构，考虑箔片在气膜压力作用下的凹陷和运动，以及波箔、顶箔和轴承套之间的相互作用，耦合有限差分法求解雷诺方程，建立预测箔片气体动压轴承性能的仿真分析模型，并对轴承的静、动态特性进行分析。

2 理论模型

2.1 箔片结构模型

由于气体轴承中顶箔和波箔呈现一定的弧度，且厚度远小于其长度和宽度，采用退化壳单元模拟箔片结构，退化壳单元有4个节点，每个节点有6个自由度，可以考虑壳单元的平移、转动以及横向剪切变形[20-22]，如图2所示。

图2 顶部和波箔的曲线和节点坐标

壳体内任一点的位移u，v，w可由中面上节点的3个位移uk，vk，wk以及3个转角β1k，β2k，β3k表示，其中β3k=0(即不考虑箔片面内的转动)，即

(1)

-1≤ξ≤1，-1≤η≤1，-1≤ζ≤1，

已知壳体位移函数，其空间应变分量可表示为

{εxxεyyεzzγxyγyzγzx}T=

[B1B2…Bn]{δ1δ2…δn}T，

(2)

Bk=

δk={ukvkwkβ1kβ2k}，

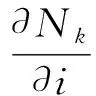
由壳单元理论可知，中面法线方向的应力始终为0[24]。局部坐标系(v1k，v2k，v3k)中的应力σ′和应变ε′的弹性关系可表示为

σ′=D′ε′，

(3)

D′ =

式中：D′为弹性矩阵；E,ν分别为材料的弹性模量和泊松比。

考虑(3)式中局部坐标系的弹性矩阵需要转换到全局坐标系矩阵下[24]，转换后的矩阵为

(4)

根据最小势能原理，单元刚度矩阵可表示为

(5)

另外，局部坐标系中的转动自由度也需要转换到全局坐标系下，用于实现单元节点刚度连接，全局坐标系下单元节点自由度可表示为

{δk}global=Trotδk′=

(6)

因此，壳单元的全局刚度矩阵可以表示为

(7)

2.2 雷诺方程

润滑气体与箔片结构的耦合过程是预测气体轴承性能的关键。顶箔与转子包围的收敛域内的气膜压力可以用雷诺方程计算[26]，即

(8)

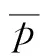
考虑箔片变形时的气膜厚度为

(9)

作用在顶箔上的载荷向量为

(10)

由于箔片的受力和变形不同，箔片在轴向和周向的摩擦力不同，可以通过集中载荷向量补充到(10)式中。

3 模型验证

以文献[19,27]的箔片气体动压轴承为例，主要结构参数见表1，顶箔和波箔的固定端垂直向上，顶箔和波箔材料为X-750。转速为30 000 r/min,载荷为134.1 N。

表1 箔片气体动压轴承的主要结构参数

箔片气体动压轴承中面处的气膜厚度预测和试验结果对比如图3所示：预测和试验结果吻合较好，验证了模型的正确性。在周向位置大于180°处出现气膜厚度最小值，且伴随波动。产生这种现象的原因为：1)气体进入收敛区，转速降低，

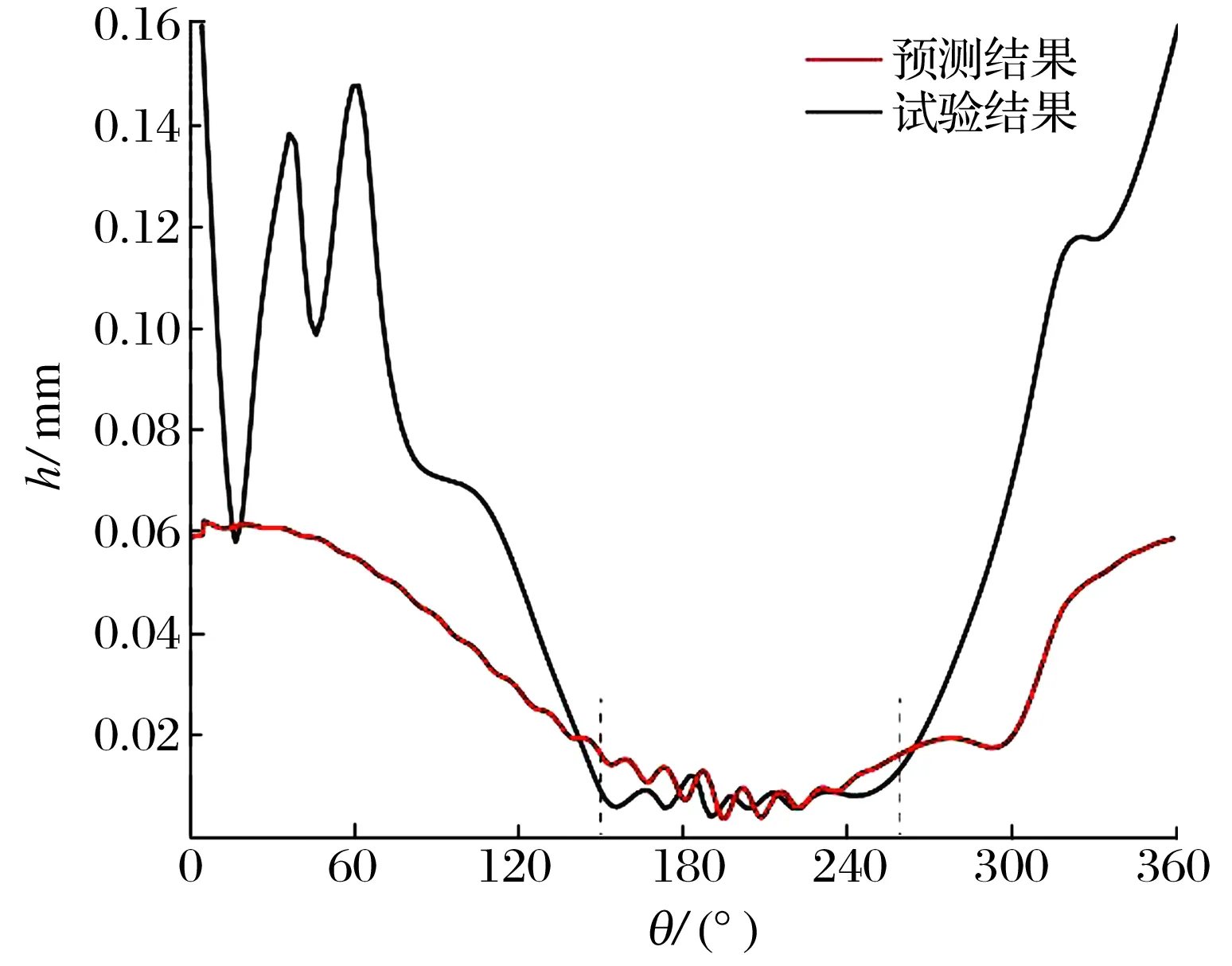
图3 箔片气体动压轴承中面处的气膜厚度

积聚并压缩气体形成高压气膜，高压气膜产生作用于转子且沿转动方向的切向力，使转子偏离载荷方向，即最小气膜厚度偏离180°；2)由于波箔凸起位置的箔片刚度大于波箔相邻凸起之间的顶箔刚度，在高压气膜作用下前者的变形小于后者，不均匀变形使气膜厚度产生波动。

4 箔片气体动压轴承静、动态特性分析

同样以第3节的箔片气体动压轴承为例分析。

4.1 静态特性

4.1.1 载荷对轴承静态特性的影响

转速为30 000 r/min，名义间隙为31.8 mm时，不同载荷下转子的偏心率和姿态角如图4所示：随载荷增大，姿态角减小，偏心率增大。这是由于随载荷增大，可压缩性气体只有减小体积才能提高气膜压力以支承转子载荷沿姿态角方向和垂直姿态角方向的分力，使转子远离轴承中心，并沿载荷方向移动。

图4 载荷对转子偏心率和姿态角的影响

4.1.2 转速对轴承静态特性的影响

载荷为10 N，名义间隙为31.8 mm时，不同转速下转子的偏心率和姿态角如图5所示： 两者均随转速升高而减小。这是由于转速升高时单位时间内更多的气体进入收敛域，形成较大的动压效应，提高了气膜刚度，使转子向轴承中心移动，转子移动会使气膜间隙增大，降低高压域内的气膜压力，进而减弱气膜对转子的切向作用力。

图5 转速对转子偏心率和姿态角的影响

4.1.3 长径比对轴承静态特性的影响

转速为30 000 r/min，载荷为10 N，轴承直径为38.1 mm时，不同长径比(轴承长度与直径的比值)下转子的偏心率和姿态角如图6所示：随长径比增大，偏心率减小，姿态角增大，说明转子向轴承中心移动。这是由于长径比增大(增大轴承长度)，使气膜的高压域范围增大，既提高了气膜支承转子的作用力，又提高了气膜切向力，推动转子沿转动方向偏移。

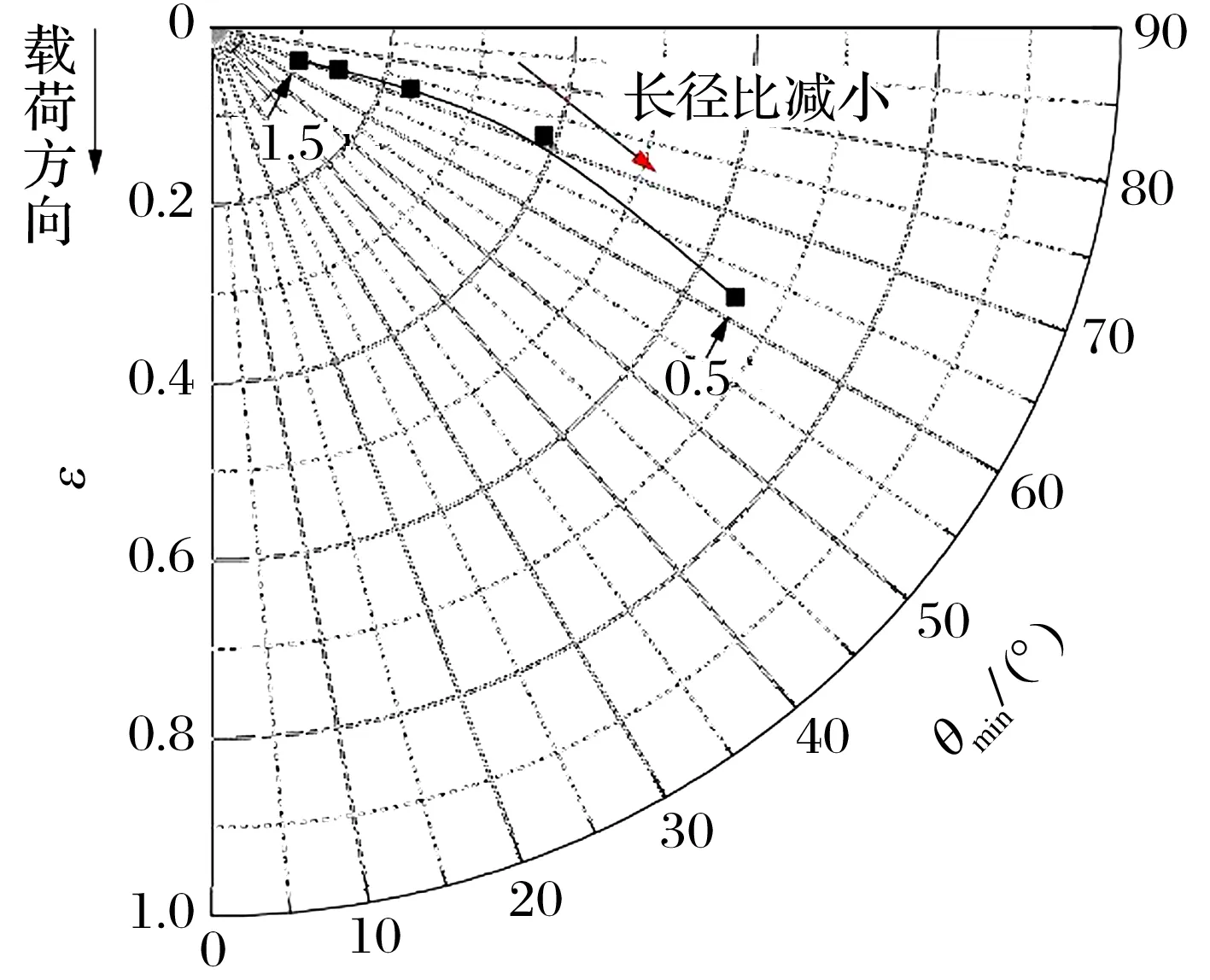
图6 轴承长径比对转子偏心率和姿态角的影响

4.1.4 气膜间隙比对轴承静态特性的影响

转速为30 000 r/min，载荷为10 N，名义间隙为38.1 mm时，不同间隙比(计算间隙与名义间隙的比值)下转子的偏心率和姿态角如图7所示：两者均随间隙比增大而增大，间隙比较小时，转子接近轴承中心。这是由于小间隙比时可以产生较大的气膜刚度，减小了转子偏移。此外， 小间隙比会使气膜厚度沿周向均匀分布，转子所受切向力减小，转子接近轴承中心。随间隙比增大，高压域面积减小，气膜刚度减小，转子远离轴承中心。

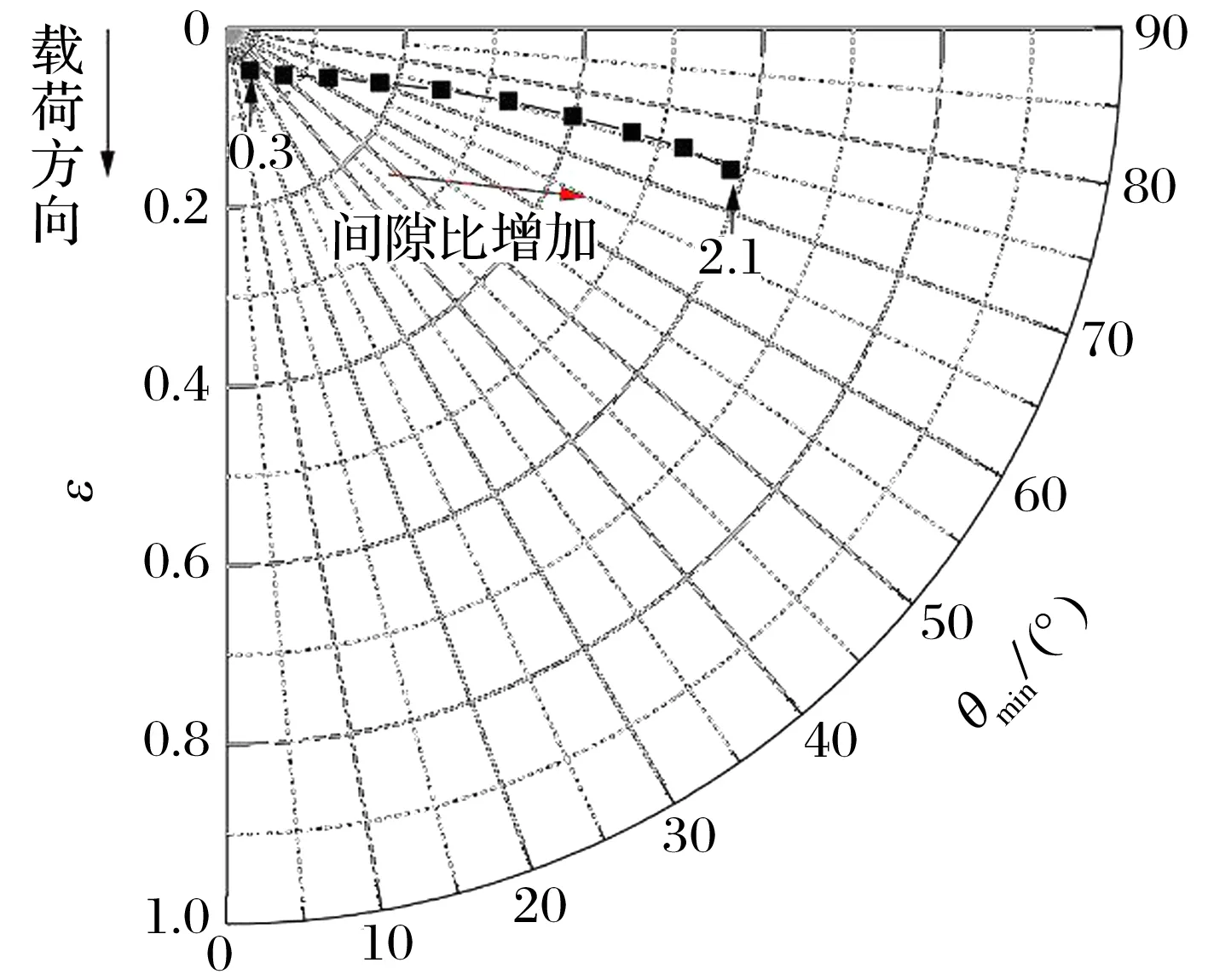
图7 间隙比对转子偏心率和姿态角的影响

4.2 动态特性

4.2.1 载荷对轴承动态特性的影响

转速为30 000 r/min,名义间隙为31.8 mm时，不同载荷下的箔片气体动压轴承动态特性系数如图8所示：1)随载荷增大，动态直接刚度系数明显增大，尤其是x方向，这是由于沿x，y方向的力Fx，Fy随载荷增大而增大，且Fx增大明显，这些力迫使偏移的转子与顶箔之间形成明显的收敛域，提高了气膜压力，使轴承动态刚度系数增大；2)大载荷时较大的气膜压力会使箔片产生局部变形，形成多个气膜压力波峰，降低了轴承动态直接阻尼系数Cxx；3)2个交叉刚度系数略有增加，差值(Kxx-Kyy)先减小后增大。动态直接阻尼系数减小和(Kxx-Kyy)增大会使系统能耗降低，转子运行不稳定。

图8 载荷对轴承动态特性系数的影响

4.2.2 波箔凸起周向间隔角对轴承动态特性的影响

转速为30 000 r/min，名义间隙为38.1 mm时，不同波箔凸起周向间隔角(相邻凸起的夹角)下的箔片气体动压轴承动态特性系数如图9所示：1)动态刚度系数几乎不受周向间隔角影响；2)动态阻尼系数在低载荷下几乎不受周向间隔角影响，在高载荷下受周向间隔角的影响,这是因为在低载荷时气膜压力稳定，在高载荷时由于结构变形气膜压力波动较大。

图9 波箔凸起周向间隔角对轴承动态特性系数的 影响

4.2.3 顶箔、波箔厚度对轴承动态特性的影响

转速为30 000 r/min，载荷为10 N时，不同顶箔、波箔厚度下的箔片气体动压轴承动态特性系数见表2：动态刚度系数和动态阻尼系数随顶箔、波箔厚度变化不明显。结合图9可知：对于具有一定结构刚度的箔片轴承，经气膜离散的低载荷不会引起箔片结构变形，改变箔片数量和厚度对气膜分布无影响；大载荷时，选择合适的箔片数量和厚度可以改善轴承动态特性。

表2 不同顶箔、波箔厚度下的轴承动态特性系数

4.2.4 长径比对轴承动态特性的影响

转速为30 000 r/min，载荷为10 N，名义间隙为38.1 mm时，不同长径比下的箔片气体动压轴承动态特性系数如图10所示：随长径比增大，动态直接刚度系数和动态直接阻尼系数明显增大，交叉刚度系数减小，交叉刚度的差值(Kxy-Kyx)基本不变。说明长径比增大可以改善气膜的轴向分布，并容纳更多的气体来“硬化”轴承。大长径比的轴承动态直接阻尼系数的增大说明消耗转子振动的能力增强，有利于系统稳定；但转子高速运转时可能会产生圆锥形模态振动，大长径比的箔片结构将增加转子和轴承边缘碰撞的可能性。

图10 长径比对轴承动态特性系数的影响

4.2.5 气膜间隙比对轴承动态特性的影响

转速为30 000 r/min，载荷为10 N，名义间隙为38.1 mm时，不同间隙比下的箔片气体动压轴承动态特性系数如图11所示：1)随间隙比增大，动态直接刚度系数和动态直接阻尼系数快速下降，最终趋于稳定,说明气膜间隙增大将使轴承变“软”，消耗振动的能力减弱；2)当间隙比较小时，动态刚度系数和动态阻尼系数较大，特别是当间隙比小于0.7时，交叉刚度系数的差值(Kxy-Kyx)为负，此时动态阻尼和(Kxy-Kyx)的耗能为正数，有利于系统的稳定性[26]，但小气膜间隙的轴承会导致起飞过程中的起飞扭矩和速度增大。

图11 间隙比对轴承动态特性系数的影响

5 结论

采用壳单元模拟箔片结构，考虑箔片在气膜压力下的凹陷和运动，以及波箔、顶箔和轴承套之间的相互作用，建立预测箔片气体动压轴承性能的仿真分析模型，耦合有限差分法求解雷诺方程，分析了轴承的静、动态特性，得出以下结论：

1)载荷增大会使转子远离轴承中心，大负载转子的运动状态变化需要更多的能量，适当增加载荷可以提高轴承稳定性；

2)转速增大会使转子向轴承中心移动，转速越大，转子振动越大，越不稳定；

3)在低载荷下改变箔片数量和厚度对轴承性能影响不大；

4)可以通过优化气膜间隙改善轴承性能，存在一个最优气膜间隙使轴承承载力最佳，但小气膜间隙会导致起飞过程中的起飞扭矩和速度增大，应慎重选择。