箔片气体动压轴承力学建模研究进展
2022-10-21李长林杜建军李洁徐珍妮
李长林,杜建军,李洁,徐珍妮
(哈尔滨工业大学(深圳) 机电工程与自动化学院,广东 深圳 518055)
1 概述
近年来节能减排和绿色低碳成为主流的发展趋势,提高能源动力装备的能源转化效率是重要实现途径之一。氢燃料电池空压机、微型燃气轮机等高速旋转机械已显示出巨大的应用前景,轴承是旋转机械的核心部件,是整机高速稳定运转的重要基础。滚动轴承与油膜滑动轴承有较高的承载能力,受dn值、寿命、润滑条件与运行环境的影响,一定程度上限制了其在高温、高速旋转机械中的应用。
箔片气体动压轴承是一种自作用式的被动控制轴承,通常由形成润滑气膜的平箔片与具有弹性支承作用的底层箔片组成。箔片轴承的动压气膜与箔片结构串联支承转子,可同时实现动压气体润滑与柔性支承。动压气膜的摩擦力矩较低,可以有效降低能耗。弹性箔片变形使箔片轴承具有较好的转子不对中适应性,高温条件下的热膨胀适应性与抗冲击能力。箔片结构在发生弹性变形的同时,内部的库仑摩擦效应为箔片轴承提供库仑阻尼,提升了支承转子的高速稳定性,使箔片气体轴承能达到较高的dn值。
最早应用的箔片气体动压轴承为第一代波箔型与悬臂型轴承,如图1所示,前者通过连续波拱形结构支承顶箔片,后者的圆弧形悬臂箔片依次搭接形成收敛隙与弹性支承结构。相比悬臂型轴承,波箔型轴承的承载力与刚度较大;但悬臂型轴承具有多流场与预紧效应的特点,较适合高速轻载工况。

图1 波箔型与悬臂型箔片轴承结构示意图
第二代波箔轴承在某一个轴向、周向或径向采用波箔结构的变刚度设计,第三代波箔轴承同时在轴向与周向进行变刚度设计。第二代悬臂箔片轴承具有底层弹性支承,也可以进行周向变刚度设计。改进后2种类型轴承的静、动态性能均得到了较大提升[1]。
其他有代表性的箔片轴承有多滑动梁型[2-4]、金属丝网型[5]、嵌套弹簧型[6]径向箔片轴承,三者均具有较好的动态性能。止推箔片轴承有层叠型[7-8]、鼓泡型[9]等,具有较好的二维刚度设计性。近年来,也有学者提出了主动控制气膜间隙的新型箔片轴承以提升轴承动态性能[10]。
箔片气体动压轴承的性能很大程度上取决于弹性箔片结构的力学特性。在箔片结构间接触/分离、库仑摩擦引起的静止/滑动等复杂接触约束的影响下,箔片轴承的理论研究具有较大难度。而建立箔片轴承的箔片结构力学模型是进行理论研究的第一步,力学模型的准确和完备程度对箔片轴承性能预测的准确性有重要影响。完备的多维箔片结构力学模型,考虑轴承内部不同类型的接触约束,研究真实微动摩擦作用下的库仑阻尼效应,能够更加准确地预测复杂箔片结构轴承的支承性能。
2 波箔气体动压轴承的力学建模
2.1 波箔结构采用线性弹簧建模
国外学者最先基于简化的箔片结构模型对波箔式气体动压轴承开展研究。文献[11]建立了波箔结构的力学模型,推导了单个波箔刚度的计算公式,但忽略了波箔之间的相互作用以及平箔片与波箔片之间的摩擦力,波箔被简化为线性弹簧。文献[12]结合波箔的线性弹簧模型与流体动压润滑理论,研究了波箔刚度、转子转速等因素对轴承承载力的影响,发现减小箔片刚度会降低轴承承载力,但相同最小气膜厚度条件下箔片刚度较小时的轴承承载力较大;增加平箔片数(流场数)也会降低轴承的承载力,但摩擦力矩在平箔片数为3时较小。文献[13]提出了简化波箔结构的新刚度计算模型,推导了固定端与滑动端波箔对应的刚度计算公式,同时考虑了波箔与轴承套之间的摩擦力作用。文献[14]利用线性弹簧模型简化波箔结构并计算了轴承的静态特性,结果表明最小气膜厚度相同条件下,箔片变形使箔片轴承高压区分布面积比刚性轴承大,轴承承载力也相应较大;与刚性轴承相比,箔片轴承支承转子的姿态角较小,高速稳定性较好。文献[15]分别采用一维梁单元与二维薄壳单元对平箔进行有限元建模,并采用文献[13]提出的模型计算波箔刚度,研究表明,基于一维梁平箔片模型计算的最小气膜厚度和转子姿态角更接近试验值,基于二维薄壳平箔片模型在轴承宽度的中间区域计算所得气膜厚度值较大,在轴承端部计算所得气膜厚度较小。以上波箔结构模型均被简化为线性弹簧,并没有考虑波箔之间的相互作用以及多个波箔在库仑摩擦力作用下的“静止-滑动”状态。
2.2 波箔结构采用梁模型建模
有学者在简化波箔模型的基础上,建立有摩擦的带状波箔力学模型。文献[16]建立了带状波箔的力学模型,考虑了波箔片与轴承套、平箔片间的摩擦力以及波箔之间的相互作用,研究了周向载荷分布和波箔结构参数对箔片刚度的影响规律,结果表明,增大波箔与轴套间的摩擦因数会使更多的波箔处于静止状态而无法滑动,增大了整体箔片结构刚度,降低了库仑摩擦耗能;但增大平箔与波箔之间的摩擦因数对波箔的滑动影响较小,能更有效地增大箔片结构的库仑阻尼。文献[17]用3个线性弹簧等效替代每个波箔,基于波箔实际尺寸与卡式第二定理计算各弹簧刚度,考虑了波箔间的相互作用以及各接触面上摩擦力,建立了带状波箔的多自由度力学模型,如图2a所示;轴承静态加载的计算结果与有限元软件仿真结果以及试验结果均比较接近,该研究也发现波箔之间的相互作用会增大波箔片的刚度。文献[18]将波箔结构等效为2个刚性杆并通过线性弹簧连接,水平连接段也等效为刚性杆,建立了波箔结构的link-spring模型与平箔片的有限元壳模型,如图2b所示;基于卡式定理推导了连接弹簧刚度,在考虑波箔之间的相互作用、各接触面的摩擦力以及平箔变形的基础上分析了名义间隙对轴承承载力的影响。

(a)多自由度模型
文献[19]基于梁理论建立了波箔结构的有限元模型来研究摩擦力对波箔轴承静态特性的影响,波箔结构采用空间直梁单元搭建而成,并提出了判断波箔带各波箔“静止-滑动”状态的计算流程,进行了轴承加卸载过程仿真;研究表明增大摩擦因数会增加处于静止状态的波箔数目,减小轴承加卸载曲线的包围面积,此时轴承特性与刚性轴承逐渐接近。文献[20]分别基于梁理论与有限元商业软件建立了波箔结构力学模型,研究表明波箔两端的弯曲力矩对箔片结构刚度影响较大,通过减小波箔展角、减少波箔数量、减小接触面摩擦因数或改变载荷分布形式能够让更多的波箔参与滑动。文献[21]同样采用多个空间直梁搭建波箔结构力学模型,考虑了轴承结构之间的库仑摩擦力,相邻波箔之间的相互作用与波箔的周向滑动,并计算了不同载荷分布作用下波箔的变形与滑动情况。
上述基于梁模型构建波箔力学模型的研究是基于传统的单层波箔结构,文献[22]则基于link-spring模型对双层波箔轴承进行了理论建模、计算分析与试验研究,其设计并制造了多种不同间隙的双层波箔,探究结构参数对轴承性能的影响,对比分析单层和双层波箔刚度及阻尼特性的差异。文献[23]基于接触力学与曲梁单元建立了双层波箔与平箔结构的力学模型(图3),其考虑了平箔片与第1层波箔之间,两层波箔之间,底层波箔与轴套之间的法向及切向接触约束,计算得到了库仑摩擦效应影响下双层波箔轴承的非线性刚度特性。

图3 双层波箔接触间隙与曲梁有限元模型
也有学者通过商业软件与接触力学建立波箔轴承制造误差分析模型,研究制造误差对轴承静态特性的影响。文献[24]基于ABAQUS对波箔轴承进行建模,仿真了静态转子的加卸载,研究了波箔高度、节距与曲率半径制造误差对波箔刚度的影响规律;研究发现波箔高度制造误差对箔片结构的刚度影响最大,波箔高度的一致性误差达到20 μm时,整体箔片刚度将下降40%。文献[25]基于文献[17]中的多自由度波箔结构模型,应用接触力学对轴承内部接触约束进行了建模,仿真了静态转子加载过程中波箔的摩擦滑动与相邻结构间的“接触-分离”状态,也研究了波箔高度制造误差对结构特性的影响规律;在其基础上,考虑转子在起飞过程中与顶箔的接触状态变化,建立了波箔轴承转子起飞过程的计算模型[26]。
文献[27]通过非线性梁理论对有预紧的三叶顶箔与波箔片进行建模,考虑了大曲率半径箔片结构装配过程中的大变形,但很少有关于该研究建模与公式推导过程的介绍。
2.3 波箔结构采用壳模型建模
基于梁理论建立的波箔结构模型只能计算带状波箔沿周向的一维变形分布,而不能计算沿轴向的变形分布。文献[28]考虑了三维波箔结构,基于含有拉伸与弯曲应变的板单元建立了带状波箔力学模型,研究表明波箔间的连接段有助于增加轴向的箔片变形一致性,而采用线性弹簧模型的计算结果则高估了高压区的气膜厚度,同时也低估了轴承两端的厚度值。文献[29]基于有限元法采用4节点MITC 壳单元建立了波箔与顶箔的三维结构力学模型,考虑了接触面的库仑摩擦力,计算了转子不对中条件下的轴承静态特性。文献[30]也基于有限元法与接触力学建立了轴向多条波箔带且变刚度分布的第二代波箔轴承力学模型,研究表明轴向变刚度的波箔轴承在转子不对中条件下具有更高的承载能力。
3 悬臂气体动压轴承力学建模
悬臂型箔片轴承从20世纪70年代开始就成功应用在飞机的空气循环机上,但相关的参考文献与技术材料较少,一个重要原因是这种相互搭接的箔片结构建模难度较大。尽管如此,一些专家仍然致力于该类轴承的研究并取得了一定的研究成果。文献[31]用悬臂箔片轴承代替滚动轴承进行了一系列的涡轮发动机试验,结果证明了悬臂箔片轴承在军用发动机中应用的可能性。在之后的项目中,文献[32]提出了悬臂型箔片轴承的分析模型,分别给出了箔片结构变形与气弹耦合的计算框架,而且计算结果与试验结果较为一致。文献[33]在对相互搭接的箔片结构进行建模时,采用位移相关方程对每个接触节点的位移进行约束,并研究了相邻搭接的箔片之间,转子与箔片之间的摩擦力对轴承承载力的影响,文献[34]则进一步考虑了箔片之间的面接触约束与轴承套的约束,增加了模型的完整性。文献[35]采用有限元法仿真计算了悬臂箔片的变形,包括径向、切向节点位移与节点转角,模型假设了箔片与轴套间的单方向转动刚度,但其建模方法的介绍不够详细。
文献[36]仿真了波箔片支承的悬臂式箔片轴承的装配过程,证实了利用辅助仿真单元装配轴承的可能性。文献[37]则引入接触力学研究了波箔轴承的平箔片与波箔片之间的接触问题,结果表明直接接触法在研究箔片轴承中的接触问题时较为合适。文献[38]研究了搭接箔片之间的面接触(图4)对悬臂箔片轴承静态特性的影响,研究发现相邻箔片之间面接触效应会增大箔片结构刚度,进而提高轴承的承载力。文献[39]则基于接触力学建立了悬臂箔片轴承内部全面的接触约束模型,包括相邻箔片之间的面接触约束,各箔片与轴承套间的接触约束以及转子与箔片之间的接触约束,结果表明轴承套对各箔片的约束进一步增大了轴承承载力。

图4 悬臂箔片间面接触效应示意图
4 其他类型箔片轴承力学建模
湖南大学冯凯团队针对不同类型的新型箔片轴承开展研究:基于梁理论,针对叠片式止推箔片轴承与三瓣式径向箔片轴承进行了力学建模[3,8],研究了轴承的静动态特性;对金属丝网箔片轴承进行了力学建模,将金属网结构划分为多层结构,每层均由许多弹性微单元结构组成[5],每个微单元可以用存在干摩擦且相互作用的曲梁结构建模(图5),理论计算与试验结果较为一致;将金属丝网结构与波箔结构相结合,提出了二者共同作为底层支承结构的新型箔片轴承[40-41],该轴承克服了金属网轴承装配精度低,寿命短的缺点,同时具有波箔轴承刚度大的优点;对嵌套压缩弹簧支承的新型箔片轴承进行了理论建模与试验研究[6],采用卡式定理计算了弹簧的刚度,同时也考虑了相邻弹簧间的摩擦力与弹簧的轴向刚度,理论计算的结构刚度与试验结果相近;近期提出了一种新型主动控制箔片轴承,采用压电作动器与杠杆放大结构控制气膜间隙分布[10],研究了驱动电压对气膜压力、转子偏心及启动力矩的影响,也研究了主动控制对轴承的动态特性的影响,结果表明主动控制后的轴承主刚度与交叉刚度差值较大,转子稳定性较好;另外,还提出了一种记忆合金驱动主动控制箔片轴承,可以对箔片轴承刚度、阻尼进行主动控制[42]。
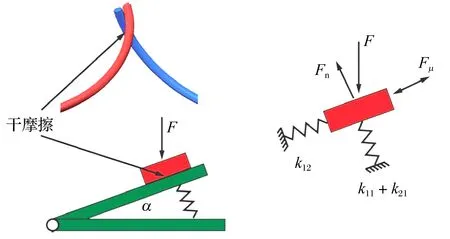
图5 金属丝网微单元等效刚度模型
哈尔滨工业大学(深圳)杜建军团队基于有限元薄板理论与接触力学建立了层叠式止推箔片轴承的层板接触力学模型,求解了层板间接触、分离状态与协调变形问题,分析了该轴承的承载机理[7];也针对滑动梁径向箔片轴承建立了多接触约束力学模型,根据滑动梁结构竖直与水平位移耦合的原理,采用非线性欧拉梁单元建模,同时采用矩形板单元对顶箔建模,还考虑了两端自由滑动梁在轴承套表面有摩擦滑动以及平箔片与多滑动梁之间的面接触效应,研究了该类型轴承的静态特性与承载机理[4]。
另外,文献[9]提出了一种双层鼓泡止推箔片轴承,基于有限元法建立了该轴承的力学模型并研究了双层鼓泡位置优化对轴承承载力的影响;文献[43]基于有限差分法与有限元法求解了表面刻微槽结构的箔片轴承的静动态特性,结果表明平箔片表面刻微槽能够减少轴承端泄,并提高轴承承载力与刚度。
5 总结与展望
对国内外箔片气体动压轴承的力学建模研究进展进行了归纳总结,发现大部分研究都是针对第一代波箔轴承,波箔结构建模从忽略库仑摩擦效应的简化线性弹簧模型逐渐发展到考虑波箔真实三维形状与库仑摩擦效应的完备有限元模型。也有文献建模研究了箔片变形方向具有非线性刚度的双层波箔轴承、轴向变刚度的第二代波箔轴承、三叶有预紧波箔轴承,以及采用接触力学计算方法的波箔高度制造误差影响研究与转子起飞过程仿真。
针对悬臂型箔片轴承的研究相对较少,其力学模型也经历了从简单到完备的发展过程,逐渐考虑相邻箔片之间的面接触效应、转子与箔片间的“刚-柔”接触装配预紧效应以及轴承套对悬臂箔片的刚性支承效应。
除了波箔型与悬臂型箔片轴承,也有相关文献针对金属丝网式、嵌套弹簧式、鼓泡式、层叠式、多滑动梁式箔片轴承建立力学模型进行研究;也有学者对主动控制式箔片轴承进行研究,通过对气膜间隙、箔片结构刚度阻尼的主动控制以提高箔片轴承的高速稳定性。
总的来说,更多类型箔片轴承逐渐被研究,轴承性能逐渐被熟知。从箔片轴承力学建模方法发展趋势来看,通过结构有限元法与接触力学数值算法的有机结合,能够对更加复杂且包含非线性接触约束的箔片结构进行精细建模,从而计算得到更准确的箔片轴承性能参数,例如非线性刚度、阻尼特性与箔片结构制造误差的影响效应等。
目前,不同类型箔片轴承的力学建模方法仍存在一些不足:波箔型箔片轴承力学建模发展比较完善,但仍然存在小偏心或小载荷条件下理论计算与试验结果之间误差较大的问题;还未有相关力学模型研究悬臂型箔片轴承的库仑摩擦耗能特性以及箔片装配过程中的大变形效应;其他类型箔片轴承的力学模型大多过于简化,没有考虑实际结构形状、库仑摩擦等因素。这些不足之处还需要完善力学模型并进行更深入的研究:建立考虑箔片制造成形误差的模型来提高理论与试验结果之间的一致性;基于接触力学与线性、非线性有限元法的建模方法在不同类型箔片轴承研究中较强的实用性与较高的准确性,将该方法应用到不同类型箔片轴承的动特性与热特性研究中。
