波纹型止推箔片轴承静态特性分析
2022-10-21侯留凯郝开元
侯留凯,郝开元
(北京航天动力研究所,北京 100076)
相对于传统轴承,气体轴承具有寿命长,工作转速高,工作温度范围广,摩擦损耗低,几乎无需维护等诸多优点[1-5],应用于深空探测发电装置、飞机空气循环机、污水处理厂曝气风机、氢燃料电池空压机、微型燃气轮机之中。
波纹型止推箔片轴承(以下简称止推箔片轴承)是研究最多,应用最广的一种气体轴承[6-13]:文献[14]建立了将波箔结构等效为弹簧结构的模型,分析了箔片轴承的特性;文献[15]研究了箔片摩擦因数和波纹数量对波纹箔片刚度的影响规律;文献[16]建立了考虑波纹结构摩擦的刚度计算模型,推导了自由端和固定端的波箔刚度方程,仿真结果与试验结果的趋势比较吻合;文献[17]采用有限元法和有限差分法耦合的新方式求解雷诺方程, 计算了止推箔片轴承的压力分布和承载力;文献[18]对止推箔片轴承的承载性能进行研究,发现合理设计波纹支承结构可以减小顶箔变形,进而提升其承载力;文献[19]得到了楔形高度对轴承承载力和刚度阻尼的影响规律;文献[20]发现存在一个最佳楔形高度,使箔片轴承有最佳的工作效率。
上述文献大多从个别参数对止推箔片轴承静态特性(承载力、摩擦力矩)进行分析,鲜有全面分析轴承结构参数对静态特性影响的文献;而且,与传统轴承相比,止推箔片轴承的承载力较低:因此,对止推箔片轴承的静态特性进行研究,得到轴承各结构参数对轴承特性的影响关系具有较强的工程意义,可为止推箔片轴承的优化设计提供一些参考。
1 理论分析
1.1 轴承结构
止推箔片轴承基于流体动压润滑原理进行工作,结构并不复杂,主要由平箔片、波纹箔片和底板组成。
止推箔片轴承单个扇形瓦块的结构如图1所示。瓦块的角度被称为扇形瓦块张角β,瓦块的倾斜区域被称为楔形区域,平坦区域被称为非楔形区域。楔形区域占整个扇形瓦块的比例被称为轴承的节距比b,底板与平箔片的非楔形区域高度差被称为楔形高度δh,推力盘与平箔片之间的最小间隙称为最小气膜厚度C。

图1 止推箔片轴承单个扇形瓦块的结构
1.2 控制方程
本文进行以下假设:
1)轴承与推力盘之间为平行状态,即不考虑推力盘的倾斜效应;
2)气膜厚度与轴承径向、周向尺寸相比很小,压力在气膜厚度方向上保持一致,不发生变化;
3)气体为绝热的理想气体,遵守理想气体定律方程。
基于以上假设,轴承的雷诺控制方程为
(1)
式中:r为径向方向坐标;h为气膜厚度;p为气膜压力;θ为周向坐标;μ为气体黏度;ω为旋转角速度。
1.3 气膜厚度与箔片变形方程
雷诺方程中的气膜厚度h可以表示为
h=C+g(r,θ)+w(r,θ),
(2)
(3)
式中:C为推力盘与轴承之间的最小气膜厚度;g(r,θ)为楔形区域与非楔形区域之间气膜厚度的变化量;w(r,θ)为箔片在压力作用下的变形量。
箔片变形量w(r,θ)需利用箔片的刚度模型求解,本文将波纹箔片等效为线性弹簧模型,忽略平箔片刚度以及箔片与底板、平箔片之间的摩擦力,箔片的结构如图2所示,其刚度计算公式为
(4)
式中:E为箔片材料的弹性模量;t为箔片厚度;s为单个箔片的长度;l为圆周方向半波箔长度;υ为箔片材料的泊松比。

图2 波箔结构
采用上述刚度计算模型,推力盘与轴承之间的量纲一的气膜厚度可以表示为
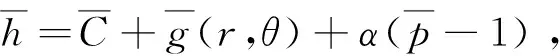
(5)
(6)
式中:α为箔片柔度变形系数,与箔片刚度K成反比关系;pa为环境压力。
1.4 边界条件与方程求解

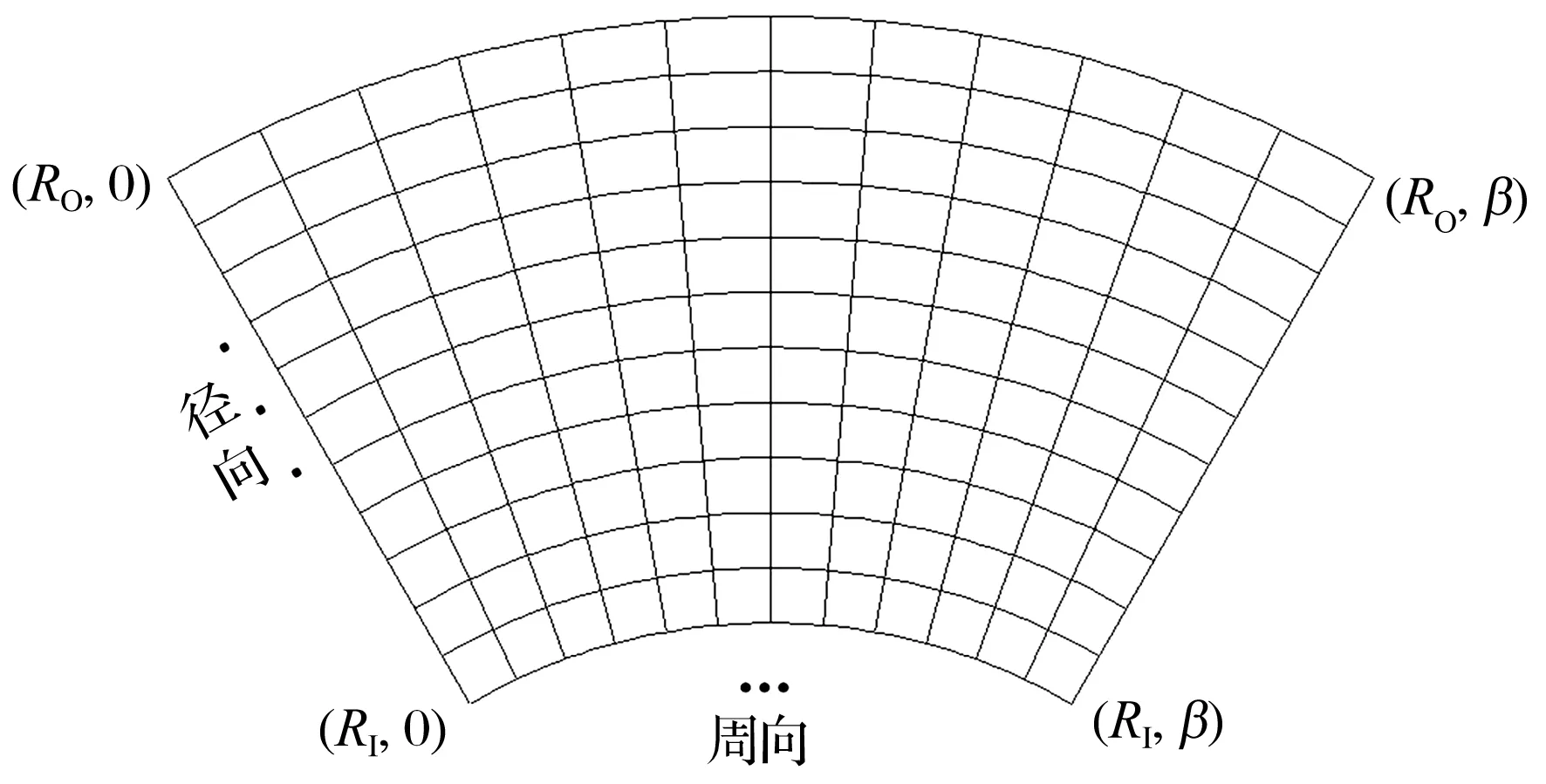
图3 网格划分示意图

图4 网格数量无关性验证
本文采用Fortran语言编程,程序逻辑结构如图5所示,当压力和气膜厚度满足收敛条件,输入计算结果。其中,止推箔片轴承的静态特性主要包括轴承承载力和摩擦力矩[21],分别为
(7)
(8)
式中:N为扇形瓦块数;W为轴承承载力;RO为轴承外径;RI为轴承内径;T为轴承摩擦力矩;Λ为轴承数。

图5 止推箔片轴承静态特性求解流程图
采用文献[13]的计算参数,根据编写的计算程序计算不同箔片变形柔度系数α和不同转速n下的轴承承载力W,结果见表1:承载力随箔片柔度系数的增大不断减小,随转速的增大不断增大,计算结果的误差均不超过2.5%,说明编写的程序正确、合理。
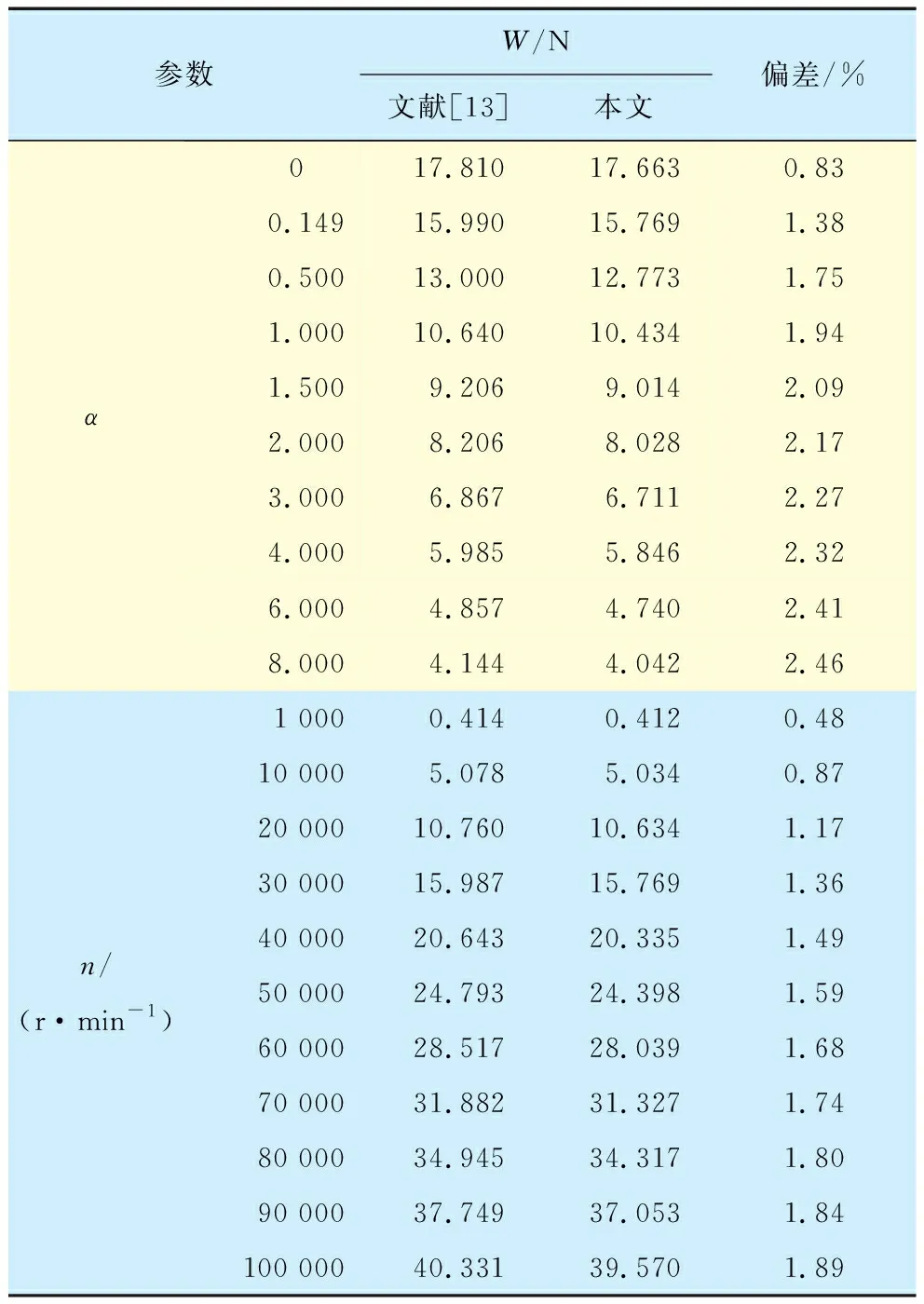
表1 止推箔片轴承承载力计算结果
2 仿真优化分析
止推箔片轴承的结构参数见表2,对其进行仿真分析,得到轴承承载力和摩擦力矩随最小气膜厚度的变化关系如图6所示,轴承承载力和摩擦力矩均随着气膜厚度的增加而不断降低,且变化较为明显。最小气膜厚度8 μm时,止推箔片轴承量纲一的压力P的分布如图7所示,压力分布较大的地方为轴承非楔形区域,也是轴承的主承载区(压力分布图的右侧为非楔形区域)。

表2 止推箔片轴承结构参数

图6 承载力和摩擦力矩随最小气膜厚度的变化
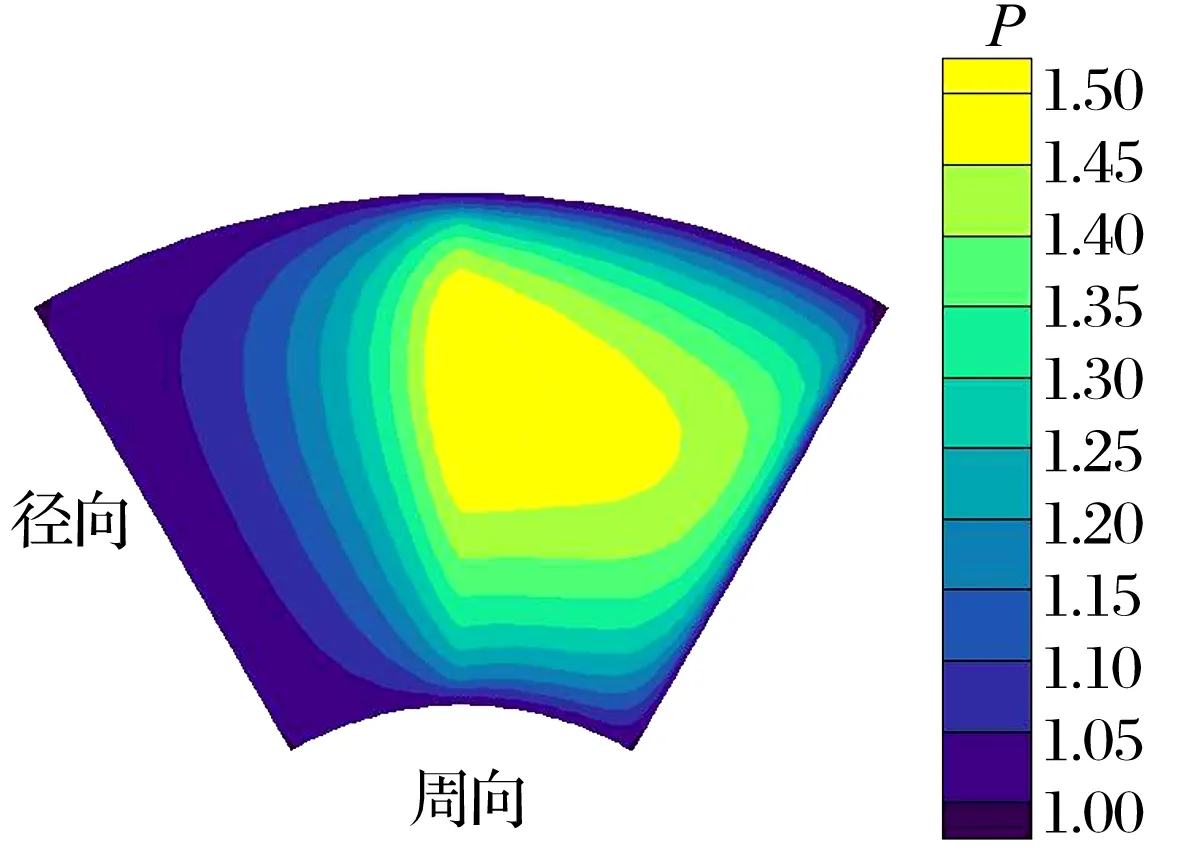
图7 止推箔片轴承量纲一的压力云图(C=8 μm)
2.1 节距比的影响
基于表2的计算参数,改变轴承节距比,得到轴承承载力及摩擦力矩随节距比的变化关系,扇形瓦块中线沿周向的压力分布以及轴承量纲一的压力云图,结果如图8—图10所示:随着节距比的增加,轴承承载力呈先增大后减小的趋势,摩擦力矩不断减小;沿周向的压力最大值始终出现在楔形区域与非楔形区域的交界处;随着节距比的增加,非楔形区域的压力值更大、更陡峭,但压力较高区域的面积占比越来越小;在节距比为0.5时,轴承承载力较大且瓦块的压力分布较平坦,可认为此时轴承的承载能力最优。

图8 承载力和摩擦力矩随节距比的变化
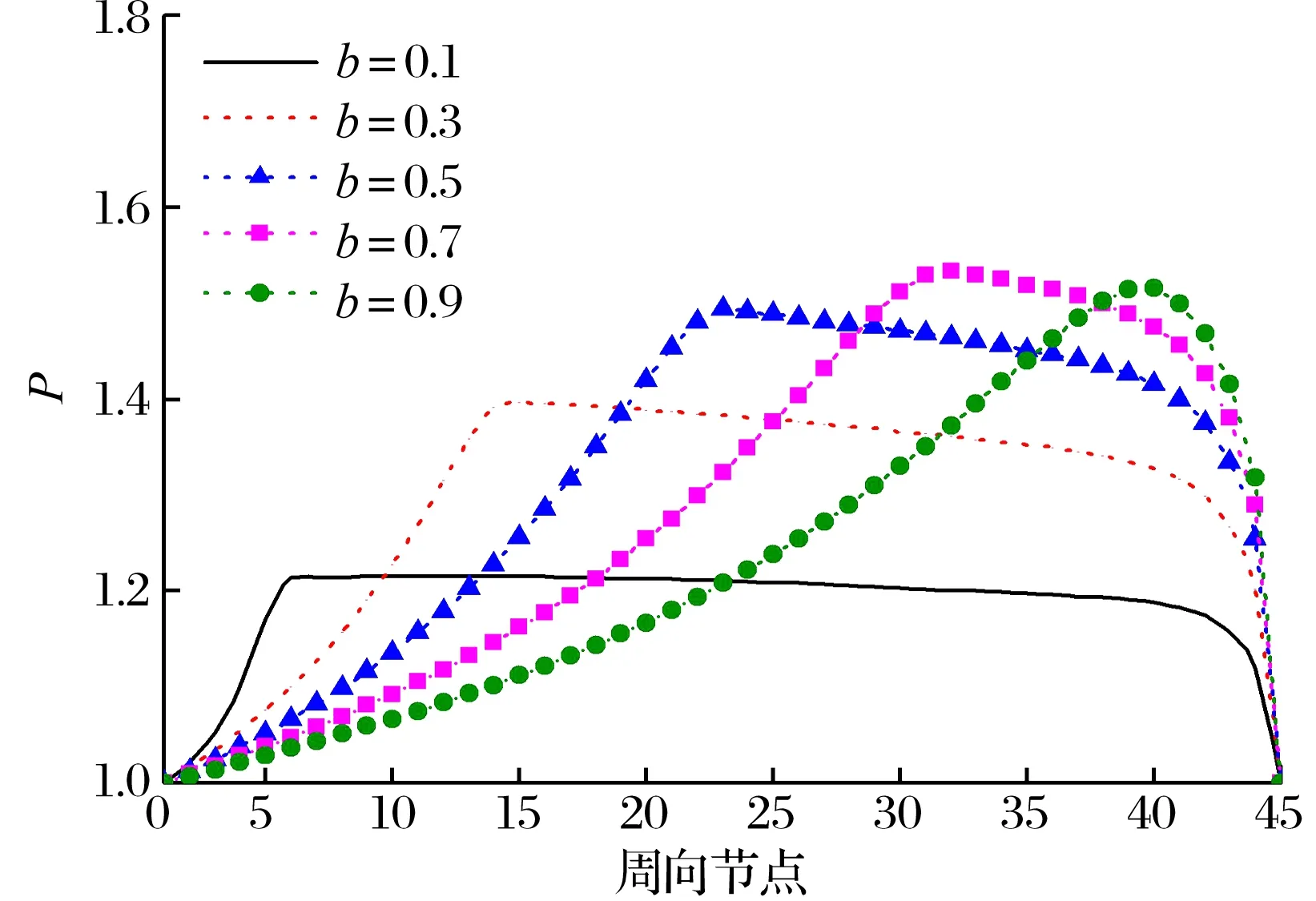
图9 不同节距比时周向量纲一的压力
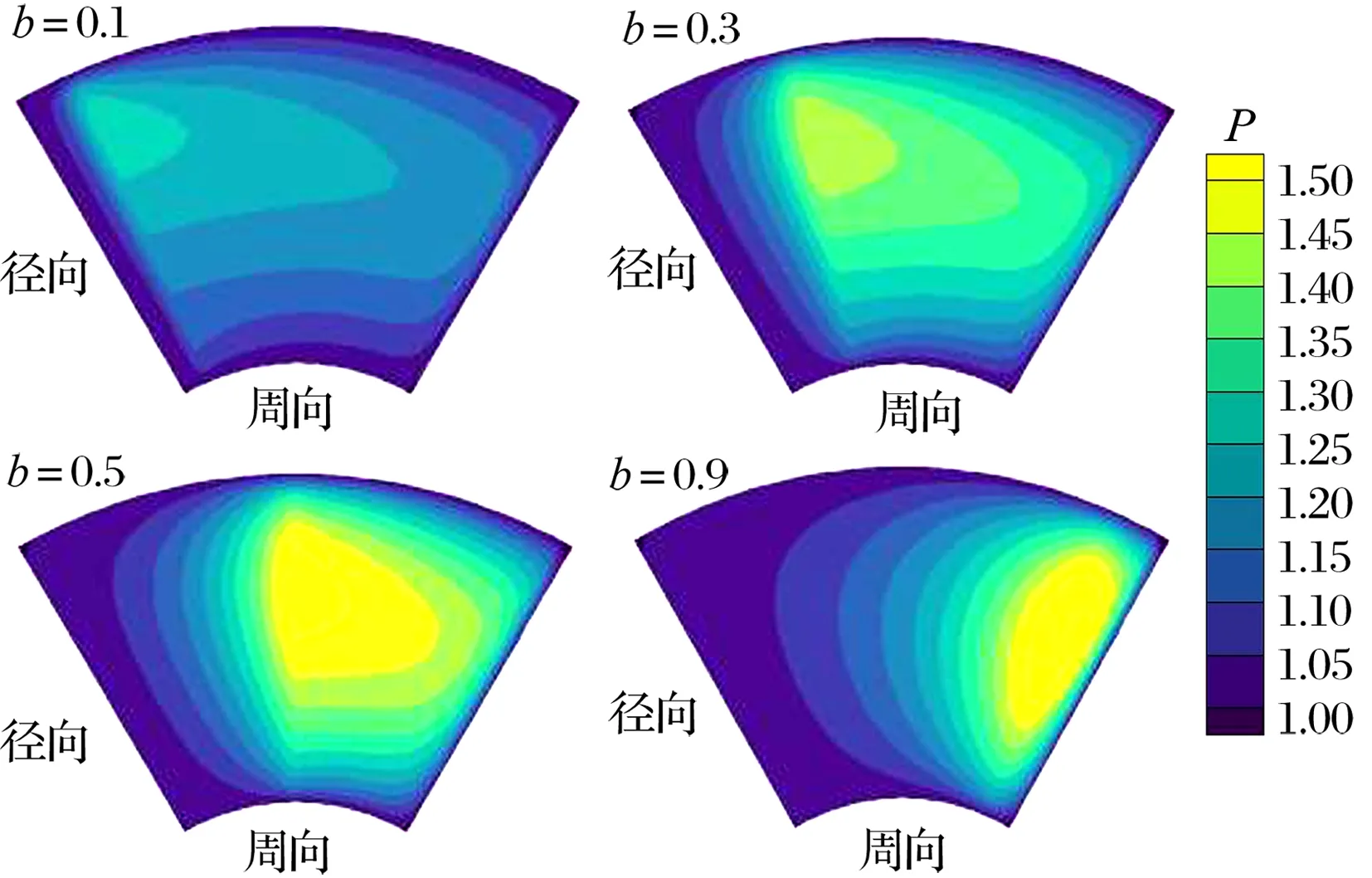
图10 不同节距比时量纲一的压力云图
2.2 楔形高度的影响
基于表2的计算参数,改变轴承楔形高度,得到轴承承载力及摩擦力矩随轴承楔形高度的变化关系,扇形瓦块中线沿周向的压力分布,不同楔形高度轴承量纲一的压力云图,结果如图11—图13所示:随着楔形高度的增加,轴承承载力呈先急剧增加后缓慢减小的趋势;摩擦力矩呈先急剧减小后缓慢减小的趋势;楔形高度为20 μm左右时,压力较高区域的面积占比较大,轴承承载力较大且摩擦力矩相对较小;楔形高度过小或过大时,轴承表面没有形成较大的高压区。

图11 承载力和摩擦力矩随楔形高度的变化
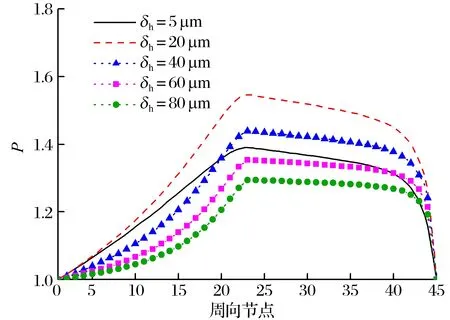
图12 不同楔形高度时周向量纲一的压力
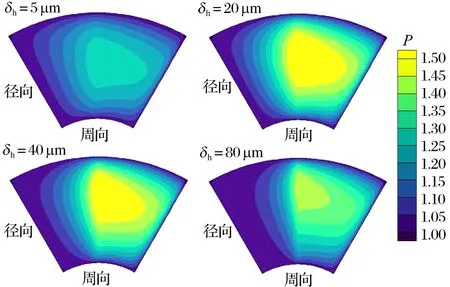
图13 不同楔形高度轴承量纲一的压力云图
2.3 瓦块数的影响
基于表2的计算参数,改变轴承扇形瓦块数,得到轴承承载力及摩擦力矩随瓦块数的变化关系,扇形瓦块中线沿周向的压力分布,不同瓦块数轴承量纲一的压力云图,结果如图14—图16所示:瓦块数较少时,轴承承载力没有太大变化;瓦块数超过6以后,扇形瓦块高压区域的面积占比减小,承载力明显减小,摩擦力矩持续增大;随着瓦块数的增加,周向上非楔形区域的压力分布更加平缓;瓦块数为6时,承载力较大且压力分布均匀,可认为此时轴承的性能最优。

图14 承载力和摩擦力矩随扇形瓦块数的变化
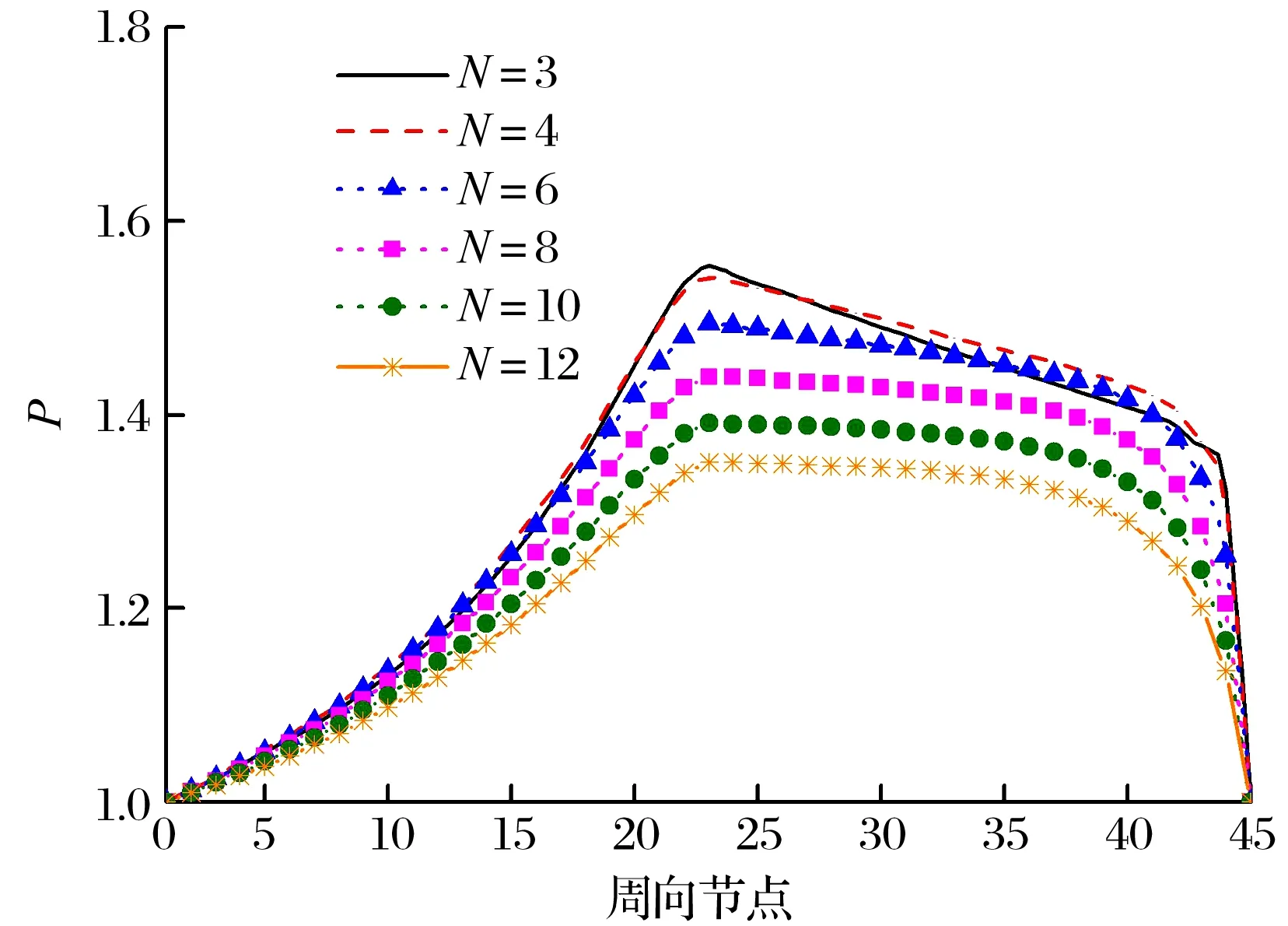
图15 不同扇形瓦块数时周向量纲一的压力

图16 不同瓦块数轴承量纲一的压力云图
3 结论
1)建立了波纹型止推箔片轴承的物理模型和求解轴承性能的雷诺方程、气膜厚度方程、箔片变形方程,与以往文献的对比验证了所编写求解程序的合理性,计算结果表明轴承承载力随箔片刚度的减小不断降低,随转速的提高不断增大。
2)选用内径12 mm、外径30 mm的止推箔片轴承进行数值仿真分析,结果表明轴承承载力和摩擦力矩随气膜厚度的增大明显降低。
3)轴承的结构参数对性能影响较大,其中节距比和楔形高度对轴承承载力的影响较大,当节距比为0.5,楔形高度为20 μm,扇形瓦块数为6时,轴承所表现出来的静态特性较优。
综上,在止推箔片轴承加工过程中,应尽量将节距比、楔形高度、瓦块数等结构参数控制在最优范围。
