解耦机构研究现状与分析

2022-10-21屈淑维郭志宏

机械传动 2022年10期

关键词：支链轴线并联

屈淑维郭志宏

（1 中北大学机械工程学院，山西太原 030051）

（2 恶劣环境下智能装备技术山西省重点实验室，山西太原 030051）

0 引言

当今自然界生物体所呈现的联结方式主要有串联、并联及混联。工程学中，人类所缔造的各类机械秉承了自然界万物的联结关系，这些联结关系通过铰链和构件形成了开环或闭环结构；为实现不同的功能需求，又形成了各类串联、并联及混联机构。

串联机构结构无耦合、控制容易，精度较低，被广泛应用在工程机械领域。并联机构结构紧凑、刚度大、承载能力强、累计误差小、精度高、工作空间小，被广泛应用于各类精密加工设备中。混联机构结构庞大、构型复杂，单模块化功能强，多被应用于大型及巨型装备的在线加工操作。

由于并联、混联机构存在闭环结构，机构控制困难、标定复杂、响应速度慢。而解耦机构可简化控制与标定，奇异位形少、工作空间大、运行精度高、能耗低，引起了学术界及产业界的广泛关注，成为机构学的研究热点之一[1]。

本文中通过研究解耦机构型综合方法及流程，揭示了解耦机构设计的关键技术是通过不同的驱动器实现独立的位姿输出；提出了支链解耦运动副轴线方向与位置的约束关系；根据支链输出运动特征，分析了驱动副选择原则；以输出运动解耦为目标，探讨了几类运动特征转化的设计方案；结合解耦机构的应用领域，指出了解耦机构的理论研究方向及应用拓展领域。

1 型综合方法

机构的型综合是根据输出运动特征进行设计，得到满足要求机构的过程。解耦机构是以机构运动与约束的变换逻辑关系为基础，以输出运动解耦为目标，通过输入/输出间独立的拓扑结构进行机构构型创新设计的过程。目前主要有4种理论方法。

1.1 线性变换

机构关节空间到输出运动空间及支链运动空间到机构输出运动空间的映射关系可表示为

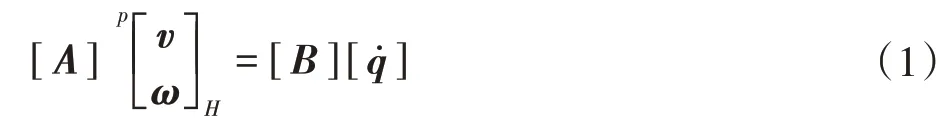
式中，[v]=[vx vy vz]为动平台输出点H的平移速度矢量；[ω]=[ωx ωy ωz]为点H的转动速度矢量；[A]为机构正向雅可比矩阵；[B]为逆向雅可比矩阵；q为笛卡尔坐标系中驱动副的输入速度。

式（1）可由线性变换表示为

式中，[J]=[A]-1[B]为全局雅可比矩阵，表示机构输入/输出的变换关系。

全局雅可比矩阵J（J-1）从理论上揭示了机构速度空间的映射关系，反映了机构的输入/输出特性。当雅可比矩阵为单位矩阵时，机构为各向同性机构；当雅可比矩阵为对角矩阵时，机构为不耦合机构；当雅可比矩阵为三角矩阵时，机构为解耦机构；否则为一般耦合机构。

Gogu[2]根据雅可比矩阵对各向同性机构、不耦合机构及解耦机构进行了型综合。基于线性变化理论，Glasunov 等[3-4]根据机构的雅可比矩阵进行了机构优选。雅可比矩阵从机构输入/输出映射上揭示了机构的运动特征。

1.2 基于单开链的约束综合法

并联机构是由动、静平台及两者之间的若干单开链（混合单开链）支路组成。单开链被视为机构的一种结构单元。机构的拓扑结构方位特征（POC）可表示为

式中，Mpa为并联机构的运动特征；MJi（i=1，2，…，m）表示支链的运动特征。

式（3）表明，机构的运动特征是所有支链运动特征的交集。

机构的拓扑结构特征由耦合度k表示为

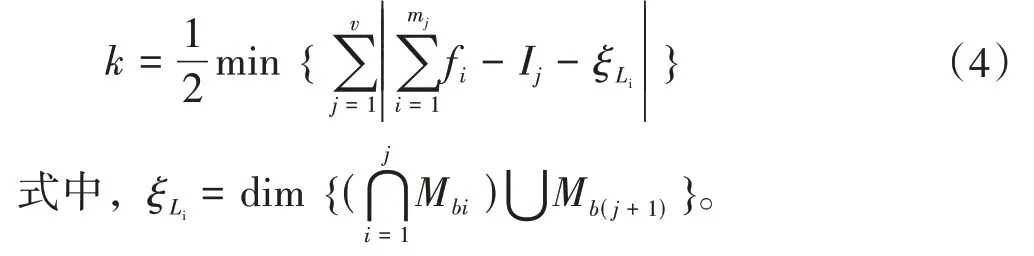
耦合度k揭示了多回路机构运动学与动力学的复杂性，为并联机构的解耦设计提供了理论依据。沈惠平等[5-6]以此为据进行了并联机构的位置解耦研究。Jin等[7]依据该方法融合拓扑结构及尺度参数对3自由度并联机构进行了解耦设计。

1.3 旋量理论

旋量由表达方向和位置的双矢量构成。通过机构的运动旋量系与约束旋量系，支链的运动旋量系与约束旋量系的互易（图1）与从属（图2）关系描述了机构的综合过程。

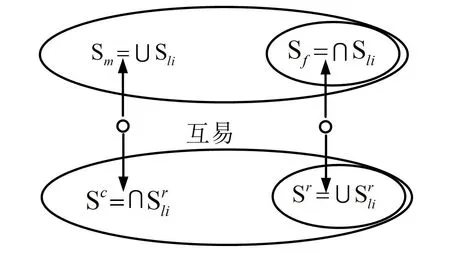
图1 机构旋量间的互易关系Fig.1 Reciprocal relation between mechanism screw

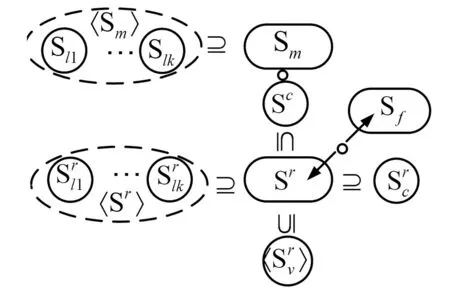
图2 机构旋量间的从属关系Fig.2 Affiliation between mechanism screw

将以上互易与从属关系用集合描述为机构运动旋量与支链运动旋量及机构约束旋量与支链约束旋量间的关联关系，建立机构输出与支链输出特征参数间的相互关系。以机构输出特征参数为目标依次确定支链的运动副配置，其型综合过程表示为

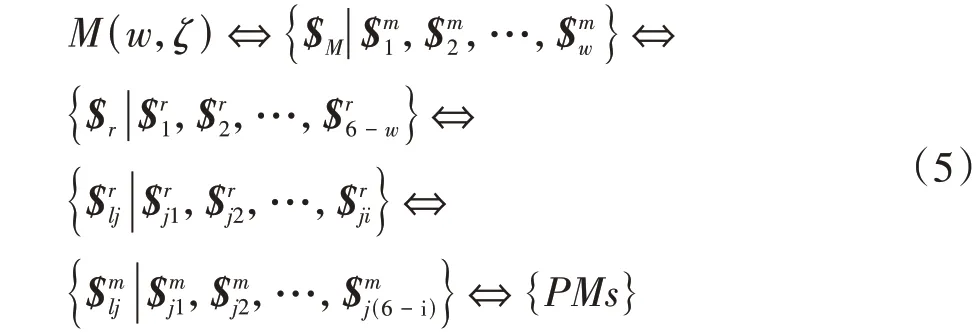
式中，w、ζ分别为机构输出自由度的数量和特征；$M、分别为机构及支链的运动旋量系；$r、分别为机构及支链的约束旋量系。

Qu 等[8]4根据旋量理论进行了并联解耦机构的型综合。张彦斌等[9]根据互易旋量理论，以分支的驱动旋量、主动旋量和可动非主动旋量间的相互关系，得到了3自由度各向同性平面并联机构。

1.4 GF集理论

GF集是机构末端速度特征的一种集合，依据转动特征与移动特征的拓扑关系，以Plücker 坐标为基础，描述拓扑结构关系。GF集的型综合过程可由式（6）～式（7）表示为

式中，GF为末端速度特征，GFi表示第i(i=1，2，…，n)条支链的末端速度特征。

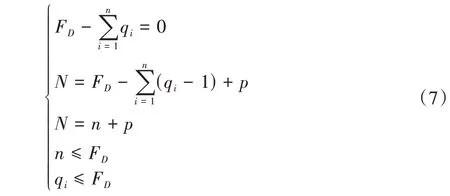
式中，FD为机构末端输出特征；N为支链数；n为具有主动驱动的支链数；qi为主动支链i上的驱动器数；p为被动支链数。

GF集的型综合主要依据移动特征与转动特征间的影响规律进行拓扑结构综合。影响规律表现为：①第一类六维全集GF集与任何其他GF集求交时不改变其他GF集的特征。②移动全集与任何其他GF集求交时不改变其他GF集的移动特征。③转动全集第二类GF与任何其他第二类GF集求交时，如果两个第二类GF集转动中心重合，则该转动全集GF不改变其他集GF的转动特征。

GF集依据机构移动特征与转动特征的相互影响及顺序性，准确描述了机构末端的运动能力。童幸等[10]基于GF集对3-DOF 解耦（可约）平移机构进行了型综合。秦友蕾等[11]根据铰链轴线的迁移规律，对3R2T并联机构进行了解耦综合。

上述几种型综合方法各有特色，为解耦机构的型综合提供了不同的解决途径。对上述几种方法特点的总结如表1所示。

表1 解耦机构型综合方法的分析Tab.1 Analysis of type synthesis method of decoupled mechanism

类型特点旋量理论GF集理论借助运动旋量系与约束旋量系间的对偶关系及旋量与反旋量间的互易关系。描述型综合过程。理论描述。依据运动副轴线间的方向与位置约束关系，揭示支链的输出运动规律，探索支链间的解耦关系。

上述几种方法从不同角度为解耦机构的型综合提供了理论依据。

2 解耦机构的型综合方法

解耦机构的本质是末端的输出运动特征能够通过不同的驱动器控制。当动平台的部分方位变量只是部分运动输入变量（θ1，θ2，…，θr）（r＜F）的函数时，机构的输入/输出变量间存在一一对应关系，机构完全解耦，表示为

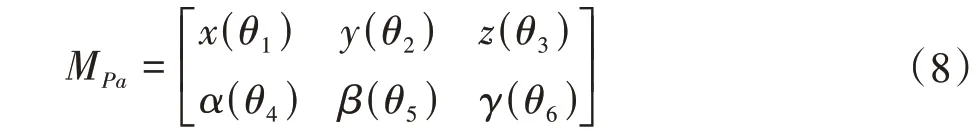
表示三角化结构为

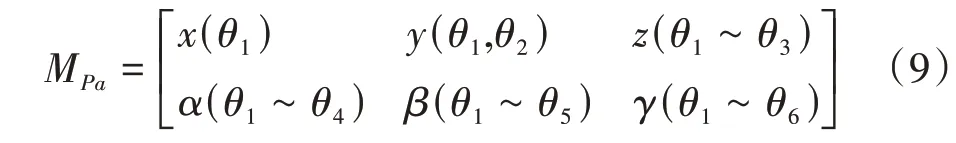
解耦机构的型综合方法为：根据解耦机构的输出特征，确定支链特征及运动副轴线的方向及位置的约束关系；验证机构的自由度；输出特性分析；若满足解耦输出特征，则综合机构为解耦机构，否则重新进行支链结构解方位特征配置。具体流程如图3所示。

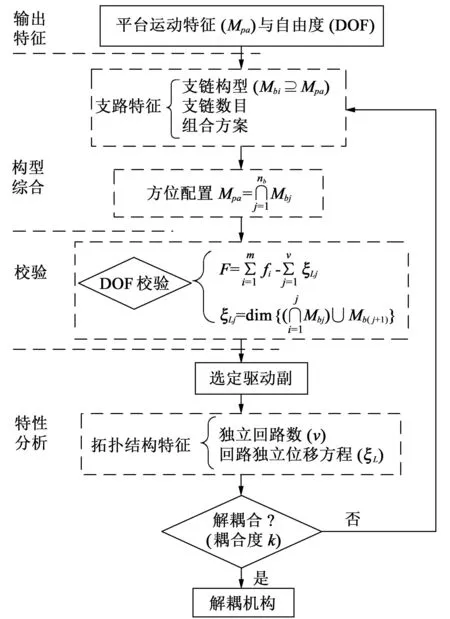
图3 解耦机构的综合流程Fig.3 Type synthesis procedure of decoupling mechanism

图3 表明解耦机构设计主要取决于3 个关键因素：①机构运动输出特征与各支链末端运动输出特征的关联关系（具有可分离自由度）。②支链的尺度参数（运动副轴线的几何及位置约束关系）。③驱动副的选择。

2.1 机构与支链输出特征关联关系

根据并联结构关系，机构部分从动件相对于机架的位置和方向只是部分驱动输入的函数时，该机构具有部分自由度，表示为

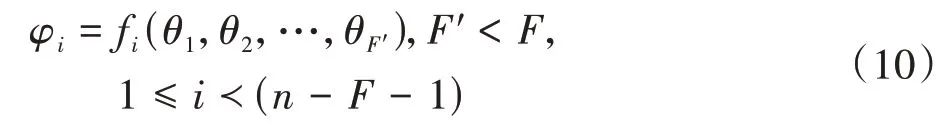
运动链拓扑结构关系可表示为

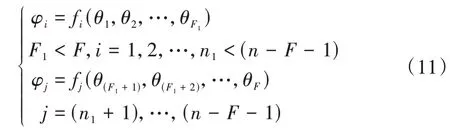
图4所示为自由度可分离的机构。该机构通过机架分离为两个独立运动链（SKC），且驱动副位于不同的SKC中，实现驱动与输出的一一对应。

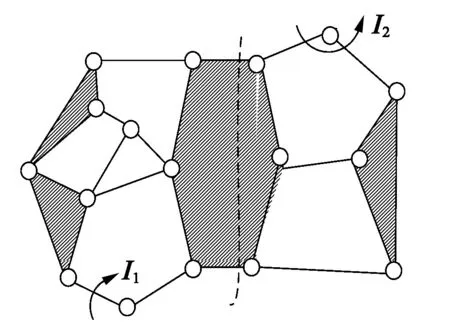
图4 自由度可分离机构Fig.4 Separable degree of freedom mechanism

2.2 支链解耦设计

支链解耦设计主要取决于运动副轴线间的约束关系。因此，在满足驱动副运动特征与支链中其他方向运动解耦的条件下，支链设计应满足以下条件：

（1）沿主动副轴线方向上，支路末端构件的输出必须为该支路主动输入的函数。

（2）若末端运动特征含有两个以上移动特征，则支链中的转动副轴线必须正相交或平行；移动副的轴线必须相互垂直。

（3）若动平台有转动输出要求，则所有支路的最后一个运动副应为转动副，且轴线必须与动平台转动输出轴线的方向一致。

2.3 驱动副的选择

为了提高机构运行过程中的稳定性，通常所有驱动副位于同一个平台。对预选的F个运动副为驱动副，将其刚化，得到新机构。需满足条件为

由于驱动副输入运动特征往往受轴线迁移的影响，因此，驱动副的选择应遵循以下原则[8]4：

（1）根据支链末端输出参数的特征要求，依次确定支链中运动副类型，且1个支链中最多只能含有1个转动输入特征。

（2）若支链的主动输入仅含有1个移动特征，则驱动副可为移动副、转动副或圆柱副；若输入运动为转动特征，则驱动副只能为转动副。

（3）若支链主动输入运动含有两个移动特征，第1个移动特征的驱动副只能选择移动副。

3 运动特征的转化方法

3.1 移动副转化

沿某一方向的移动副可用与该方向正交的转动副实现该方向的移动特征，可以改善机构的运动学与动力学性能，易于实现解耦控制。

图5 所示平行四边形4R 机构被定义为Pa 运动副。其相对运动存在两个特点：①构件A与构件B不存在相对转动。②增加了垂直方向的相对移动。在保持运动输出不变条件下，用四边形机构替代P副，能有效改善并联机构的性能。文献[12]借助该运动副特性进行了解耦机构的型综合。

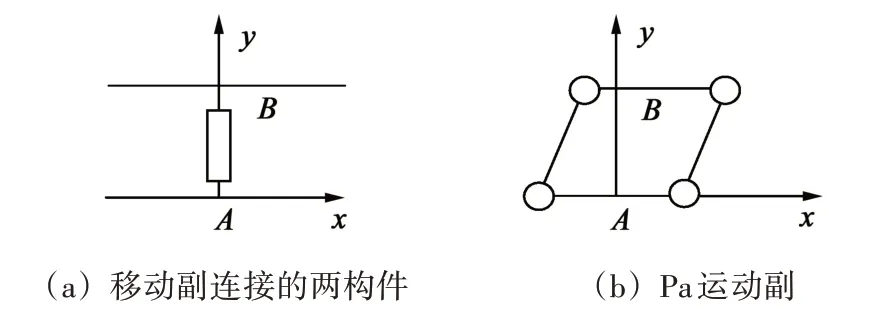
图5 移动副转化Fig.5 Prismatic pair transformation

类似特征的平行四边形机构具有输出构件相对于机架的姿态保持不变的运动特征，可有效消除机构的转动自由度，基本类型有4R、4U、4S平行四边形机构。

3.2 衍生运动设计

衍生运动亦称伴随运动。一般情况下，转动副往往衍生出垂直于其轴线方向的两个平移运动。如果输出有平移运动特征要求，则可用转动副作为驱动副，其衍生运动可实现其他两个正交方向上移动的输出解耦。

对于有几个独立转动方向输出特征要求的机构，衍生运动的消除是设计的难点。在设计中对于仅由转动副R 组成的单开链，每一构件的杆长与轴长皆为0，即所有转动副轴线交于一点（简称恒共点），该结构不存在衍生运动[13-14]，可实现只存在转动要求的解耦设计，如图6所示。

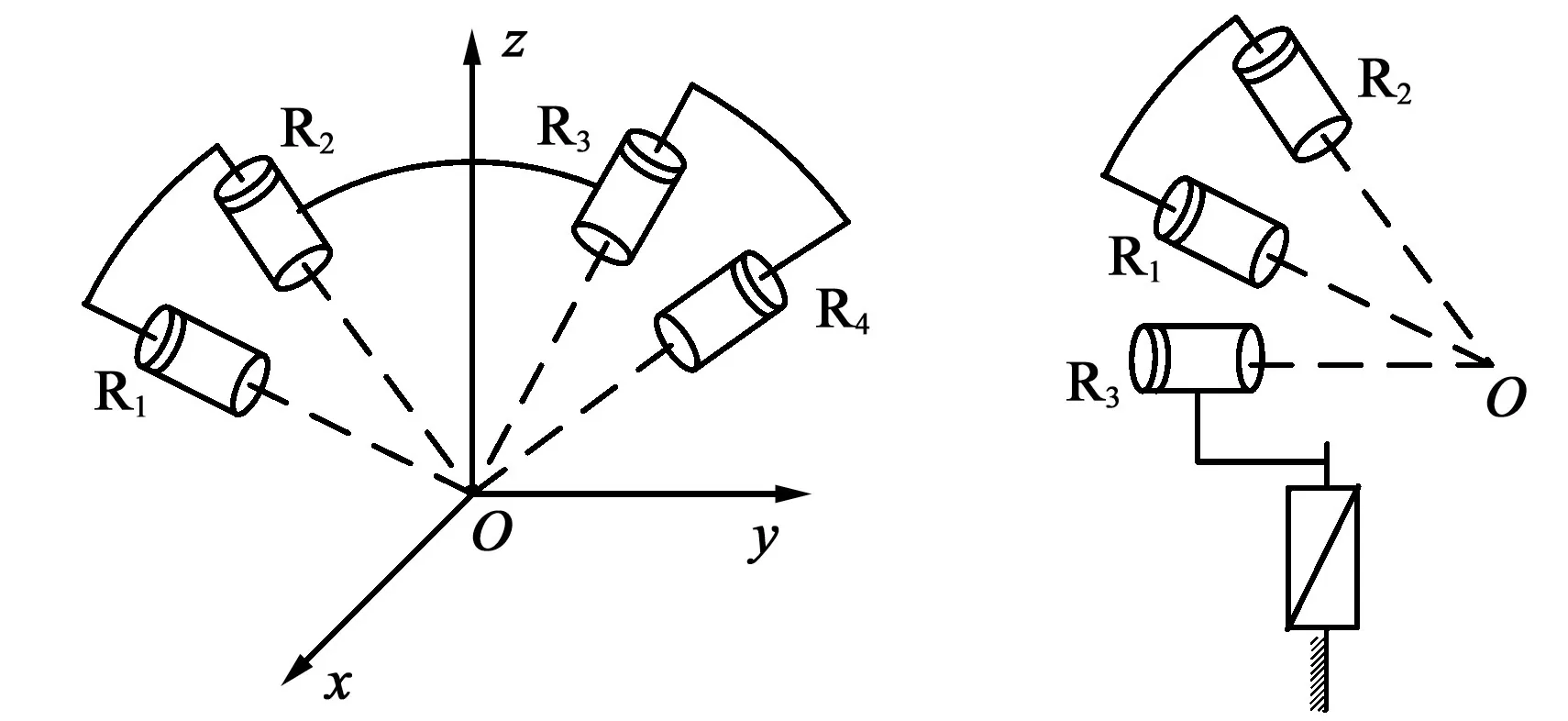
图6 转动副的恒共点设计Fig.6 Constant common design of rotating pair

Jin 等[15]以此为据，对解耦机构的结构约束特征进行了研究。张帆等[16]借助该结构设计了球面并联解耦机构。Li等[17]借助该结构对[P]S 类并联机构进行了无伴随运动的结构设计。

因此，当支链含有两维或三维共点转动特征时，转动中心的位置在移动特征的影响下会发生偏移。如图7（a）所示，当转动特征位于支链末端，支链末端的转动中心随支链中任一移动特征的变化而变化。此时，机构将丧失全部或部分转动能力。相反，图7（b）所示转动特征不受支链中移动特征的影响。因此，当运动链末端存在两维或三维共点转动特征需求时，应按转动特征在前、移动特征在后的顺序布置。

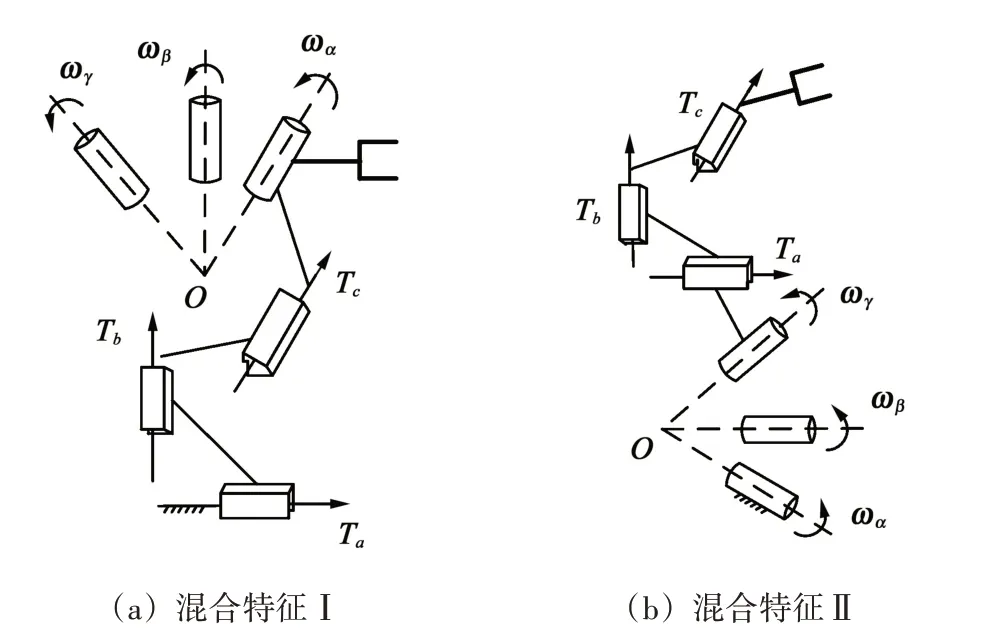
图7 混合特征单开联链解耦设计Fig.7 Hybrid characteristic single-open-chain decoupling design

4 解耦机构的应用现状

随着机构解耦技术的不断发展，在工业、航天、医疗和微机械等诸多领域得到了广泛应用。本节从应用的角度鸟瞰解耦机构的应用研究进展，希望能有更多的学者及工业界人士关注研究解耦机构，进一步拓宽其应用的领域与空间。

4.1 解耦机构与工业

平面解耦操作手可在大工作空间实现位姿的灵活变换，被用于大幅面光电产品的检测及大型工件的加工操作（加工、焊接、喷涂）[18]。基于连续转轴的2 自由度转动机构可用于天线定向、摄像机跟踪、太阳能定位等2自由度转动领域[19]。3自由度多轴并联解耦数控机床样机为装备制造业提供了有力的技术支撑[20]。混联机床运动学的解耦设计，大大提高了控制精度，使工业产品的合格率得到了大幅提高。全解耦3平移多维振动筛可获得多个工况下物料颗粒的筛分，输入、输出具有完全解耦的并联筛分机构，使茶叶在筛面上快速均布，有效避免茶叶堵塞筛孔，从而提高筛分效率；其振动幅度、频率和振动自由度都能独立调节且便于控制，可实现不同品种茶叶的筛分[21]。

4.2 解耦机构与航天工程

航空航天领域中的微器件（微卫星、微陀螺、微加速度计、微传感器）具有结构尺寸小、精度高等特点。振动性能、可靠性、高灵敏度性能测试是这类微器件测试领域的难题。2 自由度及3 自由度柔性解耦并联机构，可实现平台的微定位及精确定位，能够满足微器件的测试需求。多维柔性解耦并联机构则可被应用于加速传感器的测试实验[22]。

二维微定位自解耦装置[23]实现了光刻物镜检测平台的准确定位。全柔性微动全解耦并联激振台具有相同的振动规律与振动频率，容易控制。2自由度转动解耦的角度调整装置[24]可用于改变高密度封装中芯片姿态。弹性整体运动副[25]并联解耦六维力传感器无运动副的安装间隙和偏载、结构简单、稳定性好、易于制造和安装。星球探测车通过采用补偿铰链解耦法可满足其在崎岖地形平稳运行的能力。

4.3 解耦与医疗

近年来，面向生物工程、医学工程的微操作解耦机器人受到国内外学术界和工程界的广泛关注，发展速度极快，已被应用于实现细胞的注射分割及微外科手术等。3T2R 并联解耦机构被用于外科手术的头部支架[26]。2T2R 机构[27]被用于外科的注射系统。6 自由度解耦并联机构[28]被用于长骨骨折的回复机构。远程全解耦并联机器人被用于外科手术[29]。两个解耦并联机构混联机器人[30]可用于腹腔镜手术，实现了微创手术操作的技能要求。Kuo 等[31]研发的解耦并联机构被用于腹腔手术的空间定位机构。

5 发展趋势

解耦机构的型综合过程与数学之间存在着不同层次的联系，数学方法如图论、集合论、矢量代数、旋量理论、李群、多项式理论、迭代法、同伦法等可直接应用于机构学。

随着机构解耦技术的发展与成熟，解耦机构已延伸到军事、生产、生活、康复医疗等诸多领域。解耦设计方法由单一的技术设计向多学科的交叉与融合发展；解耦结构由刚性向刚柔一体化结构发展；应用空间由工农业领域向航天、航空及精密领域延拓。

并联解耦机构在学术及应用领域引起了极大关注，尤其在解耦措施上，涌现出了多种方法。但目前尚未从理论高度形成系统化的解决方案。解耦机构各种性能指标的定量描述与分析为解耦机构设计及应用提供有效的技术支撑，有利于助推解耦机构向高科技领域延伸。在工农业及日常生活服务领域，将具有解耦特性的并联机构承载于机器人系统，也将产生巨大的应用空间。