基于观测器的混沌电力系统PI固定时间自适应滑模控制

徐敏，康哲，刘早富

基于观测器的混沌电力系统PI固定时间自适应滑模控制

徐敏，康哲，刘早富

(南昌大学信息工程学院，江西 南昌 330000)

为对九阶电力系统中的混沌现象进行控制，基于有限时间观测器将PI控制与固定时间终端滑模控制相结合，提出一种控制电力系统混沌的新方法。有限时间观测器可对外来干扰进行预估，积分的加入可消除系统稳态误差。同时对传统滑模的固定切换控制项通过加入自适应律从而进行改进，进一步加强控制方法鲁棒性。利用tanh(/)函数代替传统滑模的符号函数以及利用新的趋近律来解决滑模控制中的抖振现象。最后为缩减控制参数寻找时间，在构建一种新的目标函数基础上利用改进蚁狮算法对控制参数进行寻优。结果表明所提出的控制方法具有良好的控制性能。

混沌控制；有限时间观测器；固定时间滑模；PI控制；蚁狮算法

0 引言

非线性系统有时会产生复杂的现象即混沌现象，混沌现象在自然界以及人类社会中广泛存在[1]。电力系统作为一种典型的非线性系统，在发生参数变化、时滞或外来扰动时，系统可能会出现如低频振荡、同步谐波振荡等现象[2-3]，甚至会导致混沌的现象的产生，此时会引起系统过电压、过电流，严重时会发生互联电网断裂现象[4]。随着“碳中和”、“碳达峰”目标的提出，新能源正大量加入电力系统中，电力系统的运行环境变得更加复杂[5]，可能会使电网局部发生的混沌状况演变为电力系统整体性混沌，从而使整个系统崩溃[6-10]。由此，电力系统混沌现象的控制对电力系统的保护有特殊的意义。

目前众多学者对电力系统混沌现象控制进行了大量的研究，但多数学者研究的系统模型都是在文献[11]七阶电力系统上简化得到的二阶、四阶模型，如献[12-13]分别利用非奇异滑模和全局滑模对二阶电力系统进行控制；文献[14]为提高控制系统的收敛速度以及抗干扰能力，将时滞控制与全局滑模相结合对四阶电力系统进行混沌控制；文献[15]在全局滑模的基础上为加快控制的收敛性使用快速全局滑模对四阶电力系统进行混沌抑制；文献[16]利用非奇异滑模控制对四阶电力系统混沌进行控制，虽然上述研究均取得了较好的效果，但其研究模型较为简单，难以扩展到高阶系统模型中，也有部分学者针对七阶电力系统混沌进行抑制[17]，少有学者对次暂态电势的九阶系统模型进行混沌控制研究，该模型是目前研究混沌控制模型中最为复杂，且能反映实际电力系统的基本运行规律，对该模型的抑制对保证整个电力系统稳定运行具有重要的现实意义。

滑模控制具有的对模型参数和干扰不灵敏等优点使得其在控制领域应用较广[18-20]，但其存在抖振现象。为改善滑模控制的缺点，许多学者在经典滑模控制的基础上提出了各种方法，文献[21]利用自适应理论从干扰的角度对抖振现象进行削弱，但其对抖振现象削弱较小；文献[22]使用饱和函数来代替传统滑模的符号函数，以此来减弱抖振现象，但此方法需在控制性能和抖振两个方面进行抉择；文献[23]利用继电器特性函数代替符号函数削弱抖振现象，但其没有保留符号函数中良好的性能，文献[24]将滑模控制输出进行模糊化处理从而减弱抖振现象，但其未对滑模面本身进行改进。

控制方法的鲁棒性对工程实际具有特别重要的意义，在处理干扰的各种方法中，基于观测器的控制方法由于对系统模型的依赖性低而具有重要的实际价值[25]，自适应理论对干扰也具有一定的削弱作用。对于控制器参数的确定，大多采用试错法进行寻找[26]，但越复杂的系统其控制器参数会变得越多，从而使控制器参数的寻找变得更加繁琐，优化算法的加入可以很好解决这个问题。文献[27-29]使用蚁狮算法对控制器参数进行寻优，但蚁狮算法初始化影响算法性能，需对其进行改进。

综上所述，本文在九阶电力系统的基础上，对电力系统存在的混沌现象提出一种PI固定时间终端滑模控制，将PI与固定时间滑模相结合可以对系统误差进行消除；对于抖振现象，利用tanh(/)代替传统滑模的符号函数以及利用新的趋近律来减弱抖振现象；对于外来干扰的影响，利用一种有限时间观测器对干扰进行预估，从而消除其对控制性能的影响，为进一步增强控制方法鲁棒性，在传统滑模控制的切换控制项中加入自适应律；为了得到较优的控制参数，利用改进的蚁狮算法在构建新的目标函数上对控制参数进行优化以得到较好的控制性能。

1 电力系统模型及混沌分析

1.1 系统模型描述

本文采用考虑次暂态电势在内的九阶电力系统模型[30]，根据系统各参量的耦合情况，将系统分为3个子系统，含控制输入的数学模型如式(1)所示。

在受控系统表达式的各个变量中，gIIt为各状态变量的函数，变量之间的具体耦合关系见文献[31]，系统其他变量均为常值参数，如表1所示。

图1为电磁功率m= 1.361时的系统状态图，由图1可知，此时系统各状态量均处于不规则振荡中，为展现系统从正常状态到混沌状态的动态过程，以电磁功率m为分岔系数，将参数范围设为[1.2,1.5]，则可得到系统状态变量分岔图。

表1 仿真模型的参数

图1 系统各状态时序图

图2 系统分岔图

图3 系统功谱图

图4 Pm=1.361时的系统相图

由图3可以看出，当m= 1.361时，功率谱是连续谱信号且含有高直流分量和低频分量，并且功率谱出现宽带噪声，这是典型的混沌特征。

图4为m= 1.361时的系统相图，由相图可知，系统在经过一段时间后变为混沌振荡状态，系统相图中存在奇怪的吸引子，这是系统混沌状态的特征之一。

以上现象表明，当m= 1.361时，系统中出现了混沌现象，混沌状态的出现不利于系统的稳定运行，必须抑制混沌振荡的发生。

2 有限时间观测器的设计

电力系统运行时会出现外部因素干扰以及参数扰动带来的内部干扰，为减弱各种扰动给系统带来的影响，以增强系统的鲁棒性，在系统控制时加入观测器以对干扰进行预估，一种有限时间观测器可设计为[32]

通过式(2)对干扰进行预估，则可在有限时间内得到扰动的估计值。

引理1[33]存在以下系统：

证明：定义以下误差。

对式(4)进行求导并代入式(3)可得

结合式(3)和式(4)，则式(5)可变为

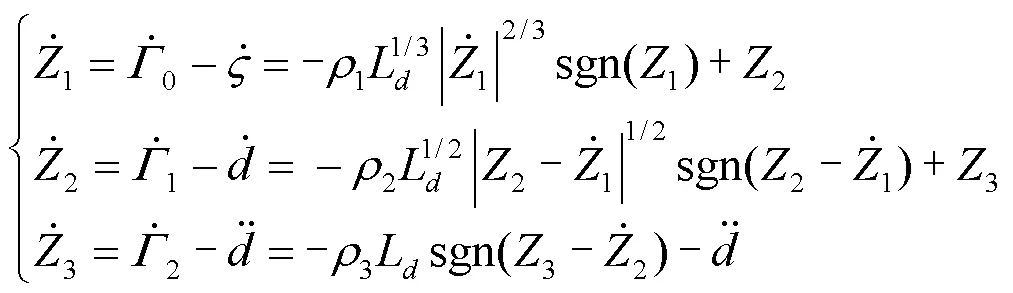
证明完毕。

3 电力系统混沌控制器设计

3.1 滑模面的构造与比较

考虑到固定时间滑模面具有较快的收敛速度，能够在有限时间内达到稳定，在固定时间滑模的基础上与PI控制相结合得到新的滑模面，如式(7)所示。

符号函数虽可以使系统的状态快速趋近滑模面，但会带来抖振，为进一步改善控制效果的抖振现象，选用tanh(/)代替符号函数，不仅可以保持符号函数的优点，还能减弱符号函数本身的抖振性，最终构建的滑模面为

为了比较滑模面收敛的快慢，以经典倒立摆系统为对象，将式(9)所构滑模面与文献[15]和文献[34]所构建的滑模面进行比较，将文献[15]作为对比滑模面2，将文献[34]作为对比滑模面1，结果如图5所示。

从图5可以看出，在收敛速度方面，式(9)所构建的滑模面有明显的优势。

3.2 控制器的设计

对于式(1)所示的系统，通过各个变量的耦合情况设计3个控制输入对整个系统进行控制，则可将系统分为3个子系统，各子系统表达式为

子系统一：

子系统二：

子系统三：

对于滑模控制的趋近律，基于固定时间理论，对传统的固定时间方程式进行改进，新构造的趋近律表达式为

对于滑模控制的切换控制项，利用自适应的滑模切换项对传统的切换控制项进行改进，从而可以优化滑模控制的性能，其表达式为

结合式(14)—式(18)可得最后控制律为

构造李雅普诺夫函数：

对式(23)进行求导，可得

将式(19)—式(21)代入式(24)中，可得

4 蚁狮优化算法

蚁狮算法于2015年提出，是一种随机搜索算法，它模仿了自然界中蚁狮的狩猎行为。根据蚁狮的捕猎方式为蚁狮建立陷阱，然后蚁狮在陷阱中诱捕蚂蚁，蚂蚁以随机游走方式寻找食物，蚂蚁陷入陷阱并被捕捉，蚁狮重建陷阱等待下次捕食。

在蚁狮算法中蚂蚁种群类似于粒子群算法中的粒子群，每一次蚂蚁被蚁狮捕捉即完成一次迭代。蚂蚁在自然界中寻找食物时是随机移动的，因此，蚂蚁在优化过程中每一步的随机行走定义为

蚂蚁种群在优化的每一步都以随机行走的方式更新它们的位置。但由于每个搜索空间都有一个边界，故需要对式(27)进行归一化处理。

当存在蚁狮陷阱时会对蚂蚁的随机行走产生影响，其数学建模可以表述为

当蚁狮意识到陷阱里有一只蚂蚁，它们就会将沙子扔向洞穴边缘。这种行为会使试图逃跑的被困蚂蚁滑下去。为了对这一行为进行数学建模，需自适应地减小了蚂蚁随机游动的大小，其数学建模可以表述为

式中，为比例系数，其表达式为

式中：为当前迭代次数；为最大迭代次数。

捕猎的最后一个阶段是蚂蚁到达坑底，被蚁狮吃掉，然后，蚁狮需要更新自己的位置，跟上被猎杀蚂蚁的最新位置，以增加捕捉新猎物的机会。数学建模可以表述为

为保证迭代后蚂蚁种群的全局多样性，通过以下方式来进行蚂蚁种群的迭代。

传统的蚁狮算法中用随机函数进行初始化，为提高初始种群的随机性，使种群均匀地分布在优化区域内，采用改进的初始化方法，即将初始化分为若干区域，在各子区域内采用Logistic映射模型来初始化种群，这样可使种群在参数范围内更加随机分布。

对于优化的目标函数，本文以控制要求的“稳”“准”“快”为起点，对于准的指标，选取积分时间绝对误差为性能标准，对于稳和快的性能指标，选取超调量、上升时间、过渡时间和峰值时间为性能指标，所提出的目标函数如式(35)所示。

通过本文的控制器设计，得到基于蚁狮优化的电力系统PI固定时间自适应滑模控制策略的控制框图，如图6所示。

图6 基于蚁狮优化的PI固定时间自适应滑模控制框图

5 仿真结果

图7 控制后系统各变量状态图

图8 控制后系统相图

将本文所用方法与文献[15, 34]所用方法进行对比，将文献[34]的方法作为对比方法1，文献[15]所示的方法作为对比方法2，结果如下。

从图9(a)和图9(b)可以看出，在抖振方面，本文所提改进型方法与方法2均较好，但在对比方法1中，抖振问题仍然存在，其幅值均大于1×10-4；从图9(c)和图9(d)可以看出，在收敛速度方面，改进型方法的收敛速度比其他两个方法均优越；在稳态误差方面，改进型方法也较小，而两个对比方法的稳态误差均大于1×10-4。

图9 状态对比图

图10 不同趋近律状态变量对比图

从图10可以看出，在抖振方面，传统的固定时间趋近律存在较为明显的抖振现象，其抖振的幅值为2.5×10-4；并且在收敛速度上，改进的趋近律也较为快速；在超调量上，改进的趋近律明显的减小。

图11为在周期性干扰下自适应切换律和传统固定值切换律对比图，以状态变量δ为对比量，在周期性干扰下，自适应切换律相比传统切换律具有更好的控制性能，在收敛速度和超调量上，自适应切换律控制效果都比传统切换律更优。

图11 干扰下状态变量对比图

图12 有无观测器的对比图

图13为有限时间观测器的输出值，从图13可以看出，观测器能在1 s内实现对干扰的实时预估，这表明观测器的有效性。

图13 观测器输出值

6 结论

1) 本文对较为复杂的九阶电力系统模型进行混沌振荡控制，对九阶系统模型进行简化可得到七阶、六阶、四阶和二阶模型，但九阶电力系统控制的成功可以说明，不必再对其他低阶电力系统模型进行控制研究，本文控制方法可为实际解决电力系统混沌振荡现象提供一定思路。

2) 提出了一种基于观测器的电力系统PI固定时间终端滑模控制，将九阶电力系统分为三个子系统，将固定时间滑模控制理论与PI控制相结合得到新的滑模控制方法，从而对系统中的混沌现象进行抑制。对于滑模控制中的抖振现象，利用tanh(/)代替传统滑模的符号函数，以及利用新的趋近律来对其进行抑制。

3) 针对外来周期性干扰和系统参数扰动等集中干扰，本文利用自适应律和有限时间观测器对干扰进行处理，以增强系统稳定性，在干扰下控制器能够使系统在有限时间收敛到期望值，并可以快速消除系统中存在的混沌振荡现象，通过对比说明了所用方法具有较好的鲁棒性。

4) 考虑控制系统参数调节复杂以及费时费力的情况，利用优化的蚁狮算法对控制方法进行参数寻优，根据控制性能的要求构造出新的控制目标函数，从而使控制效果朝更好控制性能优化。

[1] 雷绍兰, 孙才新, 周湶, 等. 基于改进加权一阶局域预测模型的短期负荷预测方法研究[J]. 电测与仪表, 2006, 43(5): 5-8.

LEI Shaolan, SUN Caixin, ZHUO Quan, et al. The research on short-term load forecasting method based on improving adding-weight one-rank load forecasting model[J]. Electrical Measurement & Instrumentation, 2006, 43(5): 5-8.

[2] 宋墩文, 杨学涛, 丁巧林, 等. 大规模互联电网低频振荡分析与控制方法综述[J]. 电网技术, 2011, 35(10): 22-28.

SONG Dunwen, YANG Xuetao, DING Qiaolin, et al.A survey on analysis on low frequency oscillation in large-scale interconnected power grid and its control measures[J].Power System Technology,2011, 35(10): 22-28.

[3] 方洁, 许丹莹, 方娜, 等. 四阶电力系统混沌分析与新型滑模控制[J]. 华中师范大学学报(自然科学版), 2020, 54(3): 391-397, 404.

FANG Jie, XU Danying, FANG Na, et al. Chaotic analysis and new sliding mode control for fourth-order power system[J]. Journal of Central China Normal University (Natural Sciences), 2020, 54(3):391-397, 404.

[4] DEEPAK K L, SWARUP K S. Modeling and simulation of chaotic phenomena in electrical power systems[J]. Applied Soft Computing, 2011, 11(1): 103-110.

[5] 孙伟卿, 罗静, 张婕. 高比例风电接入的电力系统储能容量配置及影响因素分析[J]. 电力系统保护与控制, 2021, 49(15): 9-18.

SUN Weiqing, LUO Jing, ZHANG Jie. Energy storage capacity allocation and influence factor analysis of a power system with a high proportion of wind power[J]. Power System Protection and Control, 2021, 49(15): 9-18.

[6] 刘劲, 孙扬声, 陈德树. 周期参数扰动电力系统中的倍周期分叉、混沌和奇怪吸引子[J]. 电网技术, 1996, 20(8): 1-3, 8.

LIU Jin, SUN Yangsheng, CHEN Deshu. Period doubling, chaos and strange attractors in power system disturbed by periodic parameter[J]. Power System Technology,1996, 20(8): 1-3, 8.

[7] 贾宏杰, 余贻鑫, 李鹏. 电力系统环面分岔与混沌现象[J]. 中国电机工程学报, 2002, 22(8): 6-10.

JIA Hongjie, YU Yixin, LU Peng. Torus bifurcation and chaos in power system[J]. Proceedings of the CSEE,2002, 22(8): 6-10.

[8] 葛润东, 刘文颖, 郭鹏, 等. 电力系统低频振荡预警及动态阻尼控制策略研究[J]. 电工电能新技术, 2015, 34(2): 7-12.

GE Rundong, LIU Wenying, GUO Peng, et al.Research of low-frequency oscillation warning and dynamic damping control strategy in power system[J].Advanced Technology of Electrical Engineering and Energy,2015, 34(2): 7-12.

[9] 马鹏飞, 李华, 于梦洋, 等. 高斯白噪声扰动下的电力系统混沌振荡抑制[J]. 计算机测量与控制, 2014, 22(2): 578-580, 583.

MA Pengfei, LI Hua, YU Mengyang, et al. Control of chaos in power system under Gaussian white noise[J]. Computer Measurement & Control, 2014, 22(2): 578-580, 583.

[10] 徐明. 拟周期扰动下一类电力系统的混沌行为[J]. 江汉大学学报(自然科学版), 2011, 39(1): 30-32.

XU Ming. Chaos of a power system under quasi-period disturbance[J]. Jianghan University (Natural Science Edition), 2011, 39(1): 30-32.

[11] RAJESH K G, PADIYAR K R. Bifurcation analysis of a three node power system with detailed models[J]. International Journal of Electrical Power & Energy Systems, 1999, 21(5): 375-393.

[12] 胡茗, 杨晓辉, 王毅. 基于鲁棒反演滑模法的电力系统混沌控制[J]. 电测与仪表, 2019, 56(3): 129-132, 138.

HU Ming, YANG Xiaohui, WANG Yi. Chaos control in power system based on robust back-stepping sliding method[J]. Electrical Measurement & Instrumentation, 2019, 56(3): 129-132, 138.

[13] 于永进, 王家斌, 王艳. 基于自适应全局滑模的电力系统混沌振荡控制[J]. 电力系统保护与控制, 2019, 47(16): 43-49.

YU Yongjin, WANG Jiabin, WANG Yan.Chaotic oscillation control in power system based on adaptive total sliding mode[J].Power System Protection and Control,2019, 47(16): 43-49.

[14] 杨洋, 于永进, 王云飞. 基于全局滑模时滞的电力系统混沌振荡控制[J]. 电力系统保护与控制, 2021, 49(15): 59-67.

YANG Yang, YU Yongjin, WANG Yunfei.Power system chaotic oscillation control based on global sliding mode time delay[J]. Power System Protection and Control,2021, 49(15): 59-67.

[15] 李小腾, 王江彬, 刘崇新, 等. 四阶混沌电力系统的全局快速滑模控制器设计[J]. 科学技术与工程, 2021, 21(24): 10298-10303.

LI Xiaoteng, WANG Jiangbin, LIU Chongxin, et al. Global fast sliding mode controller design for a four-dimensional chaotic power system[J]. Science Technology and Engineering, 2021, 21(24): 10298-10303.

[16] 王家斌, 于永进, 阎振坤, 等. 基于自适应非奇异终端滑模控制的电力系统混沌抑制[J]. 电力系统保护与制, 2021, 49(7): 120-126.

WANG Jiabin, YU Yongjin, YAN Zhenkun, et al.Chaotic suppression of a power system based on adaptive non-singular terminal sliding mode control[J]. Power System Protection and Control, 2021, 49(7): 120-126.

[17] 王江彬, 刘凌, 刘崇新. 七阶电力系统混沌振荡的动态面滑模控制[J]. 电机与控制学报, 2021, 25(4): 1-8.

WANG Jiangbin, LIU Ling, LIU Chongxin. Dynamic surface sliding mode control of chaotic oscillation in a seven-dimensional power system[J]. Electric Machines and Control, 2021, 25(4): 1-8.

[18] ASL R M, HAGH Y S, ANAVATTI S, et al. Adaptive finite integral non-singular terminal synergetic control of nth-order nonlinear systems[J]. Mechanical Systems and Signal Processing, 2020, 142: 1-10.

[19] KUMAR A, ANWAR M N, KUMAR S. Sliding mode controller design for frequency regulation in an interconnected power system[J]. Protection and Control of Modern Power Systems, 2021, 6(1): 77-88.

[20] 黄宵宁, 倪双飞, 杨成顺, 等. 带指令滤波的直驱永磁风机自适应反推积分滑模控制[J]. 电力系统保护与控制, 2020, 48(22): 142-150.

HUANG Xiaoning, NI Shuangfei, YANG Chengshun, et al.Adaptive backstepping integral sliding mode control of a direct-drive permanent magnet wind generator with a command-filter[J]. Power System Protection and Control, 2020, 48(22): 142-150.

[21] HUANG Wendi, MIN Fuhong, WANG Zhulin, et al. Chaotic oscillation suppression of the interconnected power system based on the adaptive back-stepping sliding mode controller[C] // 2015 14th International Symposium on Distributed Computing and Applications for Business Engineering and Science,August 18-24, 2016,Guiyang, China: 463-467.

[22] WANG Jiabin, YU Yongjin. Chaotic oscillation control in power system based on adaptive linear feedback sliding mode control[C] // IEEE Chinese Automation Congress,November 23, 2019, Hangzhou, China: 3384-3388.

[23] HACHANA A, HARMAS M N. Terminal synergetic control for blood glucose regulation in diabetes patients[J]. Journal of Dynamic Systems Measurement and Control, 2018, 140(10).

[24] 倪骏康, 刘崇新, 庞霞. 电力系统混沌振荡的等效快速终端模糊滑模控制[J]. 物理学报, 2013, 62(19): 107-113.

NI Junkang, LIU Chongxin, PANG Xia.Fuzzy fast terminal sliding mode controller using an equivalent control for chaotic oscillation in power system[J].Acta Physica Sinica, 2013, 62(19): 107-113.

[25] LI Shihua, YANG Jun, CHEN Wenhua, et al. Generalized extended state observer based control for systems with mismatched uncertainties[J]. IEEE Transactions on Industrial Electronics, 2012, 59(12): 4792-4802.

[26] ELSISI M. Optimal design of nonlinear model predictive controller based on new modified multitracker optimization algorithm[J]. International Journal of Intelligent Systems,2020, 35(11): 1857-1878.

[27] BONDALAPATI S, CHANDEL A K. Ant-lion optimizer algorithm based fractional order proportional-integral- derivative controllers for islanded operation of an inverter based microgrid[C] // 2021 IEEE Kansas Power and Energy Conference,April 19-20, 2021, Manhattan, KS, USA: 1-6.

[28] PRADHAN R, MAJHI S K, PRADHAN J K, et al. Optimal fractional order PID controller design using ant lion optimizer[J]. Ain Shams Engineering Journal, 2020, 11(2): 281-291.

[29] RAJU M, SINHA N. Automatic generation control of a multi-area system using ant lion optimizer algorithm based PID plus second order derivative controller[J]. International Journal of Electrical Power and Energy Systems, 2016, 80(9): 52-63.

[30] VAHDATI P M, KAZEMI A. Bifurcations and chaos in nonlinear dynamics of power systems[C] // IEEE 2016 24th Iranian Conference on Electrical Engineering, May 10-12, 2016, New York, USA: 1706-1711.

[31] WANG Jiangbin, LIU Ling, LIU Chongxin, et al. Fixed- time synergetic control for a seven-dimensional chaotic power system model[J]. International Journal of Bifurcation and Chaos, 2019, 29(10): 1-8.

[32] OMAR M, XU Limei, HUANG Ya, et al. Observer-based fixed-time continuous nonsingular terminal sliding mode control of quadrotor aircraft under uncertainties and disturbances for robust trajectory tracking: theory and experiment[J]. Control Engineering Practice, 2021, 111.

[33] SHTESSELA Y, SHKOLNIKOVB I, LEVANT A. Smooth second-order sliding modes missile guidance application[J]. Automatica, 2007, 43(8): 1470-1476.

[34] SONG Junhong, SONG Shenmin, ZHOU Huibo. Adaptive nonsingular fast terminal sliding mode guidance law with impact angle constraints[J]. International Journal of Control, Automation and Systems, 2016, 14(1): 99-114.

Observer-based PI fixed time adaptive sliding mode control for chaotic power systems

XU Min, KANG Zhe, LIU Zaofu

(School of Information Engineering, Nanchang University, Nanchang 330000, China)

To control a chaotic phenomenon in the ninth-order power system, a new method for controlling the chaos of the power system is proposed. This combines PI control and fixed-time terminal sliding mode control based on a finite-time observer. The finite-time observer can predict the external disturbance, and the addition of the integral can eliminate the steady-state error of the system. The fixed switching control term of the traditional sliding mode is improved by adding an adaptive law to further enhance the robustness of the control method. The tanh(/) function is used to replace the sign function of the traditional sliding mode and a new convergence law is used to solve the chattering phenomenon in the sliding mode control. Finally, in order to reduce the control parameter search time, a new objective function is constructed based on an improved ant-lion algorithm to find the optimal control parameters. The results show that the proposed control method has good control performance.

chaos control; finite time observer; fixed time sliding mode; PI control; ant-lion algorithm

10.19783/j.cnki.pspc.211651

国家自然科学基金项目资助(51967013)

This work is supported by the National Natural Science Foundation of China (No. 51967013).

2021-12-04；

2022-04-02

徐 敏(1963—)，女，博士，教授，研究方向为电力系统分析及控制；E-mail: xumin-8660@163.com

康 哲(1998—)，男，通信作者，硕士研究生，研究方向为电力系统运行与控制。E-mail:17721048331@163.com

(编辑 许 威)