基于知识图谱和模糊推理的机械故障诊断模型

石玉，胡瑛婷

（山东师范大学 信息科学与工程学院，山东 济南 250358）

0 引 言

随着第四轮经济全球化、第四次工业革命的到来，物联网、人工智能技术在制造业得到普遍应用，全球制造业格局正发生战略性调整。人工智能等技术促使“智能工厂”“智能车间”“智能工作流程”等的诞生，极大地降低生产制造成本。智能制造是中国制造从“大”走向“强”的重要方向，是中国顺应科技革命和产业变革的总趋势，建设创新型国家的战略性选择。

目前，制约生产的一个重要因素是设备维护，现有的主要维护方式分为：修复方式，预防方式和预测方式。随着工业大数据的发展和人工智能与工业大数据的结合，预测性维护成为相关研究的重要应用场景。预测性维护可以避免故障停机或最小化故障停机时间，保证机器能在尽可能长的时间内正常使用，研究价值高。祝旭倡导将过去常用的预防性维护转变成基于设备状态是否正常的预测性维护，可见预测性维护对工业生产的重要意义。若对预测性维护的相关研究方法进行简要分类，可分为基于机器学习和基于本体方法。

机器学习算法是人工智能技术的核心之一，能够处理高维度数据、多变量数据等复杂数据，并且可以获取复杂环境与动态环境中数据之间的隐藏关系，在预测性维护技术中应用前景广阔，相关研究成果也较为丰富。目前应用于故障诊断和预测性维护的机器学习算法主要有：逻辑回归、支持向量机、决策和随机森林等算法，以及近年来发展最快的深度学习算法：人工神经网络算法和深度神经网络算法。深度神经网络算法是一种具备多隐藏层的神经网络，当每层单元数和层数明显增多时，能更好的代表经典人工神经网络的复杂函数。但机器学习方法也有局限性，如存在数据问题、复杂与个性问题、不确定性问题、黑箱问题、AI 芯片问题等待解决。

基于规则的相关研究首先需要构建一个知识库，知识库以关于域的语句形式存储计算模型符号，并通过操作符号来执行推理。通常，本体被认为是“对感兴趣的领域进行概念性的规范”，是抽象知识。OntoProg是一个为方便预测性维护定义的一个通用本体，具有严格概念化的国际标准，主要用于预测机械部件的剩余使用寿命。MPMO是一种制造预测维护本体，对领域本体进行了进一步扩展。刘鑫采用七步法构建本体，建立本体类owl 文件，通过SPARQL 查询、SWRL 推理，为知识共享通用型智能化故障诊断技术提供一种思路。规则形如“If-Then”的推理，如模糊推理能对领域专家的解决问题过程进行编码，且已经被用于智能产品设计，在故障分类中也有模糊相关应用。

然而，现阶段大部分的设备维护系统的策略知识可复用性低，信息共享程度低，设备维护智能化程度也较低。基于此，本文试图提出一种基于知识图谱的，可解释性强的故障诊断方法。参考机器学习算法将数据映射为高维向量，本文将知识图谱映射到模糊本体，同时对数据赋予语义信息并做进一步封装，通过模糊推理得到故障程度。而模糊推理能将“模糊性”概念具体化，满足实际工业生产环境的需求。

1 机械故障诊断模型

本文使用基于规则的方式构建预测性维护模型，首先构建机械故障知识图谱，为设备故障赋予多方面语义信息；然后定义模糊本体，并确定模糊概念等关键内容；将知识图谱映射到模糊本体，使用第三方工具包实现自动推理，得到故障模糊值。并兼顾横向与纵向分析，得出本文模型的有效性。

在实验阶段，本文以一个真实的液压系统数据集为例进行研究，纵向得到四个评价指标，横向与支持向量机（Support Vector Machine，SVM）进行对比。基于本文构建的图谱、本体，可实现对相关工业集群的故障诊断，进一步完善可实现预测性维护任务。本文模型构建及验证流程如图1所示。

图1 模型构建及验证流程

知识图谱能挖掘各知识间的规律，具有较高的参考价值。本文借助机械领域权威学者发布的论文及其他相关研究成果，构建上层本体，同时结合数据集的特性自下而上完成构建。继现代控制理论后，又出现了智能控制理论。模糊控制是智能控制的组成部分。模糊推理是从不够精确的给定前提集合中推理得到可能的不够精确的结论解的过程，已被证实，大部分数模糊系统是万能函数逼近器，能完成任意的非线性连续控制规律和动态模型。将构建完成的机械知识图谱，映射到定义的模糊本体，可在模糊推理前为每条数据赋予语义信息。

1.1 构建设备故障知识图谱

知识图谱由语义网络演变而成，通过构建机械故障知识图谱，能全面深入地表达知识的层级结构与语义关系。目前知识图谱的构建方式主要有两种：自顶向下（top-down）与自底向上（bottom-up）。自顶向下的方法是先从顶端的概念开始定义，然后逐步精确；自底向上与之相反，先定义实体，然后归纳总结形成底层的概念，逐步向上抽象形成上层的概念。

本文通过“自上而下”“自下而上”相结合的方式构建机械故障知识图谱。自上而下能确保构建的领域本体具有通用性，自下而上能确保构建的本体具有实用性。根据机械领域权威学者发布的论文《Basic Concepts and Taxonomy of Dependable and Secure Computing》，及其他相关权威机构发布的本体，自顶向下初步完成构建机械故障知识图谱。

结合多种数据集的共性，实现自底向上补充、完善构建的机械故障知识图谱。最终得到的知识图谱是自顶向下构建的图谱的子图谱，且对其中的组件具体化，如图2所示。

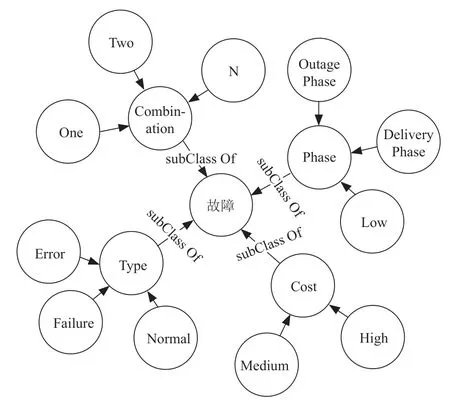
图2 机械故障知识图谱

通过自上而下、自下而上的方式，完成了机械故障知识图谱的构建。该知识图谱既高度综合概括了领域专家的知识，也能应用于实际的传感器数据集。构建的知识图谱能为获取的时序数据集赋予语义信息，可用于多方面分析机械设备故障发生的原因及影响。

1.2 构建模糊推理模型

根据上文构建的知识图谱，选取核心内容作为模糊本体构建的关键，可依据具体情况有针对性的修改模糊本体。本文的模糊本体模型主要由四部分组成：设备故障程度，故障发生阶段、故障设备维修费用和故障设备组合。构建完成的模糊本体如图3所示，其中，设备组合共有四种情况。

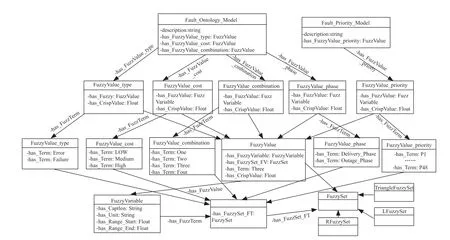
图3 模糊本体图

值得注意的是，模糊与概率都可以用来刻画不确定性，但概率是事件是否发生的不确定性，而模糊是事件发生的程度。本文提出的算法推理得到的结果，即为设备出现故障的故障程度，是模糊值而非概率。

1.2.1 定义模糊概念

模糊概念包括模糊变量（Fuzzy Variable）、模糊集（Fuzzy Set）及模糊值（Fuzzy Value）。模糊变量用来描述一个普遍性模糊概念。模糊变量由变量名、变量的单位、变量的数值域和一组能描述该变量的特定模糊概念的模糊术语组成。其中，模糊术语（FuzzyTerm）通过术语名称、对应的模糊集定义。

模糊集表示在模糊变量范围内的隶属度；模糊值编码模糊语言表达式。其中，隶属度函数的确定是影响模糊推理结果准确度的重要因素。隶属度函数是用精确的数学方法描述具有模糊性的概念，实质反映了事物渐变性。

由模糊本体可知，本模型定义的与输入有关的模糊变量包括：设备故障类型type，具有Error、Failure 两个模糊术语；故障发生阶段phase、具有Outage Phase、Delivery Phase、Shutdown Phase 三个模糊术语；故障设备维修费用cost，具有Low、Medium、High 三个模糊术语；故障设备组合Combination，模糊术语定义为某一时刻可能发生故障的设备数，包括：One、Two、Three、Four 四个术语。定义的与输出有关的模糊变量为priority，依据四个模糊变量，十二个模糊术语，共定义四十八条模糊规则，对应四十八个模糊变量priority 的模糊术语P1、P2、……P48.

1.2.2 定义模糊规则

模糊规则（Fuzzy Rule）的输入为模糊变量的定义区间的数值，通过模糊规则，可得到输出模糊变量的定义区间的值。一条模糊规则拥有三组模糊变量，分表代表规则的输入、前提和结论。规则通常写为：

If A1 and A2 … and A3

Then B1 and B2 … and B3

根据前提和规则数目不同，模糊推理时需要遵循的隶属度复合规则也不完全相同。具体可以分为：单一前提单一规则、多前提单一规则、多前提多规则。本文提出的模型算法使用多前提多规则。

2 实验：液压系统故障模型

2.1 数据集选择及预处理

实验部分选用UCI 机器学习仓库的液压系统数据集进行测试，用以验证所提模型的有效性和准确性。数据集中共有四种部件，每种部件有3 或4 个状态，如表1所示。数据集中的故障标签与部件给出的描述不符，故重新为数据集添加标签。原数据集共2 205 条数据，经清洗去重后剩144 条，将每条数据的每个部件按照故障程度（degree）求和并归一化，以0.7 为阈值添加标签，共得到33 条标签为故障的数据，占23%；111 条标签为正常的数据，占77%，较符合实际场景。

表1 四个部件的状态描述

2.2 液压系统故障知识图谱

结合第三节定义的机械故障知识图谱，将液压系统数据集输入为知识图谱的数据层，挖掘出数据集中更丰富的语义信息，从而构建液压系统故障子知识图谱。数据集中共有四种部件，每种部件有多个不同的状态，通过分析每个部件的故障程度type、维修费用cost、故障发生时所处阶段phase，定义每条数据的状态：

（1）故障程度类型（type）：故障程度分为Error 与Failure，其中Failure 的严重程度定义为高于Error。结合论文中提到的故障程度定义及数据集特点，作如下定义：若该条时序数据中含有Failure，则该时序数据故障程度类型定义为Failure；若仅有Error 而无Failure，则定义为Error。

（2）维修费用（cost）：维修费用划分为：Low、Medium、High.不同部件不同状态权重和维修费用定义如表2所示。此处维修费用权重的定义与部件价格、易损程度、维修难度等有关。

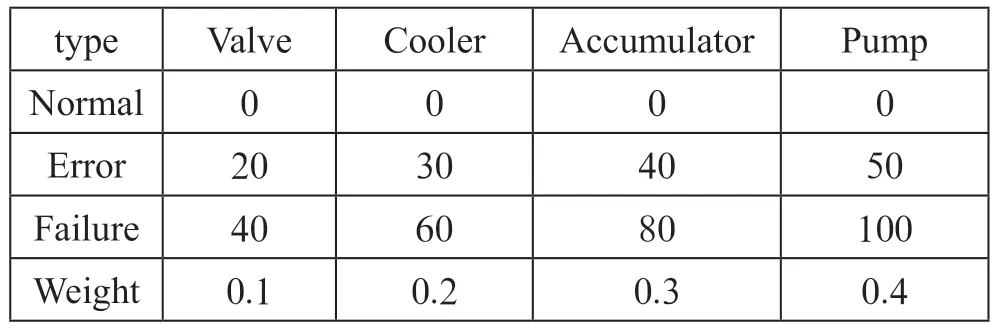
表2 四个部件维修费用定义

（3）故障发生时所处的阶段（phase）：分为outagephase、deliveryphase、shutdown phase.其中，所用数据集中没有处于shutdown phase，若存在故障程度为Failure的部件，则定义为outage phase；deliveryphase 定义为，出现故障的时序数据中非outage phase。

（4）发生故障的部件组合数（combination）：某一时刻液压系统发生故障的部件种类数有：1、2、3、4。

综上，数据集中每条数据均有四个特征，每个特征有多个特征值，如表3所示。

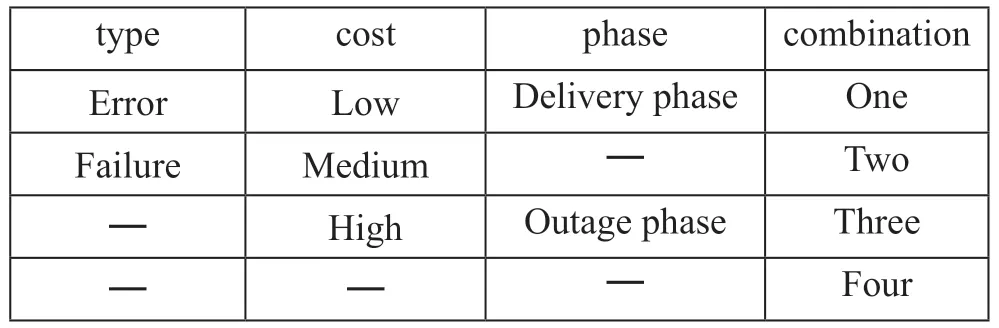
表3 四个特征及对应值

2.3 映射到模糊本体

四个特征等价于模糊本体的四个模糊术语，实现了知识图谱到模糊本体的映射。模糊本体的构建是模糊推理的前提，模糊推理的流程是：定义模糊术语及模糊变量、选择隶属度函数、定义推理规则、得到模糊值结果。

将四个特征以对应的模糊变量的模糊术语作为输入。隶属度函数分为Z 函数、S 函数、Ⅱ函数，本模型主要使用的是Ⅱ函数中线性函数、三角函数。此处的部分线性函数可简化为经典集合，用梯形函数拟合。维修费用的三个模糊术语高、中、低分别对应斜率为负的直线、三角函数、斜率为正的直线，区间分别为[0，30]，[0，30，60]，[30，60]，其中60 为计算得到的维修费用的最高值。类型、组合、阶段的模糊术语分别是垂直于水平轴的单值直线，实验部分使用梯形函数近似，梯形隶属度函数公式定义如公式（1）。

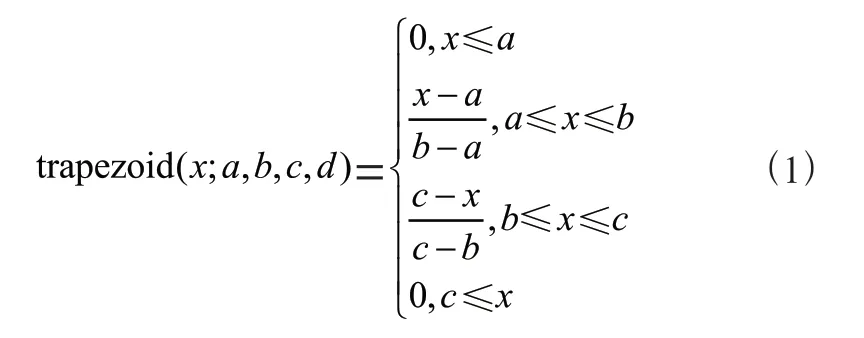
2.4 规则库构建

建立规则库是机械设备故障预测性维护方法的核心。将不同特征排列组合得到不同场景下的规则，并将这些规则录入到规则库中，通过FuzzyJ Toolkit 模糊推理机制获取该场景下的故障模糊值。

由表3可知，每条数据有四个状态、每个状态对应的2～ 4 个值，经排列组合可得48 种状态，依照表中，自左向右、自上而下故障严重程度依次递增的规则定义，构建模糊推理规则库。规则库是模糊推理的核心，由一至多条形如为“if - then”的语句组成。参数过多会导致推理规则繁杂，影响推理效率。本文定义了48 条规则，具体规则如下，其中优先等级priority 的值设定为1 最低，48 最高。规则示例如下：

If type is Error and cost is low and combination is one and phase is delivery_phase

then set priority to priority 1

…

If type is Failure and cost is high and combination is four and phase is outage_phase

then set priority to priority 48

48 条规则与模糊变量priority 的48 个模糊术语对应，作为模糊本体模型定义规则的输出结论定义。模糊变量priority 的隶属度函数使用三角函数。

3 结果及分析

3.1 本文模型结果分析

第三方工具包FuzzyJ Toolkit 提供了在Java 中建立模糊概念和推理的能力，通过定义模糊概念、模糊规则后，对144 条数据进行模糊推理并得到模糊值。设定阈值为数据添加推理标签，并与原标签进行对比可以验证模型的有效性。

准确率能反映预测标签与真实标签的一致率，但在某些场景下不能反映真实需求，因此引入了精确率、召回率和F1 值，对结果进行较为全面的分析。

精确率是指模型预测为正实际也为正的样本，占被预测为正的样本的比例。计算公式如（2）：

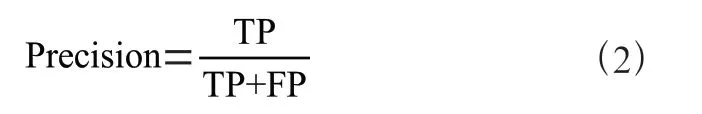
只用精确率来评价模型也是不完整的，引入召回率。召回率定义为：实际为正的样本中，预测值为正的样本占实际为正的样本的比例。计算公式如（3）：

F1 score 是精确率和召回率的调和平均值，计算公式如（4）：

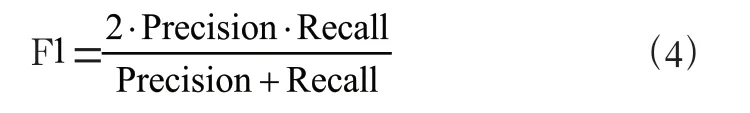
其中，FP 表示实际为负且预测为正的样本数，TN 表示实际为负且预测为负的样本数，TP 表示实际为正且预测为正的样本数，FN 表示实际为正且预测为负的样本的数。

分别以0.8、0.85、0.9、0.95 为阈值为数据添加推理的故障标签，并与数据集的原有标签进行比较，从准确率、精确率、召回率和F1 四个方面评价模型，结果如表4所示。当阈值设定为0.9 时，准确率最高，为0.84，其他阈值的准确率也都在0.5 以上。模型的精确率普遍较低，召回率普遍较高，当阈值为0.9 或0.95 时，F1 值达到0.67。可见，本文提出的模型效果较好；其中，当阈值为0.9 时，效果最佳。

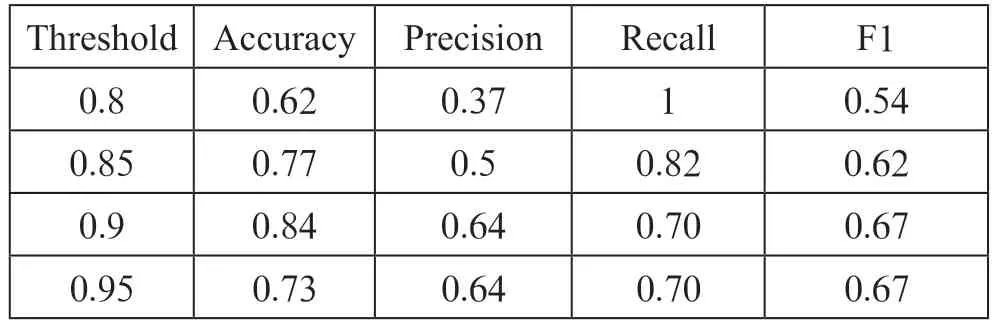
表4 模型训练结果四个特征及对应值

3.2 与SVM 结果对比分析

支持向量机（support vector machines，SVM）是一种经典的二分类模型，通过求解能够正确划分数据且几何间隔最大的超平面，分类数据。SVM 能够解决小样本下机器学习问题，且泛化能力较强。将最大间隔超平面的上下两个超平面定义为|ωx-|=1，其中与未知，SVM 的目标函数如公式（5），约束条件如公式（6）。

将数据集划分为训练集和测试集，采用交叉验证方式训练液压系统数据集的SVM 模型，得到更为可靠稳定的模型。交叉验证的K 值的选取对训练出的模型影响较大，故采用两个常用的K 值：5 和10 进行测试。scikit-learn 的SVM 模型中参数random_state 用于控制伪随机数的生成，如果不指定，每次结果差距较大；经测试，选用0 或1 时效果较好；其他参数使用scikit-learn 默认参数，使用SVM 训练结果如表5所示。

表5 SVM 训练结果

由表5可看出，当选取10，random_state 选取1 时，效果最好。在相同时，不同的random_state 表现出不同的效果；而random_state 相同时，=10 优于=5。

3.3 对比分析

由3.1 和3.2 可以看出，经典二分类算法SVM 在模型评估中表现出较大优势。四个指标中，论文提出的模型仅在召回率上略胜一筹。但这并不能否定本论文提出的模型的有效性。

从原理上看，实验部分使用的数据集的标签均是更新后的，仅以故障程度为依据为数据集添加标签，缺少其他影响因素的加权，不符合实际生产环境，也与本论文提出的模型存在原理上的区别。故障程度只是本文构建的机械故障知识图谱的一部分。

从模型特点来看，SVM 算法与本文提出的模型各有优势。SVM 算法的优势在于，充分挖掘数据中的信息，建立尽可能逼近源数据的模型，得到期望的结果。而SVM的缺点，也是其他机器学习算法的通病是：模型难以解释。当机器学习算法将多维数据映射到向量空间，建模后虽然能得到预期的结果，但原有的语义信息难以保留，也难以将模型结果向非专家进行解释，同时模型的随机性较强，不同的随机种子对结果影响较大。这也是本文模型提出的关键原因。

本模型基于语义信息建模，构建了机械故障知识图谱，映射到模糊本体进行模糊推理，整个过程数据具有唯一性。事实上，大部分数模糊系统是万能函数逼近器，通过调整模糊变量的模糊函数，也可以得到最大可能与源数据标签一致的结果，但对于本文使用的数据集，调参意义较低。

最后，虽然在四个指标上本文模型较差于SVM，但这四个指标只能在一定程度上反映模型效果，而不能决定模型的效果，本文提出的模型依旧是有效的，并且在合适的数据集上可能表现地与SVM 同样好。

4 结 论

本文针对预测性维护问题，提出了一种基于知识图谱和模糊推理的故障诊断模型（代码已开源：https：//github.com/satatata-ai/KG_AND_FR）。构建了机械故障领域知识图谱、构建模糊本体，并以映射的方式，沟通知识图谱和模糊本体，通过模糊推理得到故障模糊值，进而诊断设备状态。在预处理后的液压系统数据集上，表现效果较好，取阈值为0.9，准确率能达到0.84，F1 值为0.67。与经典二分类模型SVM 对比分析得出，本文模型是有效的。在合适的数据集上，本文模型能表现出与SVM 同样较好的效果，此时若模型落地实际工业生产，本文模型在可理解、可针对性修改模型参数方面更具有优势。

本文提出的模型具有通用性，不仅适应于液压系统，也可对其他工业集群进行故障诊断。工业生产过程中真实可靠的数据集难以获取，选择更合适的数据集进行模型检验也是接下来的任务之一。

本文模型实现了设备的故障诊断，但仅是故障诊断并不能做到预测性维护。进一步地，在本模型的基础上，添加时间序列预测模型，如ARIMA 模型，对历史数据推理出的故障模糊值进行预测，以指定时间范围出现故障次数为依据判断整个设备状态是否稳定并预警，可实现预测性维护任务目标。