基于线性矩阵求解的焊接缺陷几何量定征技术研究

周红明，张小杰

（1.丽水学院工学院，浙江 丽水 323000；2.浙江晨雕机械有限公司，浙江 丽水 323000）

超声TOFD成像检测技术对焊缝缺陷的定量不依赖于缺陷波的幅值，而与超声波达时间有关，相比其他的无损检测方法具有其独特的优势。因此，超声TOFD成像检测技术是焊缝缺陷无损定量检测的最佳手段之一[1-2]。在超声TOFD检测过程中，为了防止漏检，最有效的方式是增加超声波声束在被检工件中的扩散范围，就是使用具有大扩散角的超声换能器。但是大扩散角所带来的问题是在检测成像过程中会产生大量的冗余信息，其会干扰缺陷几何量的确定。比如对工件进行超声TOFD的D扫描成像检测时，由于冗余信息的存在，检测图像中会出现明显的双曲线特征，因此很难从检测图像中直接读取缺陷的几何量信息，这已成为了超声TOFD成像检测缺陷定量化精确测量技术发展的瓶颈因素[3-4]。

为解决上述问题，国内外的一些学者开展了一系列相关的研究，如哈尔滨工业大学刚铁等[5]利用SAFT技术将超声TOFD检测图像在线性化的基础上进行合成孔径聚焦处理，以此来提高检测图像的分辨率。Spies等[6]利用SAFT技术在一定程度上消除了冗余信息的影响，提高了检测图像的横向分辨率。Maalmi等[7]采用Hough变换将超声TOFD检测数据从图像空间映射到参数空间，获取焊缝缺陷的几何信息。然而，Hough变换需要将成像得到的图像空间映射到三维参数实施参数计算，参数个数越多，映射的维数越大，计算量也会相应地增加，实时性较差，不适合在实际工程中推广和应用[8-9]。

基于以上背景，提出一种基于线性矩阵求解的焊接缺陷几何量精确定征技术，通过对焊接缺陷超声TOFD检测成像的特点进行分析研究，建立超声TOFD图像的解析模型，在此基础上构建线性方程组，将原本非线性的参数估计问题转换成线性的矩阵求解问题，提高问题求解的效率，为开展实际的工程应用奠定理论基础。

1 超声TOFD检测图像参数化建模

超声TOFD的D扫描成像检测原理如图1所示，由于超声TOFD换能器所产生的声场扩散角的存在，当换能器处于A位置时，检测得到的扫描信号为Xn-1，当探头扫描至下一位置B处时，缺陷上端正好处于两换能器连线的中垂线上，检测到的扫描信号为Xn，而当换能器扫描至位置C时，检测到的扫描信号为Xn+1。在这些信号中，Xn才是有用信息，可以用于确定缺陷的端部深度位置以及缺陷的横向位置，其余的扫描信号都属于冗余信息。由于缺陷在两换能器中间位置时的声程最短，而当换能器远离缺陷时声程又随之变长，因此超声TOFD检测图像中的缺陷端点呈现明显的双曲线特征，缺陷位置信息及尺寸信息难以直接从图中准确获取。

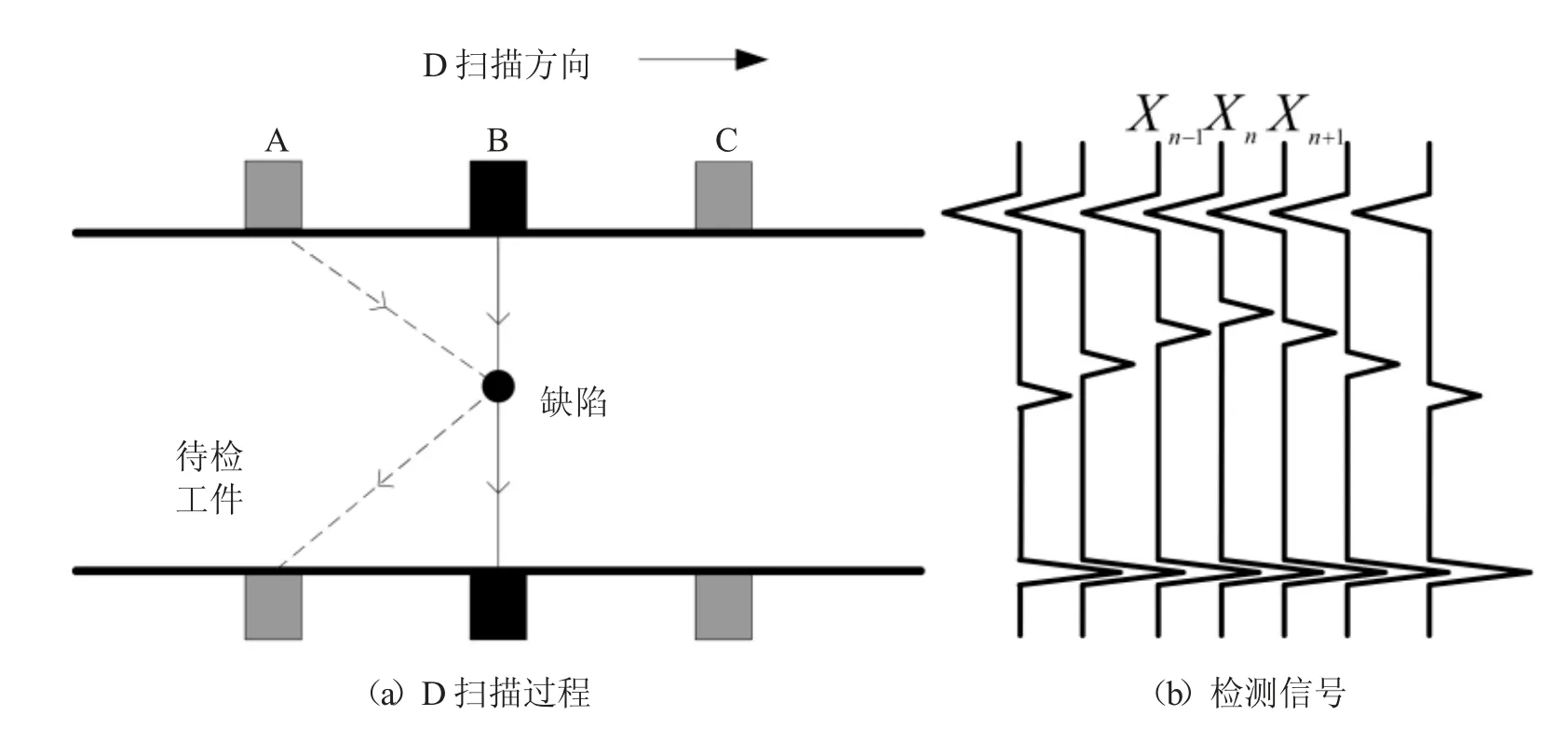
图1 超声TOFD检测D扫描原理示意图

如图2所示，将换能器分别放置于焊缝两侧，在被检工件表面上沿着焊缝所在的方向移动即可实现D扫描成像检测。换能器在移动过程中，缺陷衍射波的渡越时间会随着换能器与缺陷之间的相对位置的变化而变化。渡越时间的计算公式可表示为

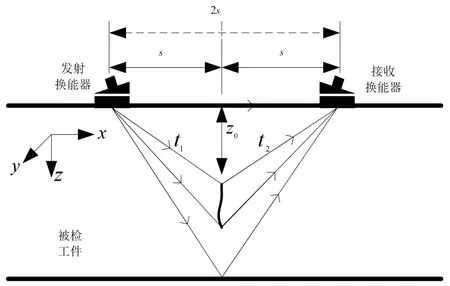
图2 超声TOFD检测D扫描示意图

式中y0表示缺陷的y坐标位置。由式（2）可知，超声TOFD检测D扫描图像所对应的解析表达式为双曲线函数。可见，为获取缺陷在工件中的几何量信息，就需要精确估计参数y0、m以及cL。

2 线性矩阵模型参数求解算法

最小二乘法是用于参数拟合估计最为常用的方法[10-11]，比如牛顿迭代法，然而该方法对初始值较为敏感，若初始值不合适，系统很有可能会出现不收敛或者收敛的情况[12]，因此可靠性不高。为此，本文通过对双曲线方程进行改写，构建出线性矩阵方程组，将最小二乘法所对应的非线性问题转换成线性方程组进行求解，以此来提高参数求解的可靠性。将式（2）中的双曲线方程改写为如下所示的二阶多项式，即

式中

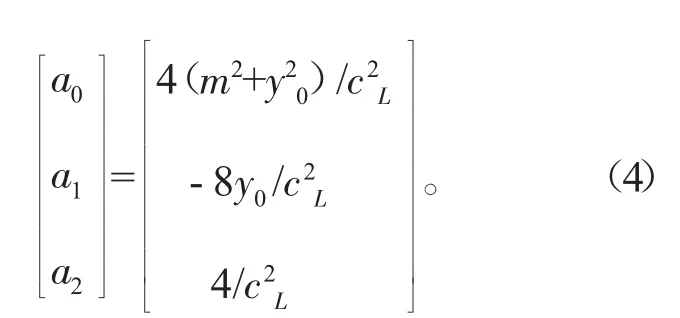
上述线性矩阵模型中参数的求解可归纳为一个参数优化的问题，因此需要构建一个合适的优化目标函数J，此处将目标函数设定为代数距离。以代数距离作为目标函数，J可表示为

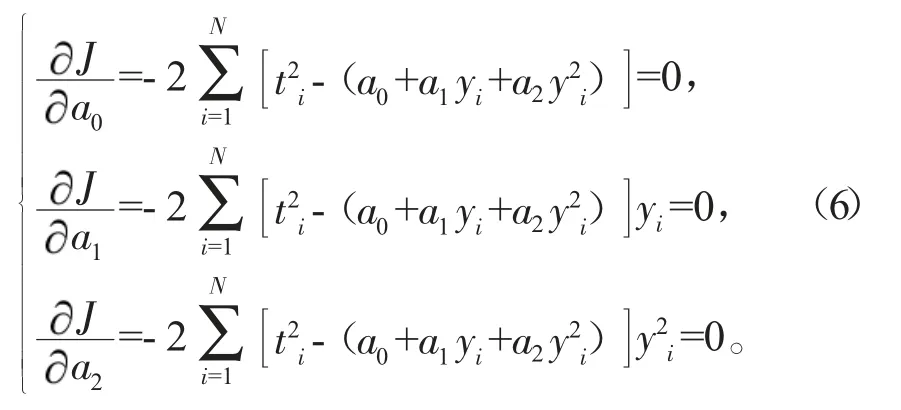
对式（6）进行进一步处理，可得

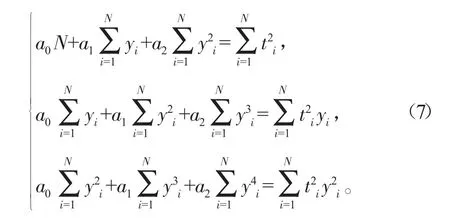
为便于后续的计算，可将式（7）转换为

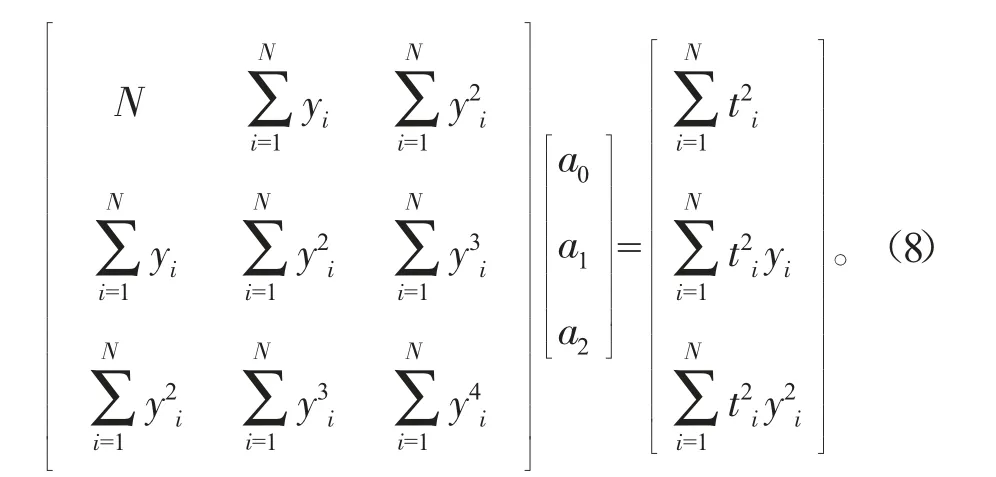
上式可简单表示为矩阵的一般表达式

根据以上推导可知，只要根据实际检测数据获取矩阵Y和P，便可以利用式（8）所示的线性矩阵方程求解出系数a0、a1和a2。然后再利用式（4）所示的线性矩阵方程组求解出未知参数cL、y0以及m。

3 仿真与实验研究

3.1 仿真研究

根据式（4），设定双曲线模型的参数m=30、cL=6和y0=30，可得

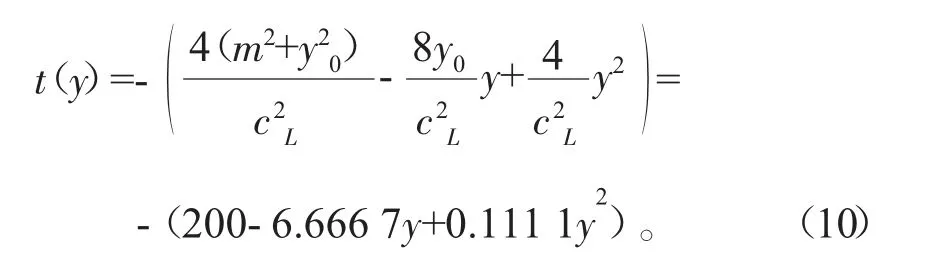
利用式（10）所给出的函数绘制如图3（a）中实线所示的双曲线图形。结合实际情况，由于检测过程中受到检测环境等因素的影响，检测信号通常都会存在一定程度的误差，因此可在仿真数据中加上一些随机扰动，作为原始的检测数据使用，如图3（a）星号点所示。在这些仿真的原始数据的基础上，结合本文所提的算法对模型参数进行估计，其估计结果如图3（b）所示。由图3可以看出：根据估计的参数所描绘出来的曲线与原始曲线基本一致，该方法具有较高的可靠性和计算精度。

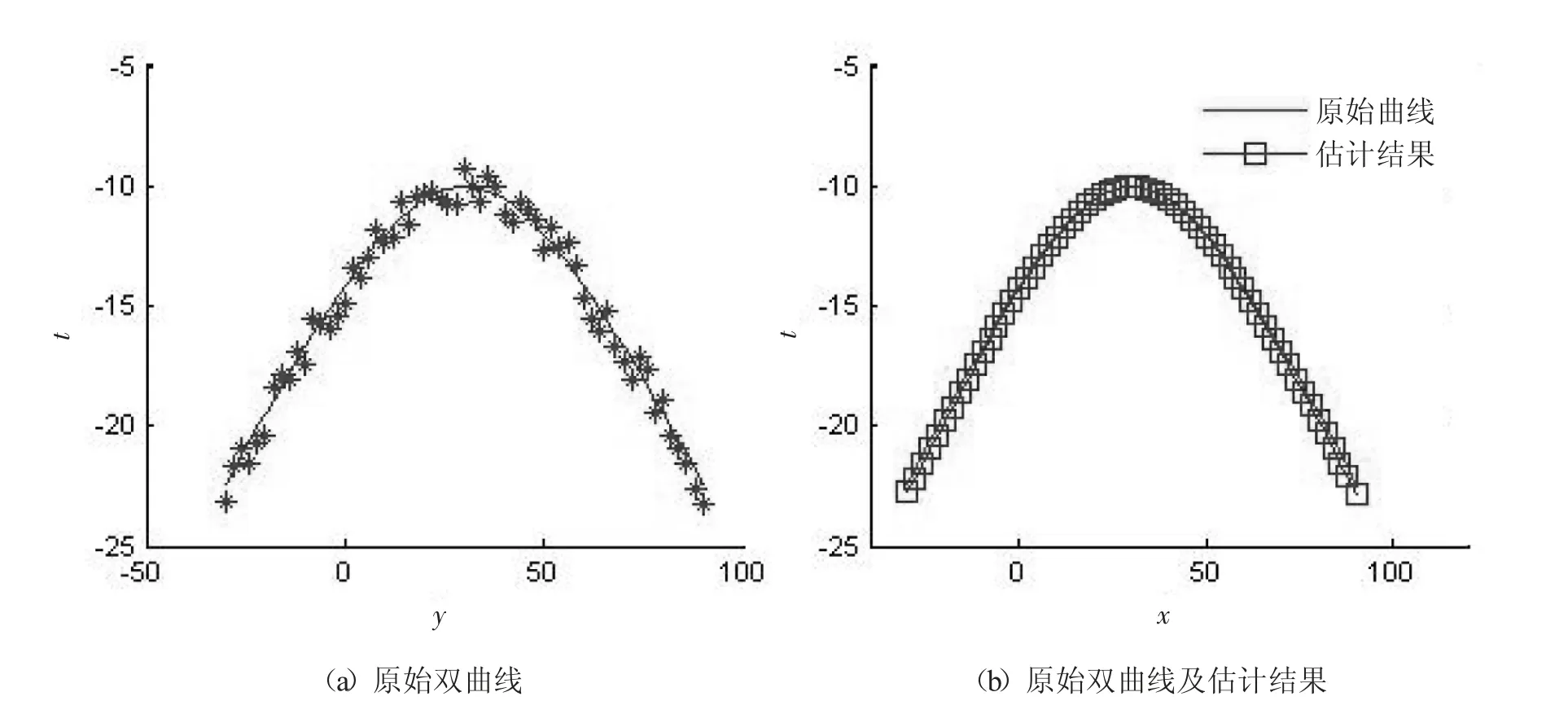
图3 双曲线参数估计仿真结果

为了进一步验证本文算法的有效性，分别采用Hough变换和遗传算法对模型参数进行估计，并将参数估计结果进行比较分析，从精度及效率两个方面进行比较评判。利用Matlab软件开展分析，所用的电脑配置CPU为Intel（R）Core（TM）i7-8550U，主频为2.00 GHz。分析结果如表1所示：所用的3种方法估计结果的误差均小于5%，都具有较高的估计精度，其中本文算法所得的结果精度与遗传算法较为接近，但是所消耗的时间却只有后者的千分之一，具有较高的实时性。虽然Hough变换具有更高的计算精度，但是在计算精度提高并不明显的情况下计算效率却远远低于本文算法。结果表明：本文算法在效率与精度的综合性能方面具有明显的优势，其综合性能较优，更适合于实际的工程应用。

表1 双曲线参数估计结果

3.2 实验研究

本文所用的超声TOFD成像检测实验平台如图4所示，该实验平台主要由超声TOFD换能器、超声发射/接收模块、机械扫查机构、A/D采样模块以及工控机等所组成。超声换能器与超声发射/接收模块相连接，用于检测信号的发射和接收，机械扫查机构可带动超声换能器实现对工件的扫查。扫查机构利用步进电机驱动，其位置信息通过编码器获取，在检测信号采集过程中，采样频率设定为100 MHz。检测信号和对应的扫查位置信息实时地传输给工控机。超声TOFD检测过程中所采用的工艺参数都根据美国ASTM标准E2373-04进行设置。

图4 超声TOFD检测平台

实验所用的超声TOFD换能器的中心频率为5 MHz、折射角为60°、晶片直径为6 mm，所用试块结构如图5所示，厚度为35 mm，包含4个垂直于底面，直径为2 mm的平底孔，孔间距30 mm，平底孔底面到工件上表面的距离分别为10 mm、15 mm、20 mm和25 mm，采用材料为45#钢。换能器中心距设定为75 mm，扫描步距为0.5 mm。为便于后续描述，将平底孔作如下定义，距离上表面10 mm的平底孔为1号缺陷，距离上表面15 mm的平底孔为2号缺陷，距离上表面20 mm的平底孔为3号缺陷，距离上表面25 mm的平底孔为4号缺陷。

图5 实验所用的试块结构图

扫查机构带动超声换能器以0.5 mm步距沿垂直于横通孔缺陷的轴线方向移动，在每个步距点得到一个A扫描信号，实现对缺陷的D扫描。利用各步距点的A扫描原始信号得到B扫查图像，被检工件试块的D扫描图像如图6所示，试块中共包含了4个平底孔缺陷，每个平底孔缺陷在超声TOFD检测图像中所呈现出的是一条双曲线。表2所示的是利用本文算法得到的缺陷几何量信息与缺陷真实几何量信息之间的误差比较，根据分析可知其测量误差均在5%以内。实验结果表明：本文算法可以根据超声TOFD检测图像准确地获取缺陷的几何量信息，满足缺陷几何信息的精确测量的要求。

图6 试块D扫描图像

表2 实测结果

4 结论

在超声TOFD检测过程中，所用超声换能器大扩散角声束所产生的冗余检测信息，使得超声TOFD检测D扫描图像中出现明显的双曲线特征，导致很难直接从检测图像中精确地获取焊接缺陷的位置及尺寸等几何信息，阻碍了缺陷自动化识别技术的发展，限制了该技术在焊缝几何量信息精确定量化中的应用。为此，提出了一种基于线性矩阵求解的焊接缺陷几何量定征技术。为验证该算法的可行性和有效性，利用包含不同深度平底孔缺陷的钢板开展实验研究，计算结果误差均在5%以内，而且较现有的优化算法有更高的计算效率，表明该算法在保证有较高精度的情况下还具有较高检测效率和综合性能，同时具有较高的实用性。