光滑床面薄层水流水动力特性试验研究
2022-10-19施明新朱永杰吴发启
施明新,朱永杰,吴发启
(1.上海勘测设计研究院有限公司,上海 200434; 2.西北农林科技大学 资源环境学院,陕西 杨凌 712100)
1 研究方法
1.1 试验设计
(1)试验装置。 试验装置包括泵站、蓄水池、消能池、稳流前池、水槽、稳流尾池、尾门、循环水廊道、量水堰等。 其中试验水槽为采用8 mm 厚的有机玻璃板制作的长6.0 m、宽0.5 m、深0.3 m 的矩形水槽,其边壁光滑、坡角可在0°~15°范围内任意调节。
(2)试验坡度(i)。 为便于探究缓坡光滑床面条件下坡度的微小变化对坡面薄层水流水动力学参数的影响,并为进一步深入研究不同下垫面坡面(如覆土坡面、自然坡面等)水流试验奠定基础,设置了0.005 8、0.011 7、0.017 5、0.023 2、0.029 2、0.034 9、0.040 7、0.046 6、0.052 4、0.058 2、0.064 1、0.069 9、0.075 7、0.081 7、0.087 5、0.105 1、0.122 8、0.140 5、0.158 4、0.176 3、0.194 4、0.212 6 等共22 级坡度(坡角在0°~5°范围内每增大20′设置1 级、在5°~12°范围内每增大1°设置1 级)。
(3)试验流量。 根据侵蚀性降雨特征和坡面径流特性[10-11],设计了6 级单宽流量,分别为0.04、0.08、0.12、0.16、0.20、0.24 L/(s·m),对应雨强分别为0.5、1.0、1.5、2.0、2.5、3.0 mm/min。 各级流量与各级坡度进行组合,共进行了132 组试验。
(4)观测断面。 共布设观测断面4 个,第1 个观测断面设置在距水槽进口1 m 处,按断面间距为1 m依次设置第2、3、4 个观测断面。
1.2 试验测定方法
通过调节供水系统阀门来控制试验流量,每种工况试验时向水槽提供稳定流量,采用60°三角形薄壁堰在水槽尾部核定流量。 在每种工况试验开始和结束时,记录稳流槽中水银温度计(精度为0.1 ℃)示数,用温度平均值计算本次试验的水动力黏滞系数。 采用SX40-1 型水位测针(精度为0.01 mm)测算水深,采用染色剂法测量坡面流流速,同一观测断面均在左侧、中间、右侧测取3 个流速和水深值,取平均值为该断面的表层流速和水深。 参照Gang 等[12]提出的方法对表层流速进行修正后得到断面平均流速,层流、过渡流、紊流的修正系数分别为0.67、0.70、0.80。 由于坡面薄层水流水深小(毫米级)且影响因素众多,难以通过试验测量获取真实值(试验过程中用测针测量的水深波动较大、误差不稳定),因此分析所用断面平均水深根据单宽流量与平均流速来计算(h=q/v,其中h为平均水深、q为平均单宽流量、v为平均流速),计算的平均水深范围为0.506~2.280 mm。
1.3 水力学特征参数计算方法
一般而言,缓流、层流的紊动作用弱,对坡面土壤层和颗粒物的剥蚀、输移能力不强,即侵蚀能力和强度均较小;而急流、紊流则相反,具有较大的侵蚀力和侵蚀强度。 依据坡面流水动力学参数进行坡面流流态、流型判别,有助于更深入认识水流对坡面物质和土壤颗粒的冲刷和侵蚀机理。 常用的坡面流水动力学参数有平均流速(v)、雷诺数(Re)、弗劳德数(Fr)、阻力系数(f)、水流功率(ω)等。
黑龙江农垦齐齐哈尔管理局依安农场始建于1956年,耕地8.5万亩,人口5000多人。经过60多年几代农场人的艰苦奋斗,如今农业结构调整基本到位,城镇建设管理日趋完善,职工生活水平普遍高于区域平均水平,打造富裕、文明、和谐、亮丽的花园式农场初步实现,先后获得国家生态示范区、省优美城镇、省平安农场、省级文明单位、省优秀企业等多项荣誉。
(1)雷诺数。 雷诺数是表征薄层水流水动力特性的基本参数,可用于判别流体是层流还是紊流(湍流):当雷诺数较小时为层流,黏滞力的作用大于惯性力的作用,黏滞力对流体质点的运动有阻碍作用;雷诺数较大时为紊流,惯性力的作用大于黏滞力的作用,惯性力对流体质点的运动有推动作用。 雷诺数计算公式为

式中:v为平均流速,m/s;R为水力半径,m;υ为水流运动黏滞系数,m2/s。
在本试验条件下,水面宽远大于水深,因此水力半径约等于水深(h),故雷诺数计算公式可改为
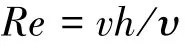
本试验为光滑床面水流试验,没有其他介质的汇入,水流为清水,因此试验条件下水流运动黏滞系数仅与水温有关,计算公式为
υ=0.017 75/(1+0.033 7t+0.000 22t2)
式中:t为水温,℃。
(2)弗劳德数。 弗劳德数可用于判别水流是急流还是缓流,计算公式为

式中:g为重力加速度,m/s2。
(3)阻力系数。 阻力系数是研究坡面流水动力特性不可或缺的参数,计算公式为
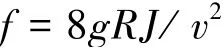
式中:J为水力坡度,对于均匀流可取地面坡度,即J=i。
(4)水流功率。 水流功率表征一定高度的水体顺坡流动时具有的势能[13],计算公式为
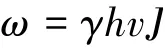
式中:γ为水的容重,kg/m3。
2 试验结果分析
2.1 平均流速与坡度和单宽流量的关系
流速大小直接影响坡面流侵蚀能力。 对于薄层水流而言,流速主要受坡度和流量的影响。 试验结果表明:平均流速与坡度关系密切,随坡度的增大而增大;平均流速随单宽流量的增大也明显增大,当坡度较小时不同单宽流量的平均流速差异较小,即单宽流量对平均流速影响较小,坡度越大流速变化越显著且流量对流速的影响越大。 江忠善等[14]认为可以用坡度和单宽流量的幂函数来计算平均流速,即v=Kqmin(式中K、m、n均为常数),据此对流速与单宽流量和坡度的关系进行幂函数拟合,结果如下(R2为决定系数):
V=1.49q0.437i0.449(R2=0.955)
2.2 雷诺数与坡度和单宽流量的关系
在本试验条件下坡面流主要处于层流区和过渡流区,流量不变时雷诺数随着坡度的增大而增大,坡度相同时雷诺数随着单宽流量的增大而增大,原因是单宽流量增大时水流惯性力逐渐增强导致水流紊动性增强、雷诺数增大。 试验结果表明,单宽流量对雷诺数的影响较坡度的影响大,且单宽流量较小时坡度对雷诺数的影响较小、单宽流量增大时坡度对雷诺数的影响逐渐增强。 对雷诺数与单宽流量和坡度的关系进行幂函数拟合,结果如下:
Re=2 413q0.757i0.357(R2=0.972)
2.3 弗劳德数与坡度和单宽流量的关系
试验结果表明,弗劳德数随着单宽流量和坡度的增大呈增大趋势。 在本试验条件下坡面流流型以急流为主,只有坡角小于2°时坡面流才可能出现缓流或临界流。 依据132 组试验数据,对弗劳德数与单宽流量和坡度的关系进行幂函数拟合,结果如下:
Fr=11.705q0.337i0.481(R2=0.948)
2.4 阻力系数与坡度和单宽流量的关系
坡面流受到的外部摩擦阻力和内部质点紊动阻力的总和称之为坡面流阻力[15]。 床面粗糙程度、断面特性、水体密度、表面张力、水流流态等因子对坡面流阻力的综合影响用阻力系数表示。 本研究由平均流速计算的阻力系数,可反映整个光滑床面的平均阻力[16]。依据132 组试验数据,对阻力系数与单宽流量和坡度的关系进行幂函数拟合,结果如下:

由上式中单宽流量和坡度的指数大小可知,坡度对阻力系数的影响很小,而单宽流量对阻力系数的影响较大。 为进一步探究单宽流量与阻力系数之间的关系,对各级坡度坡面流阻力系数与单宽流量的关系进行幂函数拟合,结果(见表1)表明:坡面流阻力系数随单宽流量的增大呈幂函数形式减小,坡角≤5°时单宽流量对阻力系数的影响较为显著且决定系数均在0.96以上;随着坡角的增大,单宽流量对阻力系数的影响逐渐减小,特别是在坡角≥10°时单宽流量对阻力系数的影响显著减小且决定系数也显著减小。 其原因可能是坡度较大时,随着坡度的增大,流速急剧加快、水流能量显著增大、水深变浅,使得水流阻力迅速增大,单宽流量不再是阻力系数的主要影响因素,而坡度对阻力系数的影响已不可忽略。
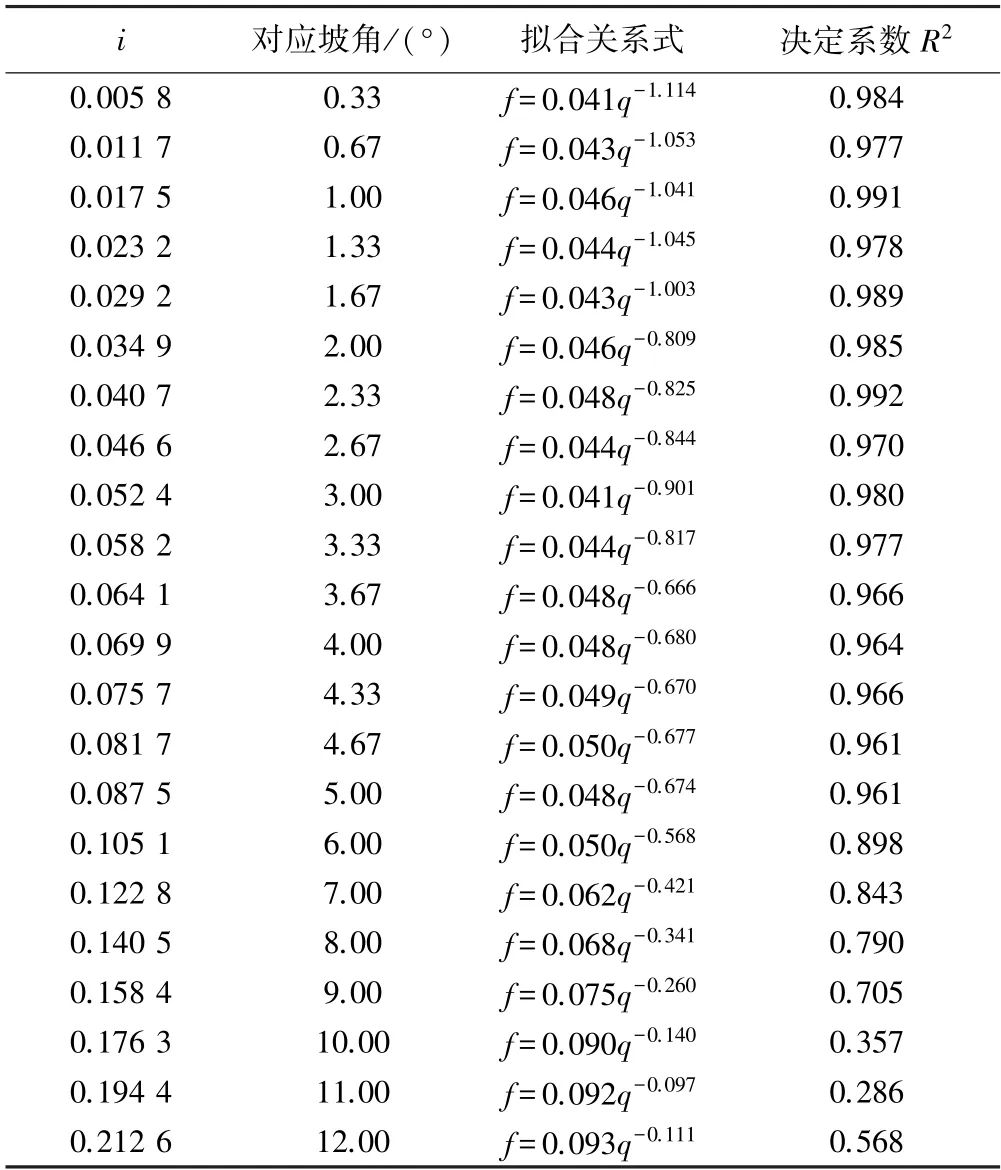
表1 各级坡度坡面流阻力系数与单宽流量的关系
2.5 水流功率与单宽流量和坡度的关系
水流功率随着单宽流量和坡度增大而增大的趋势显著,同样可用幂函数形式进行拟合:
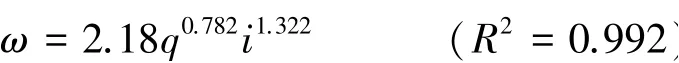
上式表明,水流功率受坡度的影响较大,受单宽流量的影响相对较小。
3 结 论
在坡角为0°~12°、单宽流量为0.04 ~0.24 L/(s·m)条件下的光滑床面水槽试验表明:坡面薄层水流雷诺数、弗劳德数、水流功率均与坡度和单宽流量呈幂函数递增关系,雷诺数受单宽流量影响较大、受坡度影响较小,坡度和单宽流量对弗劳德数的影响相当,水流功率的主要影响因素是坡度;阻力系数与坡度和单宽流量呈幂函数递减关系,单宽流量为主要影响因素、坡度为次要影响因素,坡角≤5°时坡度对阻力系数的影响可忽略不计,坡角≥10°时坡度对阻力系数的影响不可忽视;本试验条件下坡面流以急流为主,在坡角小于2°时才会出现临界流或缓流。
