基于EMD 的重力坝变形监测统计模型及应用

田紫圆，何佳楠，吴震宇，周 弭，孙 燕

（1.四川大学 水利水电学院 水力学与山区河流开发保护国家重点实验室，四川 成都 610065；2.四川天设交通科技有限公司，四川 成都 610200； 3.温州市水利局，浙江 温州 325000；4.国网四川甘孜州电力有限责任公司 康定市供电分公司，四川 康定 626000）

随着200 m 级高坝、300 m 级特高坝工程的建设运行，人们对重力坝安全监测的重要性认识不断提高。变形监测是重力坝安全监测的主要项目之一，通过开展系列重力坝变形监测模型研究，处理长时间的变形监测数据、进行变量分离和识别预测、分析安全监测资料，是对重力坝工作性态监控、异常状态诊断和安全风险评估的重要手段。

近年来随着重力坝变形监测统计模型的不断应用与发展，相关学者在改进统计模型方面已做出众多成果。 如：姚天宝等［1］针对重力坝变形监测统计模型中单一回归模型存在的不足，分别构建逐步回归分析模型和偏最小二乘回归模型，2 种模型对重力坝变形监测结果分析均具有较好的适用性；胡明秀等［2］在重力坝坝顶垂直位移统计模型中增加新高水位因子，有效模拟了初蓄期水位变化对垂直位移带来的影响，并且分解出合理的时效发展过程。 但传统重力坝变形监测统计模型在设定水压分量、温度分量的构造形式时出现变量过多、各因子间关联性较强的问题，进而使模型精度降低，因此不少学者将主成分分析（PCA）方法融入重力坝变形监测统计模型中。 如张伟等［3］利用PCA 方法选取了4 项主成分代替原设定的12 项构造指标，进行统计模型的构建，得到良好的预测精度。 但此类模型在构建前需要对水压分量、温度分量、时效分量的因子预先做出人为设定，使统计模型各分量的分离结果受监测时段和各分量构造形式的影响，存在时效分量难以准确模拟、模型预测精度不易保证等问题。经验模态分解（EMD）是Huang 等［4］提出的一种处理非线性信号的方法，优点在于无须设定任何基函数，对非线性数据序列的处理效果明显。 目前多数学者采用EMD 方法研究有限个固有模态函数（IMF）的特性［5］，将数据序列分解为时效趋势项和周期项［6］，而较少学者将其应用于重力坝变形监测统计模型的构建。

本文以YL 重力坝9＃坝段真空激光LA9 测点为例，采用EMD 方法分解时效分量，建立基于EMD 的重力坝变形监测统计模型，另选取HTT、HST、HTpcaT 统计模型，采用不同的评价指标对4 种统计模型的精度与合理性进行对比。

1 重力坝变形监测统计模型

1.1 HTT 统计模型

HTT 统计模型由水压分量、温度分量、时效分量构成，表达式为

式中：bi为回归系数；Ti（i＝1，2，…，7）分别为观测时刻t当天、前3 d、前5 d、前10 d、前15 d、前30 d、前60 d的平均气温。

F3（θ（t）） 采用式（4）或式（5）计算：

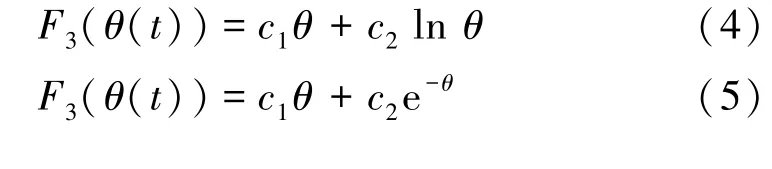
式中：c1、c2为回归系数；θ为时效因子，θ＝（t-t0）／100，t-t0为观测时刻距初始监测时刻的天数。

1.2 HST 统计模型

HST 统计模型表达式为

式中：bi（i＝1，2，…，4）为回归系数。

1.3 HTpcaT 统计模型

HTpcaT 统计模型表达式为

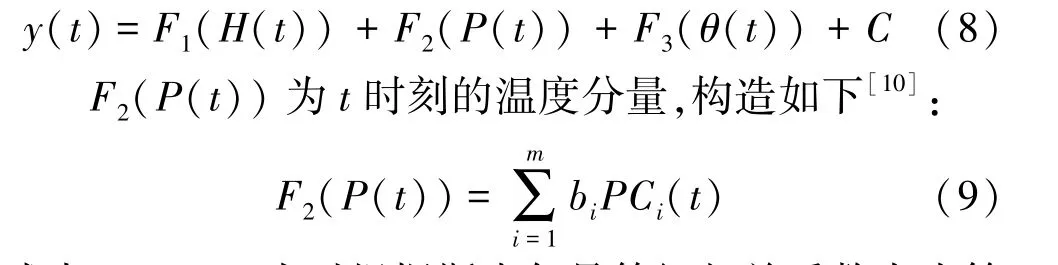
式中：PCi（t） 为对根据斯皮尔曼等级相关系数大小筛选出的坝体温度的数据序列进行主成分分析后得到的主成分因子；m为使主成分PC1、PC2、…、PCm的累计贡献率Mm大于85%或95%的主成分个数。

1.4 基于EMD 的统计模型

基于EMD 的统计模型通过EMD 方法将数据序列分解为周期项和时效趋势项，周期项由水压分量、温度分量构成，时效趋势项即为时效分量。 EMD 方法的优点是无须设定任何基函数，依据原始监测效应量的局部特征时间尺度及自身特点在筛选过程中自适应地进行分解，产生非周期性的时效分量。 其分解如下：

2 工程应用

2.1 工程概况

YL 水利枢纽主要由拦河碾压混凝土重力坝、泄洪消能建筑物、引水发电建筑物等组成，属日调节水库。YL 重力坝坝顶高程为1 334.00 m，坝顶长516.00 m，最低建基面高程为1 166.00 m，最大坝高为168.00 m，最大坝底宽度为153.20 m，坝轴线方向为北12°东，自左至右依次布置左岸挡水坝段、河床溢流坝段、右岸挡水坝段，2 个中孔分别布置在左、右侧的溢流坝段内，其中：9＃坝段长度为20.00 m，坝顶高程为1 334.00 m，建基面高程为1 186.00 m。 为了解大坝运行期间坝段顺河向水平位移，在YL 重力坝坝顶布置真空激光准直线系统，其中9＃坝段坝顶布置真空激光LA9 测点。 在9＃坝段坝体内埋设18 支温度计（分别为T1～T18），目前有14 支温度计正常在测，各温度计埋设间距约为15 m，利用温度计能够大致反映坝体内的空间温度分布情况，监测仪器布置见图1。

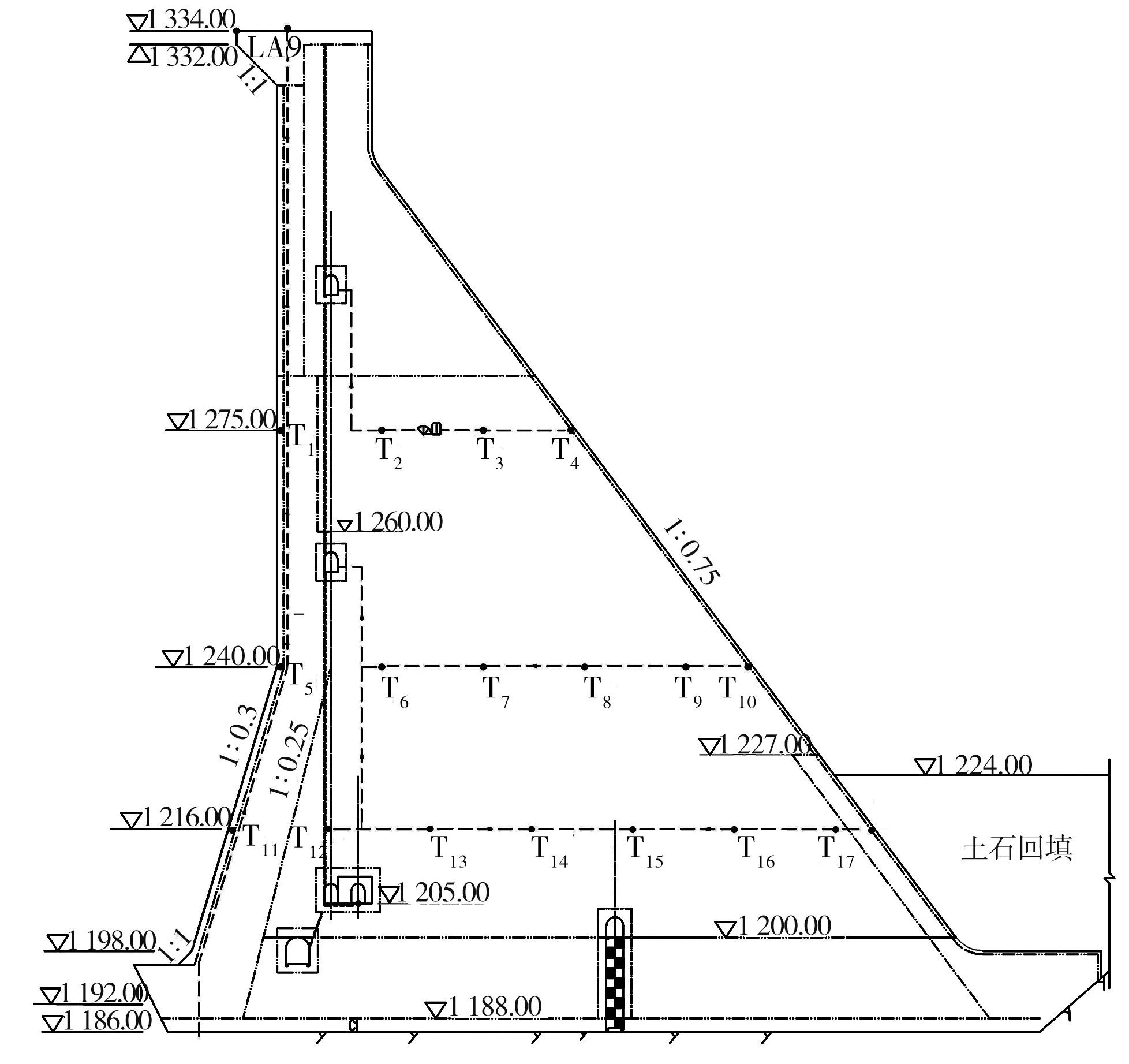
图1 YL 重力坝9＃坝段监测仪器布置（单位：m）

2.2 真空激光LA9 测点顺河向位移统计模型

采用2015 年5 月1 日—2017 年5 月1 日真空激光LA9 测点顺河向位移的观测值作为构建统计模型的样本观测值；采用最小二乘法进行多元线性回归分析，显著性水平α设置为0.05；采用2017 年5 月2日—2017 年8 月1 日的观测值作为预测集，用来检验模型的预测效果。

真空激光LA9 测点顺河向位移的HTT、HST 和HTpcaT 统计模型的时效分量均采用c1θ＋c2lnθ和c1θ＋c2e-θ的形式构造。 与HTT、HST 统计模型相比，HTpcaT统计模型的构建仅在温度分量上有所不同，其温度分量由对坝体温度进行主成分分析后得到的因子组成。选取各坝体温度与真空激光LA9 测点顺河向位移之间的斯皮尔曼等级相关系数的绝对值大于0.65 的T4、T8、T10、T14这4 支温度计，利用MATLAB 软件进行主成分分析后组成温度项，主成分PC1和PC2的累积贡献率达到99.42%，可以达到降维目的，因此HTpcaT 统计模型将主成分PC1、PC2作为温度因子，采用c1θ＋c2lnθ的时效分量构造形式。

由于HTpcaT 统计模型比HTT 统计模型的拟合程度高，因此基于EMD 的统计模型中温度分量采用主成分PC1、PC2作为温度因子，即与HTpcaT 统计模型的温度分量构造形式相同。 与HTpcaT 统计模型不同的是，基于EMD 的统计模型不需要设置时效分量的函数构造形式，直接采用EMD 方法依据原始监测效应量的局部特征时间尺度及自身特点在筛选过程中自适应地进行分解，把得到的余项作为时效分量，把其余的固有模态函数IMF 累加作为顺河向位移的周期变化。 真空激光LA9 测点顺河向位移的EMD 分解流程见图2，真空激光LA9 测点顺河向位移的EMD 分解重构见图3。针对真空激光LA9 测点顺河向位移的EMD 分解的时效分量拟合见图4，拟合的复相关系数为0.986 8，均方根误差为0.000 98，拟合效果良好，即时效分量可由此复合函数表示。 EMD 分解的周期项包含水压分量和温度分量，采用最小二乘法对周期项进行拟合，拟合效果见图5。

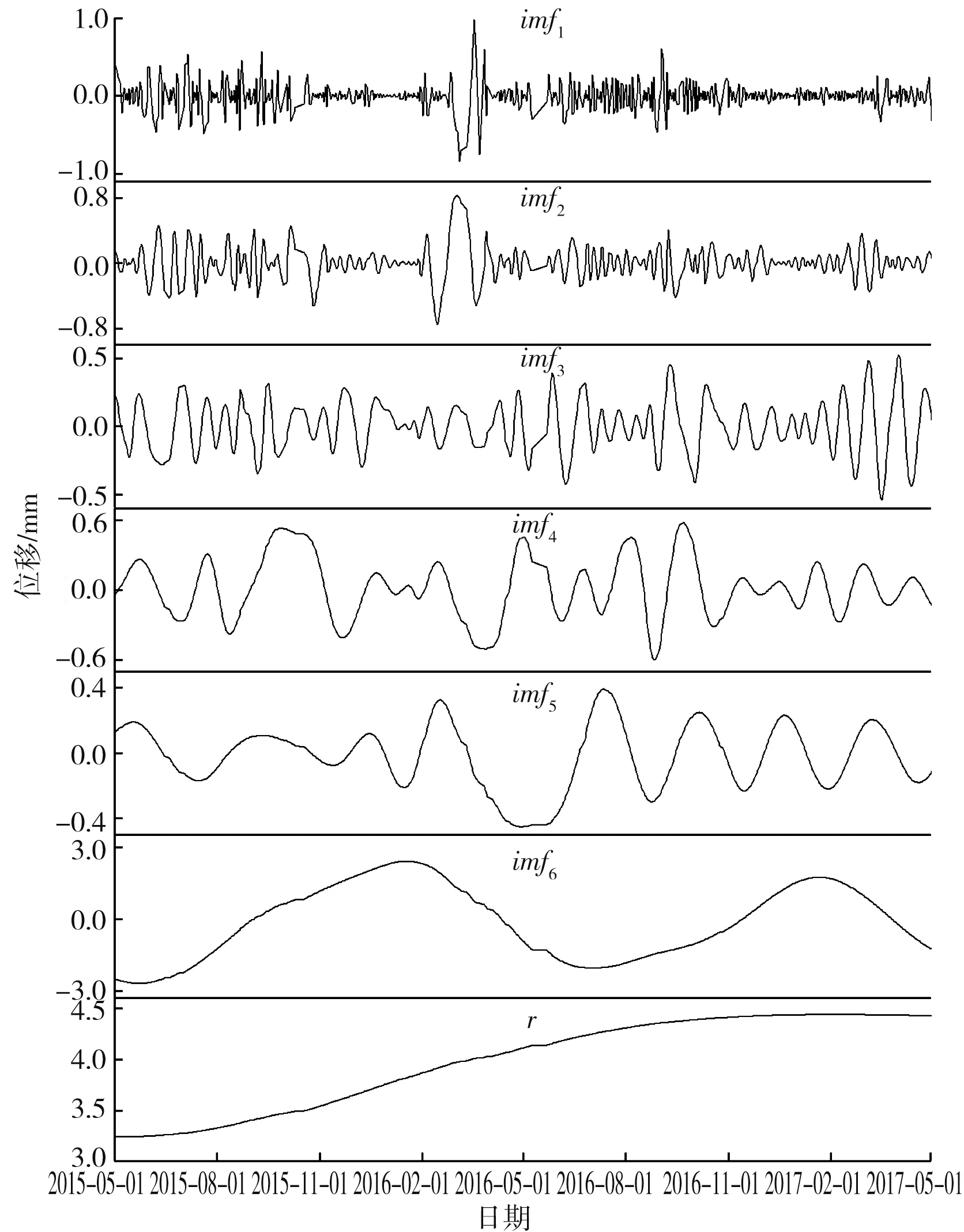
图2 LA9 测点顺河向位移的EMD 分解流程

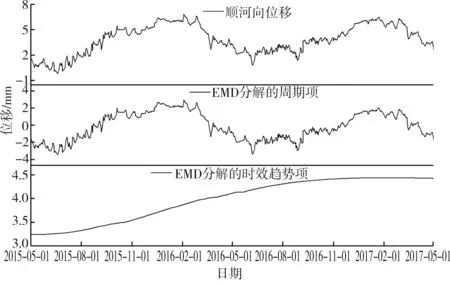
图3 LA9 测点顺河向位移的EMD 分解重构

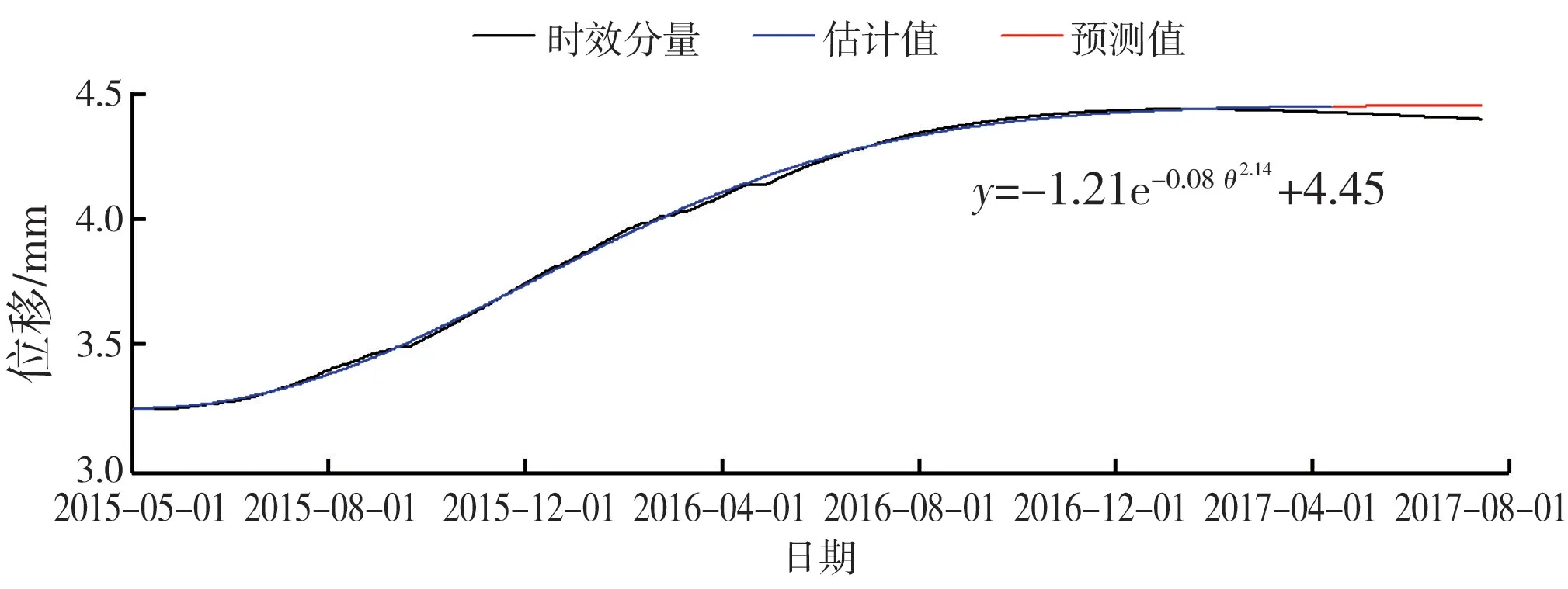
图4 EMD 分解的时效分量拟合

图5 EMD 分解重构的周期项拟合

将EMD 分解的时效分量和周期项叠加，可得到针对真空激光LA9 测点顺河向位移的基于EMD 的统计模型，该统计模型各分量的分离见图6。 在所有的影响因子中，温度分量是影响真空激光LA9 测点顺河向位移变化的主要因素，时效分量随时间增长而缓慢增大，该结果符合工程实际情况。

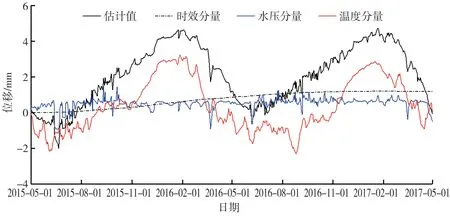
图6 基于EMD 的统计模型的分量分离

真空激光LA9 测点顺河向位移的水压分量随时间的变化见图7，水压分量与库水位的关系见图8。 水压分量与库水位具有较强的正相关性，其皮尔逊相关系数为0.94，符合工程实际情况。

图7 LA9 测点顺河向位移的水压分量变化情况

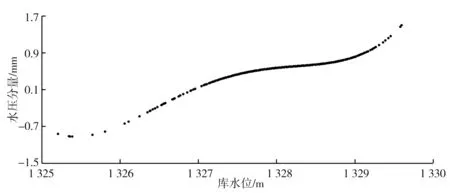
图8 LA9 测点顺河向位移的水压分量与库水位的关系

LA9 测点顺河向位移的时效分量在不同统计模型中分离的结果见图9，HTT、HTpcaT 统计模型的时效分量在选定的初始时间均出现突变，后续变化平缓。 由于对工程选取的时间段已进入稳定运行期，时效分量不应在初始时间出现突变，因此该结果与工程实际情况不符。 基于EMD 的统计模型克服了上述HTT、HTpcaT 统计模型的缺陷，未提前设置时效函数类型，时效分量由位移数据特性直接分解产生，能更好地模拟时效分量的实际变化趋势。 基于EMD 的统计模型将位移数据序列分离成周期项和时效趋势项，赋予效应量合理的物理意义，并且单独进行分量构造再叠加，使得该模型在预测结果的准确性和合理性比传统的统计模型更有优势。

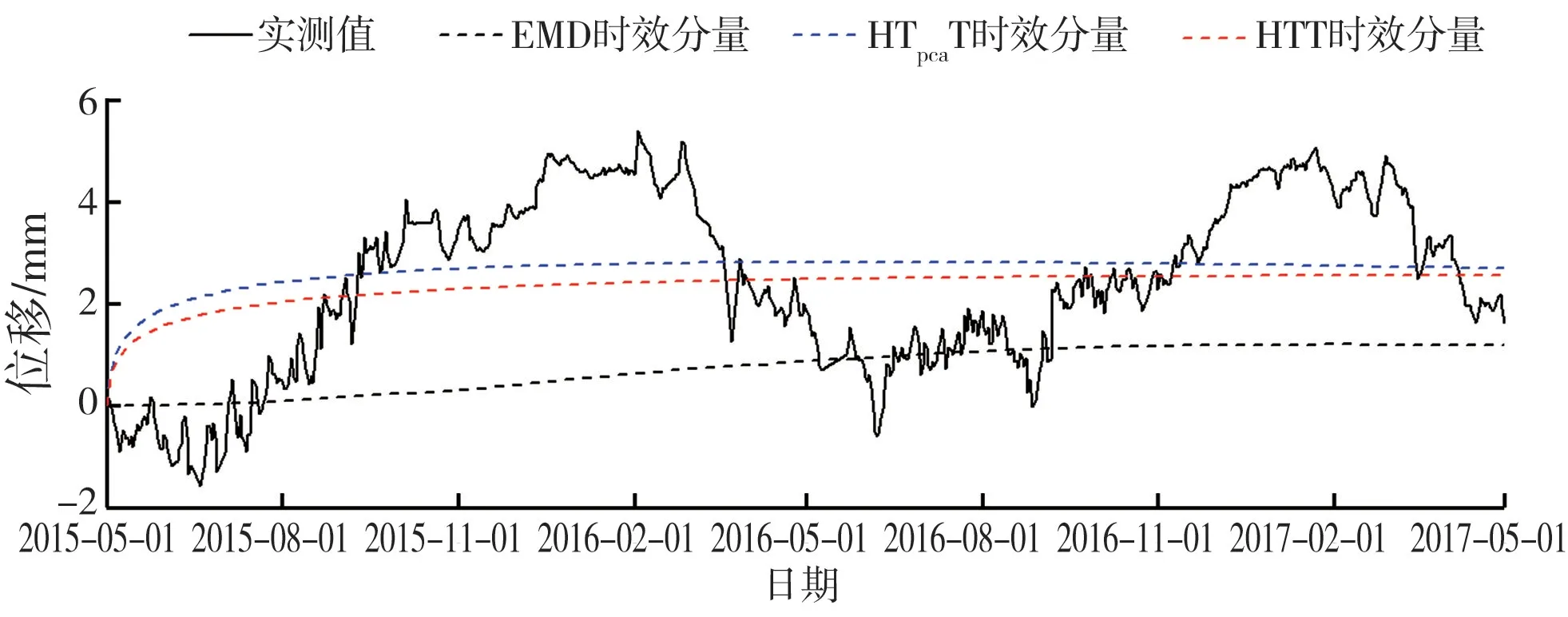
图9 LA9 测点顺河向位移的时效趋势

各统计模型应用于监测顺河向位移的评价指标值见表1，可知4 种统计模型均通过了一致性检验，R2和均为0.9 左右，拟合效果较优，回归效果显著。 基于EMD 的统计模型较传统统计模型的拟合精度略低，时效趋势在复合指数函数拟合下精度较高，其主要的拟合误差来源于重构周期项的拟合。 分析原因如下：一是重构周期项中包含了效应量自身的数据误差；二是最小二乘法默认各因子为线性关系，使用有一定局限性。 但基于EMD 的统计模型的预测精度得到了有效提升，其RMSE为0.406 mm，MAE为0.333 mm，侧面反映了基于EMD 的统计模型的物理意义更加明确以及在一定程度上能避免过拟合问题。

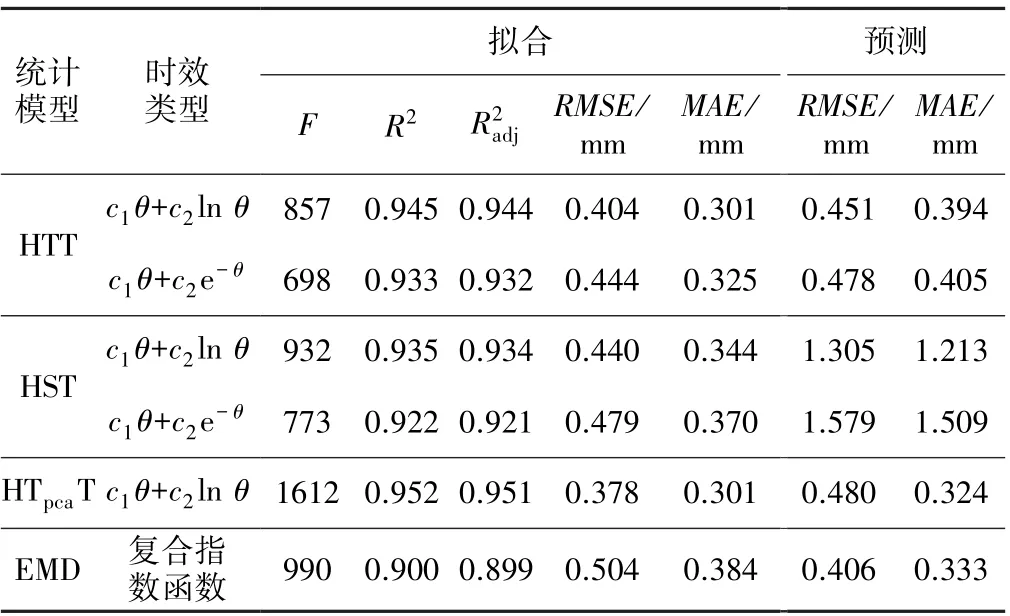
表1 各统计模型的评价指标值

3 结 论

以YL 重力坝9＃坝段位移测点为例，采用EMD 方法将数据序列分解重构成周期项和时效趋势项，使用评价指标对比不同统计模型的精度与合理性。 相比传统监测统计模型，基于EMD 的统计模型在效应量分离的准确性和合理性方面均比传统的统计模型更有优势，能更好地模拟时效分量的实际变化趋势。 但基于EMD 的统计模型在拟合时受重构周期项的误差与方法局限，拟合精度略低，今后应该仔细核对原始数据以及在拟合时考虑非线性关系，以提高拟合精度。