Ti-10V-2Cr-3Al钛合金的高温压缩变形行为及本构关系

李 聪，丁智力，陈 荐，周 幸

(1.长沙理工大学能源与动力工程学院，长沙 410114；2.清远市粤博科技有限公司，清远 511500)

0 引 言

钛合金是20世纪中叶发展起来的一种重要结构材料，具有低密度、高可调比强度、优异的耐腐蚀性、良好的低温延展性和良好的生物相容性等特点，广泛应用于航空航天、化工、军工和生物医学等领域[1-2]。研究人员一般通过调整钛合金的化学成分(目的是改变β相的转变温度和马氏体转变起始点Ms)和热变形条件(特别是应变速率和变形温度)对现有不同商用双相钛合金的力学性能、变形机制和微观结构演变进行研究[3-6]。GUPTA等[7]研究了Ti-15V-3Cr-3Sn-3Al合金在冷轧和斜轧过程中的组织和织构演变，发现应变对显微组织演变具有重要的影响。JHA等[8]研究了初始显微组织为层状和等轴状晶粒的商业Ti-6Al-4V合金的热变形行为，通过Arrhenius方程得到不同变形条件下的变形激活能，并分析了微观结构的演变。ROY等[9]对Ti-6Al-4V-0.1B合金在高温条件下变形时的微观结构演变进行了系统的阐述。MURTHY等[10]和SAGAR等[11]研究了在热机械加工过程中变形温度对α+β双相Ti-Al-Mn合金和Ti-24Al-20Nb合金微观结构和力学性能的影响。已有研究表明，在高温环境下，应变速率、变形温度等因素对显微组织局部流动、绝热剪切带、组织球化等微观结构演变具有重要影响[12]。

钛合金在热加工过程中的变形机制很复杂，因此难以准确判断其热加工性能。在不考虑材料复杂物理机制的条件下，唯象本构方程能够很好地反映热加工时变形参数与流动应力之间的关系。构建起能准确描述材料变形规律的本构方程后，即可利用该方程预测材料在高温变形时的流动应力，相比于试验研究可以节约大量时间和人力成本。一些学者[13-17]通过修正Arrhenius方程建立了不同钛合金材料的本构方程，方程的预测能力良好。在此基础上，学者们[14-19]研究了钛合金在高温变形时的应变硬化与流动软化效应，结果表明，钛合金的流动应力随着变形温度的升高而减小，随应变速率的增加而增大。

新型Ti-10V-2Cr-3Al钛合金中含有钒、铬和铝元素，增强了合金的固溶强化作用，提高了强度与塑性，扩大了β相区区间，合金的热稳定性也较高，在工业领域具有较大的应用潜力。目前，该合金在高温变形领域的相关研究很少。因此，作者通过热压缩试验研究了Ti-10V-2Cr-3Al钛合金在高温条件下的流变行为和显微组织演变，构建了合金高温变形本构模型并进行了修正。

1 试样制备与试验方法

试验材料为Ti-10V-2Cr-3Al钛合金，由中国科学院金属研究所提供，其化学成分(质量分数/%)为10.6V，2.18Cr，3.19Al，0.1O，0.05C，0.013N，0.001H。试验合金的初始显微组织为α+β双相组织，存在非常多细小的α相，并且在晶界处存在一些较粗的层状α相，如图1所示。试验合金的β相转变温度约为800 ℃[20]。通过电火花加工和线切割将Ti-10V-2Cr-3Al钛合金加工成尺寸为φ5 mm×10 mm的圆柱形试样，使用TA DIL805D型热模拟机在真空环境、α+β相区(变形温度730，790 ℃)和β相区(变形温度820，880 ℃)进行等温热压缩试验，应变速率分别为0.1，0.05，0.01，0.005，0.001 s-1。压缩试验结束后立即用氩气冷却试样，以保留热变形组织。

沿压缩方向轴向切割试样，对试样进行镶样，抛光后，采用Kroll试剂(3 mL HF+6 mL HNO3+100 mL H2O)进行腐蚀，在LF7M38型光学显微镜和JEOL型扫描电子显微镜下观察变形后的显微组织。

图1 Ti-10V-2Cr-3Al钛合金初始显微组织Fig.1 Initial microstructure of Ti-10V-2Cr-3Al titanium alloy

2 试验结果与讨论

2.1 真应力-真应变曲线

由图2可知，试验合金的真应力-真应变曲线可以分为初始阶段、转变及软化阶段和稳态流动阶段3个阶段。在初始阶段，试样受到压缩时的加工硬化作用远大于软化作用，位错密度增加，导致应力快速上升。在转变及软化阶段的前期，应力下降形成“波谷”，出现不连续屈服现象[15]，并且随着变形温度的升高或应变速率的下降，不连续屈服现象变得更明显，上屈服强度有所下降。关于钛合金的不连续屈服现象，WANJARA等[21]研究认为是高体积分数溶质原子形成Cottrell气团钉扎固溶原子造成的，而SHEIKHALI等[22]则认为是β相中间隙原子与螺型位错应力场交互作用造成的，这两种观点存在争议。动态理论[23]能够很好地解释不连续屈服现象的出现：随着变形的进行，晶界处的位错堆积达到临界值，增强了动态回复的作用，导致流动应力下降和不连续屈服现象；随着温度的升高，位错攀移更加容易，动态回复的驱动力增大，不连续屈服现象更加明显；随着应变速率的增大，位错密度增加，导致明显的不连续屈服现象。

图2 不同变形温度和不同应变速率下压缩时试验合金的真应力-真应变曲线Fig.2 True stress-true strain curves of test alloy during compression at different deformation temperatures and strain rates

此外，在转变及软化阶段，不同变形条件下流动应力下降(软化)的诱发因素不同。一般而言，当应变速率高于10 s-1时，绝热加热使得变形温度上升，导致流动应力下降[20]；而当应变速率低于10 s-1时，显微组织演变对软化起到主导作用。当变形温度一定时，高应变速率下的流动软化效应比低应变速率下的流动软化效应更强；这是因为当应变速率较高时，试样达到一定变形量所需的时间缩短，位错数量增加，位错运动[16,24-25]导致流动软化作用大于加工硬化作用。随着应变的增大，流动软化作用逐渐减弱，最终加工硬化作用与软化作用达到动态平衡，合金进入稳态流动阶段。

2.2 显微组织

由图3可以看出：当应变速率为0.01 s-1时，随着变形温度的升高，压缩后试验合金中的α相体积分数逐渐下降。在730 ℃下变形时，试验合金中的原始层状α相发生弯曲，同时存在部分球状和短棒状α相；当变形温度上升到790 ℃时，α相逐渐向β相转变，并且开始发生动态球化，α相还发生了界面迁移。由此可见，在α+β相区(730，790℃)热压缩时试验合金发生了动态球化与动态再结晶。当温度升高到高于β转变温度时，动态再结晶形核生长的驱动力更强，因此在β相区(820，880 ℃)变形时，试验合金发生动态再结晶，组织中出现了再结晶β晶粒。

3 本构方程的建立与验证

3.1 Arrhenius本构方程

(1)

(2)

(3)

式中：A，α，β，n1为材料常数；Q为变形激活能；R为气体常数，8.314 J·mol·K-1；T为热力学温度；n为与应变速率敏感性指数相关的应力指数。

当应变速率较低(ασ<0.8)时常用幂律方程，即式(1)来描述应变速率、变形温度与应力之间的关系；当应变速率较高(ασ>1.2)时常用指数方程，即式(2)来描述应变速率、变形温度与应力之间的关系。式(3)为双曲正弦方程，是适用所有条件的Arrhenius本构方程。将式(1)、式(2)和式(3)两边同时取对数，可以得到

图3 在不同变形温度、应变速率0.01 s-1下压缩后试验合金的显微组织Fig.3 Microstructures of test alloy after compression at different deformation temperatures and strain rate of 0.01 s-1

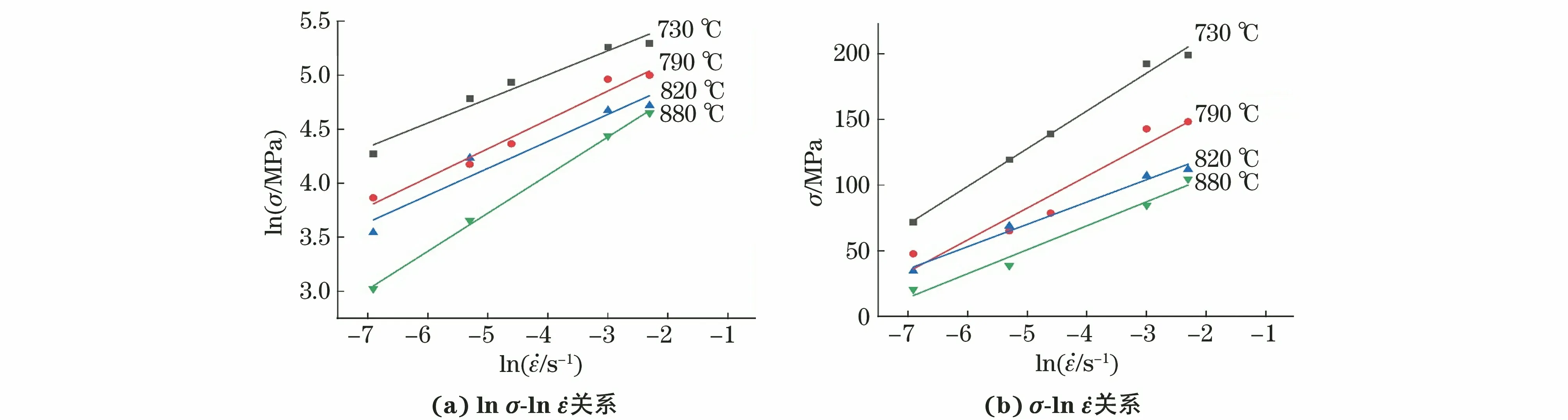
图4 不同变形温度下试验合金的真应力与应变速率关系Fig.4 Relationship between true stress and strain rate of test alloy at different deformation temperatures:(a) ln σ-ln relationship and (b) σ-ln relationship

(4)

(5)

(6)

(7)

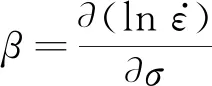
(8)

(9)

表1 不同变形温度下试验合金的Arrhenius本构方程材料常数

3.2 指数方程及其修正

3.2.1 指数方程的建立

当应变速率为0.1，0.05 s-1时，可以采用指数方程描述试验合金变形参数与应力之间的关系。应变为0.1时对应的流动应力为稳定状态，通过式(8)可以求解不同变形温度下的β值。在应变速率不变条件下，利用式(5)将真应力对1/T求偏导，得到Q值计算公式，如下：

(10)

图5 不同应变速率下试验合金σ与1/T的关系Fig.5 Relationship between σ and 1/T of test alloy at different strain rates

将Zener-Hollomon参数(Z参数)引入式(5)，得到

(11)

由式(11)可计算得到不同温度下的lnA值。将α+β相区(730，790 ℃)和β相区(820，880 ℃)本构方程的各个参数取平均值，结果如表2所示。

一般认为，金属材料在高温下的塑性变形机制可以通过计算变形激活能和观察微观结构来确定。在α+β相区、应变速率不低于0.05 s-1压缩时，试验合金的变形激活能为279.583 kJ·mol-1，远高于α-Ti(169 kJ·mol-1)[16]和β-Ti的自扩散能(153 kJ·mol-1)[27]，这表明在α+β相区的热变形是由高温扩散以外的过程，即动态再结晶、动态回复等需较高“势垒”的变形机制所控制。在β相区，软化机制为动态再结晶与动态回复，动态再结晶需要较高的变形能驱动，在变形能较低时，软化机制以动态回复为主。在β相区压缩时试验合金的变形激活能为145.967 kJ·mol-1，接近β-Ti的自扩散能，且扩散系数较高，有观点认为，当变形激活能和扩散激活能相近时，热变形受扩散相关过程控制[28]。

表2 应变为0.1时试验合金指数方程的参数值

将表2中的参数代入式(5)，即可得到在α+β相区和β相区、应变速率不低于0.05 s-1热压缩时试验合金的Arrhenius指数方程，分别如下：

(12)

(13)

将表2中的参数lnA，β，σ代入式(11)，计算得到lnZ。对lnZ和σ进行线性拟合，结果如图6所示，在α+β相区和β相区压缩时lnZ和σ的拟合相关系数R2分别为0.993和1，这表明建立的指数方程——式(12)和式(13)均具有良好的预测能力。

图6 ln Z和σ的关系Fig.6 Relationship between ln Z and σ

3.2.2 指数方程的修正

除了应变速率和变形温度，应变对本构行为也有显著影响[29]。在真应变0.04～0.38范围内，采用相同的方法计算指数方程中的β，Q，lnA等参数，应变取值的间距为0.02。β，Q，lnA和真应变ε的关系如图7所示，可见β，Q，lnA均为ε的函数。

由图7(c)可以看出：在α+β相区、应变速率不低于0.05 s-1下变形时试验合金的Q值在初期快速下降，这表明合金发生了动态再结晶形核及动态球化；随着变形量的增加，动态再结晶形核基本完成，组织变化较小，Q值达到动态平衡。β相区的变形温度高于β相转变温度，试验合金的Q值在变形前期快速下降，在应变为0.1左右达到最低点，如图7(d)所示，这表明合金发生了动态再结晶。β相区的软化机制主要为动态再结晶与动态回复。动态回复会使变形激活能接近纯钛的自扩散活化能[30]，再加上变形量增加等多重因素的影响，因此应变大于0.1时变形激活能增加。

图7 α+β相区和β相区指数方程各参数与应变之间的关系Fig.7 Relationship between each constant and strain of exponential equation in α+β (a,c,e) and β (b,d,f) phase regions

材料常数受应变影响较大，因此为了提高本构方程预测的准确性，采用多项式对各材料常数和应变进行拟合，拟合多项式分别如下：

β=B3ε3+B2ε2+B1ε+B0

(14)

Q=Q3ε3+Q2ε2+Q1ε+Q0

(15)

lnA=A3ε3+A2ε2+A1ε+A0

(16)

式中：B0～B3，Q0～Q3，A0～A3均为拟合系数。

拟合得到的系数见表3。联立式(14)～(16)和式(5)，并代入表3中的系数，即得到修正的指数方程。

3.3 双曲正弦方程及其修正

3.3.1 双曲正弦方程的建立

当应变速率为0.001～0.01 s-1时，可以采用双曲正弦方程描述试验合金的本构关系。由表1可以得到在α+β相区和β相区α的平均值分别为0.009 37和0.017 4。对式(6)求偏导可以得到

(17)

(18)

表3 在α+β相区和β相区压缩时β，Q，ln A和ε三阶方程的参数值

(19)

利用式(19)计算出lnA值。应变为0.1时试验合金双曲正弦方程各参数值列于表4。在α+β相区和β相区压缩时试验合金的变形激活能分别为290.190，266.815 kJ·mol-1，均远大于α-Ti和β-Ti的自扩散能，这说明合金的软化机制为动态再结晶。

图和ln[sinh(ασ)]-1/T关系Fig.8 Relationship between ln[sinh(ασ)]-ln and ln[sinh(ασ)]-1/T

表4 应变为0.1时试验合金双曲正弦方程的参数值

将表4中的参数代入式(6)，即可得到在α+β相区和β相区热压缩时试验合金的Arrhenius双曲正弦方程，分别如下：

(20)

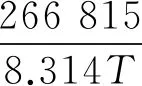
(21)

将表4中的参数代入式(19)，计算得到lnZ。对lnZ和ln[sinh(ασ)]进行线性拟合，结果如图9所示。在α+β相区和β相区压缩时lnZ和ln[sinh(ασ)]的拟合相关系数R2分别为0.82，0.95，这表明建立的双曲正弦方程——式(20)和式(21)均具有良好的预测能力。

图9 ln Z与ln[sinh(ασ)]之间的关系Fig.9 Relationship between ln Z and ln[sinh(ασ)]

3.3.2 双曲正弦方程的修正

在真应变0.04～0.38范围内，采用相同的方法计算双曲正弦方程中的相关常数(α，n，Q，lnA)，应变取值的间距为0.02。应变速率敏感系数m能够很好地反映材料是否发生超塑性行为[31]，其值等于1/n1。α，n，Q，lnA，m和ε的关系如图9所示，可见α，n，Q，lnA，m均为ε的函数。

由图10(a)可知：随着应变的增加，n值减小；在β相区压缩时，n值在2.5左右，说明试验合金受到了晶界滑动机制和位错黏滞滑移机制的共同作用[32-33]；在α+β相区压缩时，n值在3左右，说明试验合金的变形机制主要为位错黏滞滑移机制[32-33]。由图10(b)可知，两个相区的α值均随应变的增加而增大。由图10(c)可知：在α+β相区和β相区变形时试验合金的变形激活能随着应变的增加而减小。对比图10(c)和图10(d)可知，lnA与Q值随应变的变化规律基本一致。由图10(e)可知：在α+β相区压缩时，试验合金的m值随应变的增加下降明显，表明在该相区压缩时的塑性较差；在β相区压缩时的m值高于在α+β相区压缩时，且不同应变下的m值均大于0.3，试验合金表现出了超塑性。

采用多项式对双曲正弦方程各材料常数和应变进行拟合，拟合多项式分别如下：

α=X3ε3+X2ε2+X1ε+X0

(22)

(23)

Q=Q3ε3+Q2ε2+Q1ε+Q0

(24)

图10 双曲正弦方程各参数与应变之间的关系Fig.10 Relationship between parameter and strain of hyperbolic sine equation

lnA=A3ε3+A2ε2+A1ε+A0

(25)

拟合得到的各系数见表5。将式(22)～式(25)插入式(19)中，对原始双曲正弦方程进行修正。一旦获得材料常数，流动应力可通过如下具有Zener-Hollomon参数的本构方程预测：

(26)

表5 在α+β相区和β相区压缩时α，n，Q，ln A与ε三阶方程的参数值

3.4 本构方程的验证

为了验证本构方程的准确性，将试验应力和预测应力进行比较，应变速率为0.1～0.05 s-1采用修正的指数方程进行预测；应变速率为0.001～0.01 s-1时使用修正的双曲正弦方程进行预测。由图11可以看出：Ti-10V-2Cr-3Al钛合金的真应力-真应变预测曲线与试验曲线基本吻合；相对而言，在α+β相区，预测曲线与试验曲线有很好的一致性，在β相区，试验曲线与预测曲线的一致性略差，尤其是在880 ℃/0.01 s-1条件下出现了较大差异，这可能是试验误差，也可能是操作失误所致。

图11 试验合金真应力-真应变预测曲线和试验曲线的对比Fig.11 Comparison between true stress-true strain prediction curve and test curve of test alloy

由图12可以看出，试验流动应力与预测流动应力均位于10%误差带，平均相对误差为5.36%，这表明修正之后的本构方程具有良好的预测能力。

图12 试验流动应力与预测流动应力关系Fig.12 Relationship between test flow stress and predicted flow stress

4 结 论

(1) 在变形温度730～880 ℃、应变速率0.1～0.001 s-1条件下压缩时，Ti-10V-2Cr-3Al钛合金的真应力随着应变速率的增加或变形温度的降低而增大；当应变速率为0.01 s-1时，在α+β相区压缩后试验合金中出现球状和短棒状α相，软化机制为动态球化和动态再结晶，在β相区压缩后出现了再结晶β晶粒，软化机制为动态再结晶。

(2) 当应变速率为0.1～0.05 s-1时，可以采用修正后的Arrhenius指数方程描述试验合金的流变行为，而应变速率为0.01～0.001 s-1时，可采用修正后的双曲正弦方程来描述合金的流变行为；由修正方程预测得到的流动应力与试验测得的应力的平均相对误差为5.36%，说明修正的本构方程对Ti-10V-2Cr-3Al钛合金在高温环境下的流变行为具有良好的预测能力。