基于体积比模型的混合不确定可靠度计算方法
2022-10-19宋利锋陈振鸣
宋利锋,陈振鸣
(1.中国长峰机电技术研究设计院,北京 100854;2.北京航天情报与信息研究所,北京 100854)
近年来,随着工业技术的不断发展,工程结构系统中存在大量不确定信息,按不确定因素的产生机理和物理意义的不同,可分为随机性,模糊性和未确知性。在过去几十年中,基于概率统计和模糊数学逐渐建立起了2 种重要的可靠性理论——随机可靠性和模糊可靠性[1-5]。近些年来,随着国内外学者对非概率的研究,也建立了相应的非概率可靠性模型[6-8]。
本文基于一种非概率干涉可靠性模型,即用结构安全域的体积与基本区间变量域的总体积之比作为结构可靠性度量的模型[9],推导了随机变量,模糊变量和区间变量两两混合的结构可靠度计算方法,拓广了此非概率干涉模型的应用范围,可用于计算工程中存在混合不确定信息的问题,其表达明确,应用简便,有很好的实际意义。实例计算验证了方法的有效性和可行性。
1 可靠度计算
在机械结构的可靠性分析中,结构的功能函数可表示为

式中:R,S 分别为结构的广义强度和广义应力,可为其他基本变量的函数。当R,S 均为随机变量时,可用常规的概率可靠性模型求解。在此考虑其他不确定变量组合情况下的可靠度计算,将随机-区间、随机-模糊、模糊-模糊和模糊-区间几种混合模型转化为区间-区间模型,基于体积比的非概率可靠性模型,建立了相应的可靠度计算方法。由于体积比可靠性模型是建立在应力-强度干涉的条件下,所以以下问题均在应力-强度存在干涉的条件下进行讨论。
1.1 均为区间变量的可靠度计算

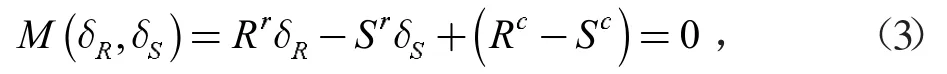
式(3)为标准化变量空间中的失效平面。
将应力和强度转换成标准化区间变量空间的应力-强度干涉关系如图1 所示。
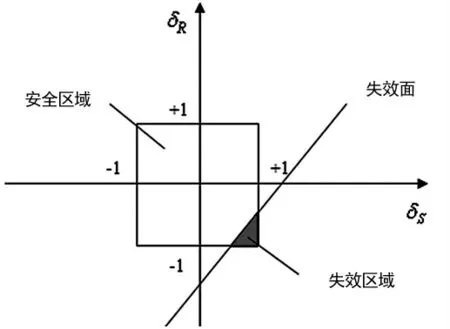
图1 应力-强度发生干涉的标准化空间示意图
标准化区间变量被分成2 部分,即失效域和安全域,将失效域面积与基本变量区域总面积之比定义为失效度,即
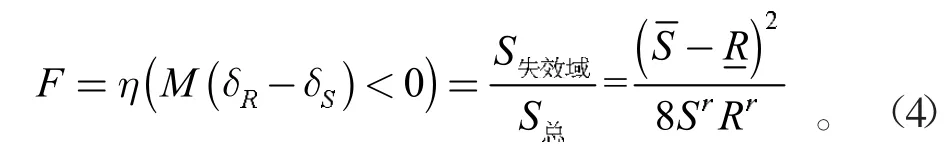
将安全域面积与基本变量区域总面积之比称为可靠度。即
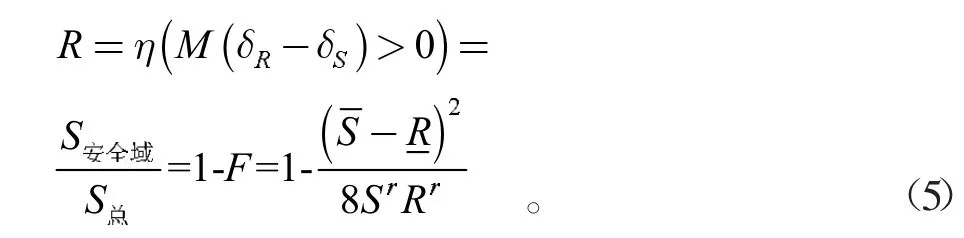
王晓军等[9]已证明该可靠性模型与概率可靠性模型的一致性。
1.2 随机-区间模型可靠度计算
当R 为随机变量,S 为区间变量时,由于工程中构件工作应力和材料强度在大多数时服从正态分布情况,取随机变量为正态变量。R~N(μ,σ2),应力区间为,可将随机变量R 转换为区间变量,其中(若按工程要求一般可取Rr=3σ)。

结构的失效概率为
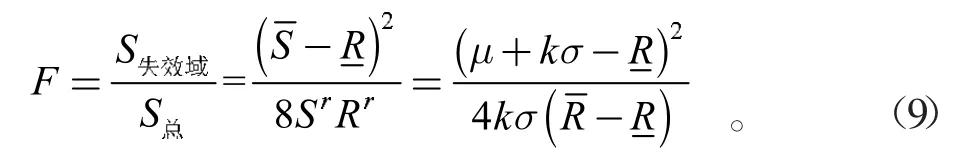
结构的可靠概率为
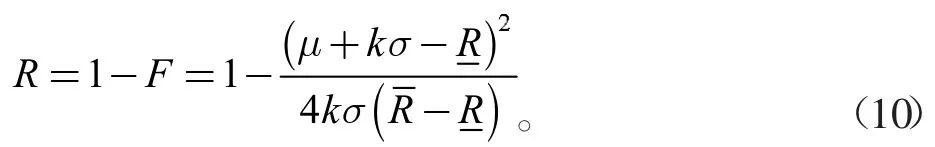
1.3 模糊-区间模型可靠度计算
当R 为模糊变量,S 为区间变量时,假设R 为L-R型模糊数所限定的模糊变量,其可能性分布函数为πR(r),对任一截集水平α,R 退化为区间变量[10],其上下界分别为

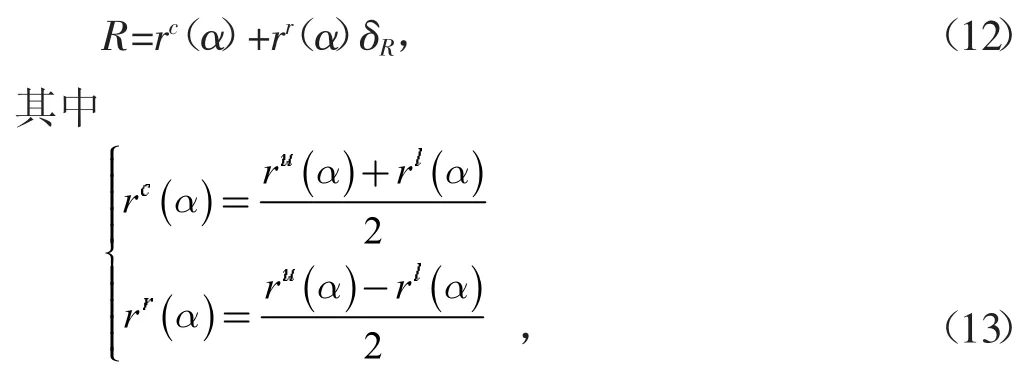
式(12)、式(13)中α∈[0,1]为单位区间变量,δR∈[-1,1]为标准化区间变量,从而有
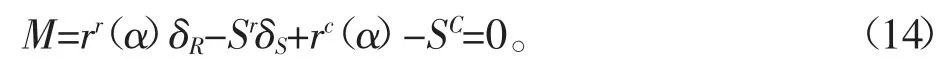
结构在截集水平α 下的失效概率为
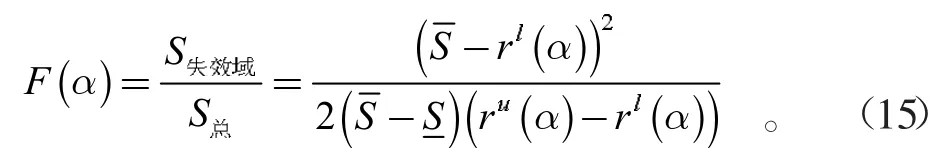
则结构的失效概率为对截集水平区间进行积分,即

以下仅说明结构在一定的水平截集α 下的失效或安全概率,结构的失效和安全概率可按照式(16)在截集水平区间进行积分计算。
结构在截集水平α 下的安全概率为
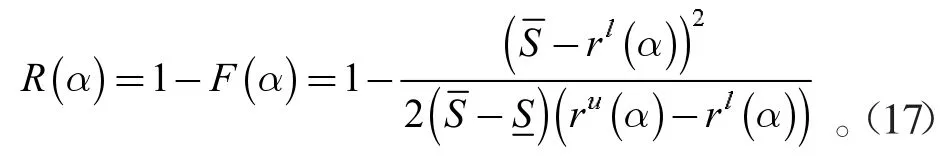
同理,当R 为区间变量RI=[R,R],S 为模糊变量时,设S 可靠性分布函数为πS(S),则S 可退化为区间变量S=S(Cα)+S(rα)δS。
则在截集水平α 下失效概率为
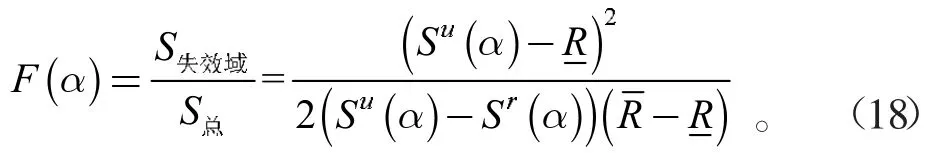
相应的在水平截集α 下可靠概率为
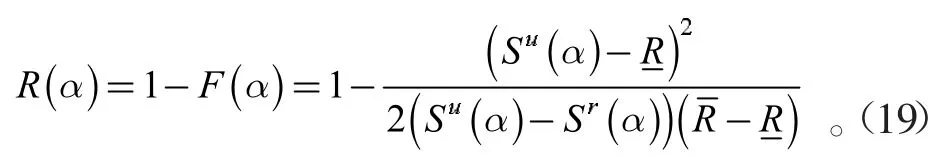
1.4 随机-模糊模型可靠度计算
当R 为随机变量,S 为模糊变量时,设R~N(μ,σ2),S 的可能性分布函数为πS(S),则R,S 分别退化为区间变量,其上下界分别为
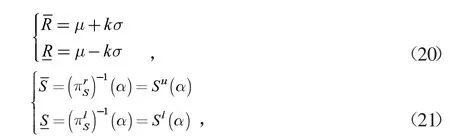

同理当R 为模糊变量,S 为随机变量时,R 可能性分布函数为πR(r),S~N(μ,σ2),R,S 分别转换为区间变量,得

1.5 模糊-模糊模型可靠度计算
当R,S 均为模糊变量时,其可能性分布函数分别为πR(r),πS(S),则对任一截集α,R,S 退化为区间变量,其上下界分别为[11]

2 数值算例
2.1 算例一
考虑如图2 所示悬臂梁,在固定端处为b1=2.0,b2=5.0 处分别作用2 个集中载荷P1和P2,取|mmax|≥mcr时结构发生失效,其中mcr为极限弯矩,mmax为梁中最大弯矩值,设基本区间变量为分别服从正态分布,P1~N1(5,0.22),P2~N2(2,0.12)。
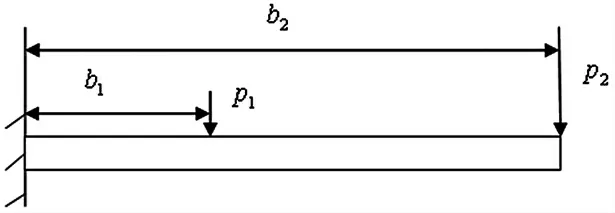
图2 悬臂梁结构示意图
建立结构功能函数
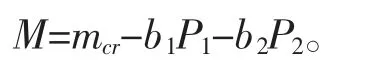
利用本文提出的随机-区间可靠度计算模型,可得

2.2 算例二
已知某结构的疲劳强度可靠性分布为如下三角形式
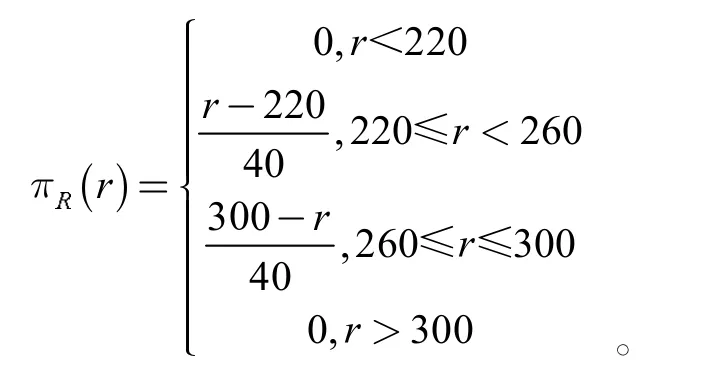
作用在结构上的随机应力服从正态分布S~N(180,21.62)。
取k=3,由本文提出的随机-模糊可靠度计算公式,可得表1。

表1 几种截集水平下可靠性分布
对截集水平区间积分可得结构的可靠概率为
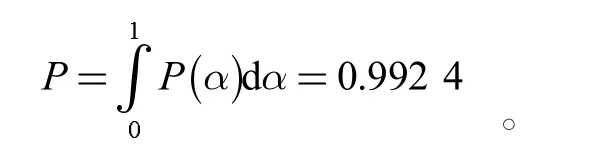
2.3 算例三
承受均布载荷的简支梁,其长度l=4 000 mm,截面宽度b=120 mm,截面高度h=240 mm,如图3 所示,载荷q 为随机变量并服从参数为μ1=217.6 和σ1=19.5 的正态分布,即q~N(μ1,σ21)N·mm-1,梁的材料为45 钢,其强度R 为模糊变量,其隶属函数分布为正态分布,即
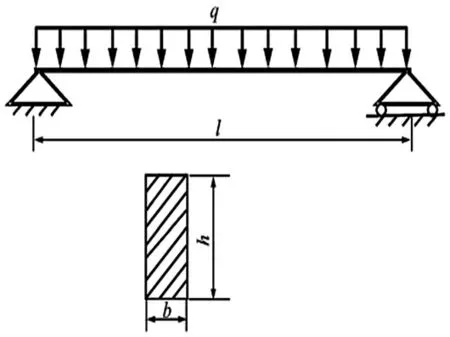
图3 简支梁受力图
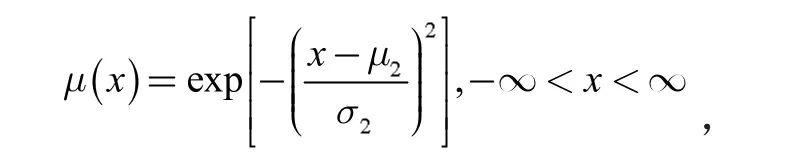
式中:μ2=463.5;σ2=35.5。计算结构的可靠度。
由材料力学可知,该简支梁最大应力为
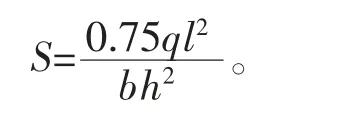
进而可求得应力S 的均值和方差分别为μS=377.7,σS=33.9。
取k=3,由本文提出的随机-模糊可靠度计算公式,可得可能性分布情况,见表2。
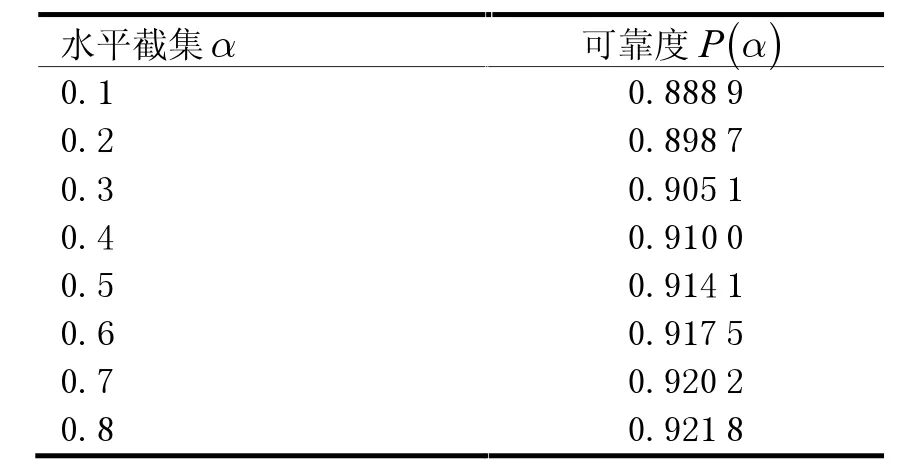
表2 几种截集水平下可靠性分布
对截集水平区间积分可得结构的可靠概率为
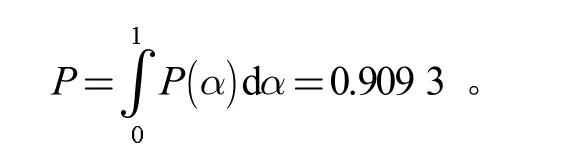
2.4 算例四
以典型的十杆桁架为例。如图4 所示。已知两跨跨长L=9.144 m,杆件材料的密度为ρ=2 768 kg·m-3,材料的弹性模量为区间变量,其分布区间为EI=[6.956 9e10,7.032 7e10]N·m-2,作用的载荷为区间变量,其分布区间分别为F1I=F2I=[400.32,489.28]kN,F3I=[1 601.28,1 957.12]。各杆的强度约束为[σi]=1.723 7e8 N·m-2,(i=1,2,…,8,10),[σ9]=5.171 1e8 N·m-2。节点2 处的铅垂方向的最大容许位移为模糊变量,其隶属函数分布为
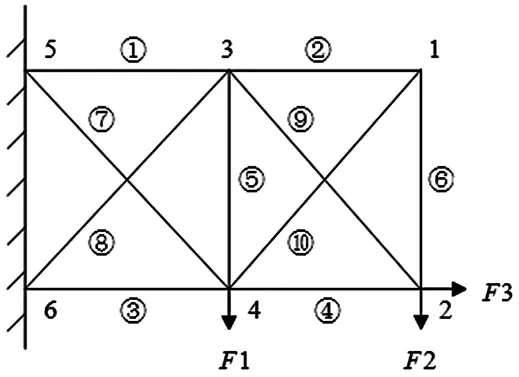
图4 十杆桁架结构
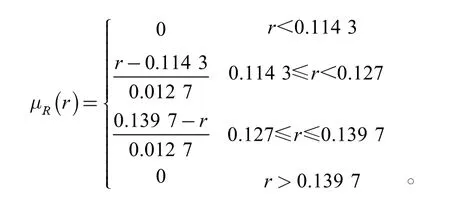
取各杆的截面面积为设计变量,各杆截面面积的下限取为6.4e-5 m2。进行该结构的截面优化设计。
此十杆桁架结构的区间-模糊可靠性优化设计模型为
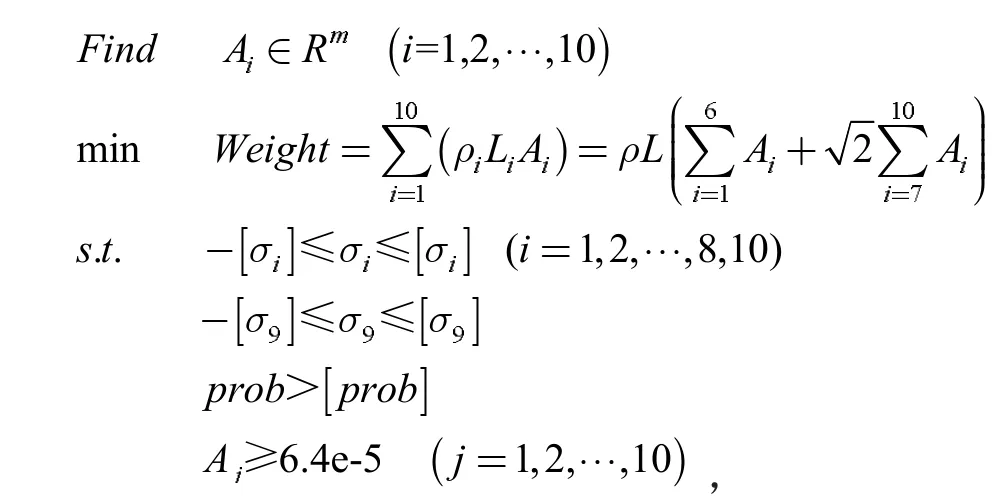
式中:prob 为节点2 处的位移约束对应的区间-模糊可靠度;[prob]为可靠度指标下限。确定性优化及考虑不确定因素的可靠性优化设计结果见表3。
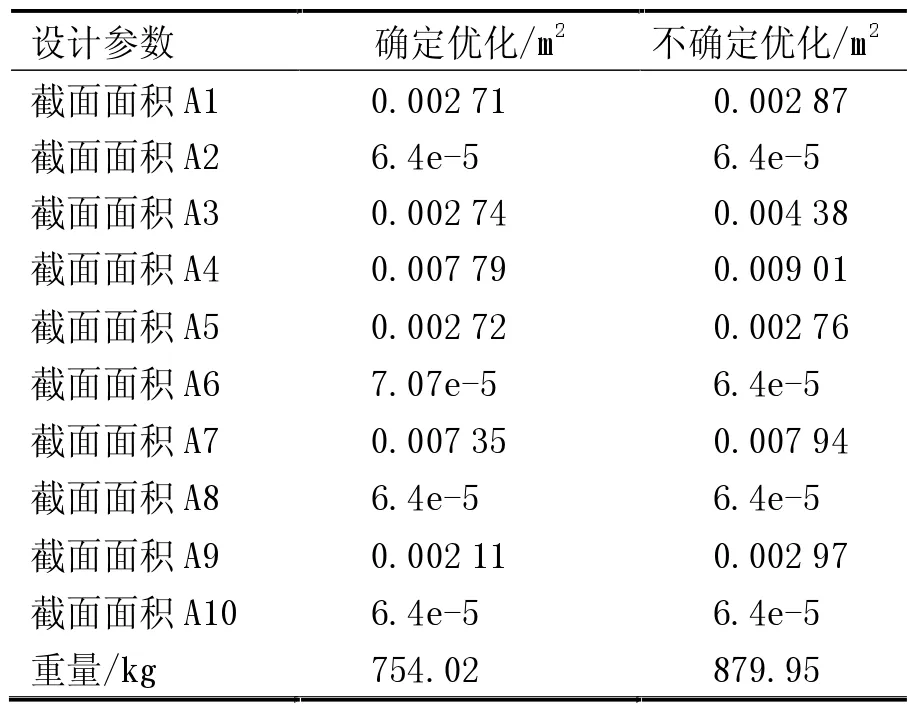
表3 优化设计结果
结论:当考虑不确定因素的影响时,不确定优化得到的重量比确定优化重量大,结果偏于保守。这正是考虑了材料及载荷的不确定性影响,在优化设计中加入了可靠性设计的结果,要获得更高的可靠性需要牺牲一定的目标函数值。说明实际工程中如果结构的目标函数可以适当放宽,应该适当考虑不确定因素对结构的影响,加入结构的可靠性设计,以提高结构的安全性。
3 结论
由于工程中存在大量随机模糊及未知然而有界等多种不确定信息,各种不确定信息的混合使得求解问题可靠性时不能单纯地利用随机概率可靠性和模糊可靠性方法求解。因此,有必要对混合不确定可靠性进行研究。文中基于体积比的非概率可靠性模型推导出的各种不确定组合的可靠度计算公式,可适用于相应的不确定工程问题,计算简便,意义明确,可作为混合不确定可靠性分析方法的一种补充。文中算例说明了本文方法的应用。
