标识密码学研究综述
2022-10-19石典佑
石典佑
(国防科技大学 计算机学院,长沙 410073)
随着信息技术的蓬勃发展,人们对信息安全愈发关注,而密码学则为信息的安全可靠提供了强有力的保障。根据通信双方是否使用相同的密钥,现代密码学可以大致分为对称密码学和非对称密码学2 大类。在对称密码学中,通信双方使用相同的密钥对消息进行加解密,运行效率高,且安全性不依赖于任何假设,因此具有统计学上的安全性。但是由于通信双方需要共享同一密钥,故其不可避免地需要解决对称密钥的分发问题。非对称密码通过设计2 种完全不同的密钥:私钥和公钥,避免了密钥分发带来的安全隐患。在加密方案中,加密方利用公钥对消息进行加密,而只有拥有对应私钥的解密方才能正确解密;而在签名方案中,签名方利用私钥进行签名,其他所有实体都可以利用公钥对签名的正确性进行验证。
然而在传统的公钥密码体制中,公钥的可靠性需要由可信的证书认证中心(Certificate Authority,CA)颁发数字证书作为安全凭证进行验证[1]。在大规模系统进行部署时,需要对海量的证书进行管理,频繁的证书交换与认证会降低系统的运行效率[2]。为避免数字证书颁发和验证引起的效率问题,Shamir[3]于1984 年首次提出了标识密码学(Identity-Based Cryptography,IBC)理念,将用户的邮箱、地址等身份标识直接作为用户公钥,无须数字证书即可确保公钥的可靠性,让密码方案更加轻便高效。
随着我国自主设计的商用标识密码SM9 成为行业标准,标识密码得到了更为广泛的应用,许多研究者更是进一步为标识密码引入更为丰富的功能与安全属性[4-6]。本文主要围绕标识密码学领域,结合当下的研究热点,对标识密码学的相关基础和研究现状进行梳理,最后对发展前景进行归纳总结。
1 预备知识
本章主要对标识密码学领域涉及的基本知识进行简要回顾,主要包括椭圆曲线、双线性对及其困难问题。
1.1 椭圆曲线
椭圆曲线(elliptic curve)在标识密码领域具有重要意义,椭圆曲线上的点群(the group of points of an elliptic curve)构成了标识密码基本的计算空间,其基本形式如图1 所示。

图1 椭圆曲线

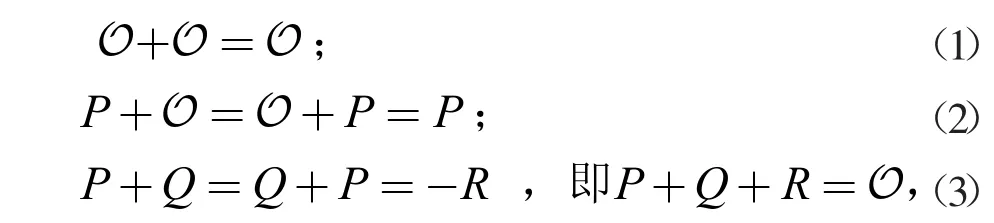
式中:-R 为R 的逆元,2 者关于x 轴对称;R 为P,Q 连线与的交点。
1.2 双线性对
双线性对(paring)是实现标识密码的重要工具,基于双线性对的困难问题是标识密码学安全性的基石。记G1,G2是q 阶加法群,Gr为q 阶乘法群,双线性对为满足如下条件的映射。
(1)双线性性(bilinearity):对于所有P∈G1,Q∈G2和成立。
1.3 双线性对上的困难问题
标识密码的安全性依赖于底层的困难问题假设,这些问题的困难性体现在不存在多项式时间算法能够对其进行求解。以下为常见的双线性对上的困难问题,其中,分别为q 阶循环群的生成元。

2 标识密码的算法定义
标识加密(Identity-Based Encryption,IBE)和标识签名(Identity-Based Signature,IBS)方案是标识密码学的2 个基本研究领域,其他诸如标识签密算法[5]、层次式标识密码[12]等密码原语则为其引入新的功能需求与安全定义。
2.1 标识加密方案
在传统公钥加密环境下,发送方需要从公开渠道获取接收方的公钥及数字证书对其进行验证。经过多次数据传输和计算验证后,发送方才能正式用该公钥向接收方发送第一条加密消息。在标识加密算法中,这一繁杂的过程将不复存在,发送方可以直接将接收方的标识(例如地址、邮箱等)作为公钥信息对数据进行加密发送给接收方。在标识加密算法中,存在一个可信任的密钥生成机构(Private Key Generator,PKG),接收方的私钥由PKG 进行计算。
标识加密方案IBE 包含以下4 个概率多项式时间算法:系统构建算法S,密钥生成算法G,加密算法E和解密算法D。
系统构建算法S(λ)由PKG 运行,输入安全参数λ,输出系统主公私钥对(mak,msk)。
密钥生成算法G(msk,id)由PKG 运行,输入主公钥mpk 和用户身份标识id,输出用户私钥skid。
加密算法E(mpk,id,m)由加密方运行,输入主公钥mpk、接收方身份标识id 和明文m,输出密文c。
解密算法D(skid,c)由解密方运行,输入用户私钥skid和密文c,输出明文m(若密文不正确,则返回一个特殊值⊥)。
对于标识加密算法而言,其正确性表现为对于同一个主公私钥对,正确加密的密文总能被对应的接收方正确解密,即

式中:ID 为有限标识空间;M 为有限消息空间;C 为有限密文空间。
2.2 标识签名方案
标识加密算法保护数据的机密性,标识签名算法关注的是数据的完整性。标识签名算法利用私钥对消息进行签名,数据的接收方可以利用发送方的标识对签名和消息的一致性进行验证,一旦消息遭到篡改,接收方可以通过签名及时发现。同时,由于只有拥有私钥的一方才可以生成可以利用标识进行验证的合法签名,因此也实现了消息发送方的不可抵赖性。
标识签名方案IBS 由以下4 个概率多项式时间算法构成:系统构建算法S,密钥生成算法G,签名算法I和验签算法V。
系统构建算法S(λ)为PKG 运行的概率性算法,输入安全参数λ,输出系统主公私钥对(mak,msk)。
密钥生成算法G(msk,id)为PKG 运行的概率性算法,输入主公钥mpk 和用户身份标识id,输出用户私钥skid。
签名算法I(skid,m)为签名方运行的概率性算法,输入私钥skid和消息m,输出签名σ。
验签算法V(mpk,id,m,σ)为验签方运行的确定性算法,输入主公钥mpk、签名方的标识id 和签名σ,输出accept 或reject。
标识签名算法的正确性表现为在相同的主公私钥对(mak,msk)下,签名方运行算法I 得到的签名σ 总能被以其标识id 为输入的算法V 所接受,即

式中:ID 为有限标识空间;M 为限消息空间;Σ 为有限签名空间。
3 标识密码学的研究现状
自Shamir[3]于1984 年首次提出标识密码学以来,标识密码学领域的相关研究工作已经愈发完善。标识密码学的研究范围在不断扩展,标识签密、层次式标识密码等不同概念的相继提出,满足了不同的应用场景与安全需求。就在2020 年,我国自主设计的SM9 标识系列密码成为了我国国家标准,围绕SM9 的应用拓展和安全分析进一步成为了当前学术界的研究热点。本章分别从标识密码的相关研究和国密SM9 的相关研究2 个方面来阐述标识密码学的研究现状。
3.1 标识密码的相关研究
1984 年,Shamir[3]首次提出了标识密码的概念,用户可以直接利用邮箱、地址等字符串作为用户标识,用于加密和签名的操作,消除了传统公钥密码体系对数字证书的依赖,标识密码自此受到学术界的广泛关注。但是,直到2000 年,尽管许多学者针对标识密码的理念提出了不同的方案构造,却均缺乏实用性。直到2001年,Dan 等[7]利用双线性对,成功构造出了第一个具有实用价值的标识加密方案。于是,双线性对被广泛应用于标识密码的构造中,许多高效的方案被相继提出。
标识密码算法需要一个密钥生成机构(Private Key Generator,PKG)负责所有节点的私钥生成,在大规模的系统部署中,PKG 需要承担高额的计算和通信开销。为缓解单一PKG 的压力,Jeremy 等[13]提出了层次式标识加密(Hierarchical Identity-Based Encryption,HIBE)的概念,将系统节点部署为树形结构,各级PKG均有为其子节点生成密钥的能力,从而缓解了单一PKG 进行密钥分发的负担。同年,Craig 等[14]设计了首个层次式标识签名算法(Hierarchical Identity-Based Encryption,HIBS),但是没有给出具体的安全分析。在2005 年,Sherman 等[15]在随机预言机模型下提出了第一个可证明安全的HIBS 方案。Li 等[16]在2006 年提出了标准模型可证明安全的HIBE 方案,同时文章也给出了一个HIBS 的新构造,具有比Sherman 等[15]的方案更高的运行效率。在上述的HIBE 和HIBS 方案中,节点的密钥长度和签名长度随着节点的深度而不断增长,在大规模的系统部署时,位于底层的节点运行时需要使用更多的计算资源与传输带宽。
为解决层次式标识密码计算通信开销随节点深度增长而增加的问题,DAN 等[17]提出了密文定长的HIBE算法。同年,Yu 等[18]在密钥生成阶段,增加了各层参数的运算过程,从而避免了公钥参数随节点层级增加的问题。2013 年,Wu 等[19]进一步对算法进行了改进,提出了具有更短密钥的HIBS 方案。
在安全性方面,标识密码的前向安全属性也是学者广泛研究的一个热点问题。传统的加密和签名方案中,一旦私钥遭到泄露,那么敌手可以解密过去任意时间点的密文,伪造过去任意时间点的签名。满足前向安全性的方案可以保证即使某一时刻的密钥遭到泄露,过去时间产生的密文和签名依然能够保证安全。2008年,Liu 等[20]基于双线性对,提出了首个前向安全的标识签名算法(Forward-Secure IBS,FSIBS)。不过遗憾的是,文章仅对方案的安全性进行简要的分析,未给出形式化的安全证明。Yu 等[21]在给出了FSIBS 正式的算法定义和安全模型后,给出了第一个具有可证明安全的FSIBS 方案。Hyunok 等[22]和Hankyung 等[23]分别提出了主密钥泄露情况下的FSIBS 方案。Wei 等[24]进一步考虑到标识密码算法中可撤销的安全属性,利用二叉树对所有节点进行管理,实现了可撤销的FSIBS 方案。
3.2 国密SM9 的相关研究
SM9 是我国自主研发的标识密码算法,具体包括数字签名算法、密钥交换算法、密钥封装机制和公钥加密算法,具有可证明的安全性[25]。如今不但成为了我国国家标准,而且也纳入了国际标准之中[1],在物联网安全[26]、智能变电站安全防护[27]、区块链隐私保护[28]和移动互联网身份认证[29]等领域均取得了广泛的应用。
甘植旺等[30]考虑到SM9 密码体制运行效率问题,通过对SM9 中重要的R-ate 双线性对进行分析,提出了一种快速计算的算法,显著提升了算法的运行效率。王明东等[31]进一步针对R-ate 双线性对中模幂运算进行优化,与传统实现方式相比,性能提高近3 倍。王松等[32]通过参数预计算的方式,提高了SM9 签名和验签的速度,同时对指数和乘法运算进行优化,提高了SM9签名验签算法的运算性能。杨国强等[33]将基于固定基的快速模幂算法应用于SM9 的FPGA 实现中,将SM9签名算法提升2.3 倍。
基于SM9 标识系列密码,学者们提出了各种扩展方案。张超等[4]利用SM9 标识加密算法,设计了具有可证明安全的可搜索加密方案,将安全性归约到DBDH问题的困难性假设上。赖建昌等[5]对SM9 标识加密算法进行改进,提出了加密与签名相结合的标识签名算法,并通过严格的安全证明,将方案的安全性归约到了底层q-SDH 和q-BDHI 问题的困难性假设上。盲签名是数字签名领域的一种重要技术,其允许签名者在对消息未知的情况下进行签名,张雪锋等[34]基于SM9 标识签名算法提出了具有比传统RSA 机制下更高效率的盲签名方案。另外,张雪锋等[35]进一步设计了基于SM9 的环签名方案。但是他们的方案仅给出了简单的安全说明,并未给出严格的安全分析。彭聪等[36]在随机预言机模型下,给出了可证明安全的基于SM9 的环签名方案,与相关工作相比,方案在签名和验签效率上均有提升。安涛等[37]基于SM9 标识密码算法提出了聚合签名方案,大大提升了认证效率。
4 标识密码学的发展前景
综合考虑学术界标识密码学的现有研究成果,未来对标识密码学的研究可以主要集中于以下3 个方面。
4.1 效率
现有的标识密码算法广泛使用椭圆曲线上的双线性对进行构造,因此如何加速双线性对的运算速度是提升算法整体运行效率的关键。此外,根据所选择的椭圆曲线不同,对算法的实现也有不同程度的影响。因此,未来可以考虑从底层算法优化的角度出发,考虑寻找、选取更合适的配对友好椭圆曲线,优化椭圆曲线点群中加法的运算效率,结合双线性对的结构特点,降低其计算开销。此外,可以进一步结合硬件实现,设计双线性对的硬件电路,从底层实现双线性对运算的加速优化。在另一方面,可以进一步寻找合适的数据结构,在标识密码算法的设计中,降低椭圆曲线点群和双线性对的运算次数,减少生成与传输的参数规模,从而提高标识密码算法的计算和通信效率。此外,可以进一步结合云计算,将椭圆曲线点群和双线对的运算,以及其他诸如大整数模幂等需要占用大量计算和存储资源的操作外包给云服务器,从而降低单个节点的运算负担。
4.2 安全性
层次式标识密码算法的提出,将传统标识密码中单个PKG 的负载逐级下放,减轻单个PKG 的密钥分发负担。但是各级PKG 为下层节点分发的私钥使用的是其自主产生的随机数,此随机数的来源无法认证,子节点无法对得到的私钥进行验证,可能存在中间人攻击的风险。因此,可以为私钥的产生提供进一步的验证机制,将私钥和PKG 的标识进行绑定,使子节点可以通过公开参数对私钥来源进行验证。在标识密码学的前向安全性上,目前学术界广泛采用的实现方式是基于二叉树或基于强RSA 难题假设[38-39]。基于二叉树的方案节点需要保存大量的私钥用于实现节点的密钥自更新,而基于强RSA 难题假设的方案涉及大量的模幂运算。因此,可以考虑寻找新的工具对标识密码学的前向安全性进行实现,提升其运行效率。此外,当量子计算机来临时,公钥密码学的基本难题假设大整数分解和离散对数问题将不再困难,对标识密码学的经典算法会造成严重威胁。因此,设计后量子安全的标识密码算法也是当前的一个研究热点。
4.3 应用
标识密码学在电子邮箱等网络通信领域可以降低通信轮次,提升通信效率;在物联网系统中,可以避免数字证书的引入,减小物联网节点的资源占用。未来在隐私保护领域,可以考虑进一步实现标识的匿名化,即考虑加密方和签名方在通信过程中保持标识的隐蔽性,防止敌手通过密文或签名对消息的来源进行溯源。在同态加密领域,可以考虑具有同态操作的标识加密算法或标识签名算法,使得加密方或签名方直接在密文或签名上进行数据的添加,减少频繁加密和签名带来的开销。对于其他密码原语,诸如盲签名、环签名和阈值签名,可以进一步考虑使用国密SM9 标识密码算法进行实现,进一步丰富国产密钥的应用场景,设计更多自主可控的密码方案。
5 结束语
本文围绕标识密码的相关背景、算法定义和研究现状对标识密码的研究进展进行了较为详细的总结与回顾。标识密码学经过将近40 年的不断丰富完善,成为了备受关注的研究热点。标识密码不但可以消除对传统数字证书的依赖,而且还可以进一步构造更具实用性和安全性的算法协议。未来在针对新的应用场景和后量子领域,可以通过引入新的功能需求和安全属性,从而进一步完善标识密码的相关研究。国密SM9 作为我国自主研发的标识密码算法,具有安全、灵活和易拓展等特点,对SM9 标识密码算法展开研究,既可以提出安全高效的算法协议,还可以加强国家安全领域的自主可控,无论是在理论方面还是实践方面均有重大意义。
