水下无人航行器空间运动建模与操纵性仿真预报

常开应，王庆云，沈鹏，臧斌

(1.昆明海威机电技术研究所(有限公司)，云南 昆明 650217；2.国家深海基地管理中心，山东 青岛 266237)

0 引 言

水下无人航行器（UUV）是海洋资源开发、海洋环境监测及海洋生态保护等的关键装备之一。近年来，随着人类对深海资源开发的不断深入，UUV 由于在军事与科研方面有重要应用，引起了广泛关注，研究价值和意义也日益凸显。

操纵性能是UUV 总体性能的主要指标之一，直接影响着航行器执行作业任务的能力，在航行器初步设计和运动控制参数选取时，操纵性能的预报尤为重要。建立合理的空间运动数学模型是研究UUV 操纵性及控制系统设计的基础，王波、赵金鑫等参考潜艇操纵性研究的方法搭建了非线性的UUV 空间运动数学模型进行了仿真预报，段斐等针对REMUS 模型中的推力（力矩）和舵力（力矩）难于获取等问题，提出了一种修正的REMUS 模型并完成了航行器的运动仿真预报。戴君锐等采用六自由度模型完成了UUV操纵运动仿真，并与K-T 模型的仿真结果进行了对比。徐得志等参考舰船操纵性理论研究方法，采用四阶龙格-库塔算法对UUV 垂向操纵运动进行了研究。聂为彪等建立了UUV 水平面内的动力学方程，应用Matlab 编程对研究对象的水平面操纵运动进行了预报。

本文基于水下航行力学基本原理，参考鱼雷操纵性基本理论，在小冲角、小侧滑角、小机动运动条件下导出了UUV 六自由度空间运动的线性数学模型，并搭建了操纵运动仿真预报平台，对某型UUV 单平面典型操纵运动特性进行仿真预报，为UUV 水动力布局和控制系统的设计提供一定的技术指导与理论支撑。

1 UUV 空间运动数学模型

1.1 基本假设

1）UUV 是刚体，并关于 平面对称；

2）流体是无粘不可压缩的；

3）流体为无界流场，在航行体运动之前是静止的；

4）坐标原点与UUV 浮心重合；

5）不考虑地球的自转和地球的曲率，近似认为地面坐标系为惯性坐标系。

1.2 坐标系选择与运动学参数

采用如图1 所示坐标系，包括地面坐标系EXYZ和航行体坐标系。地面坐标系与大地相连，航行体坐标系与UUV 相连，坐标原点与UUV 浮心重合。

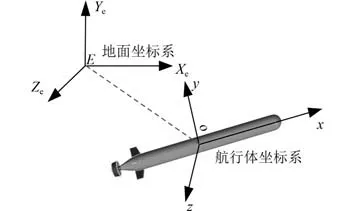
图1 水下无人航行器坐标系Fig.1 Coordinate system of underwater unmanned vehicle

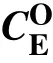
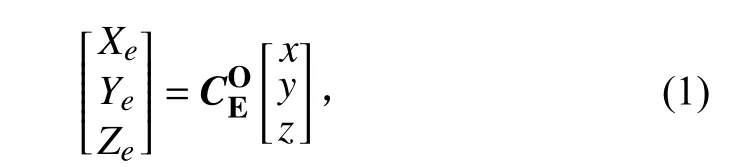
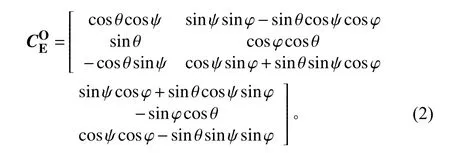
运动参数包括：

1）UUV 在地面坐标系中的位置（X,Y,Z）和姿态角（φ，ψ，θ）；

2）航行体坐标系下的UUV 速度（v,v,v）和角速度（ω,ω,ω）；

3）UUV 速度和速度的流体动力角 α，β关系如下式：

1.3 运动学方程

根据UUV 速度在地面坐标系和航行体坐标系下的转换关系，可得平动运动学方程：

由UUV 旋转角在地面坐标系和航行体坐标系下的关系，可得转动运动学方程：

1.4 动力学方程

根据动量定理和动量矩定理，可以得到UUV 在无流界中的动力学运动方程，并通过系列的推导，可表示为矩阵形式：

式中：

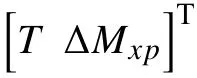
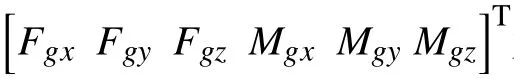
2 UUV 操纵运动仿真平台搭建

搭建操纵性仿真预报平台，该平台将航行体空间运动数学模型分为姿态角模型、速度转化模型、粘性流体动力模型、静水力模型、其他力模型、坐标系转换模型等。

仿真预报过程中采用变步长四阶-五阶Runge-Kutta 算法，输入UUV 基本参数及水动力参数，并赋予初始速度、推力和舵角，运行程序后便可输出对应时刻UUV 的姿态角、位置、速度等，生成对应曲线图，即可对UUV 的操纵性能进行预报。

表1 UUV 总体参数Tab.1 The parameters of underwater unmanned vehicle

3 UUV 操纵运动仿真预报

3.1 水平面运动仿真

3.1.1 回转运动预报

给定推力值＝95.96 N，对应设计航速4 kn，初始速度=2 m/s，并分别操垂直舵 δ=10°，15°，20°，其浮心的运动轨迹详如图2 所示，结果如表2 所示。

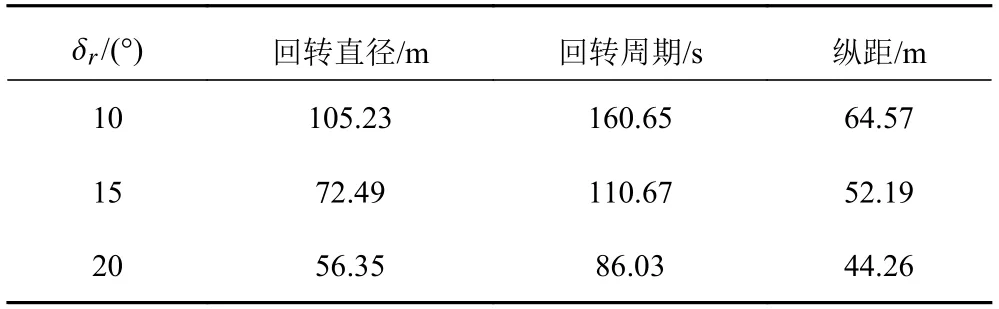
表2 UUV 回转运动特征参数Tab.2 Rotary motion characteristic parameters of underwater unmanned vehicle

图2 航速4 kn 时，不同舵角的回转曲线Fig.2 Rotation curve of different rudder angles at 4 kn

可以看出，在设计航速为4 kn 下，舵角越大，回转直径、回转周期和纵距越小。在操大舵角20°时，回转直径为56.3 m，约为航行体长（7 m）的8 倍，可以看出该UUV 具有较高的水平面回转性能。

3.1.2 水平面Z 形操舵预报

给定推力值，初始速度，对应航速分别为4 kn和8 kn 下，对于 δ/ψ=15/15进行Z 型操舵运动，反复操舵4 次，其偏航角 ψ 和舵角 δ随时间的变化轨迹如图3 所示。由此得到UUV 的初转期t、超越时间、超越偏航角 ψ、全周期T等特征参数，便可评估UUV 水平面航向改变性能。

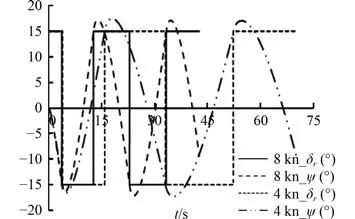
图3 不同航速下，偏航角 ψ 和舵角 δr随时间的变化曲线Fig.3 Curves of yaw angle ψand rudder angle δr with the change of time at different speeds

从表3 可以看出，航速8 kn 时，UUV 的初转期t、超越时间、超越偏航角 ψ、全周期T均比低航速4 kn 时小。此外，还可以看出，该UUV 具备良好的应舵性和操纵性，响应时间快。

表3 UUV Z 形操舵运动特征参数Tab.3 Z-shape motion characteristic parameters of underwater unmanned vehicle

3.2 垂直面运动仿真

3.2.1 垂直面T 形操舵预报

给定推力值，初始速度，对应航速分别为4 kn和8 kn 下，操升降舵 δ=15，UUV 的俯仰角 θ和深度Y等都在改变，当俯仰角达到设定俯仰角10°时，立即回舵到初始状态，当俯仰角速度为0 时，θ达到稳定值，UUV 稳定在一个新的航向上。升降舵 δ、俯仰角θ、航行深度Y随时间的变化轨迹如图4 所示。

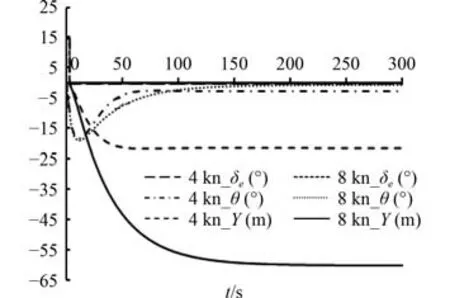
图4 不同航速下，升降舵 δe、俯仰角 θ、航行深度Ye随时间的变化曲线Fig.4 Curves of elevator δe、pitchθ and depth Y e with the change of time at diff erent speeds

从表4 两个响应航速结果可以看出，航速越大，UUV 的初转期t越小，说明UUV 的应舵更快，转首性好，下潜快，但同时超越俯仰角 θ和越深度 ξ也越大。此外，从图4 可以看出，航速越大，航行器稳定在新的航向上的时间也越长。

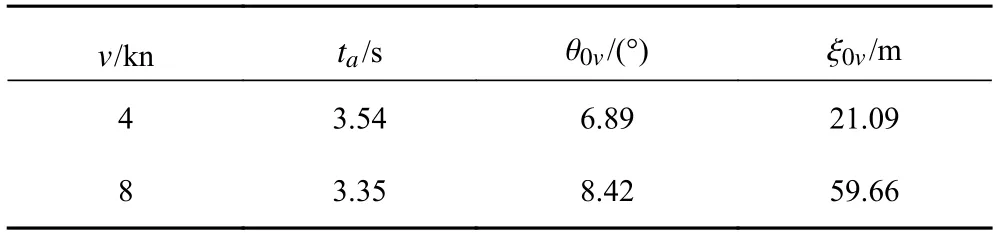
表4 UUV T 形操舵运动特征参数Tab.4 T-shape motion characteristic parameters of underwater unmanned vehicle

3.2.2 垂直面纯下潜预报

给定推力值T，初始速度，在设计航速4 kn 下，分别操横舵 δ＝ 15°，10°进行下潜，其俯仰角 θ和深度Y随时间的变化轨迹如图5 所示。

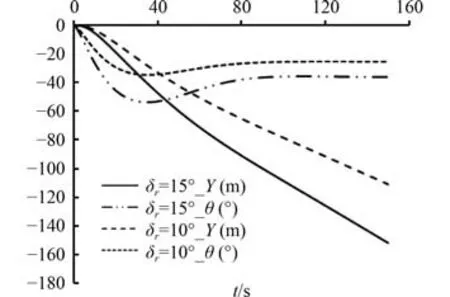
图5 航速4 kn 时，俯仰角 θ、航行深度 Ye 随时间的变化曲线Fig.5 Curves of pitchθ and depth Y e with the change of time at 4 kn

从图5 可以看出，在同一航速为4 kn 下，操横舵角越大，UUV 转首性越好，下潜得也越快，但对应稳定后的俯仰角也越大，符合UUV 的实际操纵运动特性。

4 结 语

本文基于水下航行力学基本原理，参考鱼雷操纵性基本理论，导出了UUV 六自由度空间运动线性数学模型，并搭建了操纵运动仿真预报平台，采用变步长四阶-五阶龙格-库塔（Runge-Kutta）算法，对某型UUV 的水平面回转、Z 形操舵运动以及垂直面T 形操舵、纯下潜等运动进行了仿真预报。仿真结果表明，该UUV 具备良好的应舵性和操纵性能，响应时间较快，能真实地反映研究对象的操纵运动特性，其结果可为UUV 水动力布局和控制系统的设计提供一定的技术指导与理论支撑。