基于博弈论的城市道路空间路权分配研究
2022-10-18杨国旭丁立民
杨国旭, 丁立民
(中国人民公安大学交通管理学院, 北京 100038)
0 引言
随着我国经济发展和城市化进程的加速,机动车保有量持续上升,城市交通拥堵问题也日益突出[1]。 近年来,虽然各地大力发展公共交通并取得一定成效,但总体而言,公交出行对非公交机动车出行的吸引力仍然不足,交通拥堵也未得到根本缓解。十四五规划要求加快绿色、环保、高效、低碳经济的发展,进一步促进交通的绿色升级,十九大也明确提出要建设交通强国,快速推动绿色、低碳、安全、高效系统化交通体系的搭建[2]。 推动绿色交通发展,缓解道路交通拥堵,除了科学调控机动车保有量、不断降低私家车使用强度外,更应当重视基于道路资源分配公平正义的交通系统可持续发展。
针对道路空间路权问题国内外学者都进行了一定研究。 国内有学者从路权分配概念入手,研究出行者路权分配的法律保障问题,利用法律规制改善路权分配现状;还有学者运用运筹学、排队论构建路网模型,仿真模拟公交专用道的设置,提出公交专用道的设置条件及具体方案[3-8]。 国外并没有“路权”这一独立概念,因此对路权的研究也相对较少,主要从公平和效率角度对道路使用情况进行研究,通过模拟技术分析设置公交专用道的效益,提出城市优先发展公共交通的策略[9-12]。 纵观国内外现有文献,鲜有涉及对机动车道内公交及非公交机动车空间路权分配的研究。
近年来,博弈论在国内外交通领域得到了广泛应用,包括驾驶人的路径选择、城市的交通组织管理等,但较少应用于道路空间路权的分配[13-14]。 道路空间路权的分配,其实质是对道路空间资源的分配,体现了不同交通方式之间的利益博弈。 本文选择博弈论作为研究方法,以城市干路的机动车道作为研究对象,对公交车与非公交机动车之间的路权分配进行研究,从而进一步优化交通出行结构,为探索解决城市交通问题新机制提供理论依据,实现空间资源分配的公平正义。
1 基于博弈论的空间路权分配模型
1.1 博弈参与人
本文对机动车外的其他出行方式不作考虑,将机动车分为公交车和非公交机动车两类。 由于机动车车道的数量是由交通管理者确定的,所以该博弈共涉及3 方参与者,即:公交出行者、非公交机动车出行者和交通管理者。
1.2 影响出行方式选择的因素
为确定影响出行者出行方式选择的因素,本文设计并发放了1 800 份调研问卷,收回有效问卷1 715 份,调查结果如表1 和图1 所示。

表1 影响出行方式选择的因素问卷调查结果
表1 表明,影响出行者出行方式选择的因素排在前3 位的依次为出行时间、出行费用成本与出行舒适度。
图1 表明,在选择出行方式时,出行费用对于高收入人群的影响较小;随着人均年收入的提高,出行者对于出行私密性和舒适性的要求越来越高,即非公交出行方式的吸引力越来越强;出行时间对于高收入和低收入人群的影响相对较小。

图1 人均年收入与出行方式选择因素的关系
1.3 模型假设
为了建模需要,做如下假设:
(1)车辆密度只与出行时间有关;
(2)交通流量总体保持相对恒定;
(3)机动车道宽度与条数保持恒定;
(4)出行方式的选择只与出行时间、费用成本及舒适度有关;
(5)博弈3 方都是理性的,出行者能够全面了解交通信息,不会出现信息的非均衡性。
1.4 双层规划模型构建
交通管理者能够决定两种车道(公交专用道和非公交机动车道)数量的多少,并根据交通状况对两种车道数量进行调配,出行者则会依据车道调配情况选择合适的出行方式。 基于此,构建空间路权分配双层规划模型。
1.4.1 目标函数
上层为:
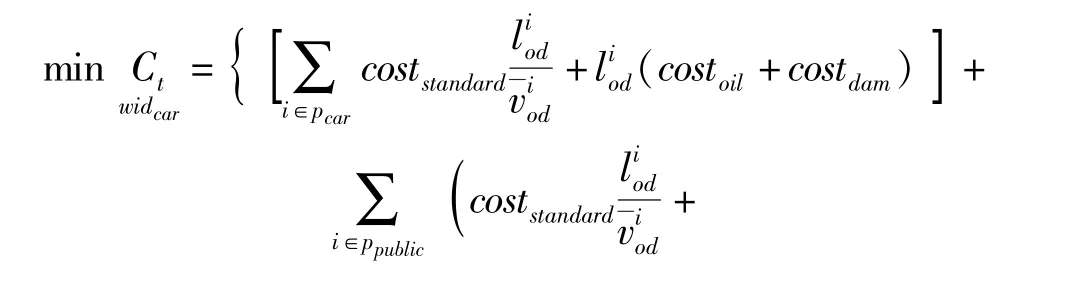

需要说明的是:管理者通过调配公交车道和非公交机动车道的数量来均衡二者出行之间的利益,实现其出行时间和出行费用成本最小化,满足出行舒适度,从而达到系统最优。 由于出行者是以出行成本作为选择出行方式的依据,因此,下层目标函数以出行人数作为优化变量,把出行时间和非舒适度转换成出行费用,将个人的出行费用定义为广义出行费用。
1.4.2 约束条件
(1)出行人数约束
基于假设,当两类车道数量发生变化时,两种出行方式的出行分担率会发生变化,但是出行人数总量保持不变,如式(3)所示。 同时,出行者对出行方式的选择符合式(4)约束要求。

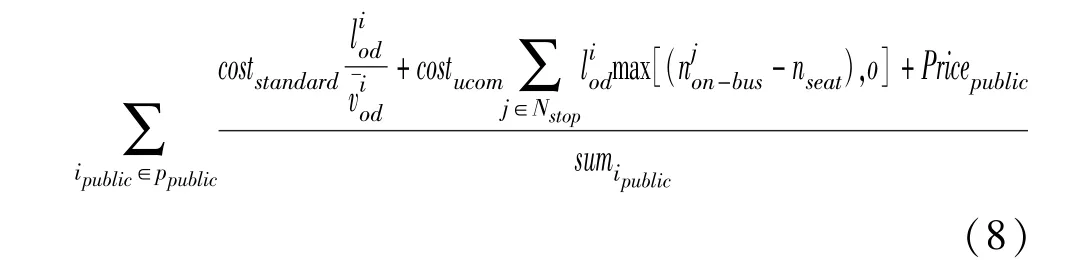
其中:icar、ipublic分别表示非公交机动车和公交出行人数。
2 双层规划模型求解
2.1 方法及流程
在构建的双层规划模型中,上层规划模型是整个系统出行最优模型,下层规划模型是出行者出行方式选择模型。 上层规划模型解决的是车道数量的分配问题,但是现实中不同车道数量类型较少(双向4 车道到双向16 车道共计7 类),结合文献分析[15],当单向公交专用道小于等于两条时,车道数量划分解域很少,因此,上层规划模型选用枚举法进行求解。 由于两种出行方式人均出行费用会随二者车道数量分配的变化而变化,因此,下层规划模型的目标是通过车道数量的分配使两种出行方式的人均出行费用达到动态平衡。 由于该问题属于非线性规划范畴,故下层规划模型选用混沌优化算法进行求解。
具体求解流程如图2、图3 所示。
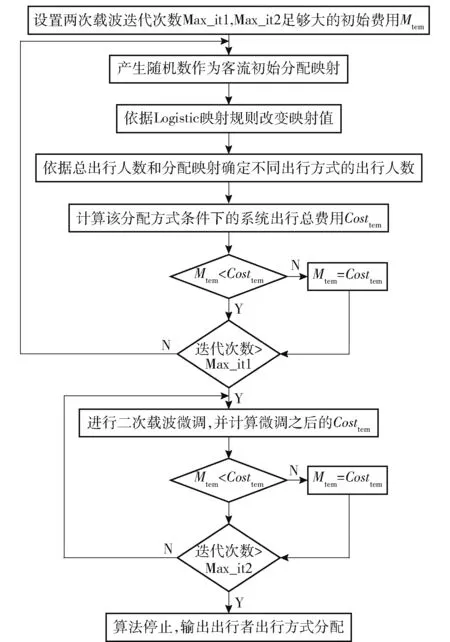
图3 出行者出行方式分配求解流程图
2.2 求解过程
求解过程包括以下四个步骤:
步骤1:设置临时变量,Mtem为初始广义费用,且足够大,主要对临时的目标函数进行存储。
步骤2:将公交专用道的条数Bus_lane设定为1,非公交专用道条数Car_lane为车道总数T_lane-1。
步骤3:确定车道条数分配策略。 通过平衡各种交通方式的广义费用来对不同出行者设定相应的出行方案,用混沌算法进行两次载波优化,以此获得出行者数量的分配方案,分别用Max_it1 和Max_it2代表两次不同的载波迭代次数峰值,载波过程如下:
第一次载波:
(1)形成两个随机数,分别为rand_num1、rand_num2,这两个随机数的作用是对人数进行分配映射。
(2)计算两种出行方式的出行者数量。 两种出行方式出行者总量为total_num,非公交机动车出行者数量为car_num,其计算公式为:

(3)计算该分配方式的总体出行费用Costtem,若Costtem小于Mtem,则将Mtem设置为Costtem,并对该分配方式进行记载。
(4)根据载波更新方式对出行者分配映射方法进行选取。 本文选择了经典更新方式,如式(11)所示。 为防止映射过程出现局部收敛,对经典更新方式进行了优化,即通过u值(随机设置为2、4、6、8)的变化扩大整体收缩范围。 判断首次载波迭代次数是否达到预期峰值,若达到则转入下一步骤,若未达到则转入步骤2。
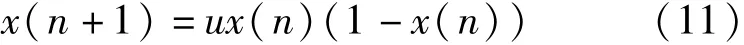
首次载波结束后,虽然接近了优化目标,但是预期结果还没有完全实现,所以要进行第二次载波。
第二次载波:

(2)由于映射信息发生变化,需重新计算该分配方式的总体出行费用Costtem,若Costtem小于Mtem,则将Mtem设置为Costtem,并对该分配方式进行记载。
(3)判断第二次载波迭代次数是否超过设定的载波峰值Max_it2,若超过峰值,则转入下一步,未超过则返回至第二次载波(1)。
步骤4:判断公交专用道的条数。 若公交专用道数小于等于1,则在原基础上增加1,相应地,非公交机动车道减少1,并返回至步骤3;若公交专用道数大于1,则确定车道数量分配方案以及出行者出行方式分配方案。
3 实例验证
3.1 路段选取
为验证本文所提出的模型和算法,本文选取了郑州市紫荆山路(紫荆山路与陇海快速路交叉口到紫荆山立交路口)2.7 km(如图4 所示)作为研究验证路段,该路段为双向八车道且上下行方向各设有一条公交专用道,有5 条公交路线(269 路、29 路、62路、86 路、Y16 路),交通流量较大,早晚高峰时段易发生交通拥堵。

图4 紫荆山路研究验证路段位置图
3.2 误差检验
要确定车辆运行速度与车道宽度以及小时流量之间的关系,需要调查不同车道分配方式下的车辆平均速度。 然而,由于条件限制无法获取该平均速度,为了便于分析,拟采用VISSIM 软件进行仿真,过程如下。
首先,将车道宽度设定为3.5 m,同时在VISSIM仿真软件平台中设计4 种不同的车道分配方式;其次,设定交通流量最小值为10 veh/h,最大值为8 000 veh/h,将其导入至VISSIM 仿真软件中不同车道分配方式的相应路段内,得到不同车道分配方式下的车辆平均速度;最后,运用Matlab 神经网络工具进行拟合。 训练过程如图5 所示。

图5 误差训练迭代图
图5 表明,经过约500 次的神经网络训练迭代,误差率呈现出收敛特性,最终经过636 次迭代,误差率稳定在11.48%。
3.3 求解及分析
3.3.1 参数设置
模型参数设置为:每条线路公交高峰小时流量为50 veh/h,公交车的平均座位数为26 个,公交车最高载客量为80 人,公交专用道最多为2 条,公交车票价为1.5 元/人;非公交机动车载客量均值为2人,油耗为0.8 元/km、车辆折损费为0.5 元/km,人均时间成本为30 元/h,舒适性的折减量为0.2 元/人/km[16]。 两次载波迭代峰值均为5 000 次,第二次微调参数ε为0.000 1。
3.3.2 运算结果及分析
将上述参数代入模型进行运算,输出结果如表2、表3 及表4 所示。了56%,即大量非公交机动车出行者转移到公交出行。
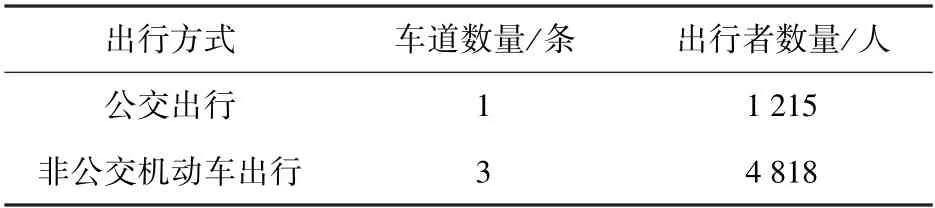
表2 一条公交专用道两种出行方式的出行者数量
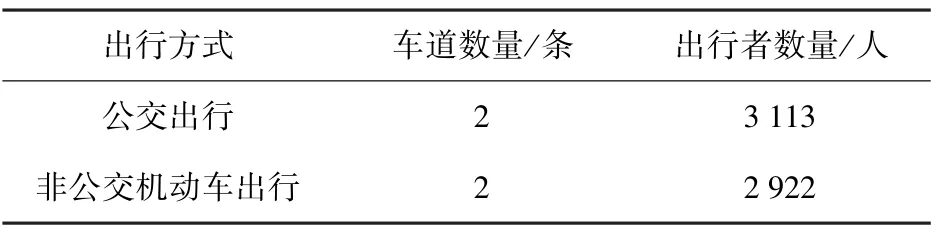
表3 两条公交专用道两种出行方式的出行者数量

表4 不同公交专用道数量条件下两种出行方式的出行费用
表4 表明,设置两条公交专用道时,由于非公交机动车道相应减少一条,若出行者原有出行方式不变,势必造成非公交机动车道的拥堵。 然而,由于非公交机动车道的拥堵,会吸引部分非公交机动车的出行者选择转向公交出行,因此使该两种出行方式的人均广义费用降低,交通系统的运行效率得到了提升。
对混沌算法的稳定程度进行检验时,在相同环境中将程序运行100 次,结果如图6、图7 所示。

图6 混沌算法的稳定度检验
图7 表明,尽管单次的人均成本差值存在较大差别,但程序运行100 次之后两者的差值只有0.004 1,与出行成本均值4.175 6 对比,只为其0.098 1%,也说明通过混沌优化算法所获得的出行人数分配结果有较好的稳定度。

图7 两种出行方式人均出行成本差值
4 结论
本文基于博弈论建立了双层规划模型,探讨了城市干路机动车道空间路权的动态分配方法,得出如下结论:在城市干路原有公交专用道的基础上再增加一条公交专用道,会吸引部分非公交机动车出行转向公交出行;通过优化城市干路机动车道空间路权的分配,能够有效提高公交出行分担率,降低交通系统的成本。
由于本文的研究对象局限于城市干路的机动车道,并未涉及到行人、非机动车以及其他道路类型的路权分配,研究结论也会与实际情况存在一定差异。希望能在本研究基础上开展试点工作,取得成效后再推广应用,为缓解城市交通拥堵、推动绿色低碳出行发挥作用。
