气囊式可调频动力吸振器性能研究

李 创，徐 伟，胡泽超，邱元燃

(1. 海军工程大学 振动与噪声研究所，湖北 武汉 430033；2. 船舶振动噪声重点实验室，湖北 武汉 430033)

0 引 言

被动式动力吸振器的有效吸振带宽较窄，无法满足激励频率变化较大情况下的减振需求，因此需要对吸振器施加主动控制来实现宽频带内的吸振。主动式动力吸振器分为全主动式和半主动式。由于半主动式动力吸振器具有耗能少、控制简单、稳定性好等优点，近年来得到了广泛研究。目前研究的成果有机械式、电磁式、新材料式和变质量-负刚度式半主动动力吸振器等。

以上结构设计主要适用于解决小型设备的振动问题，对于大型或超大型机械设备，需要获得较大质量比，上述吸振器存在作动力不足等问题。基于气囊大载荷特性，以气囊为刚度元件的半主动动力吸振器设计引起了广泛关注。Brennan利用气囊设计了一种半主动动力吸振器，通过改变气囊压力大小来调节吸振器刚度，拓宽了吸振器的工作频带，该设计可以提供较大的作动力，但其并未建立系统的动力学模型。靳晓雄设计一种应用于汽车发动机上的基于气囊的半主动动力吸振器，进一步建立系统的动力学模型，并对吸振效果进行仿真，但未分析阻尼因素对吸振效果的影响。为了拓宽气囊式动力吸振器的工作带宽，提高吸振器吸振效果和适用性，亟需建立完善的系统动力学模型。

本文提出一种气囊式可调频动力吸振器，以气囊作为刚度元件，通过调节气压来改变吸振器刚度，达到调节其吸振频率的目的。通过节流孔连接上、下2个气囊，调节节流孔大小改善该吸振器的阻尼特性，因此吸振器具有较宽的吸振频带和较好的吸振效果。同时由于气囊具备大承载特性，该吸振器的质量可以设计的足够大，能够提供较大的作动力，满足对大型设备的吸振需求。

1 结构原理

该吸振器由螺杆、气囊、质量块、节流孔、上顶板、下底板组成，如图1所示。中间质量块与上、下气囊固接，上、下气囊分别与上顶板和下底板固接。通过调节气囊压力，使吸振器固有频率与激励频率一致，从而抑制设备振动。阻尼是吸振器的重要参数，存在一个最优阻尼值使吸振器的吸振效果最优。该吸振器采用节流孔连接2个气囊，气囊振动过程中会在节流孔两侧形成压力差，气体在压力差的作用下流过节流孔产生阻尼效应，通过调整节流孔开度，可将阻尼控制在合适的范围，提高吸振效果。

图1 气囊式可调频动力吸振器结构Fig. 1 Structure of the frequency adjustable air-spring dynamic vibration absorber

2 理论模型

2.1 气室模型

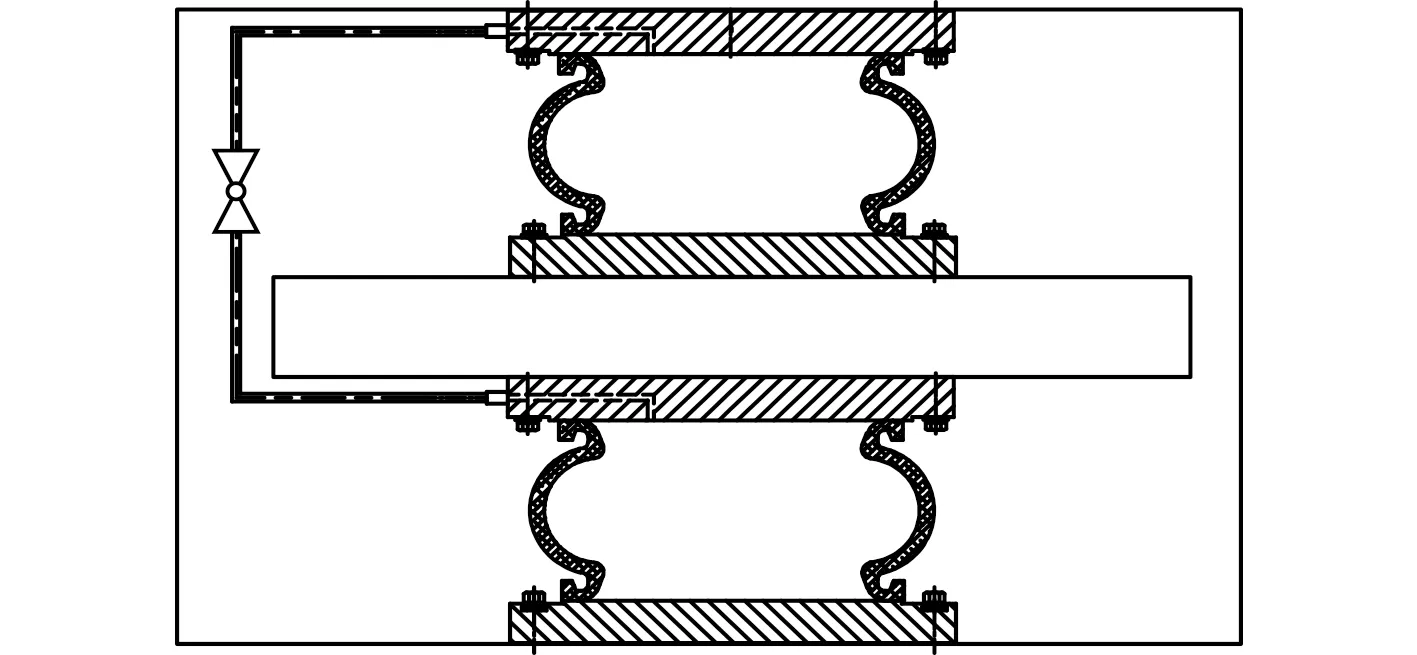
图2 气囊式可调频动力吸振器简化模型Fig. 2 Simplified model of the frequency adjustable air-spring dynamic vibration absorber

图3 气囊式可调频动力吸振器原理图Fig. 3 Schematic of the frequency adjustable air-spring dynamic vibration absorber

气囊式可调频动力吸振器简化理论模型如图3所示，上、下气囊可视作并联的刚度元件，K(ω,A)为下方气室复刚度，K(ω,A)为上方气室复刚度，忽略气囊囊体刚度，系统的的总复刚度可以用“气囊-节流孔-气囊”模型复刚度表示，即上、下气室的复刚度之和，其表达式为：

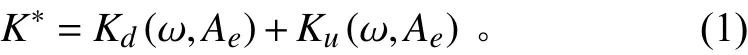
首先对下方气室进行分析，如图4所示，根据刚度定义得到其刚度表达式：

式中：A为下方气室有效面积，f为下方气囊垂向负载，为气囊位移，P为下方气室绝对压强，P为环境大气压强。

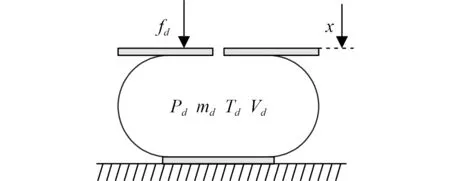
图4 下方气囊模型Fig. 4 The model of the lower air spring

假设下方气囊做微幅振动，则其有效面积A近似为定值，可以得到：

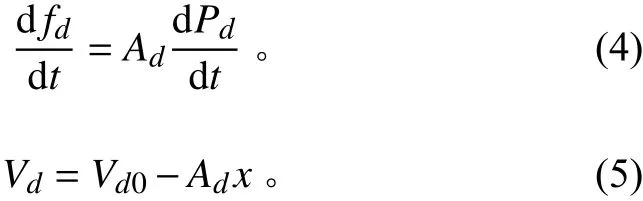
式中：V为下方气室体积，角标0代表其为初始值。

结合式（1）～式（6），可以得到下方气室刚度表达式：

假设工作气体为理想气体，根据理想气体状态方程，可以得到下方气室气体质量变化率为：

式中：和 κ 为气体常数和热力学常数；˙代表下方气室气体质量变化率；T，，P表示下方气室温度、体积和压强的初始值。

同理，如图5所示，可以得到上方气室气体质量变化率为：

式中：˙表示上方气室气体质量变化率：，，P表示上方气室温度、体积和压强的初始值。A为上方气室有效面积（近似为定值），f为上方气囊垂向负载，P为上方气室绝对压强。

图5 上方气囊模型Fig. 5 The model of the upper air spring

2.2 节流孔模型

节流孔的质量流量用˙表示，上、下气室气体的总质量不变，可得：

上、下气囊气室中的气体由于压力差通过节流孔相互流通，如图6所示，在气体交换过程中，气体流动的速度远远高于热量传递的速度，该过程可以视为绝热过程处理。根据文献[14]，流经节流孔的气体质量流量可以表示为：

图6 节流孔模型Fig. 6 The model of orifice

式中：=max(P,P),=min(P,P)，=sign(P-P)T+sign(P-P)T， A为 节流孔截面积，为 气体摩尔质量。

2.3 复刚度模型

将式（8）和式（9）进行傅里叶变换，得到上、下气室的频域质量流量表达式分别为：

由于气囊振幅较小，节流孔压力差只在一个很小的范围内变化，在平衡点对式（12）进行线性化，得到节流孔频域质量流量表达式：

式中：C为 节流孔的流量系数，通过实验测得。

假设初始状态上、下气室同温同压，即T=T=， P=P=。将式（13）～式（15）和式（10）～式（11）代入式（7），得到上、下气室的复刚度分别为：

式中：=V/V，表示下、上气室初始体积比，式K(ω,A)和K(ω,A)的实部表示系统的储存刚度，反映系统的刚度特性，虚部表示系统的耗散刚度，反映系统的阻尼特性。

3 复刚度数值计算

以JYQN-30 000型大载荷气囊为例，其各项参数如表1所示。根据式（16）和式（17），计算“气囊-节流孔-气囊”模型复刚度，结果如图7所示。

表1 模型参数Tab. 1 Parameters of the model

如图7（a）和图7（d）所示，随着节流孔开度的增大，系统的储存刚度“S”形曲线逐渐右移，耗散刚度峰值点的频率变大。图7（c）和图7（d）表明，随着气囊压力的升高，系统的储存刚度在低频区（0～1 Hz）基本保持不变，在高频区（12.5～100 Hz）线性增加，耗散刚度整体变大。分析可知，低频时气体流速较慢，2个气囊无障碍相通，导致系统储存刚度较低，此时无阻尼效应；中频（1～12.5 Hz）时，在压力差的作用下，气体通过节流孔在2个气囊之间快速流通，形成阻尼效应；高频时（12.5～40 Hz）气囊振动较快，气体在节流孔处形成阻塞，节流孔无气流通过，2个气囊处于隔绝状态，表明节流孔开度和气囊压力大小对该系统的储存刚度和耗散刚度有较大影响。

4 吸振性能分析

4.1 吸振范围分析

根据计算得到的系统刚度值，求出气囊不同初始压力下的吸振器固有频率，得到不同吸振器质量下的吸振频率范围，计算结果如图8所示。气囊初始压力由0.3 MPa变化到2.8 MPa，吸振器质量为0.5 t，1 t和2 t时的固有频率范围分别为15.1～46.1 Hz，10.7～32.6 Hz，7.6～23 Hz。

4.2 吸振效果分析

气囊式可调频动力吸振器可以通过调节节流孔开度来改善其阻尼特性，提高吸振效果。如图9所示，对于质量为100 t的主振动系统，吸振器质量为2 t，气囊式可调频动力吸振器可通过调整节流孔面积（A=4 cm）达到最优阻尼比=0.08，此时主振动系统的动力放大系数降低为原来的33%，而当阻尼比为0.02（过小）或0.31（过大）时，主振动系统的动力放大系数没有明显降低，甚至有所增加。

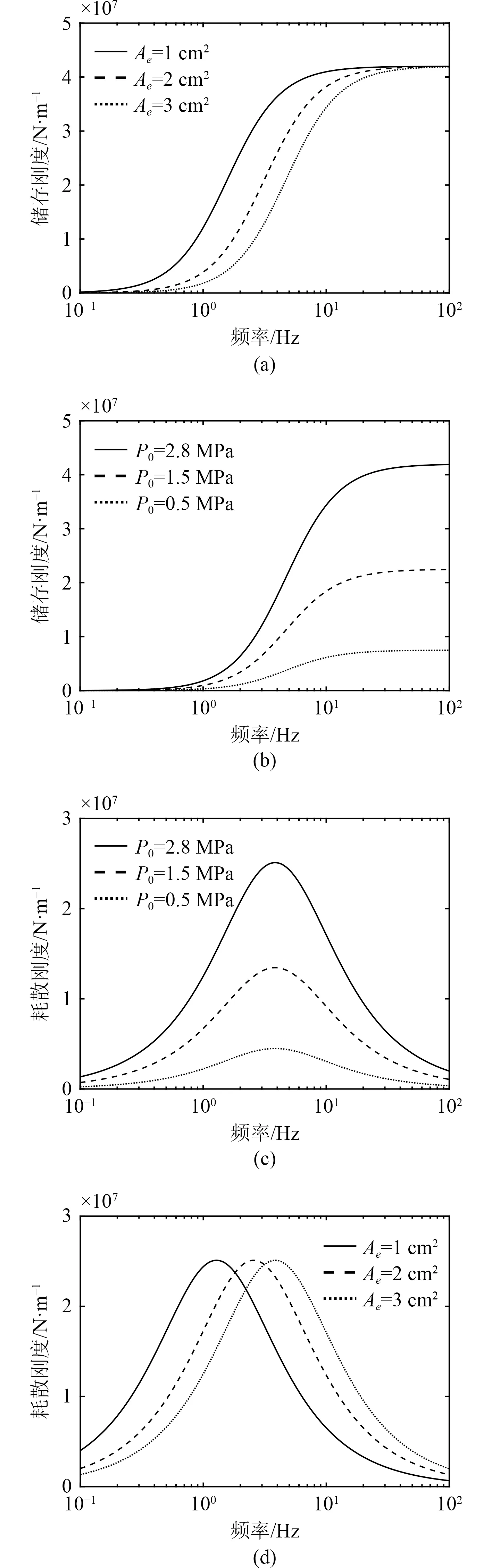
图7 复刚度计算值Fig. 7 Computational simulation of the complex stiffness

图8 气囊式吸振器吸振频率范围Fig. 8 Natural frequency range of vibration absorber

图9 阻尼比对吸振效果的影响Fig. 9 Influence of damping ratio on vibration absorption

吸振器质量是吸振效果的重要影响因素，小质量吸振器无法适用于大型和超大型机械设备。气囊式可调频动力吸振器利用气囊的大载荷特性，可以将吸振器质量调整至2 t，甚至更高，能够对上百吨的大型机械设备有效吸振。如图10所示，对于质量为100 t的主系统，当吸振器的质量为2 t时，在主系统固有频率处，主振动系统的动力放大系数降低为原来的28%。

图10 质量对吸振效果的影响Fig. 10 Influence of mass on vibration absorption

5 结 语

本文首次建立较为完善的“气囊-节流孔-气囊”复刚度理论模型，考虑了吸振器刚度和阻尼对吸振效果的影响，通过数值仿真探究不同节流孔开口面积、气囊气压对复刚度的作用，并对该吸振器的吸振范围、吸振效果进行仿真计算。结果表明，该吸振器对大型设备吸振效果显著，吸振带宽可达7.6～46.1 Hz，最高可将主系统振动降低至原来的28%。