机场进港旅客时间价值双加权K近邻预测模型

邢志伟，刘子硕，罗 谦+，文 涛，陈肇欣，代 军

(1.中国民航大学 电子信息与自动化学院，天津 300300； 2.中国民用航空局第二研究所工程技术研究中心，四川 成都 610041)

0 引 言

近年来，智能综合交通发展迅速，民航机场陆侧综合交通高效运行也成为行业关注的热点问题[1]。相比国外迪拜、亚特兰大等大型机场航班中转率超过50%，国内大型机场北京首都、广州白云等机场航班中转率只有约10%[2]，国内机场高比例的目的地直达进港旅客使得陆侧换乘客流庞大，从而对陆侧综合交通资源的高效运行和协同调度提出更高的要求。对机场而言，要做好陆侧资源协同调度的关键点之一就是应实时准确掌控进港旅客的流动态势。机场进港旅客到达口是旅客从航空换乘地面交通的关键节点，因此对到达口旅客人数进行短时预测是掌握进港旅客流动态势的基础。

对到达口旅客人数进行预测的关键是对旅客下机后的流动过程及态势进行建模。在航班落地至旅客到达航站楼聚散大厅过程中，机位距离远近直接影响旅客在航站楼内的步行时间，因此机位距离是预测模型中的重要影响因素；分析旅客下机流程，进港旅客与其它交通枢纽相比多了提取行李环节，因在行李提取过程中旅客提取行李的实际时间和数量难以采集，所以将行李总数作为影响旅客到达口人数预测的特征因素之一。根据旅客快速换乘的出行需求，航班落地、上轮挡、开舱门等时间信息决定了旅客何时能下机进入陆侧换乘区，在一定程度上影响了旅客的换乘心理和需求[3]，使得旅客出行选择和步行速度发生变化，这类时间信息可统一定义为航班信息时间以作用于预测模型。通过对上述旅客下机流动过程的特征信息量化建模后，可实现到达口旅客人数预测。

1 相关工作

研究者们已经提出了许多典型的客流预测模型，目前已经在回归模型[4,5]、机器学习模型[6,7]和混合模型[8,9]等方面取得了部分研究成果。在对进港旅客使用客流预测模型时发现不同航班旅客因存在步行距离、是否提取行李以及提取行李等待时间等因素的差异，因此不同航班旅客离开到达口规律存在较大差异。传统回归模型中，依靠历史数据建立统计模型的方法实现客流预测精度难以提高；机器学习模型中的K近邻算法可以通过筛选数据中的相关性数据样本，减小无关历史数据对预测的影响，以提高距离、行李提取等重要特征因素影响下的模型预测精度[10]。考虑到航站楼离港客流量短期的周期性变化易受到天气、航班延误等不确定因素影响，针对其复杂的非线性特点，以往有研究提出先用K近邻计算相匹配的历史航班，再用K近邻实现离港人数预测的双层K近邻算法，提高了离港旅客短时预测精度[11]。林培群等[12]面对地铁客流发展模式具有一定规律的特点，提出基于误差变化率的计算方式，从而自动获取合适K值提高预测精度。以上模型大多以客观环境因素特征作为模型输入，预测时忽略了时间导致的旅客主观因素对旅客流动态势的影响。

航班信息时间作为描述旅客主观感受的抽象化特征，可以通过构建时间价值函数的方式进行量化描述。时间价值函数最早由Kahneman等[13]提出，在金融经济学领域针对期望效用理论存在的整体风险预估不足，将随时间的收益定义为凹函数，损失定义为凸函数，从而对某项投资整体做出风险计算。在交通领域，近些年学者们展开对出行者在时间约束下的感知研究[14-16]。宗刚等[17]在居民出行中借鉴时间价值函数理论对居民时间成本加以考虑，提出累积前景理论更适用于出行方式研究，实现了居民出行不同交通方式时间满意度的整体感知计算。姚兰[18]选取通勤者在出行方式选择的两个参照点：行程所用时间和行程所需费用，借鉴时间价值函数中的收益与损失概念解决了上班者在通勤过程中不同目的地导致的感知数值差异的计算问题。

基于上述对时间价值的研究，本文通过刻画旅客对航班信息时间的感知模型，在传统K近邻算法的基础上，平衡主要因素的影响得到加权欧式距离，最终建立基于航班信息时间价值函数的双加权K近邻模型实现对进港旅客到达口的人数预测。

2 基于航班信息时间价值函数的双加权K近邻模型

根据上文对旅客下机后流动过程的影响因素分析，设计了如图1所示的到达口旅客人数预测思路。首先针对旅客下机至到达口的整体流程，提取机位距离、行李总数、航班信息时间作为进港旅客到达口人数的影响特征，构建航班信息时间价值函数。其次在传统K近邻算法的基础上改善K值的量化方法，将行李总数与时间价值函数量化后的航班信息时间与机位距离输入到改进的加权欧氏距离中，从而实现基于时间价值函数的双加权K近邻混合模型预测。

2.1 航班信息时间价值函数

将进港航班信息时间类比影响旅客主观心理变化的时间节点，航班的时间差异导致旅客感知数值发生变化，符合时间价值理论感知数值的变化准则，故将其作为航班信息时间特征的量化方法。假设进港航班的落地时间为ta， 上轮挡时间ts， 开舱门时间to， 第一位旅客步行至到达口时间tf与最后一位旅客步行至到达口时间tl为参考点时间。

定义国内进港航班旅客在进港换乘过程中，旅客随航班信息时间的心理感受和换乘需求变化的价值函数符合负值向正值过渡的分布规律，具有负值和正值感受非对称的特征。

航班信息时间价值函数如图2所示。

依据时间价值感知理论[19]，旅客在ta与ts之间时，受到航班业务节点时间的约束旅客不具有主动权，旅客想离开飞机的状态需求受到制约，于是产生损失感受，因此为负区间；当飞机停下后，旅客具有了自己的主动权开始收拾行李、排队下机，航班时间节点对旅客的下机需求约束逐渐弱化，旅客正值感受呈现上升趋势；开舱门后旅客完全具有主动权而进入航站楼，因此旅客的时间价值达到最大值；下机后因提取行李或其它随机因素(如寻找行李推车、接打电话等)影响旅客时间感知价值逐渐下降，当位于到达口时，旅客关注度由离开飞机转移到交通换乘，航班时间信息对旅客的约束逐渐消失，旅客的航班时间感受价值趋向于0。为方便描述，定义Ⅰ区为飞机滑行损失区，Ⅱ区为获得上升区，Ⅲ区为获得下降区。

根据航班信息时间价值函数定义，借鉴时间约束下感知数值的计算方法[20]，刻画旅客从航班落地至达到出口的时间价值感知过程，得到旅客的时间价值函数如下

(1)

根据航班信息时间价值函数的定义，为了将旅客的正感知表示为凹函数，负感知表示为凸函数得到0<αi≤1。 其中β表示损失规避程度，由前景理论的定义可知对于损失的感应比获得更敏感，所以Ⅰ区的斜率高于Ⅱ区。由之前总结，开舱门前旅客因具有主动权正感知迅速上升与开舱门后旅客排队下机正感知缓慢下降相比Ⅱ区比Ⅲ区斜率高，得到：β1>β2>β3>β4。

根据田丽君等[20]关于前景理论的探讨，以及所给β参数的利用得到旅客在ti时到达出站口时间的感知数值

(2)

同理在时间tf后每隔n分钟旅客到达出站口时间的感知数值也可求得。其中π-，π+分别是正感知与负感知所对应的权重，为各部分的时间价值函数的数值与总时间价值函数数值的比值。

tf由机位距离M决定，定义旅客步行的平均速度v， 可得

从表1可知，对于所提取的特征量具有2种缺陷的样本，神经网络完全能够识别出缺陷的存在，而只具有某一种缺陷的样本，神经网络存在识别错误。该错误主要是由于用于训练的样本数量不够导致对网络的训练不足。综合来看，神经网络的缺陷检测率达到了80%，说明采用此方法对勺子缺陷进行检测是可行的。

(3)

式中：Mi表示机位i至到达口的步行距离。

2.2 基于时间价值的双加权K近邻模型

式(2)量化了航班信息时间以构建航班信息时间价值函数，将其与行李总数共同作为特征输入到达口旅客人数预测模型。因为量化后的航班信息时间数值V(t) 与行李总数L(t) 对预测对象的比重是不同的，在构建模型时需要考虑特征数值在样本空间中的分布情况，因此本文设计了一种加权欧氏距离的方法量化特征权重。权重系数的定义如下

(4)

(5)

再根据加权欧氏距离得到预测值的K个近邻后，传统的K近邻将此K个近邻等权重看待，但距离小的近邻值在预测中应当占更大的权重，因此对K个近邻采取带权重的预测算法，得到基于时间价值的双加权K近邻模型(P-KNN)

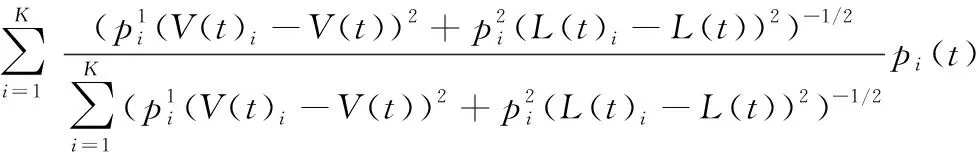
(6)

式中：p(t) 表示t时刻到达口旅客的预测人数，pi(t)(i=1,2,…,K) 表示在K个近邻点中，第i个点所对应历史时刻到达口旅客人数。

3 实证分析结果

3.1 数据来源与处理

表1 进港航班信息数据样例

远机位旅客下机后即乘坐摆渡车离开，与近机位直接从廊桥到达航站楼类比，中间没有等待摆渡车时间，且两辆摆渡车之间衔接紧密，因此只多了摆渡车运行时间。根据机场摆渡车运行服务水平评价，摆渡车的平均运行速度为20 km/h，可根据机场远机位摆渡车运行距离的测量值计算得到不同远机位摆渡车的运行时间。综上根据以上初始数据，对机位距离和航班信息时间特征进行量化。

假设旅客步行速度为1.2 m/s，设置预测时间跨度n=5 min，根据式(3)可计算出不同机位的tf， 根据表1可知ta、ts和to。 再根据航班信息时间价值函数，分别计算到达口旅客时间价值感知数值。

最终得到近远机位从tf开始，每隔5 min到达口旅客时间价值感知数值。以近机位为例，部分结果见表2。

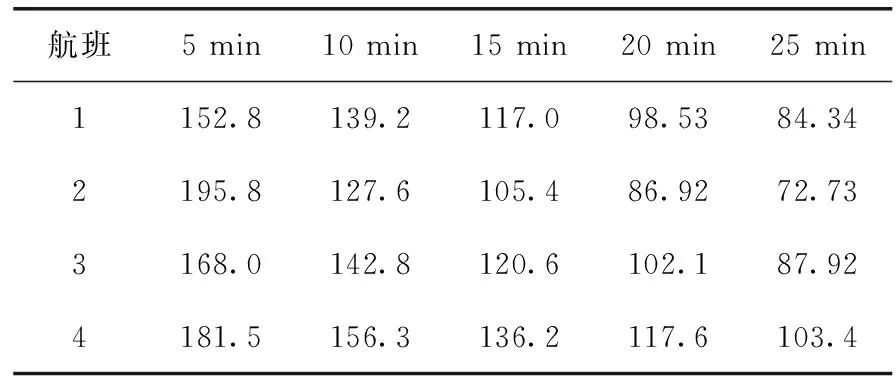
表2 近机位旅客时间价值感知数值(部分)

通过测试数据对模型的K值选取进行了实验测试，分析结果表明不同K值对模型精度的影响差异较大，如图3所示。最终选取误差最小的K=7作为模型参数。

3.2 模型输出与误差分析

以预测从tf后第5 min的人数为例，利用航班信息时间价值函数得到第5 min旅客时间感知数值以及第5 min行李总数动态化数值作为特征输入，出站口的人数作为模型输出。分别将近远机位数据组的后20组数据作为测试组，剩余数据作为实验组，得到20组测试航班中每个航班第5 min位于到达口的人数，同理预测得到每间隔5 min的到达口人数。在以上预测数据的基础上，选取近机位20组测试数据中表1样例数据每5 min的预测结果进行组合，如图4所示。

分析近机位到达口旅客人数预测图4发现，不同机位距离和行李数量的航班旅客在到达口的分布规律存在差异。究其原因，航班1、航班2因机位距离较近以及行李数量较小导致的行李处理时间短，使得不提取行李旅客与提取行李旅客短时间内集中出站，因此图4(a)、图4(b)出现了单个高峰。而航班3、航班4因为机位距离较远因此旅客集散过程更为离散，且航班行李数量较多导致行李处理时间较长，因此使得图4(c)、图4(d)不取行李旅客和提取行李旅客的分布规律在图形中出现了两个高峰。

远机位旅客一般由摆渡车分两批运送，时间分布较长。因第一批旅客到达航站楼后由于摆渡车在该机场送达位置距离到达口较近，因此与以上图4(a)、图4(b)近机位旅客分布规律相似，在短时间内出现了单个高峰。随着时间的推移，根据摆渡车运送距离和速度测算在第25 min～30 min处远机位航班两批旅客在到达口会发生客流重叠，于是远机位航班旅客呈现出两个相似高峰规律。如图5所示。

针对近远机位利用20组检验的预测与实际数据的值，使用均方根误差RMSE和拟合优度R2进行误差分析，并增加了机器学习的支持向量机(SVR)预测模型进行对比误差分析。以预测位于到达口较近的近机位旅客人数为例，计算基于时间价值的双加权K近邻模型的RMSE值以及拟合优度R2的值与SVR模型和传统的K近邻模型对比效果如图6、图7所示。

从图6、图7可以分析得到，基于时间价值的双加权K近邻模型与传统的K近邻模型和SVR模型比较，均方根误差RMSE的值最小且其性能平均提高了5.8%。同时拟合优度R2的值最大且其拟合优度提高了7.2%，显示了双加权的K近邻算法具有良好的预测性。

4 结束语

通过对国内某大型机场2019年1月～2019年4月期间的国内航班进港信息进行分析，对单航班进港旅客到达口人数进行预测，最终得到以下研究成果：

(1)提取影响旅客到达口的因素并考虑对预测对象的比重不同，赋予因素不同的权重从而改进欧式距离，实现了K值选取方法的优化；

(2)针对航班信息时间复杂和难以量化的问题，提出了进港航班旅客的时间感知价值刻画方法；

(3)构建基于进港航班信息时间价值函数的双加权K近邻混合模型，均方根误差RMSE的性能和拟合优度R2的值与其它方法相比均有所提高。

进港航班信息时间价值函数的双加权K近邻模型虽表现出较好的预测效果，但仍存在缺少特征数据、特征体系不完善等问题，未来，随着空港交通体系的信息化发展不断累积特征数据，完善模型特征体系，从而进一步提升方法的有效性和适用性。