基于变步长扰动观察法结合改进天牛群优化算法的三步复合光伏最大功率跟踪算法
2022-10-17刘文锋李昂
刘文锋,李昂
(陕西理工大学电气工程学院,陕西 汉中 723001)
太阳能发电以其绿色清洁、安全稳定等特性,成为可再生能源发电中发展最迅速、规模最大的产业[1]。太阳能发电中一般采用最大功率点跟踪(maximum power point tracking,MPPT)技术,跟踪其最大功率点,减少功率失配损失,提升发电效率。
在局部遮阴(partial shading condition,PSC)情况下,即光伏阵列所受光照和工作温度不均匀时,光伏系统的功率-电压(P-U)曲线往往呈多峰状态[2-3]。此时,局部寻优能力较强的传统MPPT 方法,如扰动观察法、电导增量法,易陷入极大功率点[2,4-5],使得功率失配损失。而改进后的变步长扰动观察法(improved perturbation and observation,IP&O)等算法,提升了其跟踪速度,但仍然易陷入局部最优[5-6]。
为此,基于智能优化算法的MPPT 方法近年来颇受关注[4,7]。文献[8-15]将粒子群、差分进化、蚁狮、授粉、天牛群等智能优化算法应用到MPPT 方法中,虽然能较为准确地跟踪到最大功率点,但跟踪速度并不理想、且造成较大的功率波动。文献[16-18]提出了将粒子群算法、布谷鸟算法和扰动观察法分别结合的PSO-IP&O、CSA-P&O、CSA-IP&O 算法,这些算法是前期为智能优化算法,后期为传统算法的两步复合算法,跟踪速度虽有所提升,但在初期全局寻优时,功率波动较大、收敛速度较慢的缺陷依然存在。
基于以上研究,本文将变步长扰动观察法和改进天牛群优化(improved beetle swarm optimization,IBSO)算法相结合,提出一种基于IP&O-IBSO 的三步复合MPPT 算法。第一步,使用IP&O 快速跟踪到最后一个极大功率点,并根据复杂光照环境下光伏系统的输出特性[3,7],利用此点功率值动态调整IBSO 算法的电压搜索范围;第二步,利用IBSO 算法优越的全局寻优能力[13],进行最大功率点的全局搜索,避免跟踪陷入局部最优;第三步,在跟踪到最大功率点附近后,再次切换IP&O 算法,避免跟踪过程中的功率振荡,并加快收敛速度,进而准确且快速地跟踪到最大功率点。在MATLAB/Simulink中将此算法与IP&O、BSO、CSA-IP&O 算法进行对比分析,结果表明,本文算法跟踪速度更快,精度更高,功率波动更小。
1 局部遮阴下光伏系统多峰输出特性
图1 为多种情况下光伏系统I-U、P-U曲线,即一个4×1 光伏阵列在无遮阴的标准测试条件(standard test conditions,STC)下,以及3 种光照不同遮阴(PSC)情况下的I-U、P-U曲线,并注明了几种不同环境下各光伏板所受光照强度。图1 中:Pmpp为系统最大功率;Impp为光伏系统最大功率点电流;Iph为光伏系统光感电流;Umpp为光伏系统最大功率点电压。光伏阵列中每个组件皆选用MATLAB/Simulink 中TP250MBZ 光伏组件,其最大功率Pmax=249 W,最大功率点电压USTC=30 V,最大功率点电流ISTC=8.3 A。
由文献[3,7,19,20]和图1 可知,若光伏系统由y个光伏组件串联组成,在局部遮阴下,至多有y个极大功率点(峰值),这些可能出现的的极大功率点的电压值近似分布为:
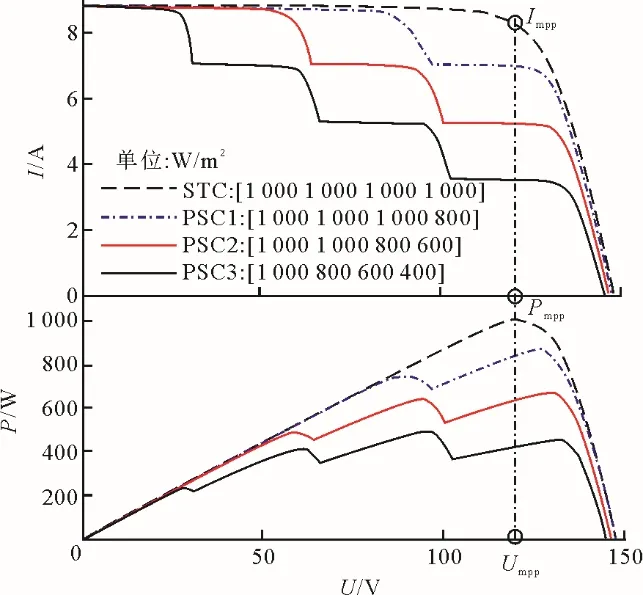
图1 多种情况下光伏系统I-U、P-U 曲线Fig.1 The I-U and P-U curves of the PV system in various situations
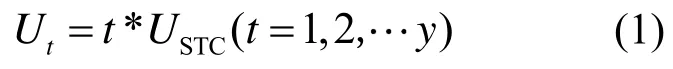
式中:USTC为单个光伏组件的最大功率点所对应的电压;t为光伏系统当前极大功率点的序号。
从图1 可知,标准测试条件下光伏系统的P-U曲线为单峰,此时最大功率为各单个光伏组件最大输出功率的叠加。当光伏系统所受光照越不均匀,其P-U曲线峰值越多且越明显,最大功率越小,此时最大功率点可能是y个峰值中的任何一个。从其I-U曲线可知,电流随电压的增大而减小,光照越不均匀,电流减小的越快。
2 基于IP&O-IBSO 的三步复合算法
2.1 变步长扰动观察法
IP&O 是将扰动观察法的跟踪步长与功率差相结合的方法。如式(2)所示,先计算出光伏系统受扰动前后输出功率的差值ΔP,若ΔP<0,则下次寻优时,电压扰动方向为相反方向;若ΔP>0,则下次寻优时,电压扰动方向为当前方向[2,6,18,20]。
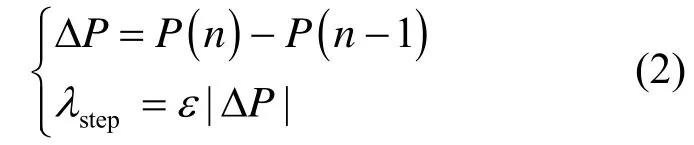
式中:P(n)为第n次扰动时的输出功率;P(n-1)为第n次扰动前的输出功率;λstep为跟踪步长;ε为步长系数。
由式(2)可知,将步长λstep与功率差ΔP结合后,IP&O 前期λstep较大,跟踪速度较快;后期λstep逐渐减小,不会在最大功率点附近产生较大功率波动,减少功率失配损失。
2.2 改进天牛群优化算法
天牛须搜索(beetle antennae search,BAS)算法是2017 年提出的基于天牛觅食行为的智能优化算法。天牛在觅食时,通过2 条须感应气味浓度寻找食物具体位置。若左须感应到的气味浓度小于右须,就向右移动,反之,向左移动,天牛模型如图2 所示。将其运用在MPPT 方法中,天牛须位置代表占空比,气味浓度代表光伏系统的输出功率[21]。
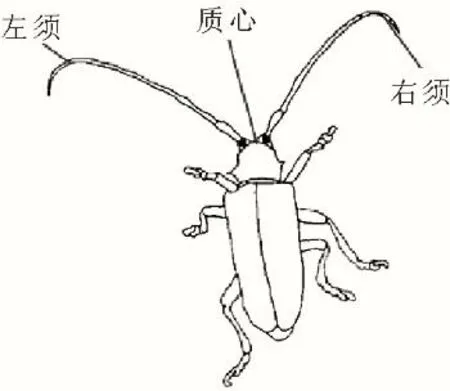
图2 天牛模型Fig.2 The beetle model
BAS 算法在解决多极值问题时易陷入局部最优,将其应用到MPPT 中,应对局部遮阴时,并不能准确的跟踪最大功率点。而文献[13]借鉴粒子群的群体优化思想,将BAS 算法推广到天牛群优化(beetle swarm optimization,BSO)算法,虽然准确性大有提升,但快速性仍有待提高。
本文提出的IBSO 算法,根据复杂光照环境下光伏阵列输出特性[3,7],利用初期IP&O 算法跟踪结束时的功率值,动态调整BSO 算法中各天牛的初始位置和搜索范围,再进行最大功率点的全局跟踪,以加快跟踪速度,提高跟踪精度。
图3 为IP&O-IBSO 算法的搜索范围趋势,采用图1 中PSC1、PSC3 2 种局部遮阴情况的P-U曲线进行分析,当算法前期采用IP&O 时,根据Boost电路特性[20,22-24]可知,若设置步长系数ε和初始占空比D0极小,则电压跟踪方向为从大到小,迅速跟踪到最后一个极大功率点Py后,若其对应电压为Uy,则此时最大功率点电压Umpp≤Uy,故以Uy为电压搜索上限,Dy为占空比(天牛位置)下限。
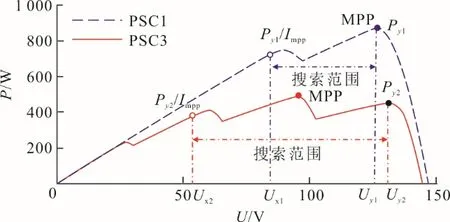
图3 IP&O-IBSO 算法的搜索范围趋势Fig.3 Trends in search range of the IP&O-IBSO algorithm
此时光伏系统最大功率点Pmpp与Py的关系为:
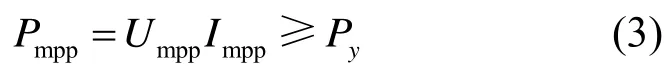
式中:Impp为光伏系统最大功率点电流,由图1 可知当光伏阵列处于无遮阴标准测试条件下,单个光伏组件最大功率点电流ISTC=Impp。
根据式(3),可得:

式中:Ux为电压搜索下限;Dx为占空比(天牛位置)上限;RL为负载电阻;Ix为光伏系统在Ux下输出电流,为便于计算可取Impp;天牛均匀分布于(Dy,Dx)之间。
由式(4)和图3 可知,IP&O 跟踪到Py后,Py越大,本文算法的电压搜索下限Ux越大,电压搜索范围越小,可得到较快跟踪速度;反之,Py越小,电压搜索范围越大,可保证跟踪精度。
IBSO 算法的具体寻优步骤为:
步骤1) 创建天牛须朝向的随机向量,可表示为:

式中:rand()为随机函数。
步骤2) 通过式(3)生成各天牛初始位置。
步骤3) 确定各天牛左、右两须xl、xr的坐标:
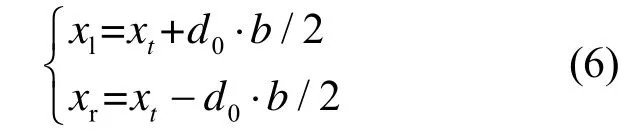
式中:xl和xr分别为右须和左须第t次迭代时的位置坐标;xt为第t次迭代时的质心坐标;d0为两须间距离。
步骤4) 各天牛比较左右两须的食物浓度,确定其各自的移动方向和距离:

式中:xt、xt+1分别为天牛当前、移动后的质心位置;sign()为符号函数;δt、δt+1分别为当前和下一次迭代步长;μ为收缩系数,μ∈(0,1)。
步骤5) 记录每一次所有天牛须中的最大气味浓度,若有2 次最大浓度差小于阈值,则输出最佳天牛须位置;否则,返回步骤3)。
2.3 基于IP&O-IBSO 的三步复合MPPT 算法
2.3.1 算法的重启条件
当光伏组件所受光照度或工作温度突变,导致光伏系统输出功率发生变化时,将重启MPPT。光伏系统输出功率变化量ΔPv 可表示为[18,20,25]:
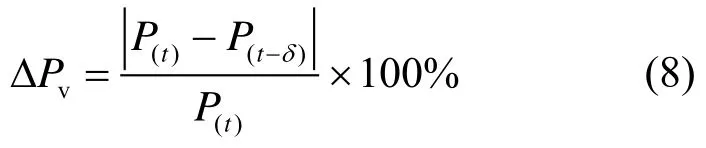
式中:P(t)和P(t-σ)分别为当前输出功率和σ前的输出功率;σ为时间间距;设定σ=0.02 s,ΔPv>2%时重启此MPPT 方法。
2.3.2 算法的切换条件
本文算法分为3 步,故有2 次切换,第1 次是在IP&O 跟踪到Py后引入IBSO 算法,以进行全局的最大功率点跟踪,保证其准确性;第2 次是在IBSO 算法全局寻优到最大功率点周围后,切换IP&O 算法,以减小振荡和加快跟踪速度,保证其快速性。基于IP&O-IBSO 的三步复合算法流程如图4 所示。
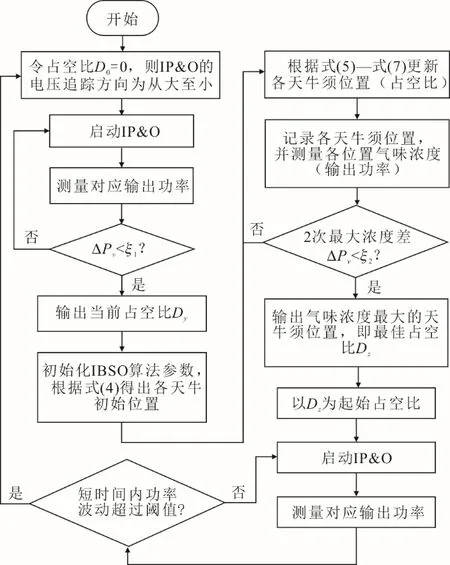
图4 基于IP&O-IBSO 的三步复合MPPT 算法流程Fig.4 Three-step compound MPPT algorithm based on IP&O-IBSO
图4 中:ΔPv 为通过式(8)计算出的跟踪最大功率点时的功率变化量;此时设定σ为0.002 s;ξ1为终止IP&O 算法的阈值,设为0.008;ξ2为终止IBSO算法的阈值,设为0.02。
3 仿真分析
在验证MPPT 算法有效性时,常采用由4×1 光伏阵列和Boost 电路组成光伏系统进行仿真[18,20,26]。本文将MATLAB/Simulink 中4 个TP250MBZ 光伏组件串联组成光伏阵列,该光伏阵列组件光感电流Iph=8.83 A,最大功率Pmpp=995.4 W,最大功率点电流Impp=8.3 A。其仿真模型如图5 所示。
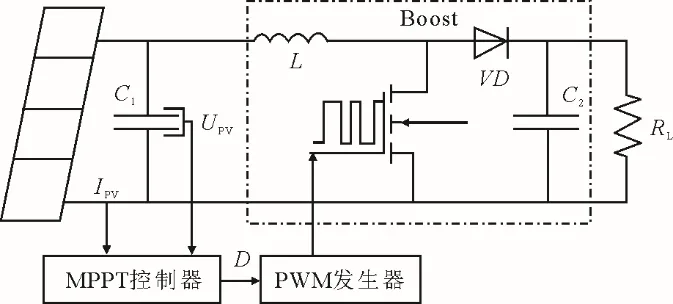
图5 光伏系统仿真模型Fig.5 Simulation model of the photovoltaic system
在此模型中,将本文算法与IP&O、BSO、CSAIP&O 3 种算法进行对比。为体现算法对比的公平性,特将4 种方法中所有IP&O 算法的ε设为0.000 75;将BSO 和CSA-IP&O 算法初始占空比都设为0.1、0.3、0.5、0.7,电压、电流采样时间为0.001 s。
3.1 静态局部遮阴下的功率跟踪
设置局部遮阴情况下各组件所受光强依次为400、600、900、1 000 W/m2,工作温度为10、15、20、25 ℃,此时光伏阵列的P-U特性曲线如图6 所示,最大功率点为499.8 W。
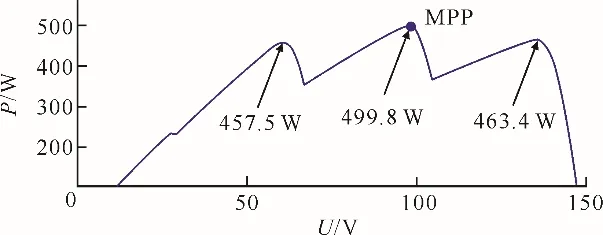
图6 静态局部遮阴下光伏阵列的P-U 特性曲线Fig.6 P-U characteristic curve of the photovoltaic array in static PSC
在此情况下,4 种算法的输出电压、输出功率曲线如图7、图8 所示。由图7 可知:静态局部遮阴下,IP&O 算法收敛速度快,但并未跟踪到最大功率点电压97.4 V,而是跟踪到了极大功率点电压136.5 V;BSO、CSA-IP&O 算法都跟踪到了最大功率点电压,但收敛速度较慢,电压振荡时间较长。本文算法在前期使用IP&O 算法先跟踪到极大功率点电压136.5 V,再根据此点功率值,调整IBSO 算法的电压搜索范围,进行全局寻优,成功跟踪到了最大功率点电压附近,最后再次切换IP&O 算法,使收敛速度加快,后期电压振荡减小。
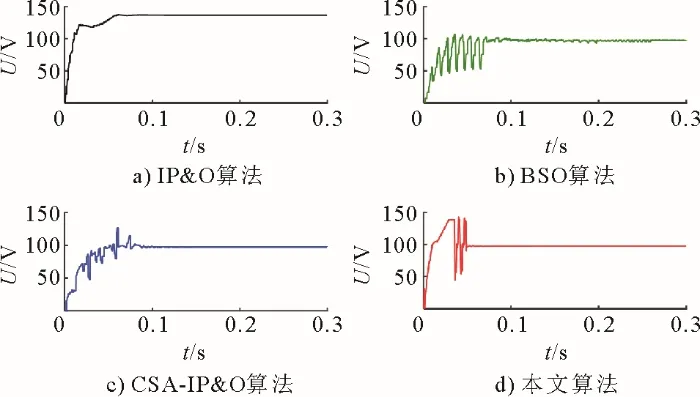
图7 静态局部遮阴下的输出电压对比Fig.7 Output voltage comparison in static PSC
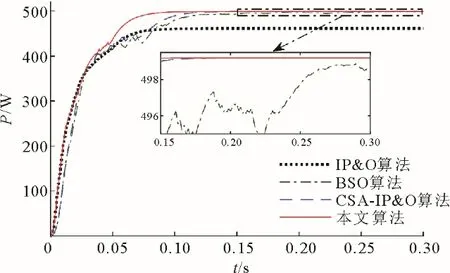
图8 静态局部遮阴下的输出功率对比Fig.8 Output power comparison in static PSC
由图8 可知:静态局部遮阴下,IP&O 算法陷入极大功率点;BSO、CSA-IP&O 算法跟踪速度较慢;本文算法跟踪速度最快,且跟踪精度最高。
3.2 动态局部遮阴下的功率跟踪
表1 为3 种工作环境参数。在Simulink 中模拟光伏组件处于表1 所示的3 种局部遮阴情况的P-U曲线,结果如图9 所示。
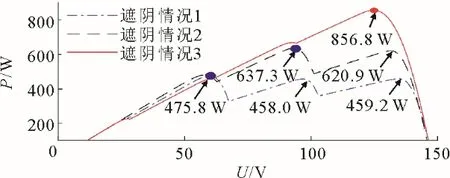
图9 不同遮阴情况下光伏系统的P-U 特性曲线Fig.9 P-U characteristic curves of the photovoltaic system at different PSCs

表1 3 种工作环境参数Tab.1 Parameters of three kinds of working environments
令光伏系统顺序历经3 种遮阴情况,每次变化持续0.5 s,在此情况下,4 种算法的输出电压、输出功率曲线如图10、图11 所示。
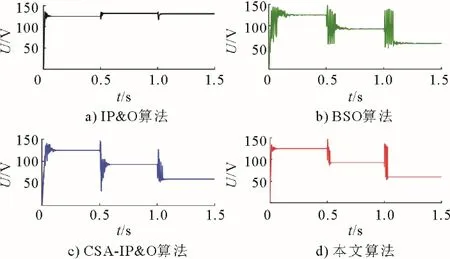
图10 动态局部遮阴下的输出电压对比Fig.10 Output voltage comparison in dynamic PSC

图11 动态局部遮阴下的输出功率曲线对比Fig.11 Comparison of output power in dynamic PSC
由图10 可知:在动态局部遮阴下,与IP&O 算法相比,本文算法不易陷入局部最优;与BSO、CSAIP&O 算法相比,本文算法利用IP&O 算法缩小了电压搜索范围,故IBSO 算法全局寻优时,跟踪速度大幅加快,且电压振荡减小。
由图11 可知:在动态局部遮阴下,IP&O 算法在遮阴情况2、遮阴情况3 时都陷入了极大功率点;BSO 和CSA-IP&O 算法在3 种情况下都能跟踪到最大功率点,有较高的跟踪精度,但跟踪速度较慢,且功率振荡较大;本文算法跟踪精度始终最高,跟踪速度最快,且在跟踪过程中功率振荡极小。
3.3 结果统计与分析
智能算法具有随机搜索特性,即每次最大功率点跟踪的精度和速度上可能略有不同。为了更客观地分析各算法的性能,将本文4 种算法在上述静态、动态局部遮阴情况下独立运行20 次,然后进行统计对比,详见表2。
由表2 可知:在静态、动态局部遮阴情况下,IP&O 算法收敛速度快、功率振荡小,但易陷入极大功率点;BSO 算法、CSA-IP&O 算法跟踪精度较高,但跟踪速度慢、功率振荡大;本文算法跟踪精度高,跟踪速度相较BSO 算法、CSA-IP&O 算法分别缩短了76%、48%以上,且功率振荡较小。
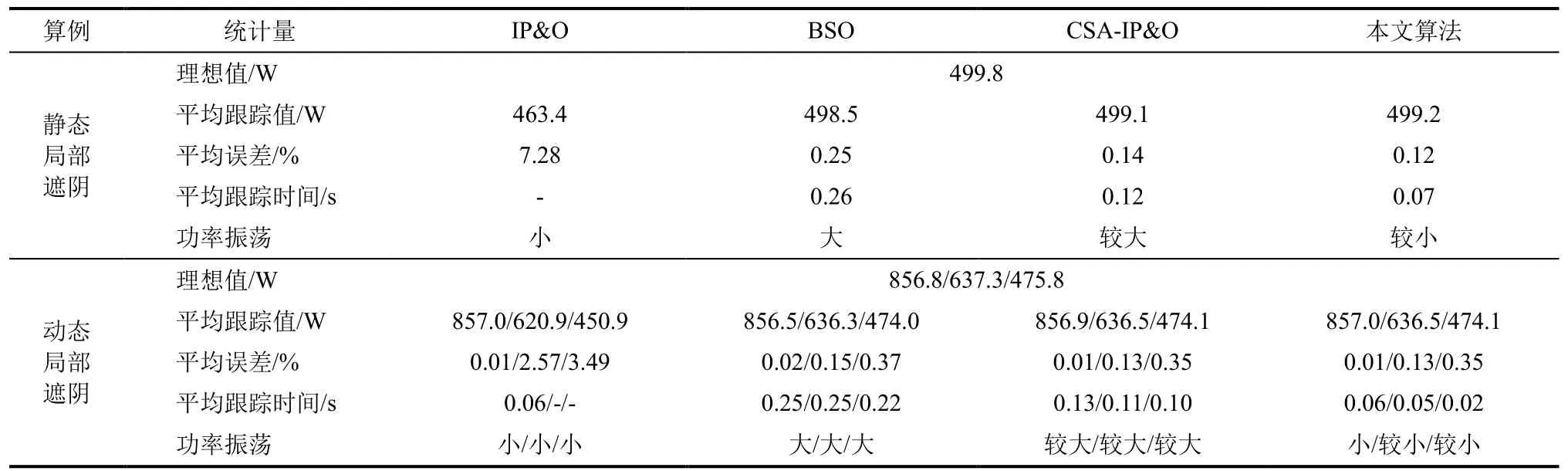
表2 4 种算法在静态、动态局部遮阴情况下性能比较Tab.2 Performance comparison of four algorithms in static and dynamic local shading
4 结论
本文在分析局部遮阴下光伏系统多峰输出特性的基础上,提出了基于IP&O-IBSO 算法的三步复合MPPT 算法。仿真结果表明:
1)本文算法相较于传统算法(IP&O),不易陷入局部最优,能准确地跟踪到最大功率点,准确性有较大改善。
2)本文算法相较于智能优化算法(BSO)和两步复合算法(CSA-IP&O),在保证准确性的前提下,又极大地提高了其搜索速度,而且跟踪过程中振荡更小。
