高风电渗透下电网调峰运行时的频率稳定控制策略研究
2022-10-17郭良杰王德林牛景瑶孙超
郭良杰,王德林,谢 棚,牛景瑶,喻 心,孙超
(西南交通大学电气工程学院,四川 成都 611756)
近年来,高比例新能源并网改变了电网中的电源结构比例。以风电和光伏为代表的可再生能源通过电力电子设备接口大量并网,将会导致电网惯性降低,增加电网在遭遇故障扰动下发生频率失稳的风险[1]。新时代下可再生能源的接入规模将会影响我国电力系统稳定性[2-3],而频率稳定作为电网安全运行的先决条件,不参与调频的可再生能源发电比例越高,越不利于电力系统的频率稳定控制[4]。因此,如何保障电网在调峰运行时的频率稳定控制尤为重要。此外,新能源发电是随机和不可控的,这增加了电网在调峰运行时的调频压力,影响系统运行安全性。
随着新能源发电的迅猛发展,火电机组亟需进入调峰状态以提高新能源并网消纳能力。文献[5]基于火电机组参与电网深度调峰的背景下,结合经典的PID 控制方法并通过机理分析提出实时变参数控制方法,实现了火电机组深度调峰运行时与可再生能源的协调控制。文献[6]考虑新能源接入对系统频率特性的影响,将限幅环节引入到调峰火电机组中,仿真分析表明限幅环节动作时会恶化调峰机组的频率特性。文献[7]通过分析风电机组的一次调频能力和火电机组的深度调峰能力之间的关系,以满足经济最优为目标,建立了风火联合参与调频的负荷优化分配模型,缓解了系统的调峰压力。
文献[8]针对大规模并网的风电波动功率对电力系统频率扰动的问题,提出了根据分频原理的机组动态一次调频控制方法,在2 区域系统中进行了仿真验证。在风电并网渗透率逐年提高的背景下,文献[9]基于分布式模型预测控制原理,提出了一种含风电的AGC 系统控制策略,实现了风电场参与系统调频,从而降低了常规机组的调频压力。此外,张剑云等[10]分析了电网稳定性和稳态频率误差,提出了新能源参与频率稳定控制的2 种方式,并对其进行理论分析和仿真验证。Bevrani 等人[11]在计及新能源发电的LFC 模型中仿真得出:在高风电渗透率的情况下,风电自身出力的波动会导致系统调频过程中最大频率偏差变大。上述文献从不同角度分析了大规模风电并网下系统的频率特性和控制策略,但是对高风电渗透下电力系统调峰运行时的频率特性分析较少,同时也未深入研究电网调峰运行时的频率稳定问题和对应的解决措施。
为积极推动我国能源转型,提升可再生能源并网的消纳能力,常规火电机组有必要积极开展灵活性改造,在降低其最小技术出力的同时为新能源出让并网运行空间[12]。已有研究表明,火电机组处于调峰运行时,火电厂的运营成本会随着风电渗透率的增加而提高[13]。文献[14]根据影响火电机组调峰能力的因素,建立相关的电力系统能源效率模型,提供了调峰机组多角度经济性分析的方案,使得系统在经济性运行的前提下能有足够的调峰裕度。由于目前对火电机组的深度调峰研究还处于初步阶段,较多的文献还是针对深度调峰运行的影响因素、安全性以及经济性进行分析,而关于深度调峰后的负荷调节和频率调节等功能还未进行过深入研究。对此,本文在传统AGC 模型中引入了新能源渗透率,细化了常规火电机组调峰时的AGC 频率响应模型,并且对火电机组2 种典型调峰方式和风电调频策略进行了分析研究。在火电机组层面探讨哪种调峰方式有利于频率稳定,在风电机组层面研究哪种风电调频策略有助于提高系统调峰运行时的频率调节能力,并基于以上2 个层面提出了解决电网调峰运行时的频率稳定问题的新方法。
本文从挖掘传统火电机组二次调频能力的角度出发,针对高风电渗透率下电力系统调峰运行时的频率稳定问题展开研究,建立火电机组处于调峰运行下的AGC 系统模型。首先,在传统的AGC 系统频率响应模型中引入了新能源渗透率、调速器死区和发电机出力速率约束这些非线性环节,进行频率特性分析;其次,研究系统电源侧2 种典型的调峰方式对电网频率调节的影响差异;最后,引入改进的风机综合惯性控制策略,在改造后的4 机2 区域系统中进行仿真验证。
1 电网AGC 系统频率响应的数学模型
1.1 常规火电机组AGC 频率响应模型
电力系统具有高度非线性与时变特性,虽然可以使用一组微分代数方程组来详细描述每台机组的频率特性及网络功率的变化情况,但是只能通过迭代积分的方法进行求解,无法通过解析解揭示系统频率特性的内在机理。
根据电力系统领域的相关文献[15-16],单区域再热式火电机组主要包括调速器、涡轮机、同步发电机及负荷和调频控制器等环节,可以聚合简化为图1 所示的AGC 系统频率响应模型。图1 中,Bi和Ri分别表示系统区域i的频率偏移系数和等值火电机组的调差系数。
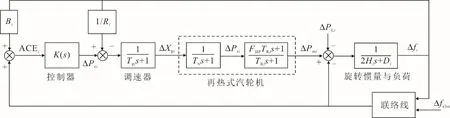
图1 单区域火电机组简化等值聚合AGC 模型Fig.1 The simplified equivalent aggregation AGC model for single-zone thermal power unit
联络线交换功率的变化会影响到互联系统的功率平衡,遭受负荷扰动时,根据联络线功率和频率的变化量,参考各个区域的动态响应特性,即可确定发生扰动的控制区。然后电网AGC 系统会按照相应的调节标准产生指令信号,调频器根据该指令信号作用于调速器以使得调速器产生位置增量ΔXgi;在再热型汽轮机中,汽轮机输出的机械功率会随调速器汽阀位置的变化产生ΔPmi的变化量,从而使得同步发电机改变出力补偿系统的功率失衡。电力系统负荷频率控制的目标就是添加相应的控制器使得扰动ΔPL对Δf的影响最小。
忽略系统网损的前提下,考虑同步发电机与负荷的动态特性,等值发电机的传递函数H(s)为:
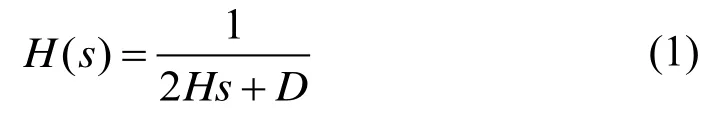
式中:H为系统的转动惯量系数;D为系统的旋转阻尼系数;s为对时间的微分算子。
再热式汽轮机考虑了中间再热汽容积效应和高压蒸汽这些环节,在蒸汽再热回流的过程中能有效提升蒸汽的利用率。当系统中含若干再热型火电机组时,可以利用加权等值的方法对若干台机组进行聚合,因此再热式汽轮机的传递函数M(s)为:
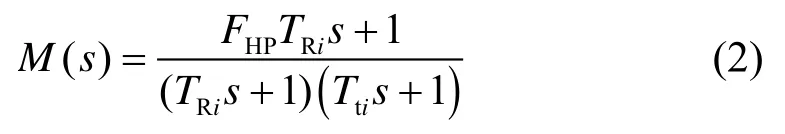
式中:FHP为等值汽轮机高压缸占汽轮机总输出功率比值的聚合参数;TRi为再热时间常数;Tti为汽轮机特征系数。
1.2 调速器死区环节
实际系统中火电机组的调速器死区对于频率振荡的影响不可忽视,设置合适的调速器死区有利于延长调速器的使用寿命。文献[17]基于单机等值系统中3 种不同类型的调速器死区对频率波动的影响展开研究分析,通过仿真验证了带有无阶跃死区或有阶跃死区的系统发生频率振荡时不会降低其稳定性。普通型死区在实际系统中应用最广泛,因此本文主要考虑调速器无阶跃死区。
调速器是火电机组中最基本的控制元件,主要是调整机组的转速及分配机组间的负荷,其数学模型可用传递函数W(s)表示为:
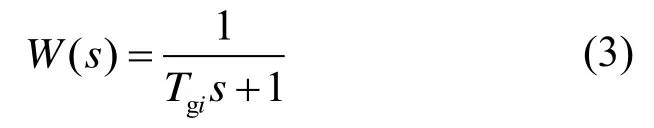
式中:Tgi为调速器时间常数。在实际系统中调速器只有在控制输入信号达到一定阈值时才会动作,设置合适的死区阈值将显著提高系统的频率控制动态特性[18-19]。因此需要在图1 系统模型调速器中加入无阶跃死区环节,无阶跃死区特性如图2 所示。

图2 调速器无阶跃死区特性Fig.2 The characteristics of speed governor without step dead zone
图2 中:h为调速器死区动作的临界阈值;X和Z分别为非线性环节的输入和输出。调速器无阶跃死区环节的输入与输出可用如下函数来表示:

给该非线性环节一个正弦输入信号X=Asinω0t,然后采用描述函数法对输出Z进行线性化[20],通过傅里叶级数展开表达式F,取前3 项可得:
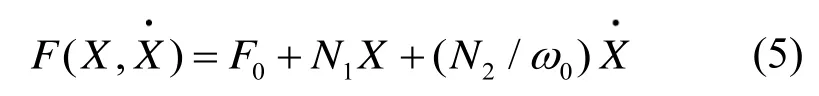
式(5)中各项系数分别为:

结合式(3),可得到线性化后的含无阶跃死区的调速器传递函数Wg(s)为:
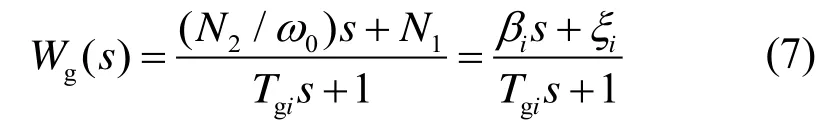
式中:βi为傅里叶级数展开后的非线性项系数,且βi=N2/ω0;ξi为傅里叶级数展开后的线性项系数,且ξi=N1;ω0为输入正弦波的频率。
1.3 含GRC 的再热汽轮机模型
实际AGC 系统中,火电机组是通过蒸汽推动汽轮机带动发电机调节出力的,为了确保汽室压力和锅炉温度等因素处于正常工况下,需要给发电机组的出力速率施加一个上限,即发电机组出力速率限值(generation rate constraint,GRC)。GRC 环节是另一个影响火电机组运行性能的重要因素,含GRC 的再热式汽轮机模型如图3 所示。

图3 含GRC 的再热汽轮机模型Fig.3 The reheat steam turbine model with GRC
为了获得准确的频率控制动态特性,在图1 系统模型中考虑了GRC 的再热式汽轮机模型。经过图2 和图3 的非线性环节得到的改进AGC 系统模型就是典型的非线性组合系统。
实际火电机组中,发电机出力速率VPmi最大变化值一般为0.15 pu/min,即:
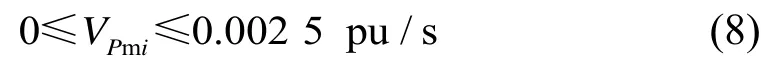
1.4 联络线模型
由于实际系统中负荷的波动会导致区域之间功率失衡,为此需在各个控制区域之间设置联络线用于功率的交换和平衡,来保证电力系统运行的稳定性和频率一致性。
定义联络线的功率同步系数TI-II为:
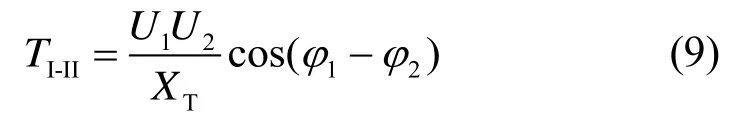
式中:U1和U2分别为区域I和II的等效发电机机端电压;φ1和φ2为对应区域等效发电机的功角;XT为2 区域间的联络线等效阻抗。
可知,电网正常运行情形下当相角发生微小偏移时,推导出区域间联络线交换功率的变化量为:
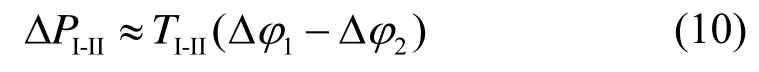
式中:ΔPI-Ⅱ为联络线交换功率相对计划值的偏差。
由于Δφ=2π∫Δfdt,然后根据式(9)和式(10)可得到区域Ⅰ和Ⅱ间联络线交换功率增量方程为:
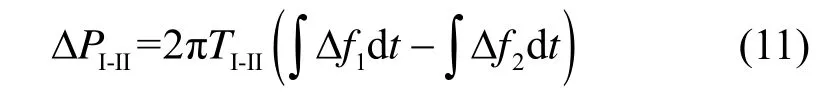
进一步对联络线交换功率增量方程进行拉普拉斯变换可得到联络线的传递函数方程N(s)为:
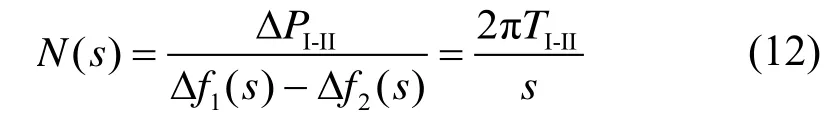
式中:Δf1和Δf2为各区域频率相对额定值的偏移量。
2 新能源渗透率对AGC系统的影响分析
2.1 新能源渗透率的定义
近年来,由于新能源并网渗透率逐年增加,电网正在向低惯性系统转变。火电机组因高比例新能源的接入需要调整其运行方式,使用不同的调峰手段来提高系统消纳新能源的能力。为简化分析,定义新能源出力渗透率为新能源发电出力与系统负荷功率的比值,其表达式为:

式中:δ为新能源出力渗透率;SNER为新能源发电出力;SL为系统负荷功率。
根据新能源出力渗透率的定义,则常规机组的发电系数可用1-δ来表示。如果新能源出力渗透率逐渐提高,那么传统发电机组的发电出力将逐渐下降,系统抵抗负荷扰动的能力也会随之降低。
2.2 启停调峰下的频率响应模型
在火电机组通过调整自身负荷来配合电网实施负荷调节的过程中,主要有启停调峰和深度调峰2 种典型的调峰运行方式。其中,启停调峰是指当新能源出力渗透率增加时,火电机组将通过关停并网机组台数来平衡系统发电盈余的过程。新能源出力渗透率增高意味着新能源机组逐渐取代系统内的火电机组数量,此时的新能源出力渗透率与系统的惯量系数成负相关。若以系统负荷功率作为基准值,随着渗透率δ不断增加,系统的转动惯量系数将会逐渐减小,可以得到表达式为:
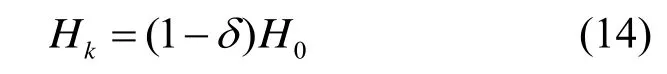
式中:Hk为新能源渗透率为δ时的电力系统惯量系数;H0为不含新能源的系统惯量常数。为简化分析,本文的新能源渗透率δ取值范围为0~40%。
同时,由于部分并网火电机组的关停,火电机组相关的控制参数也会随之变化。区域i等效调差系数Ri和等效频率偏移系数Bi在新能源出力渗透率δ的电力系统中的数值可进一步修改为[21]:

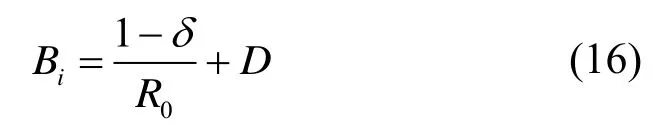
式中:R0表示不含新能源的电力系统调差系数。
在启停调峰运行方式下,新能源的引入对常规火电机组的惯量进行了修正,导致系统的惯量降低,将会显著降低电力系统的抗干扰能力。忽略新能源的调频能力,将新能源渗透率引入到常规火电机组调峰时的AGC 频率响应模型中,其频率简化分析模型如图4 所示。

图4 计及新能源渗透率的频率简化分析模型Fig.4 The simplified frequency analysis model considering permeability of new energy
2.3 深度调峰下的频率响应模型
区别于启停调峰运行,火电机组在深度调峰运行时将会保证机组不脱网运行,保留系统中的常规同步发电机数量,进而可认为电力系统的转动惯量基本不变,提高了维持系统频率稳定的能力。在实际系统中的深度调峰是指当新能源出力渗透率增加或减少时,调节火电机组的出力来适应新能源机组的出力,保证系统电量实时平衡。
火电机组在深度调峰运行时,由于没有关停常规的同步发电机组,当新能源出力渗透率变化时,系统中的其它参数如系统惯量系数、旋转阻尼系数等将不再发生变化。
新能源并网容量的扩大及电网负荷峰谷差的加大,对系统调峰电源的要求也逐渐升高。结合本文需考虑到深度调峰的情况,使用负荷率来反映火电机组调峰程度。火电机组负荷率定义为:
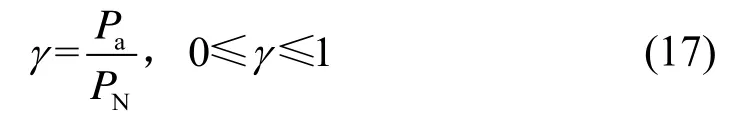
式中:γ为火电机组负荷率;Pa为火电机组实际发电出力;PN为火电机组的额定功率。
采用深度调峰方式后,火电机组的负荷率γ与新能源出力渗透率δ的关系如下:

式中:Pc为系统中等值火电机组的额定容量。
火电机组负荷率γ既受新能源消纳水平的影响,又反映出发电机组的实际运行状况,能够直观体现新能源并网对火电机组的影响[22]。鉴于火电机组处于深度调峰运行状态下的机组负荷率γ较低,本节有必要对处于不同负荷工况下火电机组的频率响应性能展开研究。
首先假设系统中只存在1 台600 MW 的火电机组,该机组在负荷率γ分别为100%、75%、50%、40%和30%的5 种工况下稳定运行,计及调速器死区限制和机组爬坡率约束这些非线性环节,建立如图5 所示的测试模型。其中,调频控制器K(s)选用经典的PI控制。测试过程中,本文采用灰狼优化(grey wolf optimizer,GWO)算法对控制器参数Kp和Ki进行寻优,保证不同负荷工况下的控制效果达到最优[23]。
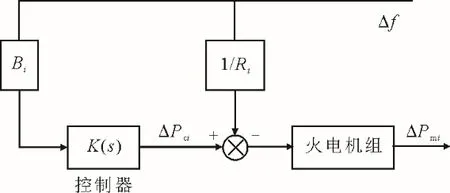
图5 不同工况下简化的机组特性测试模型Fig.5 The simplified unit characteristic test model under different working conditions
鉴于常规GWO 算法中收敛因子h是线性递减的,导致算法的全局搜索能力较弱,容易过早地陷入局部最优解。故本文对收敛因子h进行了改进,改进后的非线性收敛因子h的表达式如下[24]:
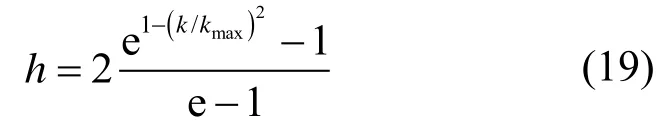
式中:e 为自然对数的底数;k为当前迭代次数;kmax为最大迭代次数。
GWO 算法对控制器参数寻优的过程可描述为:首先在参数搜索空间内随机初始化生成灰狼种群X(k);然后计算当前种群搜索个体的适应度值,通过GWO 算法对灰狼种群X(k)不断迭代更新,保证目标函数值达到最小值,此时的最优解即为灰狼首领对应的寻优向量。具体算法寻优过程如图6 所示。
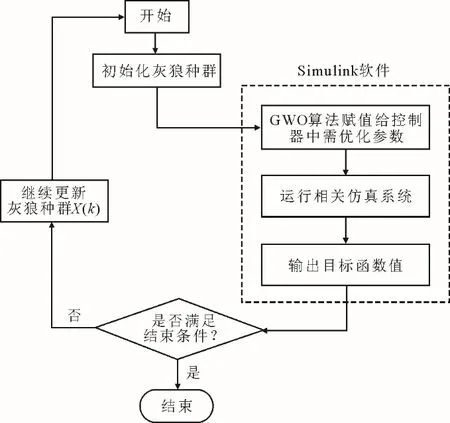
图6 GWO 算法优化控制器参数流程Fig.6 Flow chart of the controller parameter optimization using GWO algorithm
测试过程中,系统于t=10 s 时施加Δf=0.1 Hz 的频差阶跃扰动信号,得到火电机组运行在不同负荷工况下的输出功率变化量ΔPm如图7 所示。
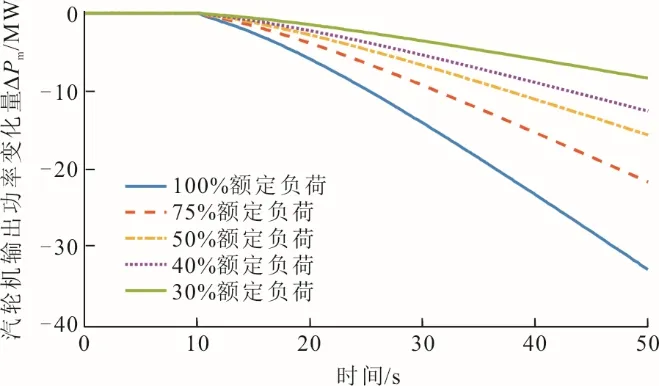
图7 单台机组不同工况下的输出功率变化量Fig.7 Variation of the output power of single unit under different working conditions
由图7 可见,当面临系统频率偏差时,处于不同负荷工况下运行的火电机组都会减少自身出力来应对系统频率偏高的情况。但是,随着机组负荷率γ的下降,系统的响应速率也在随之降低,并且火电机组输出功率的变化量在相同时间内也随着负荷工况点的降低而不断减小。验证了随着调峰深度的不断增加,火电机组的频率调节出力在逐渐减小。
3 风电参与电网调峰的频率控制策略
3.1 风电参与系统调频的控制策略
火电机组进入调峰运行时,有利于提高新能源并网消纳能力,进而促进我国能源结构转型[25]。因此本文有必要引入新能源机组,而风电机组作为主要的新能源机组,在电网调峰运行时充分挖掘风电的调频潜力,可以减轻调峰火电机组的调频压力。
由于变速风电机组并网运行时转子转速与系统频率相互解耦,当系统频率发生动态偏移时,风电机组不能影响到系统的频率响应。为保证风电高渗透率并网后电力系统频率的稳定控制,需要对风机添加相应的控制策略,使风机表现出类似于火电机组的惯量特征和一次调频特性。目前风电参与电网调频有2 种常见的控制方式,即:
1)虚拟惯量控制 考虑变速风电机组无法响应系统频率Δf的波动来对电力系统进行惯量响应,引入附加频率微分控制,以系统频率变化量为输入信号,使得风电机组输出功率与系统频率变化产生关联,来模拟惯量响应的过程。在该控制方式下,风电机组产生的附加功率ΔPw1为:
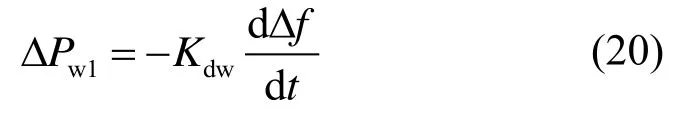
式中:Kdw为虚拟惯量控制的微分增益。
由式(20)可知,当系统频率发生动态偏移时,快速调整风机的电磁功率来平衡系统功率,使变速风电机组可以像传统机组一样给与系统惯量支撑。
2)下垂控制 为模拟火电机组的下垂特性,在风电机组中添加下垂控制环节。类比于常规火电机组的功率-频率静态特性,当系统频率Δf变化时,风电机组调节有功出力来补偿系统功率失衡。针对下垂控制,可得附加功率ΔPw2的表达式为:
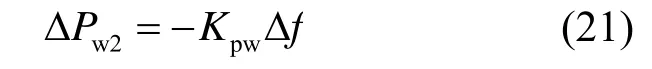
式中:Kpw为风电机组的下垂控制系数。
由式(21)可知,下垂控制通过对频率偏差起作用,利用提高有功功率降低系统的频率偏移,其有效地模拟了常规火电机组的一次调频能力。
上述控制方式在实施过程中通常需加入滤波器,滤除相应的输入信号中干扰的噪音信号。根据式(20)和式(21)可知,根据系统频率偏差,增加的风电机组辅助功率Pa为:
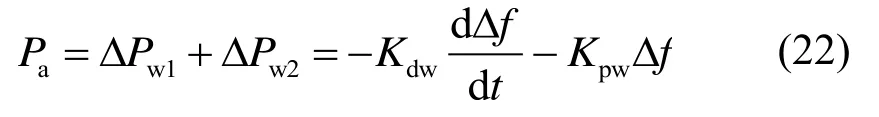
3.2 改进的综合惯性控制策略
根据上述2 种控制策略的基本原理,联合两者控制,建立综合惯性控制方式来模拟变速风电机组对系统频率变化的调节作用[26-27]。但是,传统综合惯性控制与风机MPPT 控制之间存在一些矛盾。以系统频率突降为例,在综合虚拟惯量的控制下,风机输出的电磁功率增加,若不考虑风速变化,则风机的机械功率保持不变,这就引起风力机转速ωwr降低,转速的降低导致MPPT 控制的有功参考指令Popt减小,风电机组的输出功率反而有可能下降。针对上述问题,本文引入改进的风机综合惯性控制策略,其原理如图8 所示。通过设计的转速补偿模块来补偿风机转速信号的改变,解决综合惯性控制与风机MPPT 控制之间相互干扰的问题[28]。
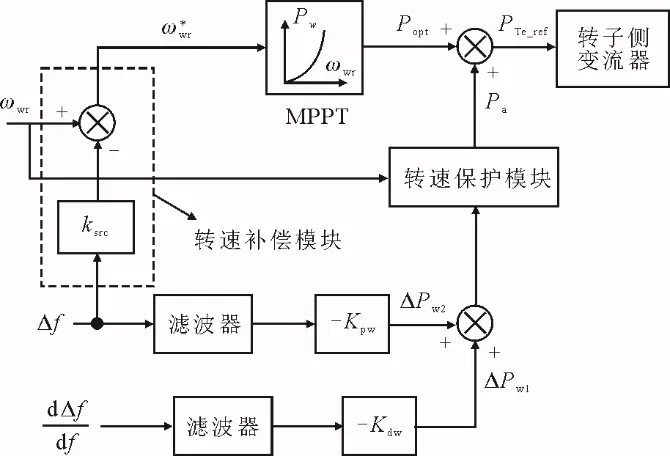
图8 改进的综合惯性控制原理Fig.8 Schematic diagram of the improved integrated inertial control
该控制策略在系统频率变化导致风机转速变化时,引入系统频率偏差信号来补偿风机转速的变化,从而补偿MPPT 控制的有功参考指令Popt。整理可得风机运行在MPPT 模式下的有功参考指令表达式为:
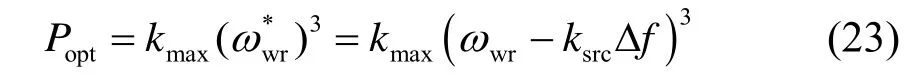
式中:kmax为最优功率曲线系数;为补偿后MPPT 控制模块的输入转速;ksrc为转速补偿系数,ksrc=Δωwr/Δf。
进一步可推导出风电机组在该控制策略下的有功功率参考指令PTe-ref为:
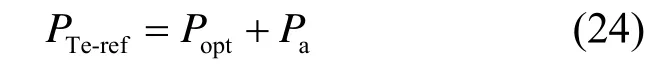
由式(24)可知,风机采用该控制策略响应系统频率的变化调节有功出力时,不但利用改进的综合惯性控制产生的辅助功率Pa为系统调频提供支撑,而且可以依据系统频率偏差信号调整风机的转速,从而对MPPT 模式下的有功参考指令做出补偿,在一定程度上减少了这2 种控制方式的相互作用,给电网调峰时应对负荷扰动的频率调节出力提供更有效的功率支撑。
4 算例
为验证前文所提控制策略应用于电网在调峰运行时频率稳定控制的有效性,本文采用图9 所示的2 区域系统进行仿真验证。

图9 改造后的4 机2 区域系统Fig.9 A modified 4-machine 2-area power system
该电网模型包含1 个等值风电场(300 台×2 MW 风电机组GW)和4 台火电机组(G1、G2、G3、G4),每台火电机组的视在功率为900 MVA,2 区域的电网负荷总容量为2 400 MW。当系统无新能源接入时,火电机组的初始参数见表1。

表1 不含新能源的电力系统初始参数Tab.1 Initial parameters of the power system without new energy
4.1 不同渗透率下电网调峰时的频率响应特性
当风电机组接入区域I时,随着风电场注入的功率不断增加,为提高风电并网的消纳水平,火电机组开始进入调峰运行状态。此时暂不考虑随机风速扰动的影响,假设风电场的风速恒为10 m/s。在恒定风速下逐步增加区域I的风电渗透率,并且系统区域I于t=10 s 时突增5%负荷,机组在不同调峰运行方式下区域I的频率响应情况如图10 和图11 所示,此时风电机组不参与系统调频。
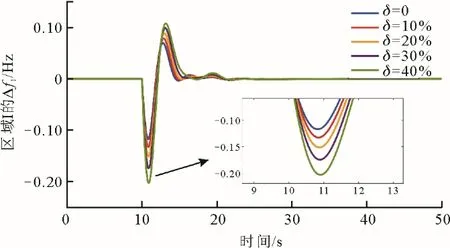
图10 不同风电渗透率下的启停调峰Fig.10 Start-stop peak shaving under at different wind power permeabilities
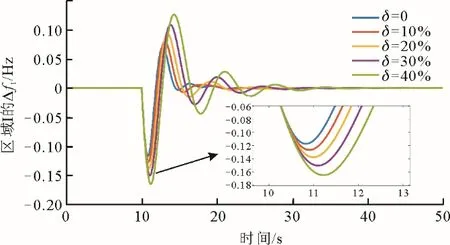
图11 不同风电渗透率下的深度调峰Fig.11 Deep peak shaving at different wind power permeabilities
由图10 可见,随着风电渗透率的不断增加,采用启停调峰运行方式的电力系统频率调节效果随之变差,其根本原因在于风电功率比重的提高是通过关停部分火电机组实现的,电力系统的转动惯量系数明显下降,使得抵抗负荷扰动的能力也逐渐下降。由图11 可见,当系统采用深度调峰运行方式时,当风电渗透率增加时,系统频率的调节效果逐渐变差,主要原因在于随着机组负荷率γ的降低,机组的频率调节出力呈下降趋势。表2 为不同风电渗透率下区域I的频率特性指标。由表2 可知,在相同的风电渗透率下,深度调峰运行方式下的系统最大频率偏差绝对值明显小于系统进行启停调峰时的最大频率偏差绝对值,并且这个差距随着风电渗透率的增加而增大。故相较于启停调峰方式,电力系统在高渗透率新能源下采用深度调峰运行方式将会在较大程度上保留系统抗负荷扰动能力,有利于电力系统维持频率稳定。

表2 不同渗透率下的最大频率偏差绝对值Tab.2 Absolute value of the maximum frequency deviation at different permeabilities
4.2 风电参与调频对电网调峰的频率影响分析
在考虑调速器死区和机组爬坡率约束的前提下[29],为验证改进的风机综合惯性控制策略对电力系统调峰运行时频率稳定控制的有效性,让并网风电机组采用不同的控制策略进行对比分析。假设风电场处于恒风速工况,在风电渗透率δ=40%下,当系统区域I施加0.05 pu 的负荷突增时,此时系统区域I的频率响应过程分别如图12—图13 所示。
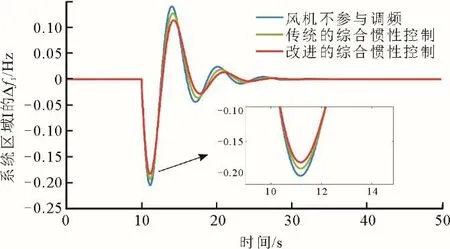
图12 恒风速下系统进行启停调峰时的频率响应曲线Fig.12 Frequency response curves of the system in startstop peak shaving at constant wind speed
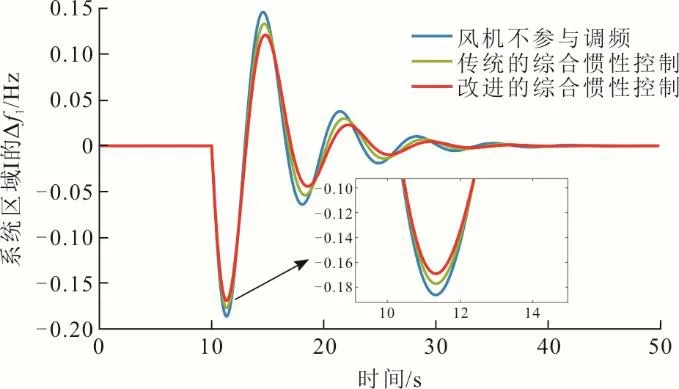
图13 恒风速下系统进行深度调峰时的频率响应曲线Fig.13 Frequency response curves of the system in deep peak shaving at constant wind speed
由图12 和图13 可见,不论系统是处于启停调峰运行还是深度调峰运行方式下,相较于传统的综合惯性控制方法,风电机组采用改进综合惯性控制策略可以更有效地提升系统频率的最低值,应对负荷突增时能提供有功支撑。由此可见,风机采用该控制策略能提高电网调峰运行时的调频能力,有助于改善系统的频率响应特性。
4.3 随机风速下电网调峰时的频率响应
设定风电渗透率δ=30%,鉴于实际风速是变化的,在风电场中进行变风速模拟,变风速模型中基本风速为10 m/s,来模拟含风电的实际系统调峰运行时的频率响应情况,风速曲线如图14 所示。
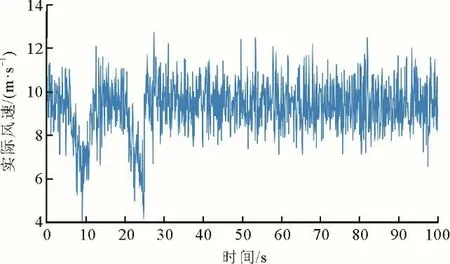
图14 实际风速曲线Fig.14 The actual wind speed curve
在变风速的情况下系统区域I于t=10 s 时突增5%负荷,分别按照风电场不参与系统调频和风电机组采用改进的综合惯性控制策略参与系统调频进行仿真,仿真结果如图15—图17 所示。
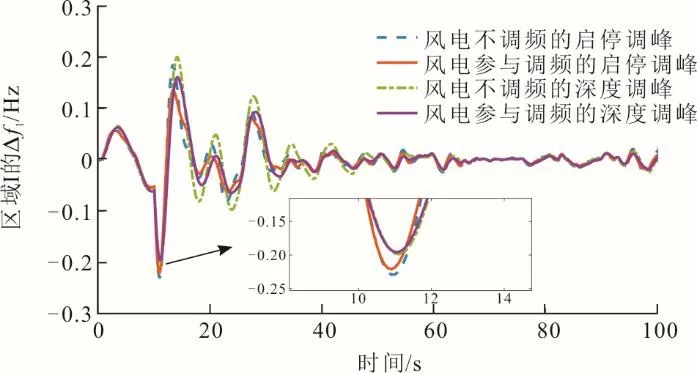
图15 变风速下系统区域I的频率偏差Δf1Fig.15 Frequency deviation Δf1 of system area I at variable wind speed
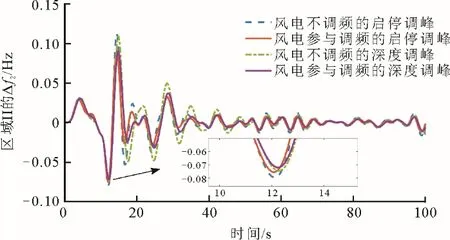
图16 变风速下系统区域II的频率偏差Δf2Fig.16 Frequency deviation Δf2 of system area II at variable wind speed
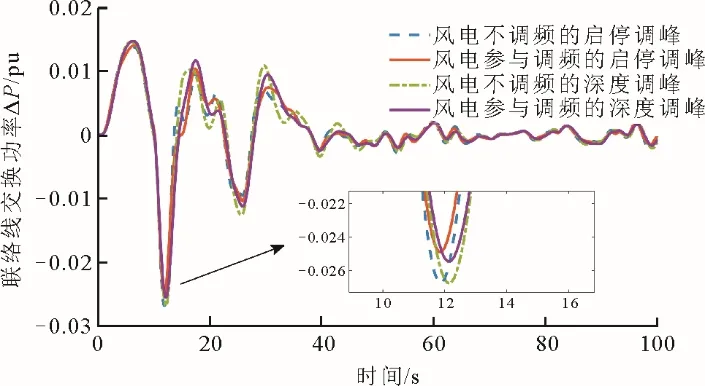
图17 变风速下系统的联络线交换功率偏差Fig.17 The exchange power deviation of tie line of the system atc variable wind speed
由图15—图17 可见,在相同的风电渗透率下,让风电机组采用改进综合惯性控制策略参与系统的频率调节,很好地改善了系统处于调峰运行时的频率调节情况。并且在高风电渗透率的情况下,系统采用深度调峰方式相比于启停调峰方式来说能够更有效地抵抗负荷扰动和应对随机风速的影响。从考虑系统频率最大偏移程度而言,电力系统采取深度调峰方式比启停调峰来说具有明显的优势。但是深度调峰会导致常规机组在低负荷时调节能力较弱,同时,深度调峰也会增加常规机组的运营成本和运营风险。所以,在实际系统中应综合考虑这2 种调峰方式,供电网管理人员进行系统运行规划。
5 结论
本文针对大规模风电并网下电力系统调峰运行时的频率稳定问题,研究了系统电源侧2 种典型的调峰运行方式对电网频率调节的影响规律,对比分析系统处于不同调峰运行方式下的频率动态响应性能,主要研究结论如下:
1)随着风电渗透率的增加,系统无论是处于启停调峰还是深度调峰运行方式下,在应对负荷扰动时,其频率调节效果都会逐渐变差,最大频率偏差绝对值随之变大。同时,系统频率波动程度在启停调峰运行时相对深度调峰运行时更大。例如,当风电渗透率δ=30%时,启停调峰的|Δfmax|为0.176 Hz,而深度调峰的|Δfmax|是0.159 Hz,且两者间的差距随着风电渗透率δ的增加而增大,由此可知,火电机组采用深度调峰方式有利于系统频率稳定。
2)针对传统综合惯性控制与风机MPPT 控制相互影响的问题,引入改进的综合惯性控制策略,在传统的惯性控制基础上增加转速补偿模块,有效地提高了风机的频率响应能力。通过仿真验证了该控制方法应用于电力系统在调峰运行时频率稳定控制的有效性。
3)通过对单台火电机组在不同负荷工况下的输出功率和响应速度进行仿真分析可以得出,随着机组负荷率的降低,火电机组的频率调节出力也在逐渐减小。为解决电网调峰运行时应对负荷扰动的频率稳定问题,火电机组采用深度调峰方式,结合改进的风机综合惯性控制策略,有效地改善了电网调峰运行时的频率调节效果。
