基于速度预测的锻造操作机大车定位控制研究

2022-10-17刘晨荣魏海涛张晓丽王宏亮

液压与气动 2022年10期

刘晨荣，魏海涛，张晓丽，王宏亮

(兰州兰石集团有限公司能源装备研究院，甘肃兰州 730314)

引言

锻造操作机作为快锻液压机组的关键组成之一，其性能指标直接影响液压机组的生产效率及产品品质。锻造操作机行走性能是衡量其性能的关键指标之一，行走液压系统作为典型的阀控马达系统，其负载惯量大，响应速度慢，平稳精准控制较为困难[1-5]。同时在其停车阶段存在较大液压冲击[6-8]、停车振荡等问题，降低了定位精度及停车速度，加速液压、机械元件损坏。为了改善操作机行走性能，国内外学者针对其液压系统设计及控制方法策略进行了广泛研究[9-13]。

本研究针对锻造操作机停车控制精度及振荡优化，结合乔志刚等[14]提出的快锻压机速度-位置复合控制思想及顾临怡等[4]研究成果，提出了基于速度预测的锻造操作机定位控制方法，本研究以某5 t锻造操作机为例，搭建其机械系统ADAMS模型、液压系统AMESim模型，基于联合仿真验证了基于速度预测的定位控制方法的有效性。

1 虚拟仿真模型搭建及参数校准

锻造操作机行走机械系统ADAMS仿真模型如图1，行走液压系统AMESim仿真模型如图2所示，表1中列出了液压系统关键元件参数。本研究中，AMESim模型中输出量为减速机输出扭矩T，输入量为马达角速度ω、操作机速度v、位移s；在ADAMS中选择驱动齿轮的角速度ω、位移s和速度v作为输出，输入驱动齿轮的扭矩T。

图1 行走机械系统ADAMS仿真模型

1.液压泵 2.电机 3.溢流阀 4.先导换向阀 5.单向阀 6.比例换向阀 7-10.单向阀 11.溢流阀 12、13.马达 14.减速机 15.转换接口 16.ADAMS接口 17-20.软管

表1 行走液压系统关键参数设置

为了仿真模型准确可行，以实测液压阀控制信号为输入，对比仿真输出与实测的马达进、出油口压力曲线、锻造操作机位移曲线，调节机械系统、液压系统参数设置，最终结果如图3所示，仿真精度较高，联合仿真模型能够较好的反映实际系统。

如图3所示，在t=4.98 s时，比例阀全开，马达进油口压力瞬时升高至10 MPa；t=14 s时，比例阀开始关闭，由于大车惯性，马达出油口压力上升，进油口压力下降，马达开始反向制动；当出油口压力达到最大，大车速度降为0 m/s，但此时，由于马达出油口压力大于进油口压力，反向扭矩达到最大且大于操作机机械系统摩擦力，操作机在马达反向扭矩作用下开始反向加速，马达进油口压力上升，出油口压力下降；当马达进油口与出油口压力差达到最大时，大车开始正向加速，如此反复振荡运行，直至马达扭矩不足以克服系统摩擦时大车才稳定停车。

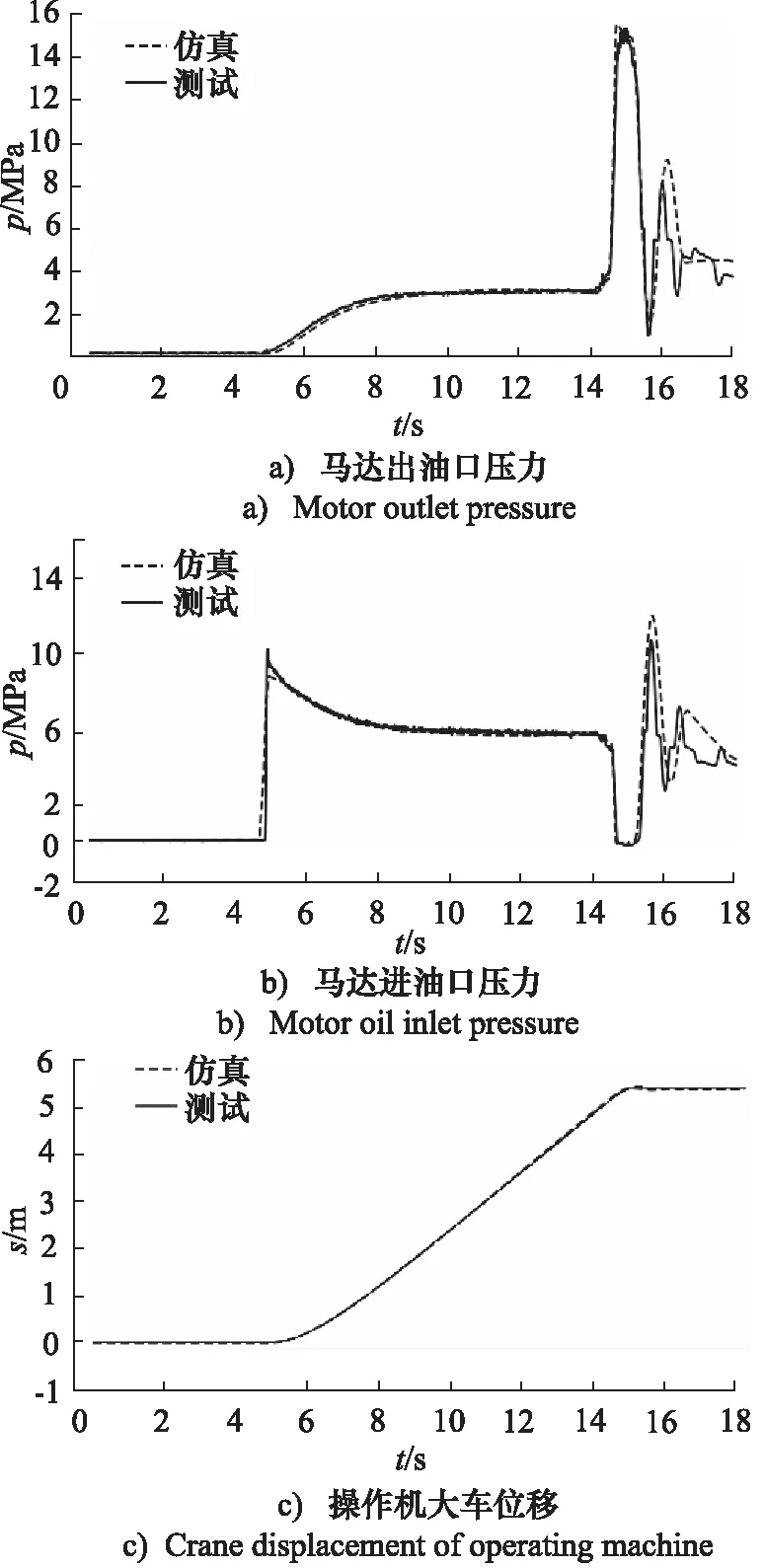
图3 仿真与测试对比曲线

综上，大车停车振荡问题主要由于马达反向驱动扭矩引起，具体表现为大车停车速度为0时，液压系统没有及时卸压。

2 停车振荡优化

操作机液压行走系统为典型的阀控马达系统，在实际控制中，依据经验提前分段减小比例阀开度，达到停车控制目的；但其停车距离长，停车精度低通常为±(5～10) mm，且容易造成停车振荡问题。典型的比例换向阀控制操作机停车过程，如图4所示。停车过程存在明显的振荡，约在15.1 s时，大车速度降为0 m/s，而此时马达出油口压力达到最大，进油口压力最低，马达反向驱动扭矩达到了最大。

图4 比例换向阀控制制动过程

操作机停车控制核心问题为马达出口压力控制，文献[4]中提出基于可控节流阀来控制马达出口压力，大惯量负载可平稳停车，在此不再赘述。

2.1 比例溢流阀制动控制

为了消除或减小停车振荡，在制动过程中大车速度降为0时，马达进、出油口压力差要尽可能的小，从而使马达驱动力远小于机械系统阻力，进而实现稳定快速停车。为达到这一目的，需要在速度低于某个速度时，控制马达出油口压力随着操作机速度的下降，让其接近于马达进油口压力。因此，可采用速度反馈比例控制电磁溢流阀，来达到平稳无振荡停车。

采用速度反馈比例控制溢流阀控制停车制动过程，如图5所示。为了分析比例溢流阀控制效果，仿真中比例换向阀在第4秒瞬时关闭，马达出油口压力达到上升至最大，进油口压力降低，马达开始反向制动，经0.5 s操作机速度降为0.092 m/s，开始主动控制马达出油口压力，经0.1 s后马达进、出油口压力分别为1 MPa，1.09 MPa(系统初始压力1 MPa)，速度平稳降为0，由此可见，采用速度反比例控制可以实现快速平稳无振荡停车。

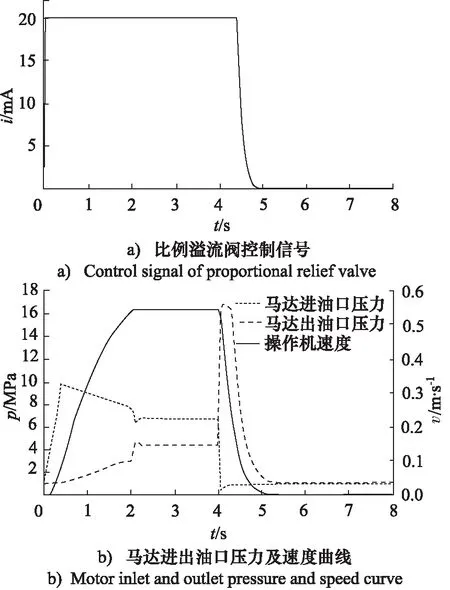
图5 比例溢流阀制动过程

2.2 速度反馈比例增益确定

综上论述，在制动阶段比例溢流阀控制信号可表示为：

Sf=|v|×g

(1)

式中，v—— 操作机行走速度

g—— 反馈控制比例增益

Sf—— 比例溢流阀控制信号

为了避免输入信号过大而损坏比例溢流阀电器元件，需要对Sf幅值进行限制：当Sf>Smax时，Sf=Smax，Smax为比例溢流阀电器元件允许最大值输入。

增益g越小，制动距离越大，随着g值增大，制动距离减小，当g值大于临界值glim时系统开始出现停车振荡。临界值glim可以通过试验测试或仿真等得到估计值。

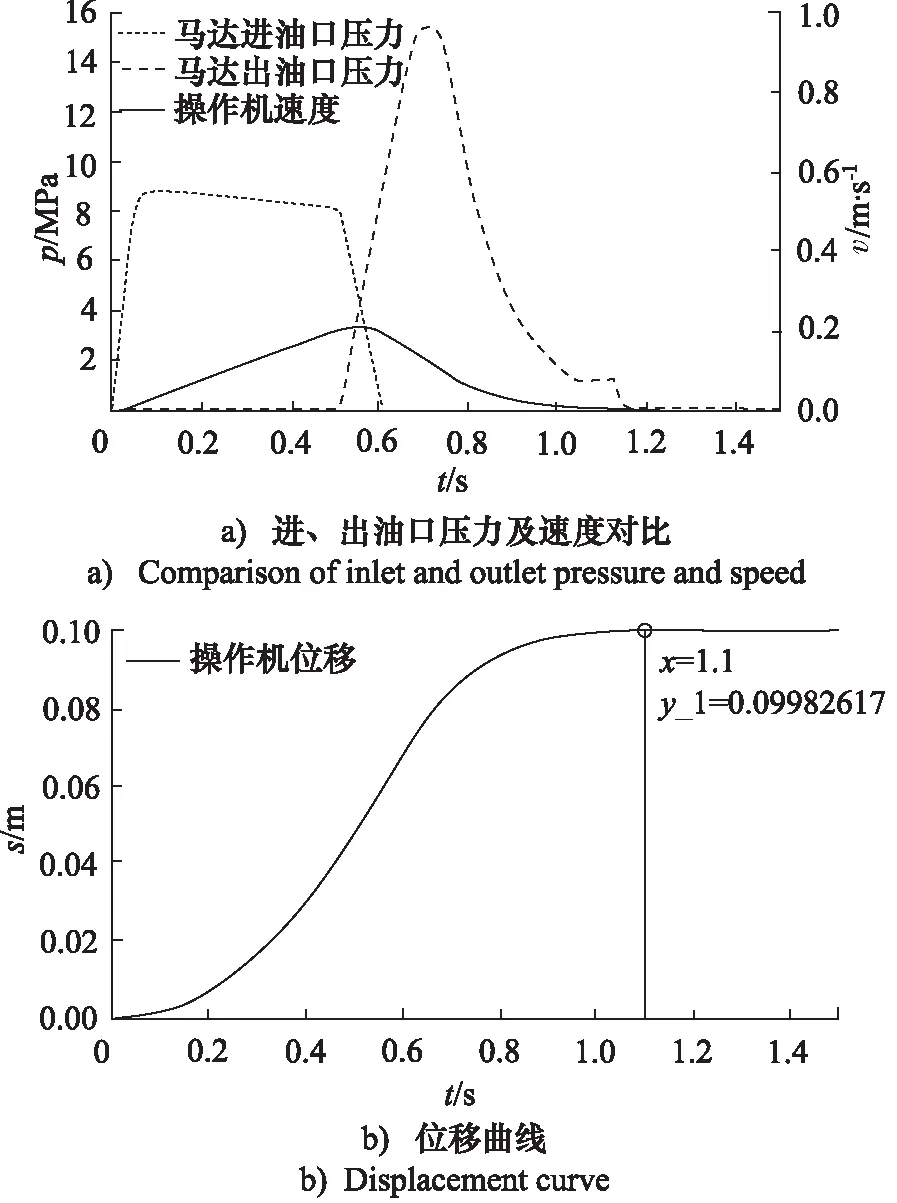
图6为不同g值时停车点附近局部曲线。当g>0.6时，出现停车振荡；当0.4

图6 不同增益g值停车位移局部曲线

经仿真分析，当g大于Smax/(vmax/10)时，停车距离随g值的变化较小，本研究中g的最大值取：

gmax=Smax/(vmax/10)

(2)

为了避免停车距离过长，反馈控制比例系数g不易过小，本研究中g的最小值取：

gmin=Smax/(3×vmax/10)

(3)

3 速度预测+补偿定位控制

锻造操作机行走速度越大，其系统动能越大，制动距离越长。系统制动过程中动能主要由液压马达反向制动消耗。不考虑油液温度和系统泄漏影响，根据锻造操作机液压系统设计，制动过程中主要由溢流阀控制马达制动压力，当溢流阀溢流压力不变时，操作机制动距离仅与开始制动瞬时速度有关。

3.1 制动距离预测

为了避免停车振荡，本研究在引入停车振荡优化基础上(g≈(gmax+gmin)/3)，根据速度预测制动距离。由于操作机制动过程涉及机械系统、液压系统，直接采用数学描述较为困难，利用联合仿真手段可以有效简化分析过程。利用建立的仿真模型，得到不同制动瞬时速度下制动距离。经大量仿真分析验证，制动瞬时速度与制动距离满足二次函数关系，如式(4)所示。

(4)

式中，ss—— 制动距离

vc—— 开始制动瞬时(比例阀完全关闭瞬时)操作机行走速度

a，b，c—— 由系统特性确定的常数

3.2 速度预测+比例系数补偿定位控制

由于控制周期不可能无限小，开始制动瞬时，操作机当前位移距离目标位移值与预测制动距离值存在差值，差值在[-vmaxT，vmaxT]范围内波动，此差值最终表现为系统定位误差。

在制动距离预测分析中，引入停车振荡优化，比例控制系数g为定值，难以消除或减小定位误差。由于制动瞬时目标距离差无法改变，只能通过调整比例控制系数g在制动距离ss补偿一个变化量Δs，以减小制动瞬时目标距离差与预测制动距离差值，减小定位误差。在此引入比例控制系数g修正系数λ来调整制动距离变化量Δs。

经大量仿真测试分析，比例控制增益g一定时，修正系数λ与Δs的满足：

(5)

经修正，反馈控制增益G为：

G=g*λ

(6)

3.3 控制流程

速度预测+补偿定位控制流程如下：

(1) 给定位移值s；

(2) 根据位移反馈sb，计算距离差sd=s-sb；

(3) 根据速度反馈vb，由式(4)，计算预测制动距离sp；

(5) 计算比例增益修正系数λ，由式(5)给出；

(6) 制动状态完全关闭比例换向阀，并主动控制比例溢流阀，比例阀控制信号由式(6)计算；

(7) 检测速度反馈vb是否为0，若vb=0，则本次定位控制过程结束，若vb≠0，则返回步骤(5)。

4 仿真验证

以经校准的机械ADAMS模型、AMESim模型为控制对象，编写控制程序，进行仿真验证。

反馈控制比例增益g=0.2，根据测试，停车距离速度预测函数为：

ss=0.000496v2+0.05787v+14.05

(7)

修正系数λ计算公式为：

(8)

目标位移为0.1 m时，操作机速度与马达进、出油口压力对比曲线，如图7所示。

从图7a中可以看出，当行程为0.1 m小行程时，在速度为0.2 m/s时(未达到最大速度)，操作机开始制动。从图7b中可以看出，最终停车位移为0.09983 m，停车定位误差为0.17×10-3m，制动过程无振荡。

图7 行程1 m的制动过程

目标位移为1.497 m时，操作机速度与马达进、出油口压力对比曲线，如图8所示。

从图8a中可以看出，当行程为1.497 m大行程时，经过1.9 s，操作机速度达到最大，此时操作机位移(sb=0.6 m)距离目标位移(s=1.479 m)为sd=0.69884 m，预测制动距离sp=0.19589 m， Δs=|Ds-ps|= 0.6831 m，大于0.55 m/s×0.01 s= 5.5×10-3m，操作机以最大速度继续前行。在3.18 s时，操作机位移(sb=1.30535 m)距离目标位移(s=1.497 m)为sd=0.1917 m。Δs=4.2×10-3m小于5.5×10-3m，操作机开始制动。若比例控制增益修正系数λ=1即未修正，则最终定位误差为4.2 mm。如图8b，根据式(8)增益修正系数λ=0.1511，最终停车位移为1.49724 m，停车定位误差为0.24×10-3m，表明比例增益修正系统对于减速系统定位误差是有效的。